高中數學教材“推廣型”內容的教學策略

曾榮

數學推廣是指在一定范圍內或一定層次上對數學概念、定理、法則進行拓展，使之在更大范圍或更高層次上成立，它是數學研究不可或缺的基本方法[1]。在高中數學教材中，設置了大量的“推廣型”教學內容，如：將0°～360°角推廣到任意角，將銳角三角函數推廣到任意角的三角函數，將勾股定理推廣到余弦定理，將平面幾何中的向量方法推廣到立體幾何中的向量方法，等等。教師如能結合這些內容的教學，讓學生經歷推廣的過程，體驗數學在結構上的和諧性，并嘗試通過類比、歸納、化歸等思想方法解決在推廣過程中遇到的困難和問題，必然對培養學生的創新思維具有重要意義。

一、“推廣型”內容教學時需解決的問題

1.推廣的必要性

解決推廣的必要性問題，即要解決“為什么需要推廣？”這一問題。教學中應從學生已有的認知水平出發，結合數學發展的現實基礎和邏輯基礎，讓學生深刻領悟到進行推廣的必要。例如，在引入大于360°的角和負角時，可以舉些學生熟悉的生活中大于360°的角和負角，如體操中的轉體、跳水中的翻騰、鐘表中的指針、自行車的輪子、螺絲扳手與曲柄連桿等按不同方向旋轉時所成的角，用以說明建立新概念的必要性和實際意義，這也有利于體驗數學的人文價值，開闊學生的視野。

2.推廣的方法性

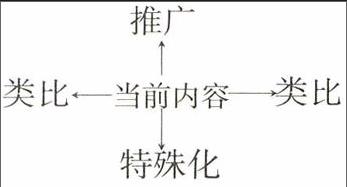
解決推廣的方法性問題，即要解決“如何進行推廣？”這一問題。從數學學習、研究過程來看，經常使用如下的邏輯思考方法：

其中突出顯示了聯系的觀點，通過類比、推廣、特殊化、化歸等思想方法，可以極大地促進學生的數學思考，使他們更有效地尋找出自己感興趣的問題，從中獲得研究方法的啟示。例如，關于平面幾何中的向量方法，我們可以有如下的“聯系圖”：

3.推廣的應用性

解決推廣的應用性問題，即要解決“推廣后有什么用？”這一問題。在聯系舊知推廣得到新知的基礎上，要重視新知的應用，讓推廣的價值得到充分的展示。這種價值，不僅體現在新知對舊知的覆蓋，更要讓學生感受到一個數學概念的推廣可能帶來很多更好的性質。例如，將勾股定理推廣到余弦定理以后，可以講解這樣的問題：用余弦定理證明：在△ABC中，當∠C為銳角時，a2+b2>c2;當∠C為鈍角時，a2+b2

二、“推廣型”內容的教學基本策略

1.創設具有認知沖突的問題情境，揭示推廣的必要性

認知心理學家認為：當學習者發現不能用頭腦中已有的知識來解釋一個新問題，或發現新知識與頭腦中已有的知識相悖時，就會產生“認知失衡”。這種認知沖突會讓學生產生新奇和驚愕，從而引起學生的注意、關心和探究。認知沖突是教學和學習的最佳契機。在進行“推廣型”教學內容的教學時，創設具有認知沖突的問題情境，將有利于推廣必要性的揭示。

（1）情境生活化，使推廣成為需要。解決現實生活和生產實際問題的需要，常常是進行數學推廣最直接、最有力的推手。為此我們可以結合具體的實例創設情境，使新知自然生成。例如，我們將0°～360°角推廣到任意角時，可創設如下問題情境。

案例1 ?角的概念的推廣的問題情境

問題1 在初中我們是怎樣定義角的？（從如下的靜態和動態兩個角度定義。）

問題2 ?平面內一條射線繞其端點旋轉一周后回到原來的位置，所形成的角是什么角？如果繼續旋轉下去，所形成的圖形還是不是角？為什么？

問題3 ?生活中存在剛才問題中所出現的角嗎？你能試著舉出一些實例嗎？我們又如何去理解它們呢？

通過回顧舊知，聯系生活實際，引發認知沖突，角的推廣也就成了必然需求。

（2）關系普遍化，使推廣成為必要。推廣常用的方式是將變量之間、對象之間的特殊關系改為一般關系而獲得具有普遍意義的命題及公式，或是將具體對象改為一般對象從而使命題得到推廣[2]。教學時，一般先復習包容性小、抽象概括程度低的概念，并在此基礎上創設具有認知沖突的問題情境。例如，將銳角三角函數推廣到任意角的三角函數的學習，從認知結構發展的角度來說，是屬于“下、上位關系學習”，“先行組織者”是銳角三角函數的概念[3]。教學時，可創設如下問題情境。

案例2 ?任意角的三角函數的問題情境

問題1 ?你能回憶一下銳角三角函數的定義嗎？

問題2 ?你能用直角坐標系中角的終邊上的點的坐標來表示銳角三角函數嗎？如果按這種方式用坐標表示的三角函數值，在銳角取值范圍內和之前的定義吻合嗎？

問題3 ?改變終邊上的點的位置，這三個比值會改變嗎？為什么？（在定義任意角的三角函數之前，必須讓學生感知、確認、理解這三個比值都只與角的大小有關，而與點在終邊上的位置無關，因此它們都是以角為自變量的函數，從而給出任意角的三角函數的定義。）

問題4 ?角的范圍已經推廣到了任意角，那么，仿照以上銳角三角函數的新的定義方式，你認為如何定義任意角三角函數比較合理？

通過以上問題串，由特殊到一般，思維流暢，層層深入，新概念的得出水到渠成。

2.遷移已有的思想方法，凸顯推廣的方法性

新課標強調“四基”，即學生通過學習，獲得必需的基本知識、基本技能、基本思想方法、基本活動經驗。基本思想方法、活動經驗的獲得，不僅來源于自己平時對知識的感悟，更多的來源于平時教師對思想方法的提煉、滲透。學會推廣實際上就是學會方法。教師在進行“推廣型”教學內容的教學時，應注意遷移已有的思想方法，如類比探究、化歸論證等，讓學生在推廣的過程中感悟方法、掌握方法。

（1）類比探究。類比法通過比較兩個對象的部分相同或相似，推出其他方面也可能相同或相似。類比是進行數學再發現的有效方式。在進行角的概念推廣的教學時，為了引出正角、負角和零角的概念，我們可設置如下類比式問題串。

案例3 ?類比正數、負數、零的概念，得出正角、負角、零角的概念

問題1 ?如何用數學的方法將按順指針、逆時針兩種不同的方向旋轉的角加以區分？你以前有過類似的經驗嗎？

問題2 ?我們知道，正負數和0可借助數軸有效地進行區分。那么，為了區分按順指針、逆時針兩種不同的方向旋轉的角，你認為可以利用什么載體進行區分呢？如何給它們下一個合理的定義呢？

通過以上問題，利用類比的方法，由正數、負數、零的概念自然引出正角、負角、零角的概念，同時也讓學生體驗從低維問題向高維問題發展的一般方法。

（2）化歸論證。一般化是數學推廣的基本方式。數學家G·波利亞指出：”一般化是從對象的一個給定集合進而考慮到包含這個集合的更大集合。”由下位公式向上位公式推廣時常伴隨著猜想，而要對這種猜想進行論證，則常需將上位公式化歸至下位公式。例如，我們在將勾股定理推廣到余弦定理時，可按如下方式進行。

案例4 ?借助化歸的思想論證余弦定理

問題1 ?前面學過的正弦定理的表達式是怎樣的？它具有怎樣的功能？

問題2 ?在我們所學知識中，有沒有涉及已知三角形的兩邊及夾角，求第三邊的情形呢？能否舉一個具體的例子？

問題3在△ABC中，已知邊a，b，∠C≠90°，是否還能用勾股定理求邊c？（很自然的想法是構造直角三角形，以便用勾股定理進行計算。輔助線如下圖，過程略。）

3.運用推廣的結論方法，強化推廣的應用性

舊知推廣為新知以后，內涵發生了改變，伴隨產生了一些新的性質。為了讓學生鞏固新知，體驗數學的實用價值，我們應在推廣之后，在概念的辨析、性質的應用等方面及時加以應用。

（1）概念辨析，厘清疑點。數學概念在得到推廣以后，其內涵發生了改變，容易與原有的概念產生混淆。為了幫助學生區分新舊概念的區別，加深理解，我們可以通過概念辨析題的方式進行新知的應用。如，將角推廣到任意角以后，伴隨著產生了象限角、軸線角等概念。這些概念與原有的銳角等概念容易混淆，為此我們可通過如下判斷題進行辨析。

案例5 ?角的概念推廣后設置的概念辨析題

判斷下列說法是否正確：

①銳角是第一象限角。（對）

②第一象限的角都是銳角。（錯）

③小于90°的角都是銳角。（錯）

④第二象限的角一定比第一象限的角大。（錯）

⑤終邊相同的角一定相等。（錯）

⑥終邊相同的角有無數多個，它們相差360°的整數倍。（對）

（2）前后呼應，變式應用。在問題情境的創設過程中，常借助認知沖突，設置懸念，引發推廣。在推廣以后，要及時解決原先的疑問，并適當深入，變式提升。例如，前面為了將勾股定理推廣到余弦定理，設計了這樣的問題：已知三角形的兩邊及夾角，如何求第三邊呢？那么，我們可結合此問題的解決，設計例題及變式。

案例6 ?將勾股定理推廣到余弦定理后設置的例題及變式

①在△ABC中，已知邊b=3，c=1，∠A=60°，求邊a。

②在△ABC中，已知邊a=4，b=5，c=6，求∠A。

變式1在△ABC中，已知邊a=4，b=5，c=6，判定在△ABC的形狀。

變式2在△ABC中，已知邊a∶b∶c=3∶4∶5，判定在△ABC的形狀。

知識、能力與學習品質的提升是學生發展的基本目標。通過“推廣型”教學內容的教學，讓學生充分認識推廣的必要性、方法行、應用性，在推廣中進行再發現，學會探究，對學生良好數學素養的提升具有較大的幫助。

參考文獻

[1] 徐彥輝.數學推廣及其常見形式舉例分析[J].數學通報，2010（4）.

[2] 孫世華.數學推廣的基本模式[J].數學通訊，2005（1）.

[3] 陶維林.任意角的三角函數的設計與反思[J].中國數學教育，2009（4）.【責任編輯 ?郭振玲】