由一則數學教學片斷看教材的“微創”功效

摘 ? 要?教師在進行教學時，要教得好，使學生受益，絕不能“照本宣科”，而應認真做好教材的“二次開發”。本文對教材的引入部分作了再創造，這對整節課而言，只能算是“微創”，但畫龍點睛，讓原本靜止的教材“動”了起來，讓相對無趣的課堂“活”了起來，起到了較好的教學功效。

關鍵詞?教學片斷 ?教材 ?微創 ?功效

著名教育家葉圣陶先生曾說過：“教材只能作為教課的依據，要教得好，使學生受益，還得靠老師的善于運用。”因此，教材僅僅只是提供了最基本的資源，但并不是唯一的資源，教師不能只成為課程實施的執行者，應該成為課程的建設者。而在使用教材的實際過程中，大部分教師沒有精力、也不可能對教材作較大幅度的“二次開發”，如果能對前后章、前后節的教學順序或內容作適當調整，或對某一章的某一塊內容或某一環節進行適當增刪，已經很不容易，這相當于對教材內容“微創”，意為“微小的再創造”。

“微創”是一個技術名詞，來源于醫學，就是在手術治療過程中只對患者造成微小創傷、術后只留下微小創口的技術，是相對傳統手術的科技成果。本文中的“微創”區別于醫學中的“微創”，它不是治理教材，而是立足教材，在教學過程中依據課程標準對教材內容進行“微小而適度”的加工，如：調整、增加或刪減等，使之更好地適應具體的教育教學情景和學生的學習需求。教學實踐證明，相對于傳統的“教教材”做法，“微創”不僅容易實施，而且只要“微創”得法，其起到的教學功效絕不微小。

一、案例分析

在一次初中骨干教師“送教下鄉”教學活動中，筆者設計了一節示范課《二次根式的乘除（1）》，基于創造性使用教材的理念，對教材的引入部分作了“再創造”，這對整節課而言，只能算是“微創”，但畫龍點睛，讓原本靜止的教材“動”了起來，讓相對無趣的課堂“活”了起來。

1.教材的引入部分

本節課的教材內容取自于“蘇教版數學八年級下冊第十二章二次根式”，該節教材的引入部分呈現了如下情境。

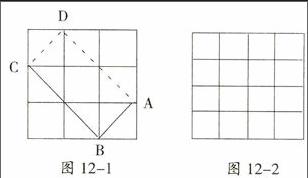
數學實驗室：（1）在圖12-1中，小正方形的邊長為1。AB=■，BC=■，畫出矩形ABCD。矩形ABCD的面積是多少？

解答：矩形ABCD的面積=■×■，又矩形ABCD的面積是4，所以■×■=4。

（2）在圖12-2中，小正方形的邊長為1。畫出矩形EFGH，使EF=■，FG=■。矩形EFGH的面積是多少？

2.微創教材

（1）變“無”為“有”

數學教學活動必須建立在學生的認知發展水平和已有的知識經驗基礎上。基于這一點，筆者通過微創教材，讓學生在教學的引入環節經歷了以下三個過程。

①回顧舊知，點睛破題。先請學生回顧、例舉二次根式，并從中選了兩個二次根式■和■寫在黑板上;再請學生回憶如何作出長為■和■的線段;然后通過在■和■之間增加運算符號“×”，自然地引出本課的學習內容“二次根式的乘除”中的乘法運算。

②應用舊知，數形結合。先請學生用原有知識解答這兩個二次根式相乘的式子，當學生無從下手時，教師提問：“剛才，我們可以利用圖形得到■，那么，這里是否也能利用圖形解決這個問題呢？”由此引導學生棄“數”從“形”，往圖形方面考慮解決的方法，想到構造長為■、寬為■的矩形，通過求矩形的面積來解答■×■。在學生畫矩形有困難時，可提示學生在網格圖中畫，從而輕松畫出。至此，具備教材上提供的所有條件，問題得到解決。

③總結方法，需學新知。筆者和學生一起歸納總結：當遇到代數問題，從“數”的角度難以求解時，可考慮轉換思路，從“形”的角度求解;反之，當遇到幾何問題，從“形”的角度難以求解時，也可考慮轉換思路，從“數”的角度求解。雖然■×■能從“形”的角度求解，方法也頗具創造性，但畢竟有些繁，而且思維量較大，因此還是希望能從“數”的角度求解，但原有知識又無法解決，這就需要學習新的知識“二次根式的乘除法”。

以上這些教學片段在教材上均沒有呈現，筆者通過創設這些過程，不僅大大激發了學生的探究欲望，培養了學生的探究能力，也讓學生充分認識到新知學習的重要性和必要性。

（2）變“有”為“無”

教材上給出的問題情境中，既有矩形，也有網格，是一個讓學生很容易解答的情境問題。在實際教學中，筆者去掉了矩形和網格，變“有”為“無”，變“直接解答”為“開放設問”，變學生解題教學為師生對話教學，讓學生經歷了自主探索的學習過程，享受了“數形結合”的思想方法滲透和應用的過程，體驗了搭建腳手架（構建網格）的過程，感悟了新知是為需所學的過程，學生的學習興趣和思維量大大增加，他們的問題解決能力和創新意識得到了有效培養。

3.微創的理論依據

（1）教學法依據

教師是教材的開發者，教師要根據學生的特點、教材的內容、教學的目標，對教材實施“微創”。在本案例中，從初二學生的特點來看，他們對新事物充滿好奇心，對教學內容不滿足于教師的單向灌輸，而有探究的欲望;從教材的內容來看，有二度開發的可能，教師可以將教學內容的引導性功能開發成為探究性功能;從教學的目標來看，教師不僅要讓學生學到知識，更要讓學生體會知識背后的數學思想方法，讓學生經歷數學探究，體驗數學研究的過程。

（2）心理學依據

建構主義心理學認為，知識是在學生的學習活動與過程中，通過與外界進行信息的雙向流動主動建構形成的，外界要通過創造合適的活動，幫助外部信息向學生內部流動，在學生將外部信息內化為自身內部的知識時，需要結合自己已有的知識經驗進行加工，這種加工得到的知識可能是合理的、正確的，但對外部刺激的反應也可能是不合理、不正確的，教師的作用就是通過設計合理的教學活動，引導學生對外部信息進行正確的加工。而本案例對教材的“微創”，是建立在學生已有的知識經驗之上，顯然是一種對學生思維合理的引導，有利于學生建構出新的知識。

二、微創功效

1.激發興趣，提升教學品味

《課標》（2011版）指出：“學生的數學學習內容應當是現實的，有趣的，富有挑戰性的。”本課的引入，如果對教材不進行“微創”，而是根據原有的材料平鋪直敘，那么這樣的學習內容對學生來說毫無挑戰性，他們也就不會產生興趣，學習由此進入被動狀態，學習效果必定事倍功半。本課通過“微創”，滿足了學生的探究欲望，充分發揮了學生的主動性和積極性，極大地激發了學生的學習興趣，使學生處于主動探究的狀態。在探究中，學生不僅掌握了數學知識本身，對數學學習的過程有了更為充分的體驗，這樣的學習才是有數學味道的數學學習，這樣的教學，也才是有數學品味的教學。

2.構建平臺，培養創新思維

數學是思維的體操，促進學生思維的發展是數學課堂教學的靈魂。在數學教學中，教師要千方百計地為學生創設促進思維的情境，構建一個互動的平臺，使數學教育真正面向全體學生，充分發揮數學在提高人的推理能力、抽象能力、想像力和創造力等方面的獨特作用。本課的引入，如果按照教材照本宣科，學生就是純粹地解兩道題，而這兩道題目對絕大部分學生而言都會做，學生的創新思維則無從培養。而現在通過“微創”教材，去掉矩形和網格，讓學生直接計算■×■，這個問題用原有的代數知識顯然無法解答，對學生而言，一般不會考慮從“形”的角度來解決，構造“形”后一般又不會想到搭建“網格”，由此就為學生構建了需要創造“矩形和網格”的思維平臺。而在課初，通過復習“如何作出長為■和■的線段”，為學生后面的“借形解數”作出了鋪墊，使教學過程顯得自然而流暢，學生的創新意識得到了培養，思維視角得到了拓寬，思考能力得到了提升。

3.倡導對話，追求開放教學

《課標》（2011版）指出：“數學教學是數學活動的教學，是師生、學生之間交往互動與共同發展的過程。”對學生而言，對話意味著心態的開放，主體性的凸顯，創造性的解放;對教師而言，對話意味著上課不僅傳授知識，而且分享理解，意味著教師角色將由主角轉向平等中的合作者，從知識的傳授者轉向學生發展的引路人;對教學而言，對話意味著參與，即學生、教材、教師之間進行一次次真情的交流。本課的引入環節通過“微創”后，為學生拋出了一個又一個“開放式、探究性”的問題，這些問題為學生提供了“想說、敢說、能說”的活性狀態下的對話機會，營造了師生和諧、熱烈的課堂合作、交流和分享氛圍，為后續的新知學習起到了良好的開端作用，真正體現出學習的本原意義。

4.立意育人，滲透思想方法

《課標》（2011版）指出：“數學思想蘊含在數學知識形成、發展和應用的過程中，是數學知識和方法在更高層次上的抽象與概括，好的數學教學，是把數學知識、方法、思維和思想融為一體的教學。”因此，數學教學的立意要高，要建立在培養學生數學素養之上，要重視對學生研究性學習能力的培養，要重視數學思想方法的滲透和應用。本課的引入通過“微創”后，有效地滲透了“形解數、數解形、數形結合”的數學思想，應用了搭建“腳手架（構建網格）”的數學方法，較好地體現了“人人都能獲得良好的數學教育”這一“以人為本”的數學課程核心理念。

5.經歷過程，才知為需而學

在數學教學的過程中，教師要精心設計必要的數學活動，引導學生通過觀察、實驗、猜測、推理、交流與反思，以已有的知識和經驗為基礎進行積極、和諧的建構，讓學生親身經歷和感悟知識、技能的形成與鞏固過程，經歷數學思維的發展過程，體驗問題的結論和方法之間的精彩過程，從而把新的學習內容正確地納入到已有的認知結構中，進而形成積極的數學情感與態度，自覺主動地獲取新的數學知識。本課的引入通過“微創”，讓學生參與數學知識的發生、發展過程，了解新知產生的由來，既有利于學生掌握和理解知識，也有利于學生真正理解和體會到新知是為了比較方便地計算“二次根式的乘法”的需要而學習，從而激發學生內在的學習動力。

6.立足效率，落實課程目標

《課標》（2011版）指出，“教學活動是師生積極參與、交往互動、共同發展的過程。有效的教學活動是學生學與教師教的統一，學生是學習的主體，教師是學習的組織者、引導者與合作者。”所以，真正有效、真正高效的數學課堂，是讓學生思維活動起來的課堂，是時間效率與學生思維效率高度和諧統一的課堂。而沒有學生思維真正參與的數學課堂，無論它呈現了多么豐富的內容，都不是高效的課堂。本課通過對教材的“微創”，加入局部的探究元素，既兼顧了時間效率，又提升了學生的思維效率，因而，課堂效率是很高的。《課標》（2011版）還指出，“義務教育階段的培養目標，要面向全體學生，適應學生個性發展的需要，使得：人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展”。對教材的“微創”，就是通過設計開放性的探究活動、探究問題，讓學生在探究中找到適合自己的方法，在活動中、在教師的引導下，按照自己已有的知識經驗主動建構出新的知識與方法，這樣獲得的知識才是有個性特征的知識，才真正達到了課程標準的上述要求，而能夠達到這種要求的數學課堂教學，才是真正有效的教學。

由于學生接受知識的學習過程是一個動態過程，因此“靜的教材”不可能與“動的學生”做到很好的吻合。教師在進行教學時，絕不能“照本宣科”，要學會客觀地看待教材，自主創新地選擇、組織和使用教材，認真做好教材的“二次開發”，最好是“微創”，從而在尊重教材的基礎上激發學生的學習興趣，把學生從“被動學習”的狀態轉化為“主動學習”的狀態，有效培養學生的自主創新精神。值得注意的是，“微創”教材時要做到兩點：“眼中有學生”、“胸中有教材”，要以教材為載體，視學生的實際情況和具體的教學內容而創造，絕不能“脫離教材”、“脫離學生”。

參考文獻

[1] 中華人民共和國教育部制定.義務教育數學課程標準解讀（2011年版）[M].北京：北京師范大學出版社，2011.

[2] 楊裕前，董林偉主編.數學.八年級（下冊）[M].南京：江蘇科學技術出版社，2013.

[3] 張林.例題選講忌隨意[J].中學數學教學參考（中旬），2012（12）.

【責任編輯 ?郭振玲】