鐵路集裝箱運輸時間可靠性分析
張 戎, 簡文良, 諸立超
(同濟大學 交通運輸工程學院 道路與交通工程教育部重點實驗室, 上海 201804)
可靠性指產品或系統在壽命周期內的特定時間段執行預期功能的能力。在交通領域,道路網絡的可靠性評價包括連通可靠性、行程時間可靠性、路網容量可靠性。近幾年,客運可靠性研究日漸升溫,并取得豐富成果,包括路徑選擇[1]、出行方式選擇[2]、道路收費[3]和運輸系統管理[4]等方面的應用。隨著產業結構調整,零庫存、JIT生產等先進理念應用于企業管理中,貨運可靠性也日益受到重視。目前,國外貨運可靠性研究主要集中在效用函數、庫存理論和成本函數3個方面。效用函數以隨機效用最大化理論模擬決策者選擇行為,可靠性作為重要的運輸屬性變量納入效用函數中分析其影響程度,這種方法多用于貨運需求分析[5]和政策評價[6];庫存理論[7]以經典庫存理論為基礎,分析運輸可靠性對訂貨提前期的影響,進而對企業安全庫存產生約束,用于分析可靠性與安全庫存成本之間的關系。然而,立足于庫存成本并未考慮可靠性帶來的其他成本影響,獲得的可靠性價值偏低;成本函數[8]不僅考慮可靠性對安全庫存的影響,同時分析可靠性對生產成本函數的影響。因此,更加全面地描述企業的運輸決策過程。國內研究中,張戎等[9]通過托運人定性打分的方式評價公路和鐵路運輸鏈的可靠性并分析其重要性;謝如鶴[10]指出貨物運輸可靠性是鐵路運輸的重要服務屬性,并建議改善運輸組織以保證貨物及時送達;李夏苗和胡思繼等[11]用β函數描述直達列車全程旅行時間的特征,并得到直達貨物運輸按時送達的可靠性水平。
可靠性價值是可靠性研究的重要組成部分。以往時間價值是基礎設施建設評估中重要的指標,現在可靠性價值在交通設施評價中逐漸受到關注。客運領域,時間價值和可靠性價值的研究成果豐富;貨運領域,Kurri等[12]通過對瑞典貨物運輸的研究,得到公路可靠性價值為47.47美元/(t·h),鐵路為0.5美元/(t·h);De Jong等[6]研究得到可靠性價值與時間價值的比值(RR,reliability ratio)為1.24。
本文選取蚌埠—上海集裝箱運輸鏈為研究對象,分析鐵路運輸鏈的可靠性及對鐵路運輸競爭力的影響,主要創新點體現在以下3方面:
(1) 根據貨運特征定義可靠性,建立不同的可靠性度量指標,定量描述鐵路運輸鏈的可靠性;
(2) 采用離散選擇模型研究可靠性對貨運方式選擇的影響程度,計算蚌埠—上海集裝箱運輸的時間價值和可靠性價值;
(3) 通過模型精度比較2種可靠性指標在貨運方式選擇中的優劣,并為鐵路運輸鏈的改善提出建議。
1 可靠性度量
1.1 預期運輸時間
貨運可靠性指貨物實際運輸時間與托運人預期運輸時間的差異,是描述多次貨物運輸時間波動的指標。其中對托運人預期運輸時間的假定是可靠性研究的重要內容。在既有研究中,De Palma和Picard[13]采用樣本均值作為出行者的預期時間;Brownstone和Small[3]以運輸時間分布的90%和50%分位數作為出行者可接受出行時間的上下限;Tilahun和Levinson[1]則提出樣本眾數(即抽樣樣本中出現次數最多的數值)可較好表征出行者預期運輸時間。
假設托運人對運輸時間的預期是基于以往的運輸經驗,那么預期運輸時間應該是托運人在托運過程中出現頻數最高的運輸時間。運輸時間的波動是隨機的,對隨機變量的預測應采用1個區間而非具體數值,所以托運人預期運輸時間采用某個時間段更加合理。綜上所述,本文選取運輸時間直方圖中頻數最高的時間段(見圖1)作為托運人預期運輸時間。
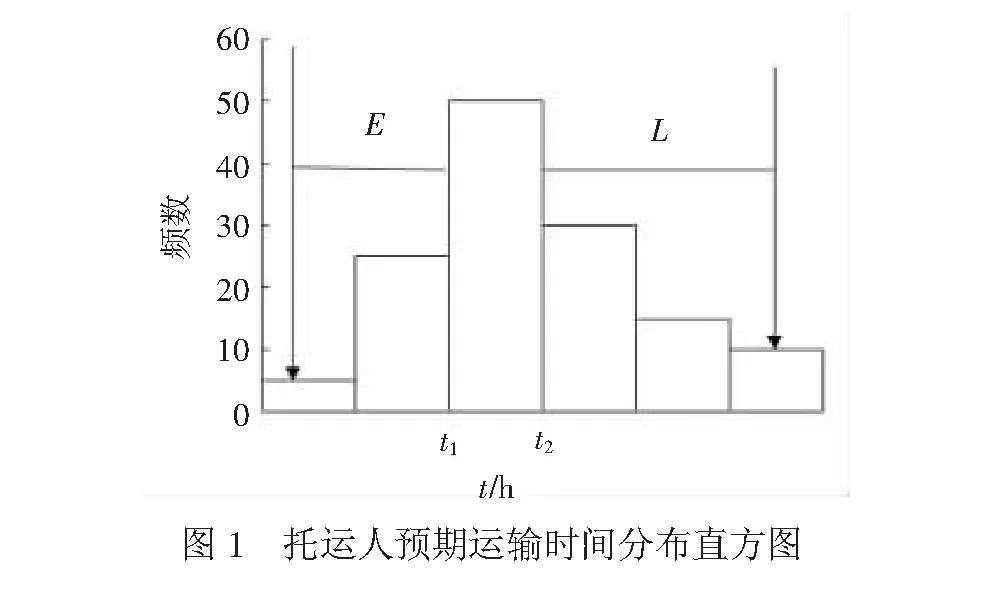
1.2 可靠性度量指標
確定可靠性度量指標是研究可靠性的另一個重要內容。De Jong等[6]采用樣本方差作為度量指標研究荷蘭國內貨運的可靠性價值;Noland和Small[14]定義平均提前到達時間和平均延誤時間2個量作為出行者度量行程時間可靠性的指標;Tilahun和Levinson[1]則以延誤概率為指標研究出行者路徑選擇問題。
以上3項可靠性指標是目前研究中最常見的度量指標。樣本方差作為可靠性度量指標不能區分提前到達和延誤到達的影響。貨物運輸中,提前到達使得庫存成本增加,而延誤到達則造成錯過船期等重大損失,因此對兩者分別考慮更加合理。將平均提前到達時間和平均延誤時間作為衡量指標的研究中,提前到達時間量對決策者的影響并不顯著,各度量指標的優劣尚未有統一定論,應根據具體案例建模后進行比較。
本文采用2種度量指標對鐵路集裝箱運輸可靠性進行研究。首先,定義平均提前到達時間和平均延誤時間作為第1種衡量指標,計算式為
( 1 )
( 2 )
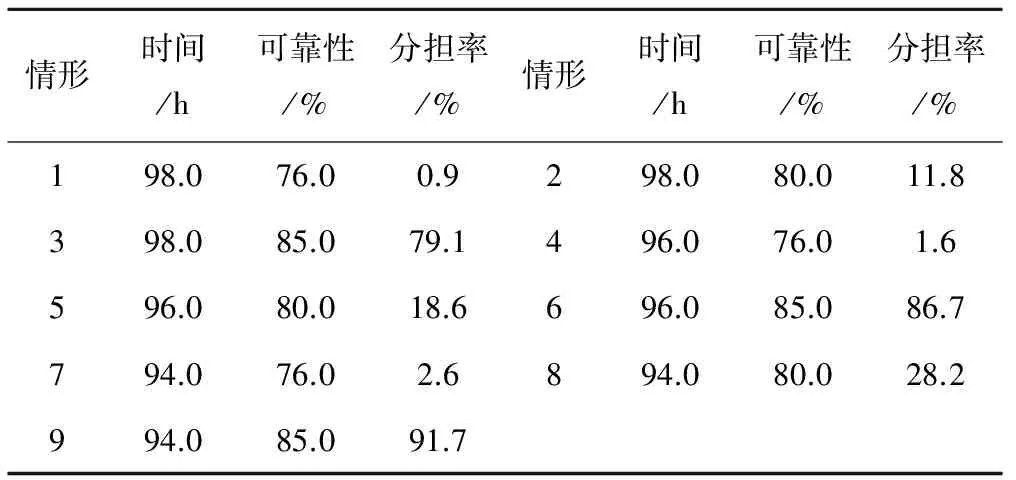
式中:E為平均提前到達時間;L為平均延誤時間;ti為實際運輸時間;T為預期運輸時間;pi為運輸時間ti的出現概率;δi為虛擬變量,t1、t2為運輸時間直方圖中頻數最高的時間段端點,t1 其次,采用及時送達概率作為第2種衡量指標,計算式為 ( 3 ) 式中:P為及時送達的概率。 根據實地調研,由于蚌埠市政府對海鐵聯運的集裝箱給予每TEU (twenty-feet equivalent unit,國際標準箱單位)870元補貼,使鐵路運輸競爭力大于公路,水路則以低廉的運費在集裝箱運輸市場占有很大份額。因此,蚌埠—上海的集裝箱運輸主要為鐵路和水路2種方式。在這2種運輸方式中,水路運輸鏈是通過公路短駁由蚌埠運至南京,再轉水運到達上海外高橋港區或者洋山港區;鐵路運輸鏈則先由公路短駁至鐵路蚌埠東站,然后經貨運班列運至上海南翔編組站,經解編后發送至蘆潮港或楊浦站,最后通過公路短駁運達港區。本文選取鐵路和水路運輸鏈作為貨運方式選擇模型的2個備選方案,為研究可靠性對貨運方式選擇的影響程度,選取運輸鏈費用、時間和可靠性作為貨運方式選擇的主要影響因素。 論文獲取的數據分為3類,第1類為蚌埠—上海的鐵路和水路集裝箱運輸鏈費用、時間及可靠性經驗值,來源于蚌埠鐵路貨運站工作人員以及當地貨代企業代表的訪談,作為SP(stated preference,意向調查)調查提供情景設置依據,保證SP問卷中運輸方式的屬性值更加貼近實際;第2類為蚌埠—上海鐵路集裝箱運輸鏈時間數據,來源于蚌埠鐵路貨運站數據庫,共收集2014-04-01~2014-04-30由蚌埠東站發送至上海楊浦站的運輸時間,共159條用于分析鐵路集裝箱運輸時間的可靠性;第3類為SP數據,SP調查中,每份問卷設置4個假設情景,每個情景包含水路和鐵路2種備選運輸方式,每種運輸方式包含時間、費用、可靠性3種運輸屬性。以第1類數據為基礎,分別對費用、時間設置3個變化水平,對可靠性設置3個變化水平,采用正交設計共生成16組方案。考慮到每位受訪者完成16組情景選擇任務量過大,因此每份問卷僅設置4組場景,每4份問卷構成1套完整方案。調查對象為蚌埠市16家貨主貨代企業代表,共獲取520條有效SP數據,用于模型參數估計。 根據采集的數據,鐵路運輸鏈費用包含鐵路運費、短駁運費、裝卸費用以及政策補貼,蚌埠—上海的鐵路集裝箱運輸鏈費用組成,見表1。其中,870元/TEU是蚌埠市政府對一次辦理達到200TUE的托運人進行補貼,以此提高鐵路集裝箱運輸量,中小企業為獲取補貼更愿意選擇通過貨代辦理鐵路運輸。經企業訪談,蚌埠—上海水路集裝箱運輸鏈費用低于鐵路,約為2 500元/TEU,水路運輸鏈時間則比鐵路運輸鏈時間長,為120 h。 表1 鐵路集裝箱運輸鏈費用 元·TEU-1 鐵路集裝箱運輸鏈時間包括首末端短駁運輸時間、鐵路運輸時間和鐵路堆存時間,本文主要對獲取的159條鐵路運輸時間進行分析,得到蚌埠—上海鐵路集裝箱運輸平均時間為98 h,運輸時間直方圖見圖2,進一步根據可靠性定義得出鐵路運輸可靠性,見表2。 表2 鐵路運輸時間的可靠性 衡量指標E/hL/hP/%可靠性值1.292.2676.00 根據隨機效用最大化理論,當且僅當式( 4 )成立時,決策者選擇第i個備選方案。 Uin>Ujni,j∈Cj≠i ( 4 ) 式中:i、j為備選方案;C為備選方案集合;Uin為決策者選擇第i個備選方案的效用;Ujn為決策者選擇第j個備選方案的效用。 備選方案效用是1個隨機變量,由確定性的效用項和隨機的效用誤差組成。固定項是屬性變量(通常包括備選方案屬性變量和決策者特征變量)的函數,效用誤差描述研究者無法觀察到的因素對方案效用的影響。 Uin=Vin+εin ( 5 ) 式中:Vin為決策者n選擇第i個備選方案的確定性效用項;εin為決策者n選擇第i個備選方案的隨機效用項。 考慮到結果分析和參數標定的方便性,通常采用線性函數描述固定項,即 ( 6 ) 式中:Xinl為決策者n選擇第i個備選方案中的第l個變量;L為第i個備選方案的變量個數;θl為第l個變量的待定系數。 假定每個備選方案的效用隨機誤差項均服從二重指數分布,根據備選方案的聯合累積分布函數可知各備選方案的選擇概率為 ( 7 ) 式中:Pin為決策者n選擇備選方案i的概率;jn為備選方案集合。 根據前面確定的選擇枝和影響因素,建立鐵路和水路運輸鏈效用函數。 選取平均提前到達時間和平均延誤時間作為可靠性衡量指標的效用函數為 Urail=Vrail+εrail= ASC+θ1Crail+θ2Trail+θ3Erail+θ4Lrail+εrail Uwater=Vwater+εwater= θ1Cwater+θ2Twater+θ3Ewater+θ4Lwater+εwater 式中:Urail、Uwater分別為選擇鐵路和水路運輸的效用;Vrail、Vwater分別為選擇鐵路和水路運輸的效用固定項;εrail、εwater分別為選擇鐵路和水路運輸的效用隨機項,均服從參數為(0,1)的二重指數分布;Crail、Trail、Erail、Lrail分別為鐵路運輸的費用、時間、平均提前到達時間、平均延誤時間;Cwater、Twater、Ewater、Lwater分別為水路運輸的費用、時間、平均提前到達時間、平均延誤時間;θ1、θ2、θ3、θ4均為待定參數;ASC為常數項。 選取及時送達概率作為可靠性衡量指標的效用函數為 Urail=Vrail+εrail= ASC1+θ1Crail+θ2Trail+θ5Prail+εrail Uwater=Vwater+εwater= θ1Cwater+θ2Twater+θ5Pwater+εwater 式中:Prail、Pwater分別為鐵路和水路運輸的及時送達概率;θ5為待定參數;ASC1為常數項。 根據獲取的SP數據,通過NLOGIT軟件,對MNL模型進行參數估計和檢驗,結果見表3。 表3 模型參數估計結果 注:*** 為顯著水平在99%以上;** 為顯著水平在95%~99%之間;* 為顯著水平在90%~95%之間。 從表3可看出運輸鏈費用和時間的參數估計值顯著性高,并且在不同可靠性指標的模型中,參數估計值相差不多,符合預期結果。2種可靠性指標的參數估計值顯著性較高,其中E指標的參數值顯著性與其他變量相比較低,說明提早到達對托運人的方式選擇影響較小,與文獻[15]的研究結論一致。 從表3的對比可看出P模型在優度比上優于另一模型,即該模型更好地擬合托運人的選擇結果。因此在對分擔率的預測中選取擬合精度更高的及時送達概率為可靠性指標。利用模型參數估計結果,分別以θ2、θ3、θ4、θ5和θ1之比得到蚌埠—上海集裝箱運輸的時間價值和可靠性價值,結果見表4。 表4 貨運時間價值與可靠性價值 根據表4測算結果可知兩類模型的貨運時間價值相差無幾,約為40元/h,而貨運可靠性價值明顯高于時間價值。由E&L模型得到的提前到達可靠性價值比時間價值高24%,而延誤到達可靠性價值比時間價值高136%,說明與提前到達相比,托運人更在意是否造成延誤,提前到達雖然增加部分庫存成本,但延誤到達造成的損失更大。而P模型得到的貨運可靠性價值更高,但由于單位不同不能直接進行比較。如果利用鐵路運輸鏈平均時間98 h和平均可靠性76%做換算,得到貨運可靠性價值為79.82元/h,介于E&L模型得到的提早到達和延誤到達的可靠性價值之間。總之,使用E&L模型測算可靠性價值更加合理,但就模型精度而言,P模型更優。 彈性是衡量選擇概率對某影響因素變動的反應程度,計算如下 ( 8 ) 式中:Pi為選擇概率;xj為影響因素;?pi為pi的變化值;?xj為影響因素xj的變化值。 根據參數估計結果計算運輸鏈選擇概率的影響因素彈性,見表5。 表5 影響因素彈性 由表5可知,選擇概率的可靠性彈性高于時間和費用彈性,說明可靠性對貨運方式選擇的重要影響;水路運輸鏈的影響因素彈性高于鐵路,說明水路運輸對這些影響因素的變化更為敏感。 蚌埠—上海集裝箱鐵路和水路運輸鏈屬性值見表6。當地政府對鐵路集裝箱運輸的補貼高達870元/TEU,增強鐵路集裝箱運輸的競爭力,是蚌埠鐵路無水港投入使用初期為增加鐵路集裝箱運量采取的鼓勵措施,但政策性補貼不是長久之計,未來勢必減少甚至取消,有必要對減少補貼下的鐵路運輸鏈競爭力進行評估。根據表3中P模型的參數估計值和表6中鐵路與水路運輸鏈的屬性值,計算得到政策補貼減少為600元/TEU、400元/TEU、200元/TEU以及取消后鐵路分擔率的變化,見表7。 表6 鐵路與水路運輸屬性值對比 表7 不同政策補貼下鐵路分擔率預測 根據表7預測結果可知蚌埠市政府減少補貼費用后,鐵路運輸分擔率將迅速下降。此時,鐵路部門如何優化運輸費用、時間、可靠性等運輸鏈屬性值是增強鐵路競爭力的關鍵問題。目前,鐵路集裝箱運輸業務辦理流程復雜,作業效率較低,集裝箱運量季節性波動大、兩端短駁銜接不暢等是影響鐵路集裝箱運輸時間及可靠性的主要因素。通過優化集裝箱業務辦理流程、推廣“接取送達”服務以及依據集裝箱需求及時增開集裝箱班列等措施能夠有效降低鐵路運輸時間和提高可靠性。據調研,如采取以上措施,預計鐵路運輸鏈時間可縮短2 h~4 h,可靠性可增加至85%左右。 表8給出補貼費用取消后,鐵路運輸鏈時間分別為98 h、96 h、94 h和可靠性分別為76%、80%、85%時的鐵路運輸鏈分擔率。可以看出:當可靠性不變時,運輸時間的減少對鐵路分擔率影響較小;而運輸時間不變時,可靠性的提高使得鐵路分擔率急劇增長,即鐵路分擔率對可靠性變化的靈敏度高于運輸時間的變化。水路運輸相比于鐵路運輸,在運輸費用上具有比較明顯的優勢,而鐵路運輸在運輸時間及其可靠性等屬性上優于水路運輸。從表7預測結果說明,補貼政策對鐵路運輸的競爭力影響大;從表8預測結果說明,鐵路分擔率對于可靠性變化的敏感度要高于運輸時間變化。因此,提高運輸時間可靠性是增強鐵路集裝箱運輸競爭力的重要途徑。 表8 不同時間及可靠性的鐵路分擔率 本文針對鐵路集裝箱運輸可靠性進行定量研究,以蚌埠—上海集裝箱運輸鏈為研究對象,選取運輸鏈費用、時間及可靠性為貨運方式選擇影響因素,采用E&L和P為可靠性指標,建立2類不同的MNL模型,通過模型參數標定和彈性分析揭示可靠性比時間和費用更為敏感,并根據實地調查確定改善可靠性對提高鐵路競爭力的影響。但文中僅給出鐵路運輸鏈可靠性、時間和費用的改善空間,如何改進可靠性、時間和費用等服務屬性有待進一步研究;今后可以逐步將貨物批量、貨物價值等因素納入影響運輸方式選擇的模型中。 參考文獻: [1] TILAHUM Y, LEVINSON D M. A Moment of Time: Reliability in Route Choice Using Stated Preference[J]. Intelligent Transport S, 2010, 14(3): 179-187. [2] BHAT C, SARDESAI R. The Impact of Stop-making and Travel Time Reliability on Commute Mode Choice[J].Transportation Research Part B, 2006, 40(9): 709-730. [3] BROWNSTONE D, SMALL K. Valuing Time and Reliability: Assessing the Evidence from Road Pricing Demonstrations[J]. Transportation Research Part A, 2004, 39(4): 279-293. [4] OH J, CHUNG Y. Calculation of Travel Time Variability from Loop Detector Data[J]. Transportation Research Record, 2006, 1945:12-23. [5] WINSTON C. A Disaggregate Model of the Demand for Intercity Freight Transportation[J]. Econometric Journal of the Econometric Society, 1981,49(4):981-1006. [6] DE JONG G, KOUWENHOVEN M, KROES E, et al. Preliminary Monetary Values for the Reliability of Travel Times in Freight Transport[J]. EJTIR, 2009,2(9):83-99. [7] DULLAET W, ZAMPARINI L. The Impact of Lead Time Reliability in Freight Transport: A Logistics Assessment of Transport Economics Findings[J]. Transportation Research Part E,2013,49(1):190-200. [8] BOLIS S, MAGGI R. Logistics Strategy and Transport Service Choices: An Adaptive Stated Preference Experiment[J].Growth and Change, 2002, 34(4): 490-504. [9] 張戎,郭玉靜,閆哲彬,等.基于 Nested-Logit 模型的托運人運輸鏈選擇行為研究[J]. 鐵道學報, 2011, 33(7): 8-13. ZHANG Rong, GUO Yu-jing, YAN Zhe-bin, et al. Study on International Container Transportation Chain Choice Behavior Based on Nested-Logit Model[J]. Journal of the China Railway Society, 2011, 33(7):8-13. [10] 謝如鶴, 秦四平. 保證貨物及時送達的運輸組織技術研究[J] 中國鐵道科學, 2001,22(1):90-93. XIE Ru-he, QIN Si-ping Ensure Timely Delivery of Goods Transport Organization Technology Research[J].China Railway,2001,22(1):90-93. [11] 李夏苗, 胡思繼, 朱曉立. 直達貨物運輸按時送達可靠性的評估方法[J].中國鐵道科學, 2003, 24(1): 121-124. LI Xia-miao, HU Si-ji, ZHU Xiao-li. A Method for Evaluating Reliability of Through Transport of Freight on Schedule[J].China Railway Science, 2003,24(1): 121-124. [12] KURRI J, SIRKIA A, MIKOLA J.Value of Time in Freight Transport in Finland[J]. Transportation Research Record, 2000, 1725: 26-30. [13] DE PALMA A, PICARD N. Equilibria and Information Provision in Risky Networks with Risk-averse Drivers[J]. Transportation Science, 2006, 40(4): 393-408. [14] NOLAND R B, SMALL K. Simulating Travel Reliability[J]. Regional Science &Urban Economics, 1998, 28(5): 535-539. [15] SMALL K. The Scheduling of Consumer Activities: Work trips[J]. The American Economic Review, 1982, 72 (3): 467-479. [16] 關宏志. 非集計模型[M] .北京:人民交通出版社, 2004:50-70.2 構建模型
2.1 蚌埠—上海集裝箱運輸鏈
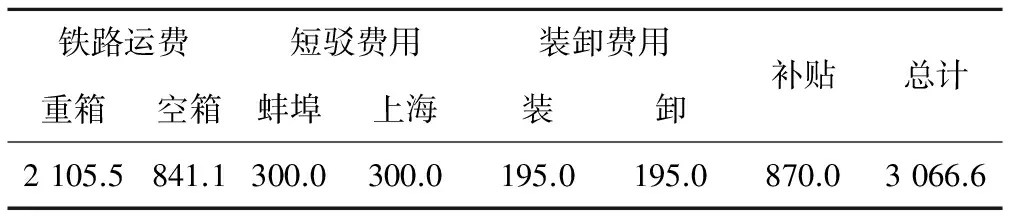
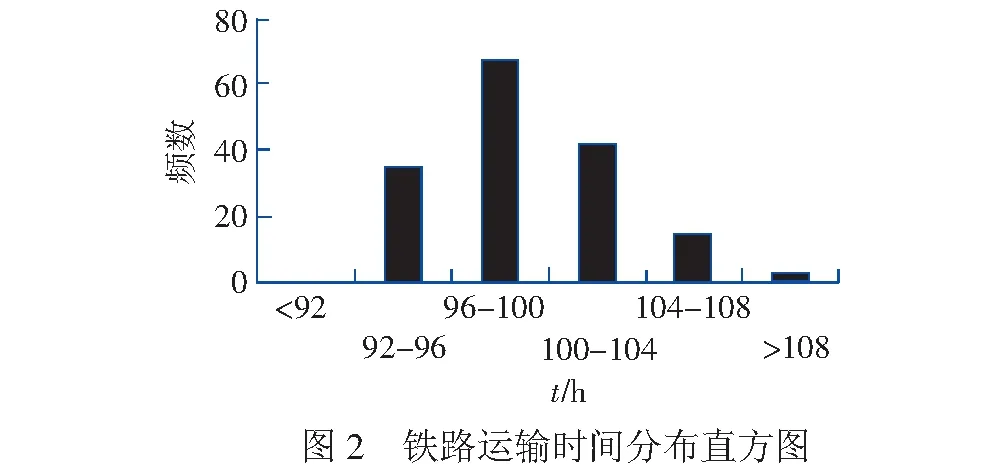

2.2 MNL (Multinomial Logit) 模型
3 參數估計與分析
3.1 參數標定


3.2 彈性分析

3.3 敏感性分析

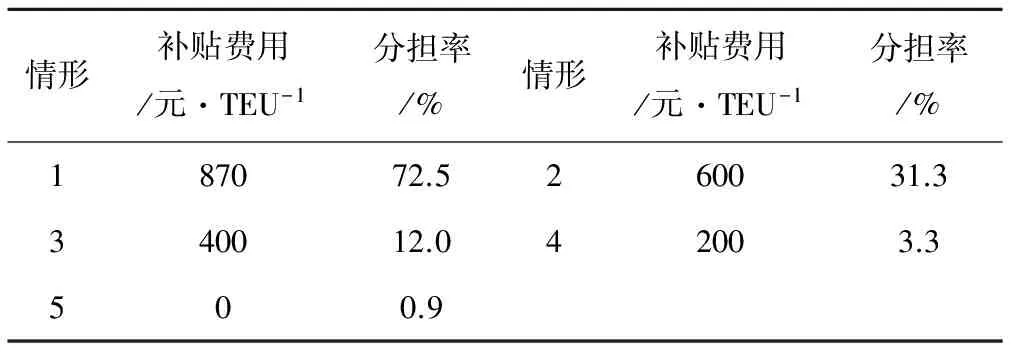
4 結語

