基于健康指數的軌道電路設備壽命預測方法的研究

張鳳霞，米根鎖

蘭州交通大學 自動化與電氣工程學院，甘肅 蘭州 730070)

軌道電路作為鐵路信號系統中重要的基礎設備之一，其能否安全、可靠地運行直接影響到運輸效率和行車安全。目前，鐵路部門對信號設備的更新決策往往以在役時間長短作為設備更換的依據，ZPW-2000A軌道電路作為信號系統中最典型的設備之一，對其設備進行剩余壽命預測，具有一定的現實意義。

近年來，對于軌道電路設備維修和故障診斷方法等方面的研究頗多。文獻[1]運用可靠性分析方法中的故障模式及影響分析方法對軌道電路設備的維修進行了研究。文獻[2]在故障模式及影響分析的基礎上對設備故障影響進行分類，依據邏輯決策圖進行維修方式決策。文獻[3]根據軌道電路的工作原理和故障特點建立了模糊神經網絡的故障診斷模型。文獻[4]基于傳輸線理論提出機車信號感應電壓幅值包絡仿真模型，運用遺傳算法對軌道電路的故障進行了綜合評判。不難看出，對軌道電路維修的研究還局限于故障診斷和可靠性等方面，而隨著鐵路信息化的發展及大量新技術的使用，需要對軌道電路設備的實際性能進行分析和預測。在航空、電力等領域，在設備狀態評估和壽命預測方面已展開了大量的研究[5-7]。而在鐵路領域，文獻[8]對發送器和接收器的壽命進行了分析，做出了相應的壽命分布，但其只收集了原始數據，并沒有對設備的狀態做出判斷，缺乏對設備實際性能的準確分析。目前，對設備健康分析和壽命預測的研究還處于起步階段。

本文建立了完整的ZPW-2000A軌道電路設備壽命預測模型，包括設備的健康狀態評價模型和壽命預測模型，通過對設備壽命的預測，不僅可以得到設備當前的剩余壽命，還可以反映健康指數與運行時間的變化規律，實現對軌道電路設備實際性能的實時分析。

1 ZPW-2000A軌道電路設備健康指數模型

影響ZPW-2000A軌道電路健康狀態的因素眾多，這些因素之間的關系錯綜復雜，且對結果的影響具有模糊性，因此采用基于模糊綜合評判法的軌道電路設備健康指數評價模型，將ZPW-2000A軌道電路設備健康狀態量化，量化的結果定義為軌道電路設備的健康指數HI(Health Index)。HI是反映軌道電路健康程度的指標。規定HI的取值范圍為0～100。HI越接近100表明軌道電路的健康程度越高，HI越接近0表明軌道電路的健康程度越低，定義HI=60為臨界值，即軌道電路設備應大修或更換，已到達使用年限。當HI>60時系統運行正常，當HI<60時系統故障[9]。軌道電路健康指數定量指標與健康狀態定性評價等級之間的映射關系見表1。

表1 ZPW-2000A軌道電路健康狀態等級

建立ZPW-2000A軌道電路健康指數模型的步驟如下。

(1)確定指標體系U

綜合考慮設備的歷史與現狀、電氣與非電氣因素以及運行狀況等，選取運行數據、設備基本情況和運行工況3個方面對ZPW-2000A軌道電路設備的健康狀態進行分析。其中軌道電路的運行數據是指從設備投入運行開始，隨著時間所積累下來的關于設備狀況的信息，包括運行前的基礎數據、檢修記錄、運行時間等。設備基本情況是設備自身特征的體現，如技術參數、家族質量史、性能效果等，從靜態的角度反映設備安全運行相關的能力。ZPW-2000A軌道電路設備的運行工況是由所評估設備的實時運行狀態和運行環境反映出來的，是從現實的、動態的角度構成設備運行的安全狀態。因此建立ZPW-2000A軌道電路設備健康狀態評價體系如圖1所示。根據圖1建立ZPW-2000A軌道電路健康狀態評估因素集U={u1,u2,…,u6}，其中ui代表評估對象的6種影響因素。

圖1 軌道電路系統的健康狀態評價體系

(2)建立評語集V

vi代表每個影響因素的n種評判結果。由于軌道電路的健康是一個模糊的概念，因此根據軌道電路運行特點將軌道電路健康程度劃分為健康、亞健康、異常、故障4個等級。V={v1,v2,v3,v4}，其中vj(j=1,2,3,4)表示第j個評價等級，根據表1，即V={100,85,70,60}。

(3)建立權重集A

建立指標體系后，需對各指標賦予相應的權重，本文采用層次分析法確定各指標權重。

(4)確定單因素評判矩陣R

設評估對象按因素集中的第i個因素進行評估，評判集中第j個元素的隸屬度為rij，則評估結果用模糊集合Ri={ri1,ri2,ri3,ri4}表示。因此需確定評估對象對評判集的隸屬度。對于定量指標，引入相對劣化的概念，利用半梯形和三角形組合的分布函數，建立各指標不同狀態等級的隸屬函數，而對于定性指標則采用模糊統計法，應用專家打分法來確定各指標的隸屬度。

(5)確定模糊綜合評判模型

單因素模糊評判，僅反映了單個因素對評估對象的影響，而對于多因素影響評估對象的問題，需綜合單因素評估的結果。因此，軌道電路健康狀態的模糊綜合評判矩陣為

=b1b2b3b4

( 1 )

(6)綜合評價結果HI

( 2 )

式中：vj為評語集V中的元素。

( 3 )

式中：bj為式( 1 )中矩陣B的元素。

2 ZPW-2000A軌道電路設備剩余壽命預測模型

隨機模糊理論是一門研究隨機模糊雙重不確定現象的數學分支，文獻[10]于2002 年在概率論與可信性理論的基礎上，提出期望值算子、關鍵值及機會分布等概念和隨機模糊變量的定義，建立起完整的隨機模糊理論，為處理隨機模糊變量提供了理論依據。隨機模糊變量是從可信性空間到隨機變量構成的集合的函數，描述隨機模糊事件。

ZPW-2000A軌道電路設備主要由室內和室外兩部分構成，大多屬于電子設備，在運行過程中隨著時間的增加，同時受到各種不確定因素的影響，如運行環境、設備自身的質量、維護檢修狀況等，而這些影響因素既具有隨機性又具有模糊性，因此本文選取隨機模糊理論對設備的壽命進行預測。

2.1 ZPW-2000A設備的壽命特征曲線

ZPW-2000A軌道電路設備隨著運行時間的增加，老化程度增加，導致系統的整體性能不斷退化，直至失效。圖2的P-F曲線[11]描繪了設備狀態劣化的過程，在t1時刻設備出現運行缺陷，這種潛在缺陷會隨著設備的繼續使用而進一步加劇，使得其整體性能不斷下降，在到達某一時刻t2時，其整體性能下降到所允許的極限值，就會出現故障。

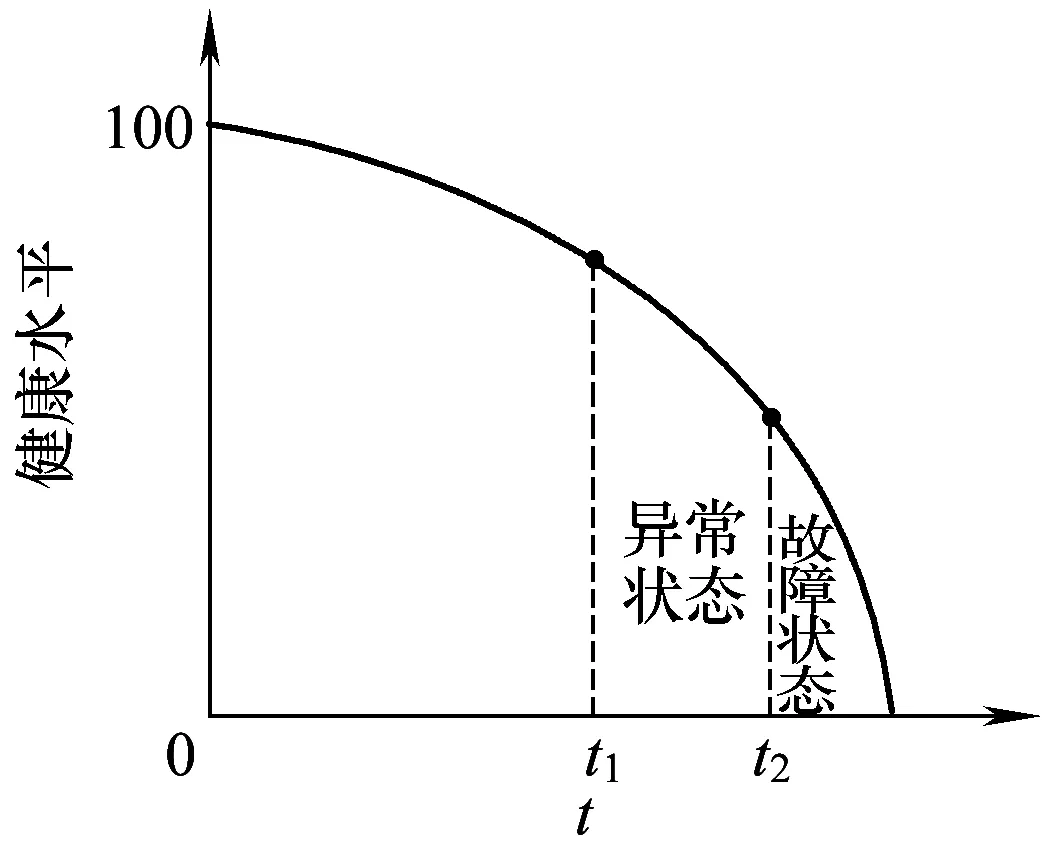
圖2 P-F曲線

P-F曲線反映了設備狀態隨時間的變化規律，由圖2可以看出，其狀態呈指數規律下降。

2.2 確定健康指數的隨機模糊分布函數

根據鐵路信號微機監測系統的記錄數據和ZPW-2000A軌道電路設備生產與現場返修數據，應用基于模糊綜合評判的軌道電路設備健康狀態評估模型計算得到軌道電路設備的歷年健康指數。本文以ZPW-2000A軌道電路發送器為例，通過對發送器歷年健康指數數據分析可知，發送器的健康狀態呈指數規律下降。為了準確描述ZPW-2000A軌道電路發送器健康指數的分布，本文在隨機模糊理論的基礎上，采用隨機模糊分布來表示發送器的健康指數分布規律。

根據計算的發送器健康指數，應用Matlab最小二乘曲線擬合法得到發送器健康指數的指數分布如圖3中實線所示。由圖3可以看出，根據健康指數的ZPW-2000A軌道電路設備壽命規律與圖2基本吻合。

圖3 設備健康指數隨運行時間的變化曲線

健康指數分布函數為

HI(t)=a0+bect

( 4 )

式中：a0、b、c為常數。

根據曲線HI(t)=a0+bect，平移得到HI(t)=a1+bect和HI(t)=a2+bect，如圖3所示。進而將健康指數的指數分布函數中的參數a0用三角形模糊變量a=(a1,a0,a2)表示。

因此，ZPW-2000A軌道電路發送器的健康指數與運行時間可表示為隨機模糊分布函數，如式( 5 )所示。

HI(t)=a+becta=(a1,a0,a2)

( 5 )

2.3 建立隨機模糊理論壽命預測模型

根據所得到的ZPW-2000A軌道電路發送器健康指數對發送器的剩余壽命進行預測。發送器的剩余壽命是指在運行期間，其整體健康指數下降到允許的最低值之前能保持設備正常工作的最大時間，如式( 6 )所示。

T=max{t|HI(t)≥HIL}

( 6 )

式中：HIL為發送器所允許的最低健康指數。

結合式( 5 )和式( 6 )可得

a+bect≥HIL

( 7 )

變化曲線呈指數下降，因此有b<0，c>0，則式( 7 )經變換得到

( 8 )

對式( 8 )兩邊取對數得到

( 9 )

(10)

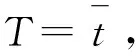
Tt=T-t

(11)

2.4 壽命預測模型的求解

一般的解析算法對隨機模糊問題進行求解通常是不現實的，文獻[12]提出了隨機模糊模擬技術，通過該技術對隨機模糊變量進行求解。

對于ZPW-2000A軌道電路設備隨機模糊變量壽命T，在給定的置信水平α、β下，根據2.3節的定義，通過隨機模擬計算滿足Pr{f(ξ(θk) )≥f(θk)}≥β的最大值f(θk)。首先從可信性空間Θ中均勻抽取樣本θk, 使其滿足Cr{θk}≥ε/2(k=1,2,…,N), 其中ε是一個充分小的正數，并令Vk=(2Cr{θk})∩1。對于每個θk，通過隨機模擬計算f(θk)=Pr{f(ξ(θk))≤0}，求解滿足L(r)≥α的最大值r，則最大值r即為要求解的軌道電路設備壽命T。其中

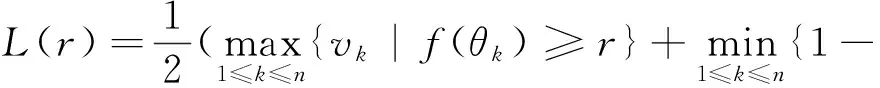
因此，對設備壽命預測模型的求解流程如圖4所示。

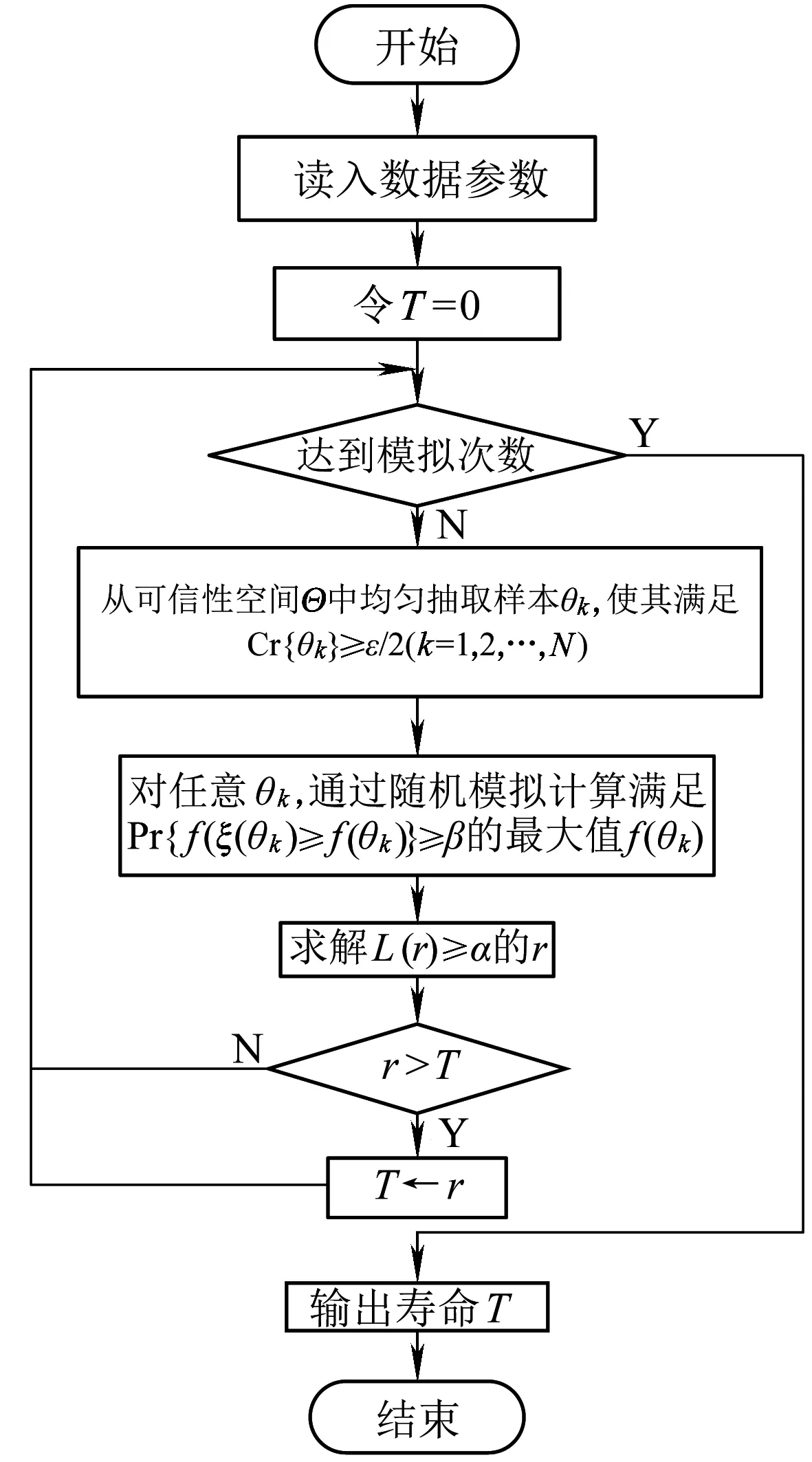
圖4 設備壽命預測模型求解算法流程圖

3 實例驗證及分析

現以某鐵路局一臺已運行12年的發送器為例，應用前述方法對其進行健康狀態評估和壽命預測，驗證本文提出的壽命模型的有效性和合理性。

根據現場數據和發送器技術條件，采用第 1 節論述的基于模糊綜合評判的健康狀態評估模型求此發送器的健康指數。

(1)指標權重的確定。采用層次分析法計算得到各指標權重見表2。

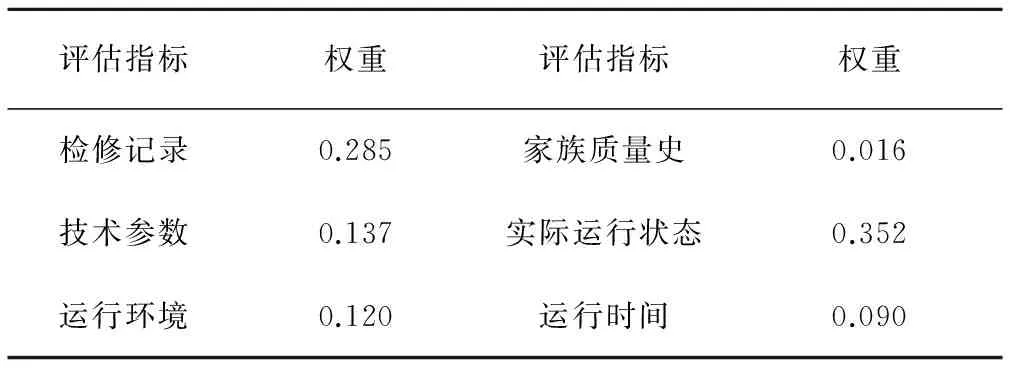
表2 指標權重

(2)指標分數的確定。根據設備的健康指數模糊綜合評判模型，針對不同的定量和定性指標，對定性指標的評分標準見表3,對定量指標運行時間采用降半梯形函數，如式(12)所示。

降半梯形函數

(12)

式中：a1，a2分別表示指標的注意值和最優值。對于運行時間，最優值為設備投入運行前的時間，即運行時間為0年；注意值為設備出廠規定的運行年限，該發送器的運行年限規定為30年，代入公式(12)得到X=0.6。指標分數采用百分制，60分為最低值，因此運行時間的指標分數轉化為

x=60+60×40%=84

定性指標綜合多位專家的評分，去掉一個最高分和一個最低分，求平均分即得指標分數。綜合相對劣化度和專家打分法，計算得到各指標的評分見表4。

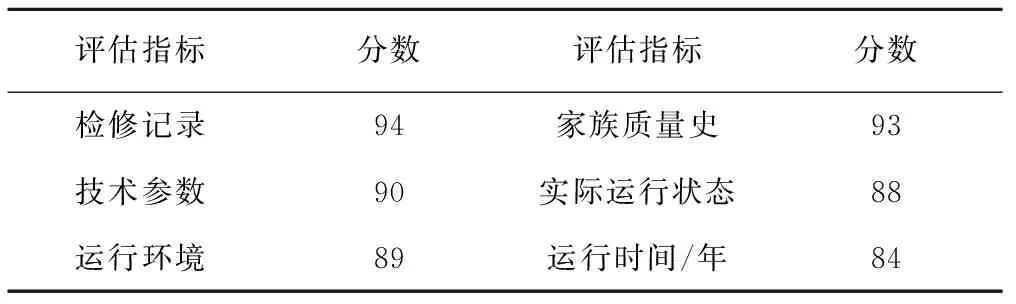
表4 指標評分

(3)發送器健康指數的計算。根據表2和表4所得的指標權重和指標所對應的分數，結合式( 2 )，計算發送器健康指數為

HI=0.285×94+0.137×90+0.120×89+

0.016×93+0.352×88+0.090×84=89.824

即發送器的健康指數HI為90，同樣的方法，計算發送器歷年的健康指數見表5。

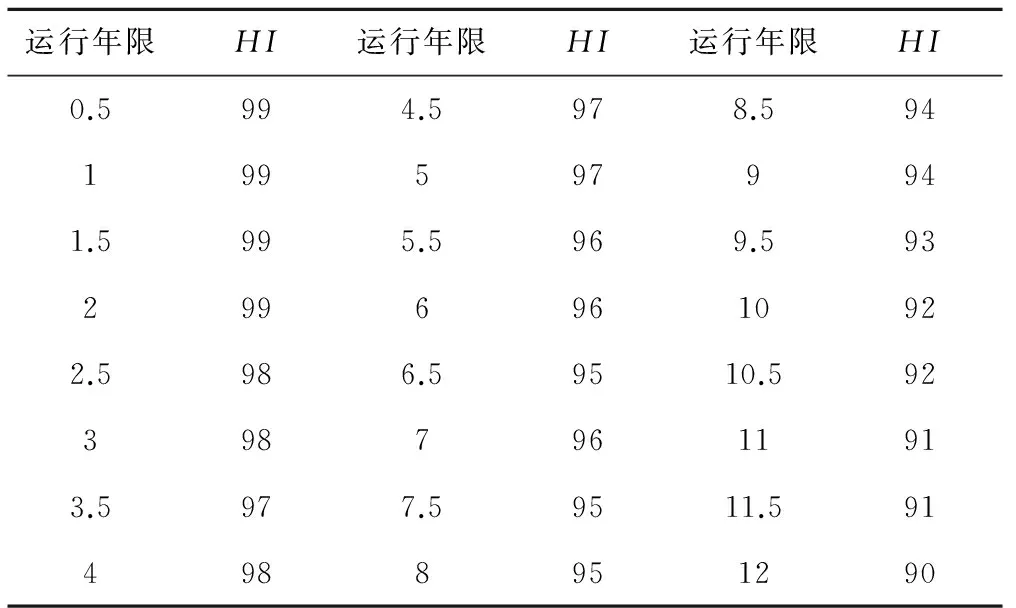
表5 發送器歷年的健康指數

由圖3中健康指數HI隨運行時間T的分布函數可以看出，發送器的健康指數隨運行時間呈指數規律下降。采用Matlab最小二乘曲線擬合法將表5中的設備歷年健康指數擬合，得到發送器健康指數分布如圖5所示。

圖5 發送器健康指數隨運行時間的變化曲線

根據圖5得到發送器的健康指數分布函數表達式為：f(x)=104.1-4.549×e0.093 57x，即圖5實線所示。經過平移，得到健康指數分布的兩條邊界線分別為：f(x)=100.6-4.549×e0.093 57x和f(x)=107.6-4.549×e0.093 57x。由此可以得到發送器的隨機模糊分布函數為

f(x)=a-4.549×e0.093 57x

(13)

將所得到的健康指數隨機模糊分布函數代入式(10)可得

(14)

4 結論

本文將模糊綜合評判法應用于ZPW-2000A軌道電路設備健康評估中，建立了適合ZPW-2000A軌道電路設備的健康指數模糊綜合評判模型。同時以健康指數為基礎，建立了基于隨機模糊理論的設備壽命預測模型，該預測模型能夠準確地反映出設備的健康指數隨著運行時間變化的規律。以一臺已運行12年的發送器為例，結合現場數據計算得到其歷年健康指數，再根據模糊隨機理論的壽命預測模型預測其壽命，預測結果給出了在一定的置信水平α=0.92,β=60下設備的壽命和剩余壽命，驗證了該方法的可行性。根據設備剩余壽命有效地掌握其實際性能，可以指導設備維修決策，為有關維修部門開展相應設備的狀態修提供科學依據，同時也為實現鐵路信號設備的壽命管理提供理論支撐。

參考文獻：

[1]單娜.基于FMEA和RCM的客專ZPW2000A軌道電路設備維修研究[D].成都：西南交通大學，2010：54-60.

[2]鄒瑤.以可靠性為中心的ZPW-2000A/K軌道電路設備的維修方法研究[D].成都：西南交通大學，2011：29-30.

[3]黃贊武，魏學業，劉澤.基于模糊神經網絡的軌道電路故障診斷方法研究[J].鐵道學報，2012，34(11)：54-59.

HUANG Zan-wu, WEI Xue-ye，LIU Ze. Fault Diagnosis of Railway Track Circuits Using Fuzzy Neural Network [J].Journal of the China Railway Society, 2012, 34(11): 54-59.

[4]趙林海，冉義奎，穆建成.基于遺傳算法的無絕緣軌道電路故障綜合診斷方法[J].中國鐵道科學，2010，31(3)：107-113.

ZHAO Lin-hai，RAN Yi-kui，MU Jian-cheng.The Method of Diagnosis of Fauliures with Jointless Track Circuits Based on Genetic Algorithm[J]. Journal of the China Railway Science, 2010, 31(3): 107-113.

[5]王吉星.基于人工神經網絡和遺傳算法的民航發動機狀態評估與故障診斷方法[D].天津：中國民用航空學院，2004：11-13.

[6]張翠玲，王大志，王安娜. 基于模糊AHP變壓器運行狀態判斷矩陣建立方法[J].東北大學學報：自然科學版，2013，34(3)：317-321.

ZHANG Cui-ling，WANG Da-zhi，WANG An-na. Establishment of Judgment Matrices for the Condition Assessment of the Power Transformer Based on Fussy AHP[J].Journal of Northeastern University:Natural Science, 2013, 34(3): 317-321.

[7]李東妍，榮命哲，王婷,等. 超高壓GIS剩余壽命評估方法綜述[J].高壓電器，2011，47(10)：87-92.

LI Dong-yan，RONG Ming-zhe，WANG Ting, et al. Review of Residual Sevice Life Estimation Method on Extra-high Voltage GIS[J]. High Voltage Apparatus, 2011, 47(10): 87-92.

[8]左飛. ZPW-2000A發送器與接收器壽命數據分析研究[D].成都：西南交通大學，2011：23-48.

[9]栗然，劉會蘭，盧云，等. 基于交叉熵理論的配電變壓器壽命組合預測方法[J].電力系統保護與控制，2014，42(2)：97-103.

LI Ran, LIU Hui-lan，LU Yun, et al. A Combination Method for Distribution Transformer Life Prediction Based on Cross Entropy Theory [J]. Power System Protection and Control, 2014, 42(2): 97-103.

[10]PENG J, LIU B. Uncertain Programming：Current Status and Future Prospects[J].Operations Research and Management Science, 2002, 11(2): 1-10.

[11]孟曉紅，周永濤，王煒.一種基于指數分布的裝備剩余壽命預測模型研究[J]. 中國修船，2012，25(5)：42-44.

MENG Xiao-hong, ZHOU Yong-tao, WANG Wei. A Kind of Equipment Residual Life Prediction Model Based on Exponential Distribution [J]. China Shiprepair, 2012, 25(5): 42-44.

[12] LI X, LIU B D. Chance Measure for Hybrid Event with Fuzziness and Randomness [J].Soft Computing, 2009, 13(2): 105-115.