參數(shù)約束系統(tǒng)的度量次正則性
張彬彬,王傳堅(jiān),靳巧花
(1.昆明理工大學(xué)理學(xué)院,云南 昆明 650500;2.云南大學(xué)旅游文化學(xué)院信息科學(xué)與技術(shù)系,云南 麗江 674100.)
參數(shù)約束系統(tǒng)的度量次正則性
張彬彬1,王傳堅(jiān)1,靳巧花2
(1.昆明理工大學(xué)理學(xué)院,云南 昆明 650500;2.云南大學(xué)旅游文化學(xué)院信息科學(xué)與技術(shù)系,云南 麗江 674100.)
運(yùn)用變分法和Clarke法錐,得到非凸參數(shù)約束系統(tǒng)具有度量次正則性的一個充分條件,并給出其在非線性參數(shù)約束系統(tǒng)中的一個應(yīng)用.
嚴(yán)格可微;Clarke 法錐;度量次正則性;參數(shù)約束系統(tǒng)
在數(shù)學(xué)規(guī)劃和向量優(yōu)化問題的誤差分析中,許多問題可歸結(jié)為形如F(x)∶={y∈Y|ɡ(x,y)∈Θ},x∈X的集值映射的度量正則性或次正則性,其中ɡ:X×Y→Z是單值映射,Θ?Z為閉子集.我們稱此集值映射為參數(shù)約束系統(tǒng)[1-4].集值映射的度量次正則性在數(shù)學(xué)規(guī)劃、誤差界的分析、弱極化最優(yōu)解等問題中起著非常重要的作用,近年來受到許多學(xué)者的廣泛關(guān)注.[5-9]目前得到的許多結(jié)論是在閉凸多值映射的假設(shè)下完成的,但事實(shí)上,諸多應(yīng)用問題和理論問題需要我們考慮非凸多值映射,最近許多學(xué)者在這方面也做了深入的研究.[3-4,8,10]
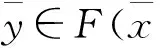
1 預(yù)備知識
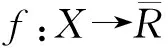
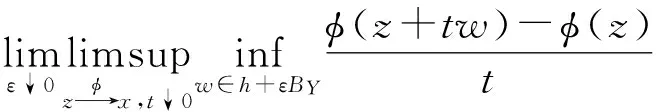
?cφ(x)∶={x*∈X*|〈x*,h〉≤φ↑(x,h),?h∈X}.
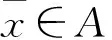

2 主要結(jié)論及證明
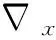
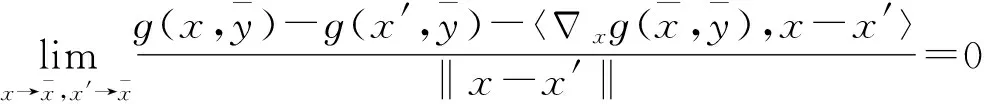
F(x)∶={y∈Y|ɡ(x,y)∈Θ},?x∈X.
(1)
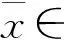
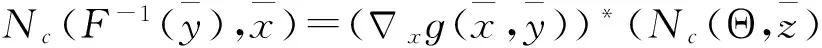
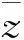
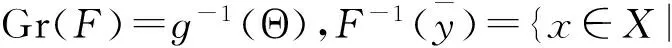
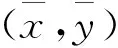
‖ɡ(x,y)-ɡ(u,v)‖≤M(‖x-u‖+‖y-v‖),
(2)
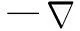
(3)
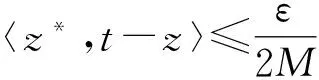
(4)
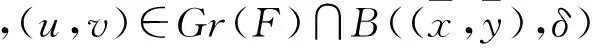
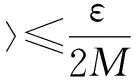
(5)
根據(jù)(3)及(5)式



(ε/2)(‖x-u‖+‖y-v‖)+(ε/2)(‖x-u‖+‖y-v‖)=ε(‖x-u‖+‖y-v‖).
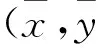

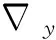
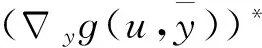
任取(u′,v′)∈X×Y,可得
〈(x*,y*),(u′,v′)〉=〈x*,u′〉+〈y*,v′〉=
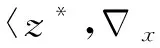
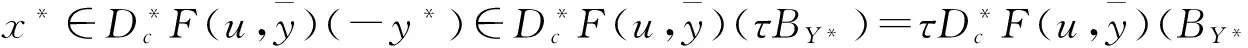
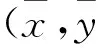
在優(yōu)化中許多問題可歸結(jié)為非線性參數(shù)約束系統(tǒng)的度量次正則性,其中非線性參數(shù)約束系統(tǒng)形如
F(x)={y∈Y|φi(x,y)≤0,ψj(x,y)=0,i=1,…,m;j=1,…,r}.
(6)
其中φi,ψj:X×Y→R為實(shí)值函數(shù)[2].我們給出該系統(tǒng)具有度量次正則性的一個充分條件.
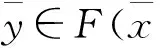
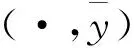
Θ∶={(α1,…,αm,β1,…,βr)|αi≤0,βj=0,i=1,…,m;j=1,…,r},
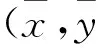
[1] HENRION R,OUTRATA J.Calmness of constraint systems with applications [J].J Math Program,2005,104: 437-464.
[2] MORDUKHOVICH B S.Variational analysis and generalized differentiation Ⅰ,Ⅱ: basic theory [M].New York: Springer-verlag,2006: 23-168.
[3] HELMUT G.First order and second order characterization of metric subregularity and calmness of constraint set mappings [J].SIAM J Optim,2011,4: 1439-1474.
[4] HE Q H,YANG J,ZHANG B B.Metric subregularity for subsmooth generalized constraint equations in Banach spaces [J/OL].J Applied Mathematics,2012[2014-04-02].http://www.hindawi.com/journals/jam/2012/185249.
[5] CLARKE F H.Optimization and nonsmooth analysis [M].New York: Wiley,1983: 46-102.
[6] ZHENG X Y,YANG X Q.Weak sharp minima for semi-infinite optimization problems with applications [J].SIAM J Optim,2007,18: 573-588.
[7] ZHENG X Y,NG K F. Linear regularity for a collection of subsmooth sets in banach spaces [J].SIAM J Optim,2008,19:62-76.
[8] ZHENG X Y,NG K F.Calmness for L-subsmooth multifunctions in banach spaces [J].SIAM J Optim,2009,4: 1648-1673.
[9] 程亞煥,段麗芬,左明霞.賦廣義 Orlicz 范數(shù) Orlicz 函數(shù)空間的完全k-凸性 [J].東北師大學(xué)報(bào)(自然科學(xué)版),2015,47(2):5-8.
[10] 王慧勤,雷 剛.預(yù)條件下含參數(shù)的 JOR 迭代法斂散性分析 [J].東北師大學(xué)報(bào)(自然科學(xué)版),2015,47(1):43-47.
(責(zé)任編輯:李亞軍)
The metric subregularity of parametric constraint systems
ZHANG Bin-bin1,WANG Chuan-jian1,JIN Qiao-hua2
(1.School of Science,Kunming University of Science and Technology,Kunming 650500,China;2.Department of Information Science and Technology,Tourism and Culture College of Yunnan University,Lijiang 674100,China)
Using variational technique,a sufficient condition via Clarke normal cones for metric subregularity of parametric constraint systems is provided.Consequently,a sufficient condition is given for parametric constraint systems of nonlinear programming.
strict differentiability; Clarke normal cone; metrically subregular; parametric constraint systems
1000-1832(2015)04-0046-03
10.16163/j.cnki.22-1123/n.2015.04.010
2014-04-02
國家自然科學(xué)基金資助項(xiàng)目(11261024).
張彬彬(1987—),男,碩士,講師,主要從事非光滑優(yōu)化理論及應(yīng)用研究.
O 177.92 [學(xué)科代碼] 110·57
A

