非余分裂的弱余分裂李代數

夏利猛，白蓮花，張遠嬌

(江蘇大學理學院數學系，江蘇 鎮江 212013)

非余分裂的弱余分裂李代數

夏利猛，白蓮花，張遠嬌

(江蘇大學理學院數學系，江蘇 鎮江 212013)

證明了復數域C上的五維李代數L=sl2+M不是余分裂李代數，從而證明了弱余分裂李代數不一定是余分裂李代數.

余分裂；弱余分裂；非半單李代數

文獻[1]中介紹了一種新的“李代數—李余代數”結構，稱為余分裂李代數，即一個李代數(L，μ)，使得μ°δ等于恒等變換.當μ°δ在某組基下為非退化對角變換時，稱(L，μ，δ)是一個弱余分裂李代數.

定義1[1]一個余分裂李代數是指在一個F-向量空間L上賦予兩個F-線性映射μ：L?FL→L和δ：L→L?FL，使得下列條件成立：

(1) (L，μ)是一個李代數；

(2) (L，δ)是一個李余代數；

(3)μ°δ=idL.

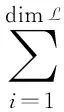
顯然，任意的(弱)余分裂李代數L一定滿足條件[L，L]=L.文獻[3]證明了復數域上任意有限維李代數L=[L，L]一定是一個弱余分裂李代數，反之亦然，并給出了特征域上的一類非半單余分裂李代數的例子.文獻[4-6]中也對余分裂李代數的相關內容做了研究.文獻[7]給出了如下猜想：設L是一個復數域C上的有限維李代數，則L是余分裂的當且僅當L是半單的.并且文獻[7]中證明了復數域C上的有限維李代數是一個內余分裂李代數，當且僅當它是半單的.特別地，它的內余分裂結構是唯一的.

本文主要證明了以下結論：

定理1 李代數L=S+M不是余分裂李代數，其中S是三維單李代數，根基M是S的二維不可約表示，且[M，M]=0.

由文獻[3]中結果可知L是弱余分裂的，從而證明了弱余分裂不一定余分裂.這一證明過程也將有助于對上述猜想的研究.

1 預備知識

設李代數L=sl2+M，其中sl2=span{x,y,h}是三維單李代數，M=span{u,v}是sl2的二維不可約表示.李代數運算為：

[x,y]=h,[h,x]=2x,[h,y]=-2y，[h,u]=u,[h,v]=-v，

[x,v]=u,[y,u]=v,[x,u]=[y,v]=[u,v]=0.

假設L是余分裂李代數，我們用反證法證明其主要結構.由余分裂李代數的定義以及L的結構，不妨設L的余乘法為：

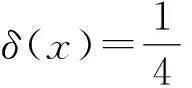
a3(x?v-v?x-h?u+u?h)+a4(y?u-u?y+h?v-v?h)+a5(u?v-v?u)，

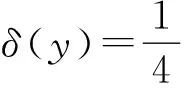
b3(x?v-v?x-h?u+u?h)+b4(y?u-u?y+h?v-v?h)+b5(u?v-v?u)，

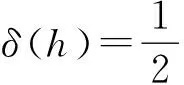
c3(x?v-v?x-h?u+u?h)+c4(y?u-u?y+h?v-v?h)+c5(u?v-v?u)，

δ(u)=d1(h?u-u?h)+d2(x?u-v?x)+d3(u?v-v?u)+d4(x?u-u?x)+

d5(y?v-v?y)+d6(h?v-v?h+y?u-u?y)，

δ(v)=e1(v?h-h?v)+e2(y?u-u?y)+e3(u?v-v?u)+e4(x?u-u?x)+

e5(y?v-v?y)+e6(h?u-u?h-x?v+v?x).

其中

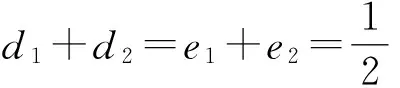
令A=(1?δ)°δ(u)，由δ的定義可知

A=d1[(h?δ(u)-u?δ(h)]+d2[x?δ(v)-v?δ(x)]+d3[u?δ(v)-v?δ(u)]+

d4[x?δ(u)-u?δ(x)]+d5[y?δ(v)-v?δ(y)]+d6[h?δ(v)-v?δ(h)+y?δ(u)-u?δ(y)]=

d1d1h?h?u-d1d1h?u?h+d1d2h?x?v-d1d2h?v?x+d1d3h?u?v-

d1d3h?v?u+d1d4h?x?u-d1d4h?u?x+d1d5h?y?v-d1d5h?v?y+

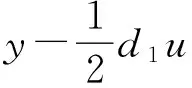
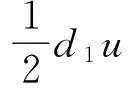
d1c3u?x?v+d1c3u?v?x+d1c3u?h?u-d1c3u?u?h-d1c4u?y?u+

d1c4u?u?y-d1c4u?h?v+d1c4u?v?h-d1c5u?u?v+d1c5u?v?u+

d2e1x?v?h-d2e1x?h?v+d2e2x?y?u-d2e2x?u?y+d2e3x?u?v-

d2e3x?v?u+d2e4x?x?u-d2e4x?u?x+d2e5x?y?v-d2e5x?v?y+

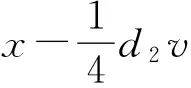
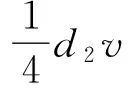
d2a3v?x?v+d2a3v?v?x+d2a3v?h?u-d2a3v?u?h-d2a4v?y?u+

d2a4v?u?y-d2a4v?h?v+d2a4v?v?h-d2a5v?u?v+d2a5v?v?u+

d3e1u?v?h-d3e1u?h?v+d3e2u?y?u-d3e2u?u?y+d3e3u?u?v-

d3e3u?v?u+d3e4u?x?u-d3e4u?u?x+d3e5u?y?v-dd1v?h?u+

d3e6u?h?u-d3e6u?u?h-d3e6u?x?v+d3e6u?v?x-d3d1v?h?u+

d3d1v?u?h-d3d2v?x?v+d3d2v?v?x-d3d3v?u?v+d3d3v?v?u-

d3d4v?x?u+d3d4v?u?x-d3d5v?y?v+d3d5v?v?y-d3d6v?h?v+

d3d6v?v?h-d3d6v?y?u+d3d6v?u?y+d4d1x?h?u-d4d1x?u?h+

d4d2x?x?v-d4d2x?v?x+d4d3x?u?v-d4d3x?v?u+d4d4x?x?u-

d4d4x?u?x+d4d5x?y?v-d4d5x?v?y+d4d6x?y?u-d4d6x?u?y+

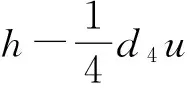
d4a1u?u?x-d4a2u?y?v+d4a2u?v?y-d4a3u?x?v+d4a3u?v?x+

d4a3u?h?u-d4a3u?u?h-d4a4u?y?u+d4a4u?u?y-d4a4u?h?v+

d4a4u?v?h-d4a5u?u?v+d4a5u?v?u+d5e1y?v?h-d5e1y?h?v+

d5e2y?y?u-d5e2y?u?y+d5e3y?u?v-d5e3y?v?u+d5e4y?x?u-

d5e4y?u?x+d5e5y?y?v-d5e5y?v?y+d5e6y?h?u-d5e6y?u?h-

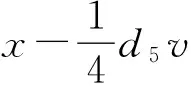
d5b1v?u?x-d5b2v?y?v+d5b2v?v?y-d5b3v?x?v+d5b3v?v?x+

d5b3v?h?u-d5b3v?u?h-d5b4v?y?u+d5b4v?u?y-d5b4v?h?v+

d5b4v?v?h-d5b5v?u?v+d5b5v?v?u+d6e1h?v?h-d6e1h?h?v+

d6e2h?y?u-d6e2h?u?y+d6e3h?u?v-d6e3h?v?u+d6e4h?x?u-

d6e4h?u?x+d6e5h?y?v-d6e5h?v?y+d6e6h?h?u-d6e6h?u?h-

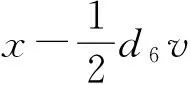
d6c1v?u?x-d6c2v?y?v+d6c2v?v?y-d6c3v?x?v+d6c4v?v?x+

d6c3v?h?u-d6c3v?u?h-d6c4v?y?u+d6c4v?u?y-d6c4v?h?v+

d6c4v?v?h-d6c5v?u?v+d6c5v?v?u+d6d1y?h?u-d6d1y?u?h+

d6d2y?x?v-d6d2y?v?x+d6d3y?u?v-d6d3y?v?u+d6d4y?x?u-

d6d4y?u?x+d6d5y?y?v-d6d5y?v?y+d6d6y?y?u-d6d6y?u?y+

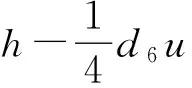
d6b1u?u?x-d6b2u?y?v+d6b2u?v?y-d6b3u?x?v+d6b3u?v?x+

d6b3u?h?u-d6b3u?u?h-d6b4u?y?u+d6b4u?u?y-d6b4u?h?v+

d6b4u?v?h-d6b5u?u?v+d6b5u?v?u.

2 主要結果證明

由余分裂李代數上的Jacobi恒等式(1+ξ+ξ2)°(1?δ)°δ=0，得(1+ξ+ξ2)°(1?δ)°δ(u)=0.從而

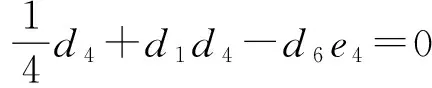
(1)

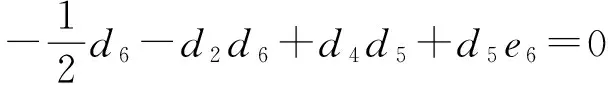
(2)

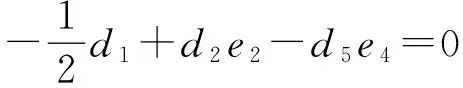
(3)

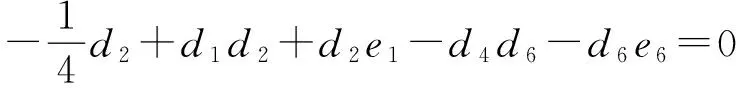
(4)

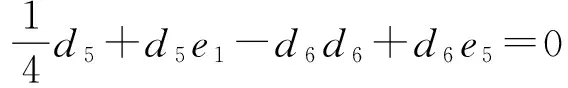
(5)

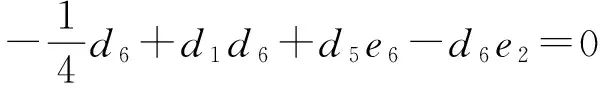
(6)

同理，由(1+ξ+ξ2)°(1?δ)°δ(v)=0，可以得到

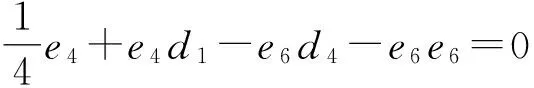
(7)

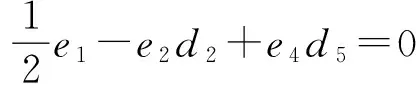
(8)

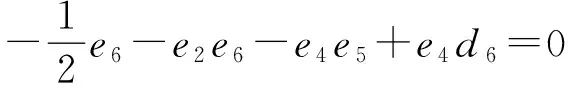
(9)

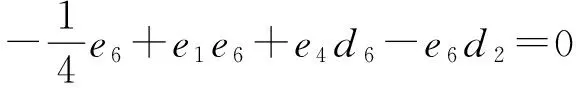
(10)

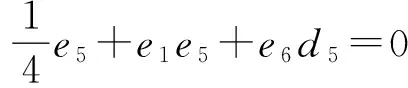
(11)

現在對上述結果做如下討論：

第一種情況，d6≠0.此時由(3)加(8)式得

e1=d1，e2=d2.

(12)

再由(1)式，

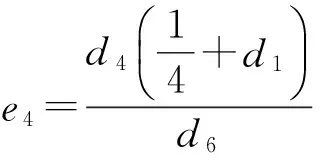
(13)

把(12)，(13)式帶入(3)式有

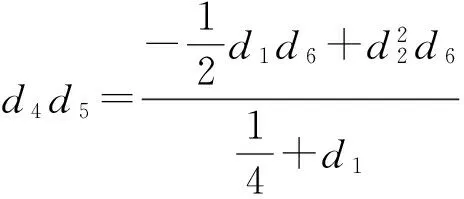
(14)

(2)減(6)式得

(15)

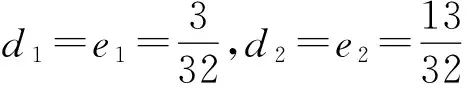
(16)

由此(3)式中

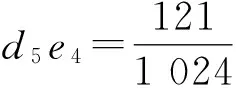
(17)

第二種情況，d6=0.此時由(4)式得

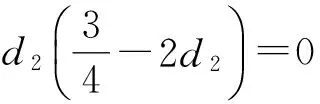
(18)

若d2≠0，有

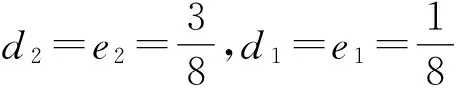
(19)

因此(3)式中，

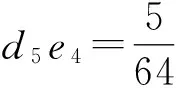
(20)

但由(5)式可得d5=0，這與(2)式矛盾.

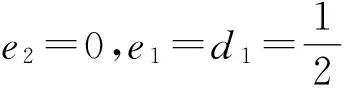
[1] XIA LIMENG，HU NAIHONG.Introduction to co-split Lie algebras[J].Algebra and Representation Theory，2011，14：191-199.

[2] FARNSTEINER R.Lie algebras with a co-algebra splitting[J].Algebra Representation Theory，2011，14：87-96.

[3] XIA LIMENG.Note on co-split Lie algebras[J].Chinese Annals Mathematics，2012，33B(5)：651-656.

[4] 沈彩霞，夏利猛.一類Cartan型余分裂李代數的例子[J].東北師大學報(自然科學版)，2010，42(3)：17-20.

[5] 夏利猛，沈彩霞.具有非退化Killing型的余分裂李超代數[J].東北師大學報(自然科學版)，2009，41(4)：9-12.

[6] 夏利猛，胡乃紅.A(m,n)型余分裂李超代數[J].數學年刊，2008，29(6)：1-4.

[7] 沈彩霞.內余分裂李代數的唯一性[J].東北師大學報(自然科學版)，2015，47(3)：40-43.

(責任編輯：李亞軍)

A weak co-split Lie algebra without co-split structure

XIA Li-meng，BAI Lian-hua，ZHANG Yuan-jiao

(Faculty of Science，Jiangsu University，Zhenjiang 212013，China)

It is proved that 5-dimensional Lie algebraL=sl2+Mis not a co-split Lie algebra.Therefore，a weak co-split Lie algebra is not always a co-split Lie algebra.

co-split；weak co-split；non semi-simple Lie algebra

1000-1832(2015)04-0018-04

10.16163/j.cnki.22-1123/n.2015.04.004

2014-03-24

國家自然科學基金資助項目(11271131).

夏利猛(1976—)，男，博士，副教授，主要從事李代數研究.

O 152.5 [學科代碼] 110·2125

A