基于CFD的離心分離機內(nèi)流場的模擬仿真

霍秋爽， 劉加光， 鄧龍虎， 陳登科

（1.煙臺大學機電汽車工程學院，山東 煙臺 264000；2.清華大學機械工程系，北京 100084）

離心分離（centrifugal separation）是借助于離心力，使比重不同的物質(zhì)進行分離的方法。利用離心分離方法設計的離心機有相當高的轉(zhuǎn)速，離心機內(nèi)被分離物質(zhì)由旋轉(zhuǎn)軸的旋轉(zhuǎn)受到離心力，若被分離物質(zhì)比重不同，則被分離物質(zhì)受到的離心力不同，運動速度及軌跡不同，由此比重不同的物質(zhì)就能夠分離。不同的生物分子有不同的體積和密度，離心分離是分離生物分子最常用的分離方法［1］。隨著生命科學技術(shù)的發(fā)展，離心分離技術(shù)已成為生物化學與分子生物學中不可缺少的分離技術(shù)手段。然而，目前關(guān)于離心分離機的基礎(chǔ)研究相對較少。由于離心分離機內(nèi)部復雜的紊流流動，內(nèi)部流場的可靠數(shù)據(jù)很難通過普通的實驗獲得。近年來，隨著計算機性能及CFD（Computational Fl uid Dynamics）技術(shù)的快速發(fā)展，使用CFD方法計算模擬離心分離機內(nèi)內(nèi)部流場越來越精確。

本文正是采用CFD商業(yè)軟件Fl uent，對離心分離機內(nèi)部流場進行數(shù)值模擬，仿真中液相采用了RNG k－ε湍流模型，固相采用拉格朗日離散相模型（DPM）。通過一定的簡化后建立了離心機模型，利用Solid works軟件取出離心機內(nèi)流體區(qū)域，考察了固相顆粒在流體區(qū)域內(nèi)的分布情況，以及轉(zhuǎn)速對固相顆粒速度的影響。采用CFD方法所得到的離心機內(nèi)部流場的信息，對離心機的研究及設計具有較重要的參考價值。

1 流體動力學（CFD）技術(shù)

離心機內(nèi)部的流場難以直接測量，對于內(nèi)部流場的研究采用計算流體力學（CFD）技術(shù)。計算流體力學（Computational Fluid Dynamics，簡稱 CFD）是以數(shù)值離散方法為數(shù)學基礎(chǔ)，借助于計算機求解描述流體運動的基本方程，研究流體運動規(guī)律的學科。CFD的基本思想是把原來在時間域及空間域上連續(xù)的物理量的場，如速度場和壓力場，用一系列有限個離散點上的變量值的集合來代替，通過一定的原則和方式建立起關(guān)于這些離散點上場變量之間關(guān)系的代數(shù)方程組，然后求解代數(shù)方程組獲得場變量的近似值［2－5］。CFD 可以看做是在流動基本方程（質(zhì)量守恒方程、動量守恒方程、能量守恒方程）控制下對流動的數(shù)值模擬。通過這些模擬，可以得到極其復雜問題的流場內(nèi)各個位置上的基本物理量（如速度、壓力、溫度、濃度等）的分布，以及這些物理量隨時間的變化情況［6－8］。

CFD技術(shù)的特點有：給出流體運動區(qū)域內(nèi)的離散解，而不是解析解；它的發(fā)展與計算機技術(shù)的發(fā)展直接相關(guān)；若物理問題的數(shù)學提法（包括數(shù)學方程及其相應的邊界條件）是正確的，則可在較廣泛的流動參數(shù)（如馬赫數(shù)、雷諾數(shù)、飛行高度、氣體性質(zhì)、模型尺度等）范圍內(nèi)研究流體力學問題，且能給出流場參數(shù)的定量結(jié)果［9］。

2 數(shù)值仿真

2.1 數(shù)值模型選擇

本文研究的對象為固液兩相流，利用軟件FLUENT進行仿真。仿真中，離心分離機中離心腔內(nèi)流體在轉(zhuǎn)動軸帶動下，固相顆粒隨之運動，忽略熱效應的影響，離心機內(nèi)部流體遵循質(zhì)量守恒和動量守恒。本模型數(shù)值仿真中，用純水代替液相，利用拉格朗日方程計算固相顆粒運動軌跡，研究對象采用RNG k－ε湍流模型，這種模型與標準k－ε湍流相似，但RNG k－ε湍流模型能模擬的范圍更廣，結(jié)果更精確［10］。這是由于RNG k－ε的方程中出現(xiàn)了新的函數(shù)項，得到的湍動能和耗散率方程為［11－14］：

采用DPM模型來跟蹤固相顆運動，固相顆粒的作用力平衡方程在笛卡爾坐標系下的形式為：

式中，F(xiàn)D（u－up）為顆粒的單位質(zhì)量曳力，μp為液相速度，up為顆粒速度，μp為流體動力黏度，η為流體密度，pp為顆粒密度，gx為顆粒受到的其他加速度，F(xiàn)x為其他作用力。

2.2 數(shù)值模型的建立

1）利用三維建模軟件UG，建立離心機理想模型。如圖1所示，該模型工作原理，混合液進入離心腔，旋轉(zhuǎn)軸在電動機的帶動下，以一定的轉(zhuǎn)速旋轉(zhuǎn)，旋轉(zhuǎn)軸帶動混合液，使液體加速旋轉(zhuǎn)，在液固的相互作用下，固相顆粒也被帶動，有一定的速度。

2）將模型導入Solid Works內(nèi)，通過型腔等命令，提取離心機內(nèi)部流場。將提取后的內(nèi)部流場，保存為fl uent.x＿t。

3）將fl uent.x＿t導入進ICEM中劃分網(wǎng)格，結(jié)果如圖2所示.劃分好網(wǎng)格后，將網(wǎng)格文件保存為.mesh文件，導入FLIENT14.5進行仿真。

圖1 離心分離簡化圖

圖2 離心分離機網(wǎng)格劃分圖

2.3 材料物性、邊界條件和初始條件

1）離心腔模擬仿真中，水溫為20℃，此時水的密度為P＝998.2 kg／m2，黏度為μ＝1.005 cp；固相粒子材料設置為wood，直徑為5×10－12m，流量為6.87×10－12kg／s，在流體區(qū)域初始的位置坐標為（x，y，z）＝（0.06 m，0.06 m，0.02 m）。

2）固相顆粒的初始速度為零；離心分離轉(zhuǎn)軸轉(zhuǎn)速為2 000 r／min、4 000 r／min、6 000 r／min；不設置液固相進出口。所選模型為DPM型，湍流模型選擇RNG k－ε湍流模型。

3）求解，選用穩(wěn)態(tài)求解：連續(xù)性方程、動量方程、湍動能方程和湍動能耗方程均采用二階迎風格式離散計算，各物理殘差均下降至1×10－4；為了避免非線性問題的發(fā)散，采用欠松弛迭代的方法［15－19］。

4）分別改變固相顆粒密度及旋轉(zhuǎn)軸轉(zhuǎn)速進行仿真運行。

3 仿真結(jié)果及分析

仿真中旋轉(zhuǎn)軸轉(zhuǎn)速為2 000 r／min，不同的固相顆粒在X-Y平面上運動軌跡及速度如圖3所示，圖中有顏色曲線為固相顆粒在X-Y平面上的運動軌跡，不同顏色帶表著固相顆粒不同的的運動速度。圖4以及下頁圖5旋轉(zhuǎn)軸轉(zhuǎn)速為4 000 r／min、6 000 r／min時不同的固相顆粒在X-Y平面上運動軌跡及速度分布圖。

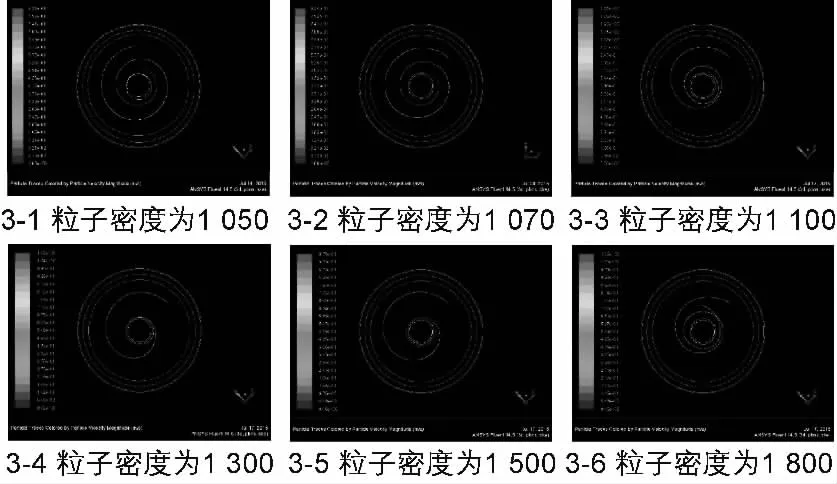
圖3 不同密度的固相顆粒在X-Y平面上運動軌跡及速度圖旋轉(zhuǎn)軸轉(zhuǎn)速為2 000 r／min（kg／m3）

圖4 不同密度的固相顆粒在X-Y平面上運動軌跡及速度圖旋轉(zhuǎn)軸轉(zhuǎn)速為4 000 r／min（kg／m3）

圖5 不同密度的固相顆粒在X-Y平面上運動軌跡及速度圖旋轉(zhuǎn)軸轉(zhuǎn)速為6 000 r／min（kg／m3）

如上圖3、圖4、圖5所示，從同一位置（0.06 m，0.06 m，0.02 m）釋放的固相顆粒，顆粒密度、旋轉(zhuǎn)軸速度不同，固相顆粒的運動軌跡不同。對比同一旋轉(zhuǎn)轉(zhuǎn)速下，可知顆粒密度不同，經(jīng)一定時間解算后固相顆粒所在位置不同，顆粒的速度也不同。

經(jīng)過研究發(fā)現(xiàn)：在相同的旋轉(zhuǎn)軸轉(zhuǎn)速下，在同一位置釋放固相顆粒，顆粒的位置在不斷變化，例如在旋轉(zhuǎn)軸轉(zhuǎn)速為2 000 r／min，固相相顆粒密度從1 050增加到1 800，由圖知顆粒的位置到旋轉(zhuǎn)軸中心的距離在變小；在旋轉(zhuǎn)軸轉(zhuǎn)速4 000 r／min，固相顆粒的位置到旋轉(zhuǎn)軸中心的距離隨顆粒的密度增大而變小，隨著粒子的密度增加到一定時，粒子的位置到旋轉(zhuǎn)軸中心的距離變大；在旋轉(zhuǎn)軸轉(zhuǎn)速6 000 r／min時，隨著粒子密度增加，粒子的位置到旋轉(zhuǎn)軸中心的距離變小，但隨著粒子的密度增加到一定量時，粒子的位置到旋轉(zhuǎn)軸中心的距離漸漸增大。

而對比上述圖3、圖4、圖5中固相顆粒為密度為1 050時，固相顆粒的速度有很明顯的變化趨勢，如圖6所示。

圖6 固相顆粒的速度大小圖（密度為1 050）

圖中橫坐標是仿真的響應時間，縱坐標為 固相顆粒的速度；不同曲線走勢代表不同旋轉(zhuǎn)軸轉(zhuǎn)速下，固相顆粒在Fl uent軟件中達到穩(wěn)態(tài)之后隨響應時間的變化。當旋轉(zhuǎn)軸轉(zhuǎn)速為2 000 r／min時，密度為1 050的固相顆粒速度大小為0.477 m／s，且一直穩(wěn)定的保持在 0.477 m／s上下，不隨迭代次數(shù)的增多而變化。當旋轉(zhuǎn)軸轉(zhuǎn)速不同時，密度相同的固相顆粒的速度的變化規(guī)律相同。

同樣，對比上述圖3、圖4、圖5中固相顆粒為密度為1 070、1 100、1 300、1 500、1 800時的情況，又得到5組相同規(guī)律的數(shù)據(jù)，由上述圖可知旋轉(zhuǎn)軸的轉(zhuǎn)速對固相顆粒速度的大小影響比較大。

4 結(jié)論

本文采用離散相模型對離心分離機內(nèi)的流場進行仿真，由仿真結(jié)果可知：

1）固相顆粒在流體區(qū)域中的速度大小主要由旋轉(zhuǎn)軸轉(zhuǎn)速決定，固相顆粒的速度隨著轉(zhuǎn)速的增大而增大。

2）固相顆粒的位置固定時，旋轉(zhuǎn)軸轉(zhuǎn)速相同時，固相顆粒的密度越大，在FLUENT軟件中經(jīng)過一定時間的解算后，固相顆粒所達到的速度有越來越大的趨勢。

3）顆粒的位置固定時，固體顆粒的密度一定時，粒子所在的位置到旋轉(zhuǎn)中心的距離有變遠的趨勢。

［1］ 金綠松，林元喜等.現(xiàn)代分離科學與技術(shù)叢書—離心分離［M］.北京：化學工業(yè)出版社，2008.

［2］ 楊敏官，王軍鋒，羅惕乾，等.流體機械內(nèi)部流動測量技術(shù)［M］.北京：機械工業(yè)出版社，2006.

［3］ 李亞林，袁壽其，湯躍，等.離心泵內(nèi)流場PIV測試中示蹤粒子跟隨性的計算［J］.排灌機械工程學報，2012，30（1）：12-14

［4］ 王福軍.計算流體動力學分析—CFD軟件原理與應用［M］.北京：清華大學出版社，2004.

［5］ 魏新利，張海紅，王定標，等.旋風分離器內(nèi)顆粒軌跡的數(shù)值模擬［J］.鄭州大學學報（工學版），2004，25（3）：14-17，59.

［6］ 馮立成，周密，易澤明.離心機復雜轉(zhuǎn)鼓的有限元優(yōu)化計算［J］.機械強度，2002（2）：295-297

［7］ 劉瑞韜，徐忠.離心葉輪機械內(nèi)部流動的研究進展［J］.力學進展，2003（4）：518-532.

［8］ 袁建平，袁壽其，何志霞.流場測試技術(shù)及其在離心泵中的應用進展［J］.水泵技術(shù)，2003（2）：10-11

［9］ 楊雪峰.大型空冷汽輪發(fā)電機定子內(nèi)流體場與溫度場計算與分析［D］.哈爾濱：哈爾濱理工大學，2009.

［10］ 石鑫，向陽，文利雄，陳建峰.基于離散相模型的旋轉(zhuǎn)填充床內(nèi)的流場分析［J］.高校化學工程學報，2012（3）：388-394.

［11］ Tsay J，F(xiàn)ox R D，Ozkan H E，et al.Evaluation of a pneu matic-shield spraying system by CFD simulation［J］.Transactions of the ASAE，2002，45（1）：47-54.

［12］ Delele M A，Moor A De，Sonck B，et al.Modelling and validation of the air flow generated by a cross flow air sprayer as affected by travel speed and fan speed［J］.Biosystems Engineering，2005，92（2）：165-174.

［13］ Adrian R J.Particle-image techniques for experimental fluid mechanics［J］.Annual Review Fluid Mechanics，1991（23）：261-304.

［14］ Adrian R J.Twenty years of paricle image velocimetry［J］.Experiments in Fluids，2005，39（2）：159-169.

［15］ 張金偉.流體機械葉輪內(nèi)部流場測試技術(shù)進展［J］.科技與企業(yè)，2013（4）：308.

［16］ 范強，李永杰.旋轉(zhuǎn)旋流離心機轉(zhuǎn)鼓內(nèi)流體動力學研究［J］.機械研究與應用，2009（4）：47-49.

［17］ 范強，孟坤六，梅云新，閻國珍，甘大才.旋轉(zhuǎn)旋流離心機轉(zhuǎn)鼓內(nèi)流場分析［J］.西南石油學院學報，1997（4）：7-8，90-94.

［18］ 陳愛華.旋轉(zhuǎn)旋流分離機運動合成和結(jié)構(gòu)研究［D］.浙江工業(yè)大學，2007

［19］ 孫國祥，汪小旵，丁為民，等.基于CFD離散相模型霧滴沉積特性的模擬分析［J］.農(nóng)業(yè)工程學報，2012（6）：13-19.