基于有限元分析的高頻輪軌力研究

王晶 陳建政

摘 要：測力輪對是目前最有效的輪軌力測量方法。根據國標要求，測力輪對最高測量頻率為90Hz。由于在實際運行中，如果車輪受到與共振頻率相同頻率的激勵時，很可能會產生模態共振，對輪軌力的測量產生很大的影響。文章采用頻率為1-3000Hz的掃頻激勵對車輪進行諧響應分析。設計補償濾波器，對固有頻率處產生的共振峰值進行補償。

關鍵詞：高頻輪軌力；模態；諧響應分析；濾波器

輪軌之間的作用力（簡稱輪軌力）是評判鐵道車輛運行安全性和穩定性的重要參數。測力輪對作為目前測量輪軌力最直接最準確的方法。它的測量原理主要是以輪對作為輪軌力的檢測傳感器，通過測量車輪輻板有限點處的應變實現輪軌接觸力的連續檢測。能否精確地獲取輪軌間的作用力直接影響著蠕滑、波磨及脫軌等的計算。

在實際的列車運行中，車輪所受的輪對力是一段從低頻到高頻的廣譜。根據模態振動理論，當車輪在某些特定的頻率處激勵時，會引發模態共振。根據UIC518標準，測力輪對最高測量頻率是90Hz，而根據文章仿真結果，輪對的一階共振頻率為159Hz，如果軌道激勵中包含一階或更高階共振頻率，則不可避免的將共振信號疊加到腹板應變上，造成很大的測量誤差[1]。

對高頻輪軌力的研究，首先對車輪有限元模型進行模態分析，然后對模型進行諧響應分析，求解出車輪應變響應。在應變響應中，各階固有頻率處會產生共振峰值，設計FIR數字濾波器，對頻響曲線進行補償濾波。

1 ANSYS有限元模型的建立及分析

在ansys中建立車輪三維模型，設置材料參數：楊氏模量E=2.1E11Pa，泊松比為0.3。單元類型的選擇主要考慮結構的受力特性，選擇的原則是對所選的單元可以使計算精度高、收斂速度快、計算量小模型網格劃分采用的單元是六面體八節點實體單元Solid185，因為本論文分析的重點是輪輻處的應變，所以這一部分的單元劃分密集一些，為了減少單元數，提高計算速度，對于其它部分的網格劃分相對疏一些。在車輪內徑施加全約束，防止車輪做平動和轉動。建好的車輪有限元模型如圖1所示。

圖1 車輪有限元模型

2 模態計算及分析

模態分析用于確定車輪的振動特性，即結構的固有頻率和振型。為獲得車輪的固有屬性，計算模態采用分塊Lanczos法，提取車輪17階模態，計算結果列于模態分析的基本思想是由于結構的模態密集而且相互耦合，應用物理分離模態技術難于獲得模態參數，通過描述結構的動態性能矩陣方程解耦，從而可以使N 自由度的動力學特性用單自由度系統表示。其核心內容是確定用以描述結構系統特性的固有頻率，阻尼比和振型等模態參數。計算模態分析從結構特性與材料特性等原始參數出發，采用有限元法形成系統的離散數學模型——質量矩陣和剛度矩陣，然后通過求解特征值的問題，確定系統的模態參數。由模態迭加法，可以分析結構在已知外載荷作用下的動態響應或穩定性問題。求解出車輪振型圖提取前4階如圖2所示。

3 諧響應分析

任何作用在結構系統上持續的周期載荷都將在結構系統中產生持續的諧響應。諧響應分析是用于確定線性結構在承受隨時間按簡諧規律變化的載荷時穩態響應的技術，為了獲得車輪在固有頻率處實際的各類響應值，對模態分析后的車輪進行諧響應分析。

系統的動態特性可以用沖擊響應函數h（t）來描述。t（h）的定義為任意時刻上系統對單位沖擊輸入的響應，則對任意輸入x（t），系統的輸出y（t）為

（3-1）

對上式兩邊去傅里葉變換，令X（？棕）是x（t）的傅里葉變換，Y（？棕）是響應輸出y（t）的傅里葉變換，則可以得到響應函數的表達式為

（3-2）

式中， 為幅頻特性；

為相頻特性。

頻率響應函數就是系統的幅頻和相頻特性。如果假定輸入是頻率為？棕的正弦波，輸出也是一個相同頻率的波。同一頻率的輸出振幅值比，等于系統的模|H（？棕）|；輸出和輸入的相位差等于系統的相角？準（？棕）[3]。

圖3 應變頻響曲線

若輸入信號x（t）為單位階躍信號，則進行傅里葉變化X（？棕）=1，H（？棕）=Y（？棕），則系統的輸出響應的傅里葉變化即為系統的傳遞函數。文章設計的諧響應載荷輸入為幅值恒定為1N，頻率為1-3000Hz，經過計算求解出車輪應變的幅頻和相頻響應函數，由幅頻響應曲線可知幅頻響應中對應固有頻率處會產生共振峰值。截取一段車輪上某個節點的應變頻響曲線如圖3所示。

4 FIR數字濾波器的設計

濾波器的作用是對輸入信號起到濾波的作用。文章采用頻率采樣法設計FIR濾波器，濾掉共振頻率下的共振峰值。

頻率抽樣法則是從頻域出發，把給定的理想頻率響應Hd（ej？棕）加以等間隔抽樣得到Hd（k）即：

（4-1）

然后以此Hd（k）作為實際FIR濾波器的頻率特性的抽樣值H（k），即

（4-2）

根據Hd（k），由DFT定義可唯一確定有限長序列H（k），即：

（4-3）

根據采樣定理，可以由頻率響應函數在[0，2？仔]上的N點進行間隔采樣利用這N個頻域抽樣值H（k），同樣利用頻率內插公式可得FIR濾波器的系統函數H（z），即：

圖4 頻率采樣法設計流程

頻率采樣法內插公式： （4-4）

在抽樣點之間存在一定的逼近誤差。誤差大小取決于理想頻率響應的曲線形狀，曲線變化越平緩，則內插值越接近理想值，逼近誤差越小[4]。具體設計步驟流程如圖4所示。

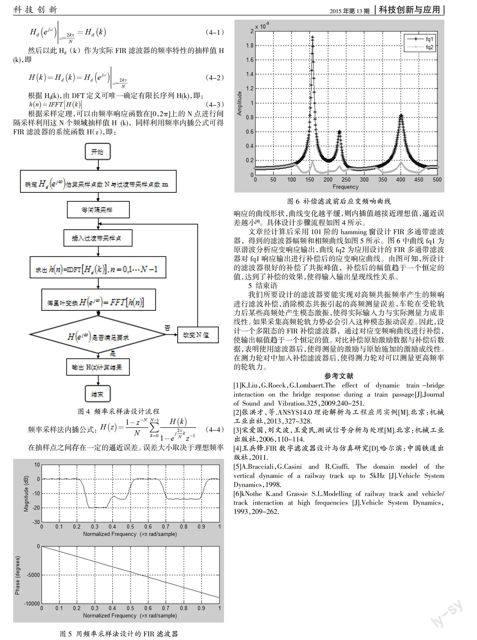
文章經計算后采用101階的hamming窗設計FIR多通帶濾波器，得到的濾波器幅頻和相頻曲線如圖5所示。圖6中曲線fq1為原諧波分析應變響應輸出，曲線fq2為應用設計的FIR多通帶濾波器對fq1響應輸出進行補償后的應變響應曲線。由圖可知，所設計的濾波器很好的補償了共振峰值，補償后的幅值趨于一個恒定的值，達到了補償的效果，使得輸入輸出呈現線性關系。

5 結束語

我們所要設計的濾波器要能實現對高頻共振頻率產生的頻響進行濾波補償，消除模態共振引起的高頻測量誤差，車輪在受輪軌力后某些高頻處產生模態激振，使得實際輸入力與實際測量力成非線性。如果采集高頻輪軌力勢必會引入這種模態振動誤差。因此，設計一個多阻態的FIR補償濾波器，通過對應變頻響曲線進行補償，使輸出幅值趨于一個恒定的值。對比補償原始激勵數據與補償后數據，表明使用濾波器后，使得測量的激勵與原始施加的激勵成線性。在測力輪對中加入補償濾波器后，使得測力輪對可以測量更高頻率的輪軌力。

參考文獻

[1]K.Liu，G.Roeck，G.Lombaert.The effect of dynamic train-bridge interaction on the bridge response during a train passage[J].Journal of Sound and Vibration.325，2009.240-251.

[2]張洪才，等.ANSYS14.0理論解析與工程應用實例[M].北京：機械工業出社，2013，327-328.

[3]宋愛國，劉文波，王愛民.測試信號分析與處理[M].北京：機械工業出版社，2006，110-114.

[4]王兵鋒.FIR數字濾波器設計與仿真研究[D].哈爾濱：中國鐵道出版社，2011.

[5]A.Bracciali，G.Casini and R.Ciuffi. The domain model of the vertical dynamic of a railway track up to 5kHz[J].Vehicle System Dynamics，1998.

[6]kNothe K.and Grassie S.L.Modelling of railway track and vehicle/track interaction at high frequencies[J].Vehicle System Dynamics，1993，209-262.