偶特征有限域上一類高斯正規(guī)基的對(duì)偶基及跡基

李雪連, 廖群英(四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)

?

偶特征有限域上一類高斯正規(guī)基的對(duì)偶基及跡基

李雪連, 廖群英*
(四川師范大學(xué) 數(shù)學(xué)與軟件科學(xué)學(xué)院, 四川 成都 610066)

設(shè)q為2的方冪,文獻(xiàn)(李波,廖群英. 數(shù)學(xué)進(jìn)展,2015,44(3):394-404.)確定了Fqn在Fq上的一類特殊的高斯正規(guī)基及其對(duì)偶基的生成元.進(jìn)一步完全確定了這類正規(guī)基的對(duì)偶基及跡基的乘法表和復(fù)雜度,從而完善了主要結(jié)果.并證明了這類正規(guī)基的跡基是最優(yōu)正規(guī)基.

有限域; 高斯正規(guī)基; 對(duì)偶基; 跡正規(guī)基; 乘法表; 復(fù)雜度

1 引言和主要結(jié)果

設(shè)q為素?cái)?shù)p的方冪,n是正整數(shù),Fqn是有限域Fq的n次擴(kuò)張(n≥2),若

N={α,αq,…,αqn-1}

為Fqn在Fq上的一組正規(guī)基,則稱α為Fqn在Fq上的一個(gè)正規(guī)元.進(jìn)而令

則T=(ti,j)n×n為N的乘法表,T中非零元素的個(gè)數(shù)稱為N的復(fù)雜度,記為CN.由于T=(ti,j)中的非零元越少,Fqn中乘法運(yùn)算的計(jì)算量也就越小,所以尋找低復(fù)雜度的正規(guī)基是一個(gè)很重要的課題.R. Mullin等[1]證明了CN≥(2n-1).且當(dāng)CN=(2n-1)時(shí),稱N為最優(yōu)正規(guī)基,進(jìn)而給出了兩類最優(yōu)正規(guī)基的構(gòu)造定理,分別為Ⅰ型最優(yōu)正規(guī)基和Ⅱ型最優(yōu)正規(guī)基,并猜想最優(yōu)正規(guī)基只有這2類.隨后,S. Gao等[2-3]證明了這個(gè)猜想.從而尋找次優(yōu)的正規(guī)基也成了很重要的課題.1990年,A. Wassermann[4]把最優(yōu)正規(guī)基推廣到高斯正規(guī)基,而這正是一類低復(fù)雜度的正規(guī)基.

k-型高斯正規(guī)基的構(gòu)造定理[4]設(shè)q為素?cái)?shù)p的方冪,k和n是正整數(shù),滿足kn+1是素?cái)?shù)且(kn+1,p)=1.假定δ∈Fqn是kn+1次本原單位根,s是q模kn+1的次數(shù).若(kn/s,n)=1,l是Zkn+1中k次本原單位根,則

生成Fqn在Fq上的正規(guī)基N,且其復(fù)雜度滿足

稱N為Fqn在Fq上的k-型高斯正規(guī)基.

注 1 當(dāng)k=1時(shí),1-型高斯正規(guī)基即是Ⅰ型最優(yōu)正規(guī)基;當(dāng)q=k=2時(shí),2-型高斯正規(guī)基即是Ⅱ型最優(yōu)正規(guī)基.

2005年,廖群英等[5]給出了有限域Fqn在Fq上Ⅰ型最優(yōu)正規(guī)基和Ⅱ型最優(yōu)正規(guī)基的乘法表;2012年,M. Christopoulou等[6]給出了k=3,4,5,6時(shí),有限域Fqn在Fq上的k-型高斯正規(guī)基的乘法表和復(fù)雜度的準(zhǔn)確公式;廖群英等[7]把文獻(xiàn)[6]的結(jié)果推廣到一般情形,給出了有限域Fqn在Fq上一類k-型高斯正規(guī)基的乘法表和復(fù)雜度的具體計(jì)算公式.

另一方面,在有限域的眾多基中,對(duì)偶基也是一個(gè)很重要的概念.對(duì)于Fqn在Fq上的任意2組基:

B={βi=βqi|i=0,1,…,n-1},

N={αi=αqi|i=0,1,…,n-1},

稱B為N的對(duì)偶基,若對(duì)任意的i,j=0,1,…,n-1,都有

其中

是γ∈Fqn在Fq上的跡映射.文獻(xiàn)[8]證明了有限域上正規(guī)基的存在性,對(duì)偶基的存在唯一性以及正規(guī)基的對(duì)偶基仍為正規(guī)基等.2012年,Q. Y. Liao等[9]給出了高斯正規(guī)基的對(duì)偶基,即證明了如下的結(jié)果:

引理 1.1 設(shè)q為素?cái)?shù)p的方冪,N={α,αq,…,αqn-1}為Fqn在Fq上的k-型高斯正規(guī)基(1≤k≤n),則N的對(duì)偶基的生成元為

眾所周知,在編碼理論、密碼體制等領(lǐng)域,低復(fù)雜度的正規(guī)基得到廣泛應(yīng)用[10-12].例如,域F2上元素乘法是實(shí)現(xiàn)橢圓曲線公鑰密碼體制(ECC)的核心運(yùn)算.由文獻(xiàn)[13]可知有限域上的正規(guī)基特別是最優(yōu)正規(guī)基更適用于硬件實(shí)現(xiàn),可見尋找低復(fù)雜的正規(guī)基很重要.設(shè)Tr是γ∈F2n在F2上的跡映射,李波等[14]研究了F2n在F2上滿足條件

的高斯正規(guī)基N={αi=αqi|i=0,1,…,n-1}.證明了:當(dāng)n=4,8,16時(shí),N滿足條件P;但當(dāng)n=32時(shí),F2n在F2上不存在滿足條件P的正規(guī)基,并進(jìn)一步給出偶特征有限域上滿足條件P的正規(guī)基的存在性條件,即證明了如下的結(jié)果.

引理 1.2[14]設(shè)n≥k>1,q為2的方冪,N為Fqn在Fq上的k-型高斯正規(guī)基,則

1) 當(dāng)k≡0(mod 2)時(shí),N不滿足條件P.

2) 當(dāng)k≡1(mod 2)時(shí),N滿足條件P當(dāng)且僅當(dāng)n=4且k=1或者k=3.

本文進(jìn)一步研究偶特征有限域上滿足條件P的高斯正規(guī)基,給出了其對(duì)偶基與跡基的乘法表和復(fù)雜度等,即證明了如下主要結(jié)果.

定理 1.3 設(shè)n≥k>1,q為2的方冪,N為Fqn在Fq上滿足條件P的k-型高斯正規(guī)基,B為N的對(duì)偶基,CB為B的復(fù)雜度,則B滿足條件P,且

定理 1.4 設(shè)q為2的方冪,N為Fqn在Fq上滿足條件P的k-型高斯正規(guī)基,M為N的跡正規(guī)基,則M是Fq2在Fq上的最優(yōu)正規(guī)基.

2 主要結(jié)果的證明

為證明定理1.3和1.4,需要如下幾個(gè)引理.

引理 2.1[15]設(shè)q為素?cái)?shù)p的方冪,

N={α,αq,…,αqn-1}

是Fqn在Fq上的k-型高斯正規(guī)基,

是α∈Fqn在Fq上的跡映射,則Tr(α)=-1.

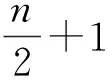
引理 2.3[16]設(shè)q為素?cái)?shù)p的方冪,n是正整數(shù),Fqn是有限域Fq的n次擴(kuò)張(n≥2).若正整數(shù)m為n的因數(shù),且N={α,αq,…,αqn-1}為Fqn在Fq上的正規(guī)基,則

生成Fqm在Fq上的正規(guī)基M={γ,γq,…,γqm-1},稱為N的跡正規(guī)基.

定理1.3的證明 設(shè)N={αi=αqi|i=0,1,2,3}是Fq4在Fq上滿足條件P的k-高斯正規(guī)基,則由引理1.2可知q為2的方冪且k=1或3.設(shè)

B={βi=βqi|i=0,1,2,3}

為N的對(duì)偶基,注意到q為2的方冪且k=1或3,故由引理1.1可得

于是相應(yīng)地有

β1=βq=1+α3,

β2=β1q=1+α0,

β3=β2q=1+α1.

(1)

從而由αi=αqi(i=0,1,2,3)可得

ββ0=(1+α2)2=

1+α2α2=1+(αα0)q2,

(2)

ββ1=(1+α2)(1+α3)=

1+α2+α3+α2α3,

(3)

ββ2=(1+α2)(1+α)=

1+α2+α+α2α,

(4)

ββ3=(1+α2)(1+α1)=

1+α2+α1+α1α2.

(5)

情形一 當(dāng)k=1時(shí),N是Ⅰ型最優(yōu)正規(guī)基,于是由文獻(xiàn)[5]的定理1可知N的乘法表T=(tij)4×4滿足:當(dāng)j=0,1,2,3時(shí),有t2,j=-1;當(dāng)i=0,1,3時(shí),

又由k=1,n=4以及k-型高斯正規(guī)基的構(gòu)造定理可知,q模5的階為4,從而

或

進(jìn)而由q是2的方冪,可知N的乘法表T=(tij)4×4形如

(6)

或

(7)

1) 若N的乘法表為(6)式,則

αα0=α1,αα1=α3,

αα2=α+α1+α2+α3,αα3=α2.

(8)

又由引理2.1知1=Tr(α)=α+α1+α2+α3,其中Tr是Fq4到Fq上的跡映射.從而由(2)～(5)式及(8)式可得

ββ0=1+(αα0)q2=

1+(α1)q2=1+α3=β1,

(9)

ββ1=1+α2+α3+α2α3=

1+α2+α3+α1=β+β1+β3,

(10)

ββ2=1+α2+α+α2α=

1+α1+α3=α+α2=β+β2,

(11)

以及

ββ3=1+α2+α1+α0=β+β2+β3.

(12)

故此時(shí)B的乘法表為

且CB=9.進(jìn)而由引理2.1,以及(1)、(9)～(12)式可知

即B也滿足條件P.

2) 若N的乘法表為(7)式,則

αα0=α3,αα1=α2,

αα2=α+α1+α2+α3,αα3=α1.

(13)

于是由(2)～(5)以及(13)式得到:

ββ0=1+(α3)q2=1+α1=β3,

(14)

ββ1=1+α2+α3+α2α3=

1+α2+α3+α0=β+β1+β2,

(15)

ββ2=1+α2+α+α2α=

1+α2+α+α+α1+α2+α3=

β+β2,

(16)

ββ3=1+α2+α1+α3=β+β1+β3.

(17)

從而相應(yīng)的B的乘法表為

即CB=9.進(jìn)而由引理2.1,以及(1)、(14)～(17)式有

因此B也滿足條件P.綜上可知,CB=9且B也滿足條件P,即定理1.3的第一種情形成立.

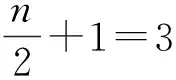
(18)

同理

(19)

和

(20)

以及

(21)

于是由(1)～(5)式可知,相應(yīng)地

(22)

(23)

(24)

注 2 由正規(guī)基的概念可知ββ2=0的情形是不存在的,所以ββ2只可能有以下5種情形

ββ2=1+α2+α+α2α=

(25)

以及

ββ3=1+α2+α1+α1α2=

(26)

于是由正規(guī)基的乘法表及復(fù)雜度的定義可知,B的復(fù)雜度CB滿足

7=2n-1≤CB≤1+3+4+3=11.

又由引理2.1,以及(22)～(23)、(25)～(26)式可得

故此時(shí)B也滿足條件P.這就證明了定理1.3的第二種情形.

定理1.4的證明 由N滿足條件P,及引理1.2知q為2的方冪且n=4,k=1或k=3.于是由引理2.3可知N的跡正規(guī)基M={γ,γq},其中Tr是Fq4到Fq2上的跡映射,且

γ=Tr(α)=α+αq2=α+α2∈Fq2/Fq, (27)

γq=Tr(αq)=αq+αq3=α1+α3∈Fq2/Fq. (28)

情形一 當(dāng)n=4且k=1時(shí),由定理1.3第一種情形的證明,可知有如下2種情形.

1) 當(dāng)N的乘法表為(6)式時(shí),即

αα0=α1,αα1=α3,

αα2=α+α1+α2+α3=1,αα3=α2，

故

γγ=(α+αq2)(α+αq2)=αα+α2α2=

αα+(αα)q2=α1+(α1)q2=α1+α3=γq,

γγq=(α+αq2)(α+αq3)=

αα1+αα3+α1α2+α2α3=

α3+α2+(αα1)q+(αα1)q2=

α3+α2+(α3)q+(α3)q2=

α3+α2+α+α1=γ+γq.

因此M的乘法表

故CM=3.

2) 當(dāng)N的乘法表為(7)式時(shí),類似可得

故CM=3=2×2-1.

綜上可知,當(dāng)n=4,且k=1時(shí),N的跡正規(guī)基M是Fq2在Fq上的最優(yōu)正規(guī)基.

情形二 當(dāng)n=4,k=3時(shí),由(27)～(28)式可知:

γγ=(α+αq2)(α+αq2)=

αα+α2α2=αα+(αα)q2,

γγq=(α+α2)(α1+α3)=

αα1+αα3+α1α2+α2α3=

αα1+αα3+(αα1)q+(αα1)q2.

故γγ,γγq的取值決定于αα,αα1,αα3.而由(18)～(21)式知αα有3種取法,αα1有4種取法,αα3有4種取法,且αα1≠αα3.故有以下22種情形.

情形1:當(dāng)αα=α1,αα1=α+α1+α2,αα3=α+α1+α3時(shí),

γγ=αα+(αα)q2=α1+α3=γq,

γγq=αα1+αα3+(αα1)q+(αα1)q2=

α+α2+α1+α3=γ+γq.

于是

故CM=3.

情形2:當(dāng)αα=α1,αα1=α+α1+α2,αα3=α1+α2+α3時(shí).

情形3:當(dāng)αα=α1,αα1=α+α2+α3,αα3=α1+α2+α3時(shí).

情形4:當(dāng)αα=α1,αα1=α+α1+α3,αα3=α+α2+α3時(shí).

情形5:當(dāng)αα=α1,αα1=α1+α2+α3,αα3=α+α1+α2時(shí).

情形6:當(dāng)αα=α3,αα1=α+α1+α2,αα3=α+α1+α3時(shí).

情形7:當(dāng)αα=α3,αα1=α+α1+α2,αα3=α1+α2+α3時(shí).

情形8:當(dāng)αα=α3,αα1=α+α2+α3,αα3=α1+α2+α3時(shí).

情形9:當(dāng)αα=α3,αα1=α+α1+α3,αα3=α+α2+α3時(shí).類似都可以得到

故CM=3.

情形10:當(dāng)αα=α1,αα1=α+α1+α2,αα3=α+α2+α3時(shí),

γγ=αα+(αα)q2=α1+α3=γq,

γγq=αα1+αα3+(αα1)q+(αα1)q2=

α+α1+α2+α+α2+α3+

α1+α2+α3+α+α2+α3=

α+α3.

又由引理2.1知:α+α2+α1+α3=-1,即γ+γq=-1=1,q≡0(mod2).注意到:(α+α3)q2=α1+α2且α+α3=γγq∈Fq2,于是(α+α3)q2=α+α3,故α1+α2=α+α3,從而α1+α2+α+α3=0,與引理2.1矛盾,故此情形不成立.

情形11:當(dāng)αα=α1,αα1=α+α2+α3,αα3=α+α1+α3時(shí).

情形12:當(dāng)αα=α1,αα1=α+α2+α3,αα3=α+α1+α2時(shí).

情形13:當(dāng)αα=α1,αα1=α+α1+α3,αα3=α+α1+α2時(shí).

情形14:當(dāng)αα=α1,αα1=α+α1+α3,αα3=α1+α2+α3時(shí).

情形15:當(dāng)αα=α1,αα1=α1+α2+α3,αα3=α+α2+α3時(shí).

情形16:當(dāng)αα=α1,αα1=α1+α2+α3,αα3=α+α1+α3時(shí).

情形17:當(dāng)αα=α3,αα1=α+α1+α2,αα3=α+α2+α3時(shí).

情形18:當(dāng)αα=α3,αα1=α+α2+α3,αα3=α+α1+α3時(shí).

情形19:當(dāng)αα=α3,αα1=α+α2+α3,αα3=α+α1+α2時(shí).

情形20:當(dāng)αα=α3,αα1=α+α1+α3,αα3=α+α1+α2時(shí).

情形21:當(dāng)αα=α3,αα1=α+α1+α3,αα3=α1+α2+α3時(shí).

類似可得到這些情形都有:α1+α2+α+α3=0,與引理2.1矛盾.

情形22:即αα=α2時(shí),γγ=αα+(αα)q2=α+α2=γ,從而γ=1或0,這與γ生成跡正規(guī)基N相矛盾.

綜上所述M的乘法表為

且CM=3,故M是Fq2在Fq上的最優(yōu)正規(guī)基.這就證明了定理1.4.

3 舉例

本節(jié)考慮q=2和q=8時(shí),Fq4在Fq上滿足條件P的3-型高斯正規(guī)基的對(duì)偶基及跡基的乘法表和復(fù)雜度.

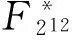
生成F24在F2上的3-型高斯正規(guī)基N,并且

α1=α2=(δ+δ3+δ9)2=

δ2+δ6+δ18=δ2+δ6+δ5,

α2=α12=(δ2+δ6+δ5)2=δ4+δ12+δ10,

α3=α22=(δ4+δ12+δ10)2=

δ8+δ20+δ24=δ8+δ7+δ11.

從而

αα0=α2=α1,

αα1=(δ+δ3+δ9)(δ2+δ6+δ5)=α+α1+α3,

αα2=(δ+δ3+δ9)(δ4+δ10+δ12)=α+α2,

αα3=(δ+δ3+δ9)(δ7+δ8+δ9)=α+α2+α3.

故由α生成的F24在F2上的3-型高斯正規(guī)基N的乘法表為

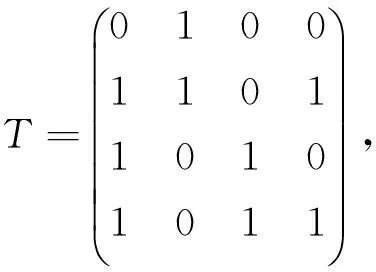
從而N的復(fù)雜度CN=9.進(jìn)而設(shè)N的對(duì)偶基

B={βi=β2i|0≤i≤3},

則由引理1.1以及(1)～(5)式可知

ββ0=1+α22=1+α3=β1,

ββ1=1+α2+α3+α2α3=β1+β2+β3,

ββ2=1+α2+α+α2α=β+β1+β2+β3,

ββ3=1+α2+α1+α2α1=β3.

即B的乘法表為

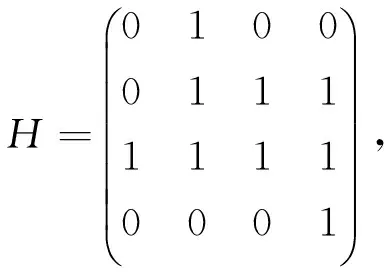
從而B的復(fù)雜度CB=9.又設(shè)N的跡正規(guī)基M={γ,γ2},則由引理2.3知

γ=Tr(α)=α+α22=α+α2,

γ2=Tr(α2)=α2+α23=α1+α3.

故

γγ=αα+(αα)22=α1+α3=γ2,

γγ2=αα1+αα3+(αα1)2+(αα1)22=

α+α2+α1+α3=γ+γ2.

于是

且CM=3.

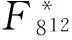
生成F84在F8上的3-型高斯正規(guī)基N,并且

α1=α8=(δ+δ3+δ9)8=

δ8+δ24+δ72=δ8+δ11+δ7,

α2=α18=(δ8+δ11+δ7)8=

δ64+δ88+δ56=δ12+δ10+δ4,

α3=α28=(δ12+δ10+δ4)8=

δ96+δ80+δ32=δ5+δ2+δ6.

從而

αα0=(δ+δ3+δ9)2=δ2+δ6+δ5=α3,

αα1=(δ+δ3+δ9)(δ7+δ8+δ11)=α+α1+α2,

αα2=(δ+δ3+δ9)(δ4+δ10+δ12)=α+α2,

αα3=(δ+δ3+δ9)(δ5+δ2+δ6)=α+α1+α3.

故由α生成的F84在F8上的3-型高斯正規(guī)基N的乘法表為

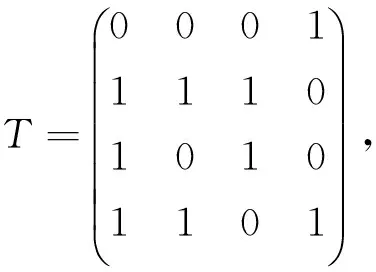
且N的復(fù)雜度CN=9.進(jìn)而設(shè)N的對(duì)偶基

B={βi=β8i|0≤i≤3},

則由引理1.1以及(1)～(5)式可知:

ββ0=1+α22=1+α1=β3,

ββ1=1+α2+α3+α2α3=β2,

ββ2=1+α2+α+α2α=β+β1+β2+β3,

ββ3=1+α2+α1+α2α1=β1.

從而B的乘法表為

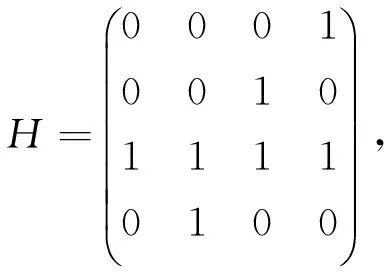
且B的復(fù)雜度CB=7.可見此對(duì)偶基B是F84在F8上的最優(yōu)正規(guī)基.又設(shè)N的跡正規(guī)基M={γ,γ8},則由引理2.3知

γ=Tr(α)=α+α82=α+α2,

γ8=Tr(α8)=α8+α83=α1+α3.

故

γγ=αα+(αα)82=α1+α3=γ8,

γγ8=αα1+αα3+(αα1)8+(αα1)82=

α+α2+α1+α3=γ+γ8.

于是

且CM=3.

致謝 四川師范大學(xué)科研重點(diǎn)培育項(xiàng)目 (13ZDL06)對(duì)本文給予了資助,謹(jǐn)致謝意.

[1] Mullin R, Onyszchuk I, Vanstone S, et al. Optimal bases inGF(pm)[J]. Discrete Applied Math,1988/1989,22(2):149-161.

[2] Gao S, Lenstra H Jr. Optimal normal bases[J]. Design,Codes and Cryptography,1992,2:315-323.

[3] Gao S. Normal Bases over Finite Fields[D]. Ontario:Waterloo,1993.

[4] Wassermann A. Konstruktion von normal basen[J]. Bayreuther Mathematische Schriften,1990,31:155-164.

[5] 廖群英,孫琦. 有限域上最優(yōu)正規(guī)基的乘法表[J]. 數(shù)學(xué)學(xué)報(bào),2005,48(5):947-954．

[6] Christopoulou M, Garefalakis T, Panario D, et al. Gauss periods as constructions of low complexity normal bases[J]. Designs,Codes Cryptography,2012,62(1):43-62.

[7] 廖群英,胡曉蘭. 有限域上一類高斯正規(guī)基的復(fù)雜度的準(zhǔn)確計(jì)算公式[J]. 數(shù)學(xué)學(xué)報(bào),2014,57(5):863-874.

[8] Menezes A J, Blake I F, Gao X H, et al. Applications of Finite Fields[M]. New York:Kluwer Academic Publishers,1993.

[9] Liao Q Y. The gaussian normal basis and its trace basis over finite fields[J]. J Numb Theory,2012,132(7):1507-1518.

[10] Beth T. Generalizing the discrete fourier transform[J]. Discrete Math,1985,56:95-100.

[11] Diffie W, Hellman M. New directions in cryptography[J]. IEEE Trans Inform Theory,1976,22:644-654.

[12] Fumy W. orthogonal transform encoding of cyclic codes[C]//Algebraic Algorithms and Error-Correcting Codes. Lecture Notes Comput Sci. Berlin:Spring-Verlag,1986,229:131-134.

[13] Dahab R, Hankerson D. Software multiplication using gaussian normal basis[J]. IEEE Transaction on Computers,2006,55(8):974-984.

[14] 李波,廖群英. 偶特征有限域上一類正規(guī)基及其對(duì)偶基[J]. 數(shù)學(xué)進(jìn)展,2015,44(3):394-404.

[15] 李俊,黃琴,李波,等. 有限域上k-型高斯正規(guī)基及其對(duì)偶基[J]. 四川師范大學(xué)學(xué)報(bào):自然科學(xué)版,2011,34(3):289-295.

[16] Christopoulou M, Garefalakis T, Panario D, et al. The trace of an optimal normal element and low complexity normal bases[J]. Designs,Codes Cryptography,2008,49(1/2/3):199-215.

2010 MSC：12E20

(編輯 陶志寧)

The Trace and Dual Bases of Some Special Gaussian Normal Bases over Finite Fields with Even Characteristic

LI Xuelian, LIAO Qunying
(CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)

Letqbe a power of 2. Recently, the dual basis of some special Gaussian normal base of the finite filedFqnoverFqis determined in literature(Li B, Liao Q Y. Adv Math(China),2015,44(3):394-404.). The present paper continues the study and determines the complexity of the dual and trace basis for the above Gaussian normal bases completely, and it is proved that the trace basis is optimal.

finite field; Gauss normal basis; dual basis; trace normal basis; multiplication table; complexity

2014-08-22

國家自然科學(xué)基金(11401408)和四川省教育廳重點(diǎn)項(xiàng)目基金(14ZA0034)

O156.2; O157.4

A

1001-8395(2015)06-0802-08

10.3969/j.issn.1001-8395.2015.06.003

*通信作者簡(jiǎn)介：廖群英(1974—),女,教授,主要從事編碼與密碼學(xué)理論的研究,E-mail:qunyingliao@sicnu.edu.cn.