復雜結構部件概率疲勞壽命預測方法與模型

謝里陽*,任俊剛,吳寧祥,錢文學

東北大學航空動力裝備振動及控制實驗室,沈陽 110819

復雜結構和零部件的幾何形狀及受力狀態決定了其多部位損傷(MSD)特征,即一個結構部件或一個復雜機械零件上存在多個可能發生失效的關鍵(高應力/低強度)部位。由于結構和零部件載荷及各部位強度的不確定性,復雜結構和零部件上各損傷部位的疲勞壽命都具有明顯的隨機性。因此,復雜結構和零部件的壽命并不等于確定性意義上最薄弱部位的壽命,其失效及概率壽命預測問題是一個系統的失效及可靠性問題。若結構或零部件上任一部位失效都會導致整個結構或零部件失效,則一個結構或一個零部件就是一個串聯系統。在這樣的系統中,若載荷具有不確定性,則各關鍵部位失效會存在統計相關性,需要有適用的模型預測系統壽命及其概率分布。

近年來,多部位損傷問題得到了極大關注,相關研究包括多裂紋結構的剩余強度問題[1-2]、壽命問題[3]、結構完整性問題[4]等。有許多文獻研究了多部位損傷結構的疲勞壽命預測理論與方法[5-12],但多數研究都是在確定性框架下進行的,或只涉及簡單的概率計算。

關于疲勞壽命的概率分布問題,傳統上多根據P-S-N(應力-概率壽命)曲線預測簡單零件(只含有一個可能失效的部位)在確定性的循環載荷作用下對應于一定可靠度的疲勞壽命,或借助應力-強度干涉模型反映載荷不確定性對疲勞失效概率的影響[13-14]。應用應力-強度干涉模型的前提是獲得對應于某一壽命的疲勞強度概率分布[15],這樣的方法應用難度很大,且適用范圍有限。

變幅載荷歷程下的疲勞失效概率問題更加復雜,相關研究多局限于具體零件或結構[16],且很少涉及多部位損傷問題。Petryna等[17]研究了鋼筋混凝土結構的概率疲勞損傷建模問題,Karadeniz[18]介紹了一種海洋工程結構譜載荷疲勞壽命不確定性分析程序。Kliman[19]介紹了一種基于能量準則估算隨機載荷作用下零件可靠壽命的方法,應用S-N曲線和循環應力-應變曲線、載荷歷程的標準差和概率密度分布、以及由雨流計數法得到的載荷循環譜塊。其失效準則是從能量的觀點進行考慮,累積損傷臨界值為載荷幅值的函數。文獻[20]提出了一個系統可靠性分析的一般方法。本文基于系統失效概率分析及具體損傷部位的概率累積損傷計算,建立多部位損傷結構和零部件概率疲勞壽命預測模型。

1 疲勞失效概率表達方法

指定循環應力水平下的疲勞壽命是一個隨機變量,通常可以用Weibull分布或對數正態分布描述。多級譜載或變幅應力歷程下的疲勞壽命分布可能表現出更為復雜的形式。為了預測零部件在變幅載荷歷程下的概率壽命,首先需要研究變幅應力歷程下的疲勞損傷的概率特性,以及概率疲勞損傷累積方法。為了便于處理變幅應力歷程下的概率疲勞損傷累積問題,本文首先研究變幅載荷歷程下疲勞損傷及其臨界值概率分布的表達式,以及與隨機臨界損傷對應的損傷累積計算方法。

傳統損傷累積模型只涉及確定性量,即確定性的壽命和確定性的應力循環次數。在壽命N為隨機變量的情形,損傷n/N也為隨機變量,n為應力循環次數。若沿用傳統的累積損傷臨界值概念,認為損傷臨界值為1,即損傷臨界值為確定性量,失效判據可表達為

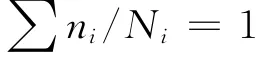
式中:ni為第i應力水平下的應力循環次數；Ni為相應的壽命隨機變量。

相應地,失效概率為

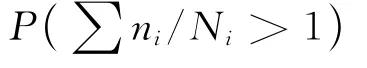
若要應用此式預測疲勞失效概率,需要計算n/N大于1的概率,因而需要確定n/N的概率密度函數。這樣做的困難是,難以由壽命N的概率密度函數推導出損傷n/N的概率密度函數。為了避免這樣的困難,本文首先探討變幅應力作用下疲勞失效概率計算的可能方法。為此,需要分析疲勞損傷累積計算中涉及到的有關變量,尤其是有關確定性量與隨機變量之間的聯系。

在指定循環應力水平si下,壽命為隨機變量,其中值和標準差分別為ˉNi和σi,概率密度函數為fi(N)。當應力循環次數為ni時,失效概率為

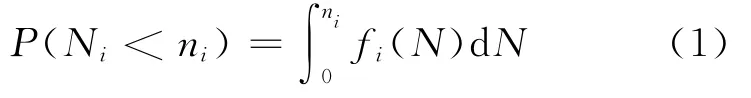
為了便于進行不同應力水平下應力循環次數的損傷等效轉換及進行概率損傷累積,可以進行確定性應力循環次數與壽命隨機變量之間的概率等效變換。具體作法是,為了便于進行失效概率計算,把原本是隨機變量的壽命Ni轉換為確定性量,數值為其中值ˉNi；相應地,把應力循環次數轉換作為以實際循環次數ni為中值的隨機變量,記為nri。對于壽命概率密度函數可用三參數函數(例如三參數 Weibull分布)表達的一般情形,把概率密度函數為fN,i(N)=fN,i(βN,ηN,γN)的壽命隨機變量轉換為以其中值為具體數值的確定性量,把原本確定性的應力循環次數轉換為以其實際循環數為中值,概率密度函數為fn,i(n)=fn,i(βn,ηn,γn)的隨機變量,且有P(nri＞ˉNi)=P(Ni＜ni)成立,即

為了實現這樣的轉換,需要首先以壽命中值為基準,構造壽命概率密度函數的鏡像函數,再將此鏡像函數向左平移一段距離-ni,即可得到對應載荷循環數的概率密度函數。圖1展示了轉換前后的情況。

顯然,既然可以實現這樣的轉換,也就可以以壽命中值為基礎、以對應的等效應力循環次數隨機變量為根據計算概率損傷,把損傷臨界值取為確定性量(取值為1)；或以壽命中值為基礎、以實際的應力循環次數(確定性量)為根據計算“中值”損傷,把損傷臨界值解釋為隨機變量N/。這樣,就可以把累積損傷隨機變量與確定性的累積損傷臨界值1之間的關系轉換為確定性的“中值”累積損傷與累積損傷臨界值隨機變量之間的關系。

在隨機變量(例如對數壽命、對數應力循環數)服從正態分布的情形,為了保證失效概率計算的等效性,應使隨機化后的應力循環數的對數的標準差等于該應力水平下壽命對數的標準差σi,即ln nri的中值(均值)和標準差分別為ln ni和σi。

在這種變換的基礎上,對損傷臨界值可作如下處理。由于壽命Ni為隨機變量,應力循環ni次時損傷為隨機變量ni/Ni,損傷臨界值為ˉNi/ˉNi=1。進行應力循環次數隨機化轉換之后,相應的損傷隨機變量為nri/ˉNi,損傷臨界值同樣為ˉNi/ˉNi=1。由此可見,疲勞損傷隨機變量既可以根據實際應力循環次數以壽命隨機變量為基準計算,也可以根據等效的應力作用次數隨機變量以壽命中值為基準計算。

從損傷臨界值的角度,在某一指定幅值的循環應力作用下的失效概率可表達為

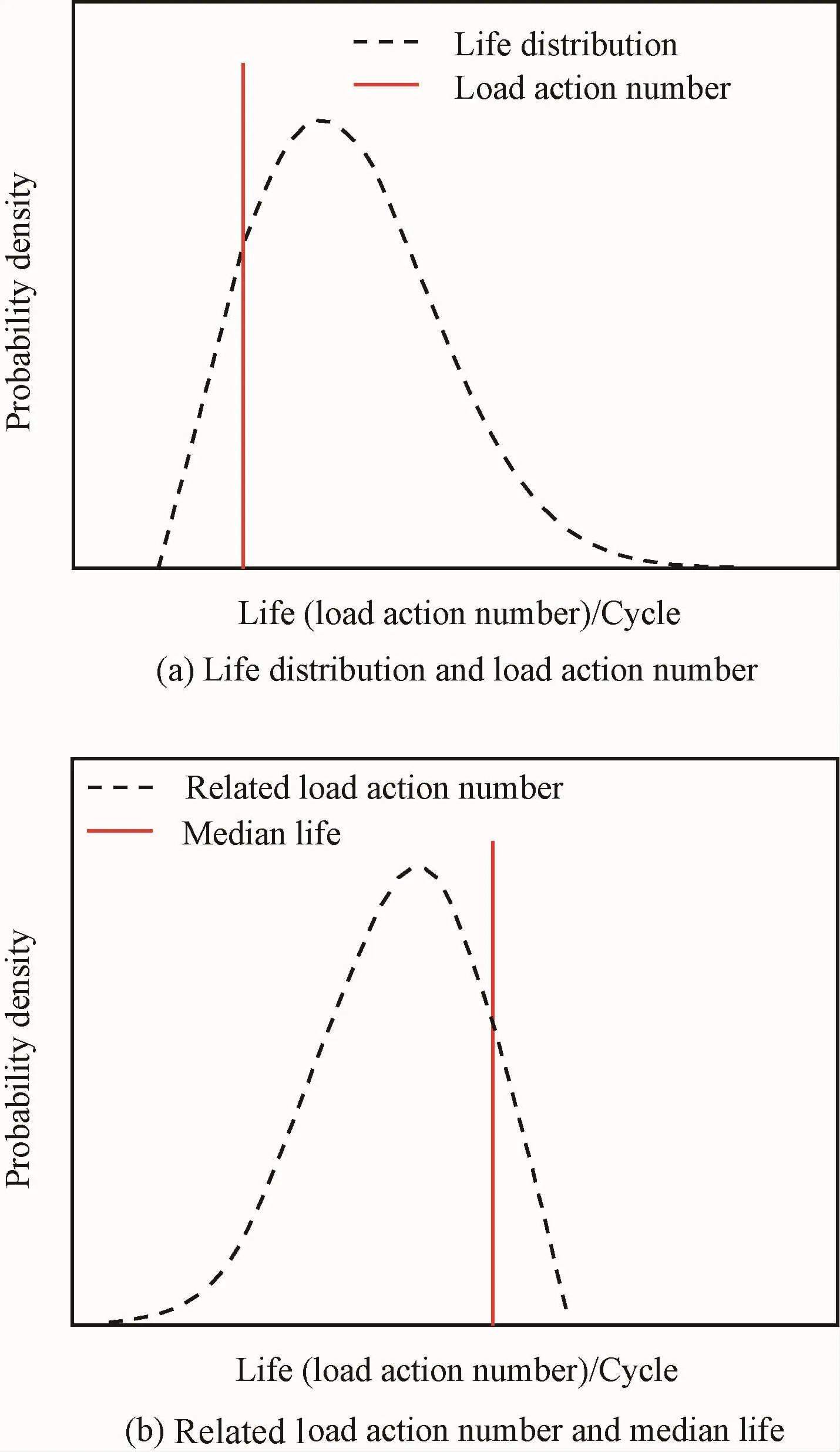
圖1 壽命分布與對應應力循環次數分布變換原理Fig.1 Transform principle of life distribution and equivalent load action number distribution

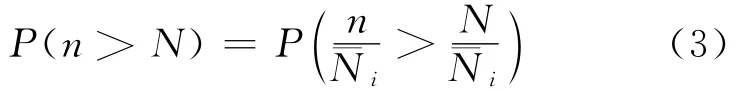
由于n/ˉNi定義為中值損傷,根據式(3),累積損傷的臨界值為隨機變量。在傳統的、確定性意義上的線性累積損傷法則中,損傷臨界值(確定性量)與應力水平無關,因而才可以簡單地進行累積損傷計算、簡單地判定失效何時發生。要建立概率累積損傷法則,也需要清楚概率意義上的損傷臨界值隨機變量與應力水平之間的關系。只有在損傷臨界值的概率分布與應力水平無關的前提下,才能建立像傳統累積損傷法則那樣形式簡單的公式。

定性地講,在壽命概率分布方面,一般規律是低應力、長壽命對應于較大的壽命分散性。對于損傷臨界值的概率分布來說,分散性較大的壽命隨機變量除以較大的壽命均值,使得損傷臨界值的分散性不會像壽命分散性那樣直接與應力水平有關。下面將證明,若不同應力水平下的疲勞壽命Weibull分布的形狀參數相同(這是一種很常見的合理假設),則不同應力水平下的損傷臨界值的分布相同,即與應力水平無關。

若在任一應力水平下壽命均服從Weibull分布,則在基準應力水平其概率密度函數和累積概率分布函數分別為

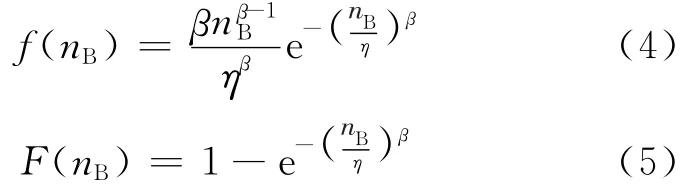
式中:nB為基準應力水平下的壽命；β為形狀參數；η為尺度參數。

損傷臨界值為

式中:下標B表示基準應力水平。

根據確定隨機變量函數概率分布的基本原理,可以得到損傷臨界值的概率密度函數和累積概率分布函數分別為

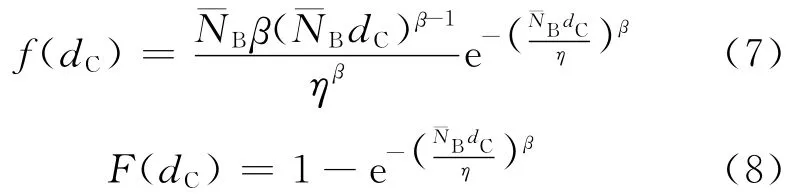
式中:dC為損傷臨界值變量。將Weibull分布中值壽命表達式代入式(8),有

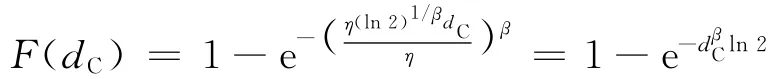
顯然,在β為常數(不隨應力水平變化)的條件下,損傷臨界值的概率分布與應力水平無關。

由于損傷臨界值的概率分布與應力水平無關,可以以任一應力水平(例如S-N 曲線所覆蓋的應力范圍的中間值)下的壽命分布為基準,根據此基準應力水平下的壽命概率分布確定累積損傷臨界值的概率分布。或者根據加權計算確定基準應力水平,即對載荷歷程進行計數,結果劃分為m個應力水平,其中應力si下有ni個載荷循環,則基準應力水平取為

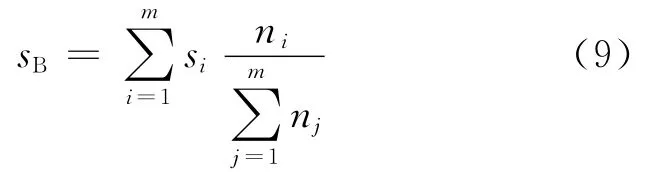
典型壽命分布fN(n)～W(2,200 000)及相應的累積損傷臨界值分布概率密度函數fD(dC)如圖2所示。考察壽命分散性是否對損傷臨界值的概率分布有明顯影響,圖3所示的壽命分布與圖2所示的情形相比有更大的分散性,即其概率密度函數fN(n)～W(1.5,300 000)及相應的累積損傷臨界值分布fD(dC)更分散。可以看出,雖然與圖2所示的情形相比,壽命分布有明顯不同(形狀參數、尺度參數都不明顯相同),但損傷臨界值分布的差異并不是很大。這也定性地支持了損傷臨界值分布對應力水平不敏感的觀點。

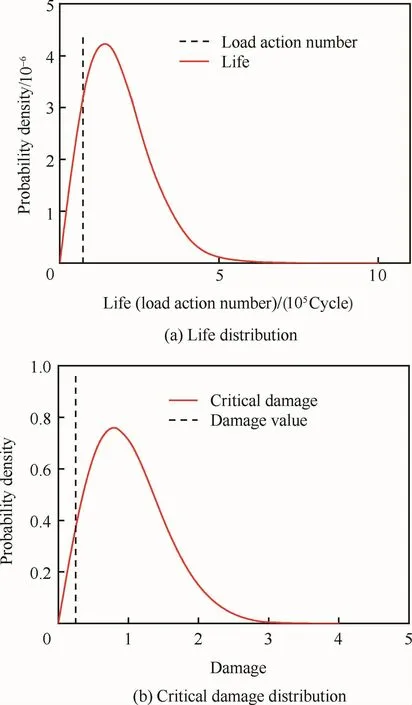
圖2 分散性較小的壽命分布與損傷臨界值分布Fig.2 Life distribution with small dispersion and critical damage distribution

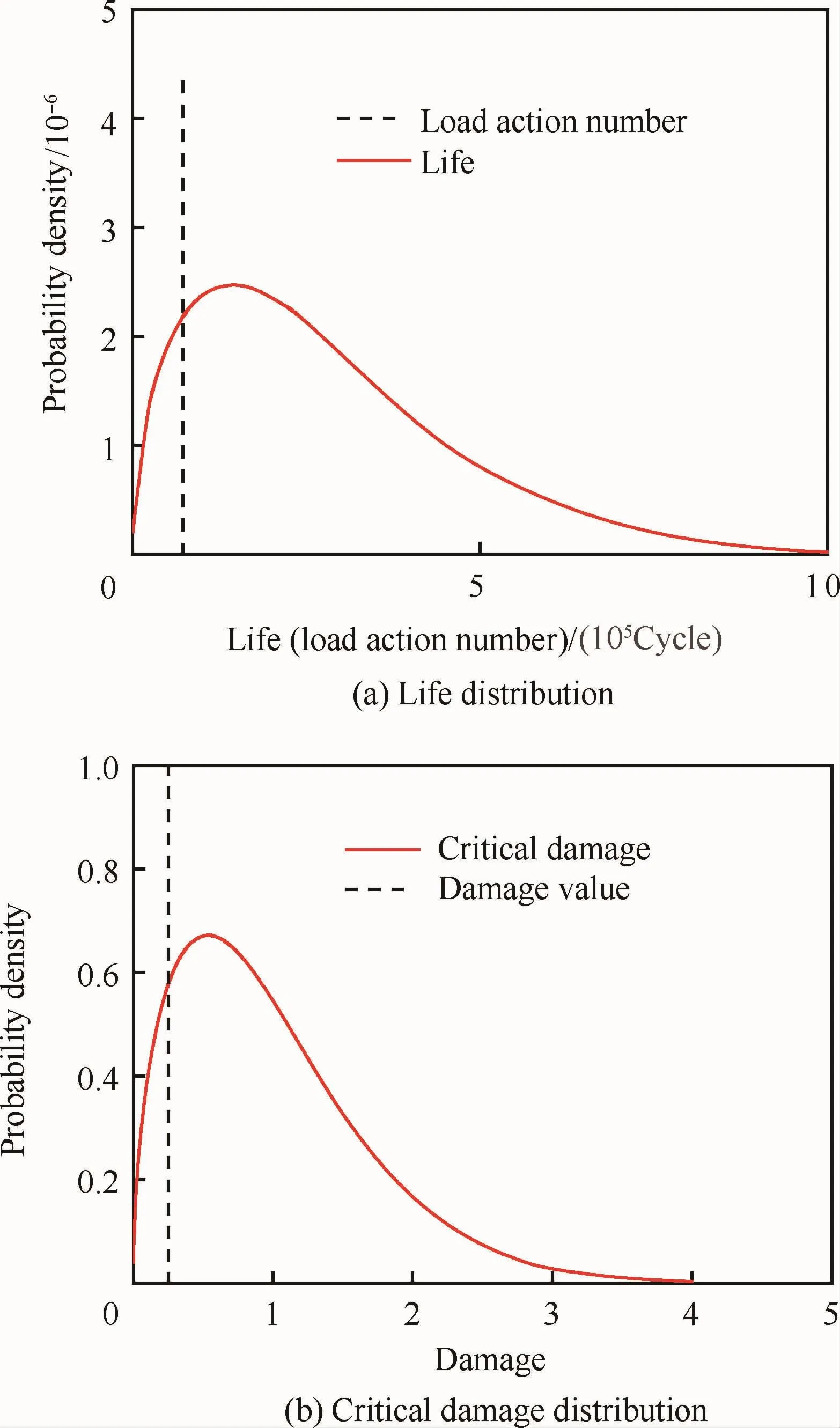
圖3 分散性較大的壽命分布與損傷臨界值分布Fig.3 Life distribution with large dispersion and critical damage distribution

2 概率累積損傷法則

傳統的累積損傷問題只涉及確定性意義上的累積損傷,是在壽命與應力循環數都為確定性量的條件下定義的。由于壽命為隨機變量,對應于一定應力水平、一定循環次數的循環應力產生的損傷也是隨機變量。從材料性能的角度,也可以認為材料所能容許的損傷臨界值為隨機變量,即一批材料試樣中,相對好的試樣能承受更多的應力循環數,而每個應力循環產生的損傷是一定的,只與應力水平有關,與材料性能無關。為了獲得概率壽命或可靠壽命,需要建立概率累積損傷法則。疲勞累積損傷法則的基礎是不同應力水平的循環應力產生的疲勞損傷存在等效性。概率累積損傷法則的一個必須滿足的條件是,不同應力水平下,相同的損傷須對應相同的疲勞失效概率。

根據第1節的闡釋、分析與證明,在進行疲勞損傷累積與概率壽命預測時,可以根據壽命中值計算疲勞損傷及進行損傷累積(稱為中值損傷及中值累積損傷),根據中值累積損傷與累積損傷臨界值的概率分布計算概率壽命——這就是本文要建立的概率累積損傷法則的基本思想。

以不同應力水平下壽命中值為根據折算不同應力水平下的等損傷應力循環次數,即應力sj下的nj個循環產生的疲勞損傷相當于應力si下的ni個循環產生的疲勞損傷,則有

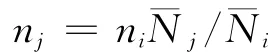
基于損傷臨界值分布與應力水平無關的性質(或假設),可知

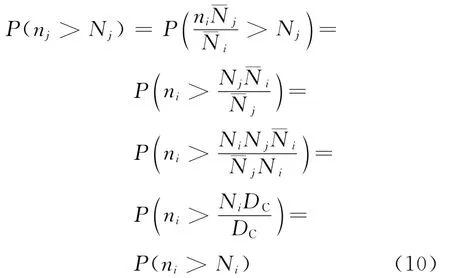
即基于壽命中值折算的不同應力水平下的等效應力循環次數滿足“相同的損傷導致相同的失效概率”的原則(或稱限制條件):

所以,有變幅循環應力作用下的疲勞失效概率計算公式,即概率損傷累積準則:

該法則可表述為,變幅應力作用下的失效概率等于以壽命中值為基準計算的線性累積損傷值小于臨界損傷隨機變量的概率。

3 變幅循環載荷歷程下多損傷部位結構概率疲勞壽命預測

在變幅載荷歷程作用下,多損傷部位結構上,各損傷部位的應力歷程不同,損傷演化歷程也不同。設某結構上含有m個損傷部位,所承受的載荷歷程i(結構可能承受不同的載荷歷程)由應力水平分別為si,1,si,2,…,si,ni的ni個載荷循環構成,損傷部位j(j=1,2,…,m)的應力歷程為,,…

根據線性累積損傷計算公式(Miner法則),以各應力水平下壽命中值為基準計算的損傷部位j的累積損傷(即中值損傷)為

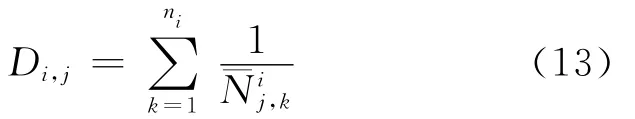
式中:ni為載荷歷程i中所含的載荷循環數；為應力幅為的恒幅循環應力作用下結構上j個損傷部位材料的壽命中值。

在該載荷歷程作用下,損傷部位j的失效的概率為

根據串聯系統概率運算法則,含有m個損傷部位的結構件的失效概率為

考慮到載荷歷程的不確定性,令載荷歷程i出現的概率為pi,可以根據全概率計算原理計算失效概率,即需要把式(17)擴展為

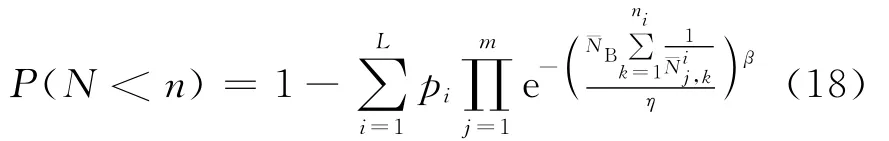
式中:L為載荷歷程樣本數。

4 應用舉例

復雜結構部件上通常包含多個可能失效的關鍵部位。由于各關鍵部位的載荷及材料性能存在隨機性,一個復雜結構部件相當于一個由多個單元構成的串聯系統。因此,對于概率壽命預測而言,多損傷部位結構或機械零部件需要作為一個串聯系統對待。由于同一結構或零部件上各部位的應力是由同源載荷產生的,在載荷及材料強度都具有隨機性的場合,各損傷部位的疲勞損傷或疲勞壽命在統計學意義上既不完全相關,也不相互獨立。因此,多損傷部位結構或零部件的疲勞壽命及可靠性既不能按一個最大損傷部位計算,也不能根據傳統的串聯系統可靠性模型計算。

圖4所示為承受拉伸載荷的帶有5個孔的490 mm×180 mm的板狀零件。顯然,該零件上有10個易損傷部位,即各孔邊應力集中處。由于材料性能分散性的原因,即使在相同的循環應力作用下,各易損部位的損傷演化也會有顯著差異。

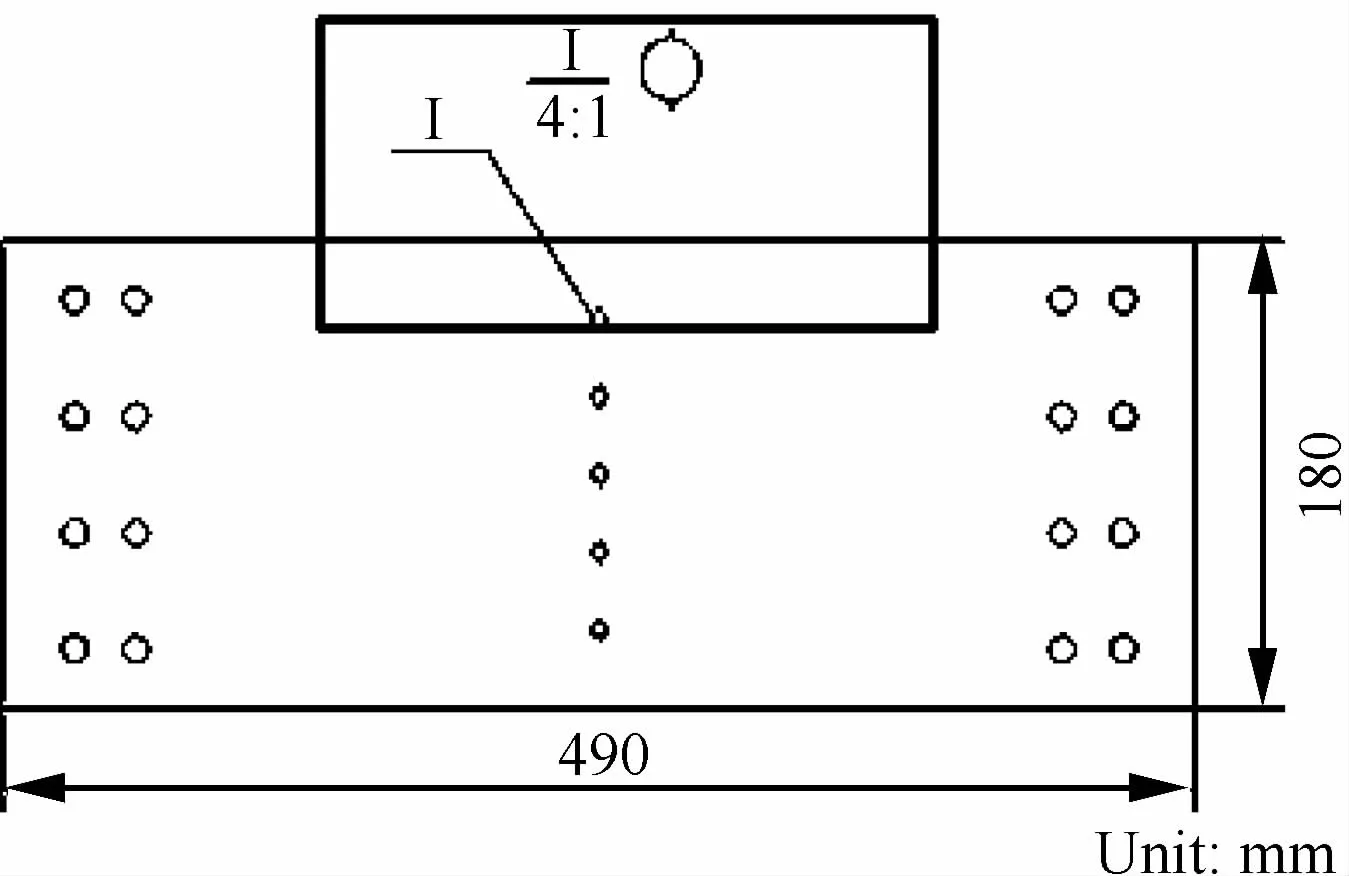
圖4 多部位損傷結構Fig.4 Multi-site damage structure

令各損傷部位的應力歷程相同。應力歷程用應力幅值序列表示,該序列由400～500之間均勻分布隨機數構成,圖5所示為該循環應力歷程的前20個應力循環。

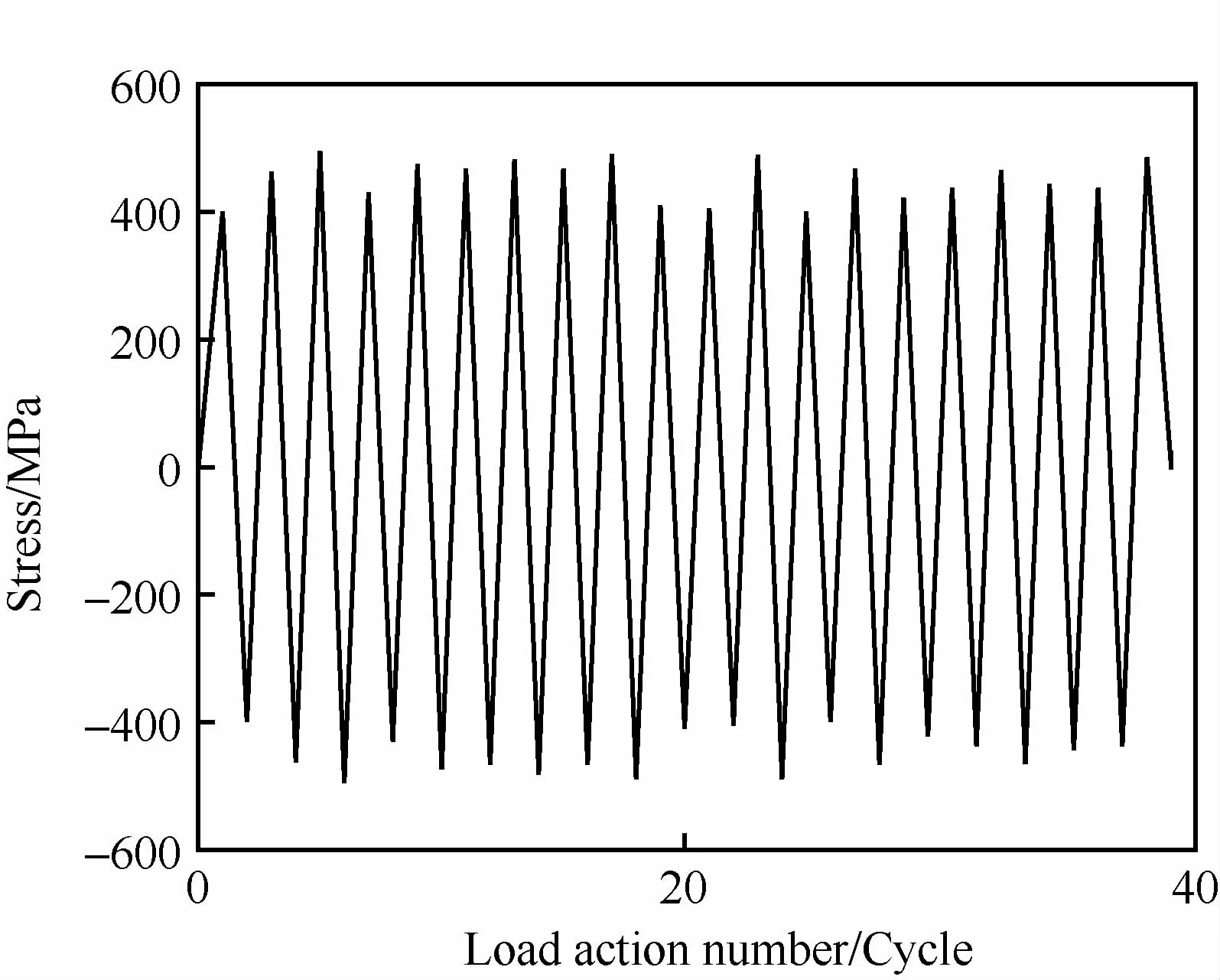
圖5 預測壽命用的應力歷程(部分)Fig.5 Load history used to fatigue life prediction(part)

令材料的應力-概率壽命性能數據如下:

材料的中值S-N曲線方程為

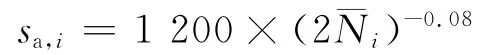
指定應力水平下的壽命服從Weibull分布,且分散性與應力水平無關。在基準應力水平(450 MPa)下,壽命概率密度函數為

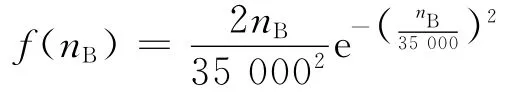
對應于基準應力水平的循環應力作用下疲勞壽命中值為

根據本文介紹的累積損傷計算方法,容易得到累積損傷與載荷循環之間的關系,如圖6所示。

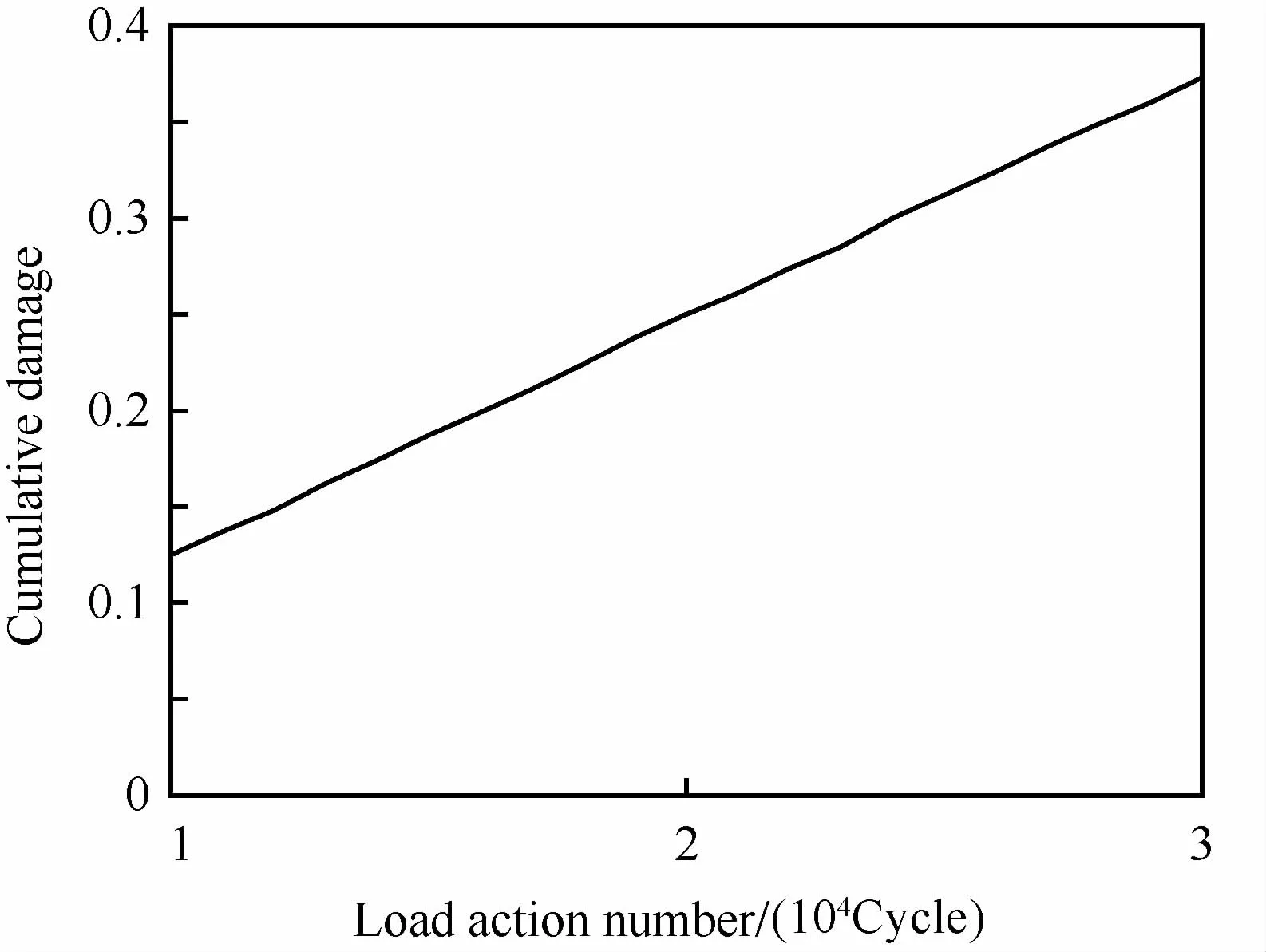
圖6 累積損傷與載荷循環數之間的關系Fig.6 Relationship between cumulative damage and load action number

繼而,根據本文推導出的一個損傷部位的失效概率計算式(15)及多部位損傷零部件的失效概率計算式(17),可以得到失效概率與載荷循環次數之間的關系,如圖7所示。

由計算結果可知,在給定失效概率時,含有多個損傷部位的復雜零部件的壽命會比只有一個損傷部位時的壽命低很多,這是由壽命的不確定性效應導致的。顯然,壽命的隨機性越大,多損傷部位復雜零部件的壽命與只有一個損傷部位時的壽命差別也越大。

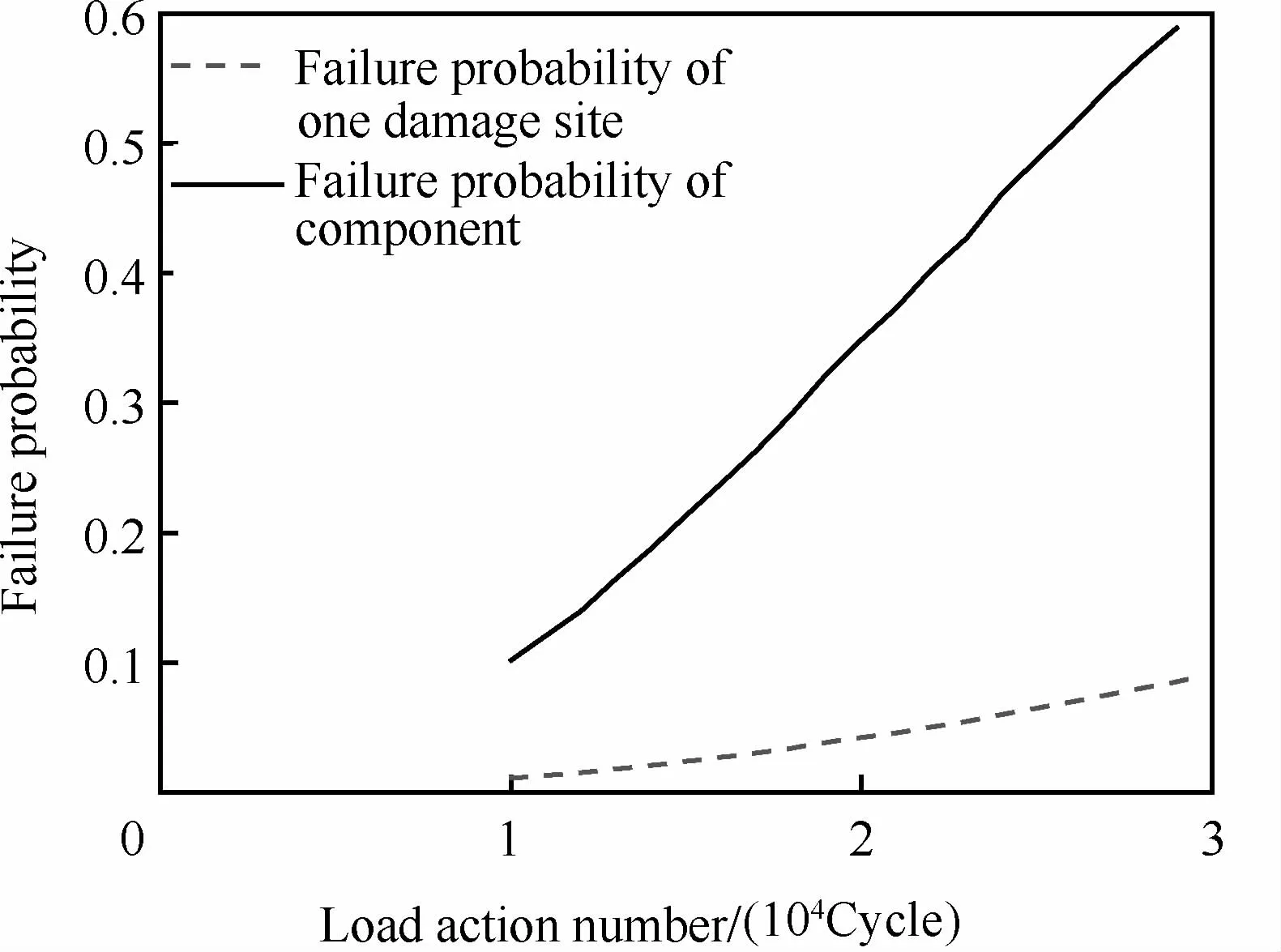
圖7 失效概率與載荷循環次數之間的關系Fig.7 Relationship between failure probability and load action number

5 結 論

提出了一種基于壽命中值計算疲勞累積損傷的概率損傷法則(中值累積損傷法則)以及確定損傷臨界值概率分布的方法。以中值累積損傷法則為基礎,應用多層統計分析及全概率原理,提出了多部位損傷結構和復雜零部件的概率壽命預測方法及模型。中值累積損傷法則體現了疲勞損傷等效與疲勞失效概率等效的一致性。提出的概率壽命預測方法應用方便,需要的材料性能數據只有中值S-N曲線和某一應力水平下的壽命分布,且能反映載荷歷程的隨機性對壽命及可靠性的影響。算例顯示,多損傷結構零部件的概率疲勞壽命與只有一個損傷部位時的概率疲勞壽命有明顯差別。如果只根據零部件上多個較高應力部位中的一個最高應力部位預測其疲勞壽命,會導致偏于危險的結果。

[1] Silva L F M,Goncalves J P M,Oliveira F M F,et al.Multiple-site damage in riveted lat-joints:Experimental simulation and finite element prediction[J].International Journal of Fatigue,2000,22(4):319-338.

[2] Mkaddem A,Mansori M E.An equivalent ellipse method to analyze the fatigue behavior following‘multi-surface initiations’[J].International Journal of Mechanical Sciences,2010,52(9):1125-1135.

[3] Jones R,Molent L,Pitt S.Study of multi-site damage of fuselage lap joints[J].Theoretical and Applied Fracture Mechanics,1999,32(2):81-100.

[4] Park J H,Singh R,Pyo C R,et al.Integrity of aircraft structural elements with multi-site fatigue damage[J].Engineering Fracture Mechanics,1995,51(3):361-380.

[5] Lee H,Kim N.Fatigue life prediction of multi-spot-welded panel structures using an equivalent stress intensity factor[J].International Journal of Fatigue,2004,26(4):403-412.

[6] Salvini P,Vivio F,Vullo V.Fatigue life evaluation for multi-spot welded structures[J].International Journal of Fatigue,2009,31(1):122-129.

[7] Wang X,Modarres M,Hoffman P.Analysis of crack interactions at adjacent holes and onset of multi-site fatigue damage in aging airframes[J].International Journal of Fracture,2009,156(2):155-163.

[8] Park J H,Atluri S N.Fatigue growth of multiple-cracks near a row of fastener-holes in a fuselage lap-joint[J].Computational Mechanics,1993,13(3):189-203.

[9] O’Donoghue P E,Atluri S N,Pipkins D S.Computational strategies for fatigue crack growth in three dimensions with application to aircraft components[J].Engineering Fracture Mechanics,1995,52(1):51-64.

[10] Markiewicz I.Analysis of hole arrangement in tensile plate by means of the SADSF method and fatigue life predictions[J].Maintenance and Reliability,2009,43(3):24-31.

[11] Zhao J M,Chan A H C,Roberts C,et al.Reliability evaluation and optimization of imperfect inspections for a component with multi-defects[J].Reliability Engineering and System Safety,2007,92(1):65-73.

[12] Proppe C.Probabilistic analysis of multi-site damage in aircraft fuselages[J].Computational Mechanics,2003,30(4):323-329.

[13] Lambert S,Pagnacco E,Khalij L.A probabilistic model for the fatigue reliability of structures under random loadings with phase shift effects[J].International Journal of Fatigue,2010,32(2):463-474.

[14] Ni K,Mahadevan S.Strain-based probabilistic fatigue life prediction of spot-welded joints[J].International Journal of Fatigue,2004,26(7):763-772.

[15] Murty A S R,Gupta U C,Krishna A R.A new approach to fatigue strength distribution for fatigue reliability evaluation[J].International Journal of Fatigue,1995,17(2):85-89.

[16] Zhang D,Hong J,Ma Y,et al.A probability method for prediction on high cycle fatigue of blades caused by aerodynamic loads[J].Advances in Engineering Software,2011,42(12):1059-1073.

[17] Petryna Y S,Pfanner D,Stangenberg F,et al.Reliability of reinforced concrete structures under fatigue[J].Reliability Engineering and System Safety,2002,77(3):253-261.

[18] Karadeniz H.Uncertainty modeling in the fatigue reliability calculation of offshore structures[J].Reliability Engineering and System Safety,2002,74(3):323-335.

[19] Kliman V.Fatigue life estimation under random loading using the energy criterion[J].International Journal of Fatigue,1985,7(1):39-44.

[20] Xie L Y,Zhou J Y,Wang Y Y,et al.Load-strength order statistics interference models for system reliability evaluation[J].International Journal of Performability Engineering,2005,1(1):23-36.