基于旋量理論的Stanford機器人的逆運動學分析
王曉磊,李曉丹
(遼寧工業大學機械工程與自動化學院,遼寧錦州 121001)
0 前言
機器人逆運動學也即是求機器人運動學的反解,是指在給定機器人末端執行器的位置和姿態后,求解與該位置和姿態相關各關節的輸出變量,它在機器人的運動學、動力學及控制中起著非常重要的作用。它的求解速度和精度直接影響著該機器人運動的快速性和準確性。傳統的串聯機器人的運動學方程多采用D-H變換矩陣,D-H變換矩陣法相對成熟,但會產生大量的矩陣相乘計算,計算復雜。運用旋量理論可以把復雜的空間機構問題變得十分簡單,它已經廣泛地應用到機器人領域中[1-5]。
1969年Victor Scheinman設計了Stanford機器人,目前已被廣泛地應用于教學和工業生產中。董明曉[6]和趙軻[7]等均在D-H齊次變換矩陣的基礎上推導出逆運動問題算法。本文作者對Stanford機器人的逆運動分析采用旋量理論的方法,通過指數積公式建立機器人正運動學數學模型,根據該機器人的結構特點,應用Paden-Kahan子問題求解Stanford機器人的運動學逆解。
1 旋量基礎
任何剛體從一個位形到另一位形的運動都可以通過繞空間某直線旋轉θ角加上沿該直線的平移距離d合成,此復合運動稱為旋量運動。而其無窮小量稱為運動旋量,文獻[8]詳細推導了用運動旋量的矩陣來表示剛體的運動,如公式(1)所示。
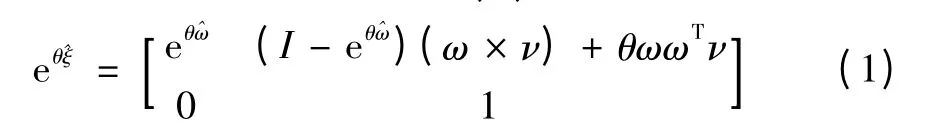
式中:^ξ表示剛體的瞬時速度在SE(3)中的元素,ξ表示關于該軸線的單位旋量坐標。

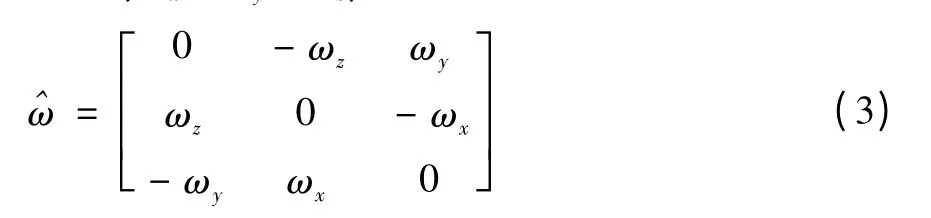
對于多自由度的串聯機器人,只需要2個坐標系,即基座坐標系{S}和末端執行器固定的工具坐標系{T}。定義機器人的初始位形為θ=0時位形,用gST(0)來表示。從初始位形時{T}與{S}之間的變換可表示為
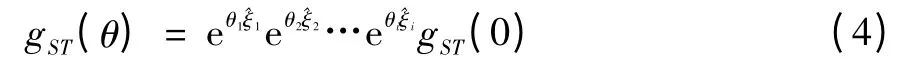
2 Paden-Kahan子問題簡介
從式(1)可以看出機器人的各關節變量具有強耦合的特點,若求其運動學逆解必有一定的困難,因此通常利用Paden-Kahan子問題來消除耦合變量,簡化求解的工作量。Paden-Kahan子問題主要有2個:
(1)點a沿ξ軸旋轉到點b求解滿足條件的θ。
(2)一點繞兩個有序相關軸ξ1和ξ2的旋轉,a、b是空間兩點,其求解過程可轉化為兩個子問題分別求解θ1θ2。θ2為點a繞軸ξ2旋轉的角度,接著再繞軸ξ1旋轉的角度為θ1,最后點a與點b重合。
上述的2個子問題具體推導過程及求解結果見文獻[8]。
3 Stanford機器人的逆解分析
Stanford機器人是一種結構比較特殊的工業機器人,其中前2個關節軸線交于1點,而后三個關節軸線交于一點,結構模型見圖1。利用Paden-Kahan子問題求解Stanford機器人的逆解可消除耦合變量,可簡化計算量。具體的求解過程如下:
(1)初始位形的選擇及指數積正解數學模型建立
取圖示位置為參考圖形;位置即θ=0時并建立工具坐標系和慣性坐標系。θ為0時慣性坐標系與工具坐標系的變換為
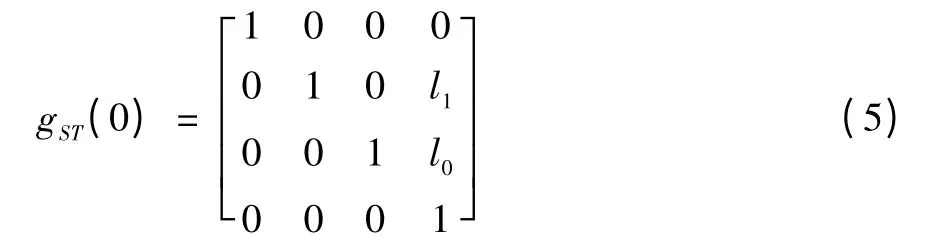
根據式(4),可得
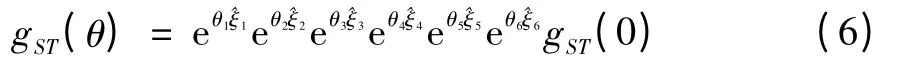
則:
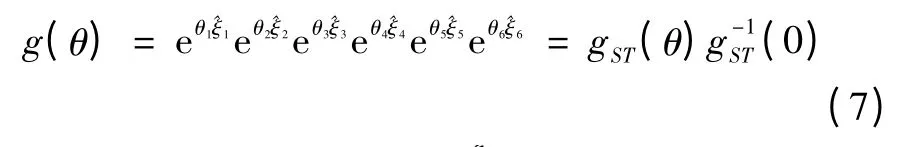
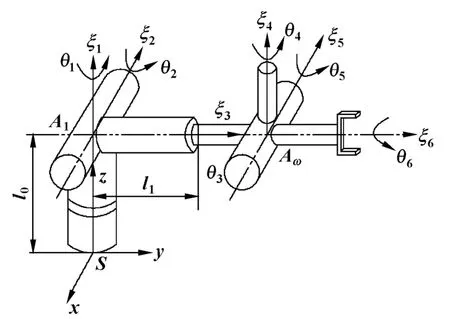
圖1 Stanford機器人模型圖
(2)求前3個關節變量θ1、θ2、θ3
由于4,5,6軸交于一點Aω,所以位于3軸交點Aω無論后3軸如何旋轉其位置保持不變即

將式(7)兩邊同乘Aω,可得:
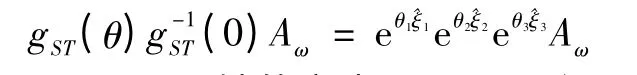
再取1,2軸的交點A1,同理得,
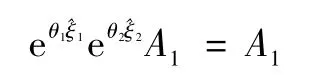
式(8)兩邊減去A1得:由距離不變原則:
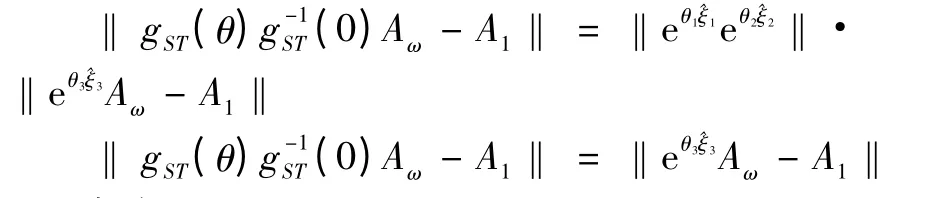
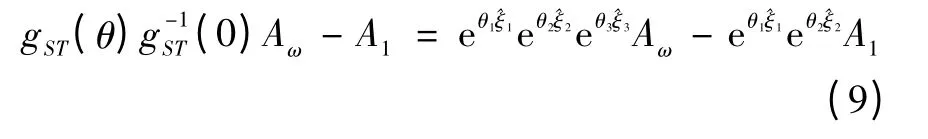
解得θ3。
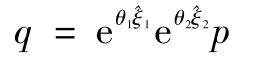
根據Paden-Kahan子問題2可解得θ1、θ2。
(3)求后3個關節變量θ4、θ5、θ6
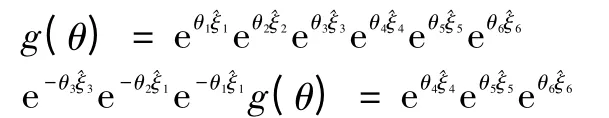
取在6軸,但不在4,5軸一點B,可得
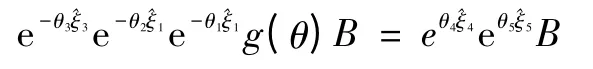
同理根據Paden-Kahan子問題2可解得θ4、θ5。
由已解得θ1~θ5,根據式(7)即可求出θ6。
4 實例驗證
Stanford機器人的主要參數
l0=750,l2=300
首先給定角度依據機器人正解方程,求出機器人的末端位姿矩陣,應用上述逆解的求解過程,求出相應的角度。設給定角度
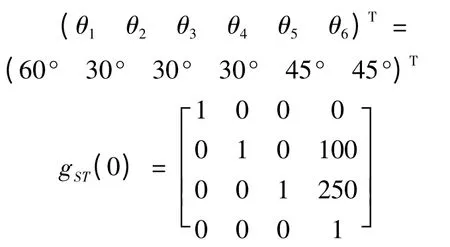
根據正解方程(7)求得末端位姿矩陣:

采用文中給出的逆解方法得出
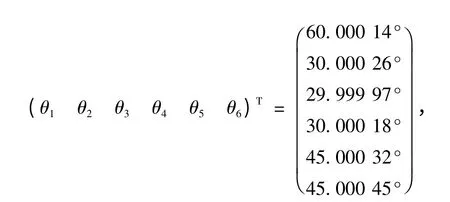
再代入運動學正解位姿矩陣(7),求得末端姿態得:

比較一下結果可以看出該算法精度較高,接近真實值。
5 結束語
根據Stanford機器人結構特點,采用Paden-Kahan子問題將Stanford機器人運動學逆解問題劃分成若干子問題,使其逆解求解更快、更直接,提高了計算效率,有利于計算機對機器人的實時控制;同時通過具體實例驗證可知該算法正確,精度較高,為求解Stanford機器人運動學逆解提供了一新途徑。
[1]趙杰,劉玉斌,蔡鶴皋.一種運動旋量逆解子問題的求解及其應用[J].機器人,2005,27(3):163-167.
[2]王小榮,楊晉,劉瀟瀟,等.仿人機器人基于旋量理論的運動學分析方法[J].蘭州交通大學學報,2009,29(1):72-76.
[3]李君.基于旋量理論的Stanford臂的運動學分析[J].天津科技大學學報,2010,25(4):72-75.
[4]王科.基于旋量和李群李代數的SCARA工業機器人研究[D].杭州:浙江大學,2010.
[5]黃勇剛,杜力,黃茂林.基于旋量理論的機器人誤差建模方法[J].哈爾濱工業大學學報,2010,42(3):484-489.
[6]董明曉,張明勤,趙志超.Stanford機器人逆運動問題求解新方法[J].機床與液壓,2001,12(2):52-53.
[7]趙軻.Stanford機器人逆解關節變量新方法[J].茂名學院學報,2005,15(1):35-36.
[8]理查德摩雷,李澤湘,夏思卡薩思特里,等.機器人操作的數學導論[M].北京:機械工業出版社,1998.
- 機床與液壓的其它文章
- Manufacturing of self-lubricating diamond tools with Ni-Cr alloy adding with Ni/C
- Vibration response analysis of a lathe spindle by using the ANSYS finite element method
- Car following model with consideration of the vehicle’s mechanical inertia effect and its stability analysis
- Software design for spur gear tooth thickness based on MATLAB/GUI
- Dynamic study on ultrasonic horn
- Analysis and research of OPC technology in coal mine monitoring data transmission system

