五自由度并聯機器人機構運動性能優化研究

李瑞霞

(長治醫學院生物醫學工程系，山西長治 046000)

0 前言

并聯機構由于其本身具有的諸多優點，如剛度高、承載能力強、動態性能好、速度快和結構簡單等，受到了國際學術界和工程界的廣泛重視［1－2］。陳修龍等［3］對4-UPS-UPU并聯式坐標測量機的靈巧度從7個性能指標進行了研究，齊明［4］對4-UPS/UPU 5自由度并聯機構進行了分析，提出給定工作空間使其操作性能最優的尺度綜合方法，吳文強等［5］對串聯機器人的性能指標進行了優化分析，Tao等［6］對三轉動并聯機構進行了性能指標優化分析，對于對立的性能指標提出加權因子，李明磊等［7］提出了基于差異演化算法對并聯機構進行結構優化。

本文作者以一種可實現5自由度的4-UPS-UPU并聯機器人機構為研究對象，建立其運動學模型及雅克比矩陣，考慮機構在運動空間內的運動學性能，引入全域條件指標和全域梯度指標為優化目標，基于多學科設計優化軟件Modefrontier對機構進行了多目標優化研究。采用柱坐標極限搜索法求解機構工作空間，通過求解其全域條件指標的近似值，得到優化目標的數學模型;采用實驗設計和粒子群優化算法對機構進行了優化求解，求得最優Pareto解，對優化前后的運動性能進行了比較分析，為并聯機構多目標優化設計提供參考依據。

1 4-UPS-UPU并聯機構模型

1.1 并聯機構描述

4-UPS-UPU并聯機構的模型及坐標系的建立如圖1所示，該機構由動平臺、定平臺及連接動平臺和定平臺的4條完全相同的驅動支鏈UPS以及1條驅動支鏈UPU組成。4個完全相同的驅動支鏈由1個虎克鉸，1個移動副和1個球鉸按照U-P-S的順序連接而成。另一驅動支鏈由一個移動副和兩個虎克鉸按照U-P-U的順序連接而成［8］。

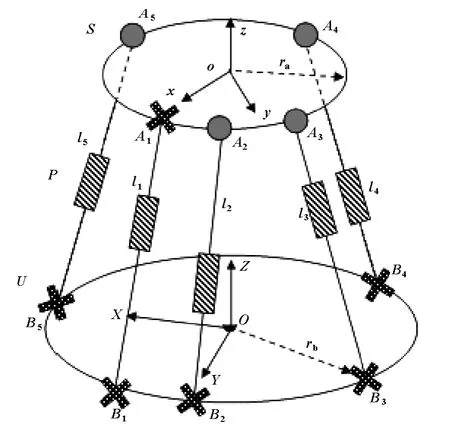
圖1 4-UPS-UPU并聯機構簡圖

以該并聯機構的動靜平臺的幾何中心o、O為原點，分別建立機構的相對坐標系o－xyz和參考坐標系O－XYZ，動平臺外接圓半徑為ra，x軸指向點A1，鉸點Ai在動平臺圓周上均勻分布，z軸垂直于動平臺方向向上，y軸正方向按右手定則給定;靜平臺外接圓的半徑為rb，X軸指向B5，B1與X軸正向夾角為45°，其余4個虎克鉸相距90°均勻分布，Z軸垂直于定平臺方向向上，Y軸由右手螺旋定則給定。

1.2 自由度的計算

根據傳統的自由度求解公式

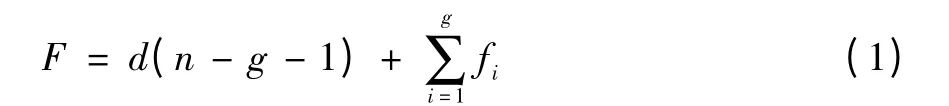
式中:F為機構的自由度，n為構件數，g為運動副數，fi為第i個運動副的自由度數。d為機構的階數，當機構為空間機構時，式中的d=6。球副的自由度為3，虎克鉸的自由度為2，移動副的自由度為1。該機構中，則F=5。即動平臺具有X軸、Y軸、Z軸移動的自由度以及繞X軸、Y軸轉動的自由度。

1.3 機構位置分析

動平臺鉸點Ai在相對坐標系oxyz和參考坐標系OXYZ下的矢量坐標可以表示為(Aix，Aiy，Aiz)T和(AiX，AiY，AiZ)T。

靜平臺鉸點Bi在相對坐標系O－XYZ下的坐標為(BiX，BiY，BiZ)T。

點Ai從坐標系o－xyz轉換到坐標系O－XYZ下表示為

式中:P=[x y z]T表示相對坐標系o－xyz原點在定坐標系下的位置矢量，根據RPY變換理論，可得旋轉矩陣Q為

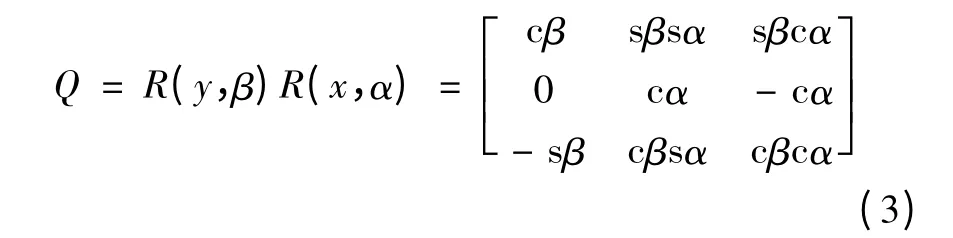
式中:sβ=sinβ，cβ=cosβ，其余類似。

驅動桿的長度矢量表達式為

則驅動桿的長度li為

若已知動平臺的位姿，即可求出各連桿長度，即運動學逆解。

1.4 雅可比矩陣分析

對于并聯機構4-UPS-UPU，雅可比矩陣反映驅動關節速度與動平臺速度之間的映射關系。設動平臺o點的線速度，動平臺的角速度ω=，鉸點Ai的速度可表示為

則第i條支鏈的驅動速度l·

i可表示為

其中si為驅動支鏈的單位向量

把式(6)代入式(7)中，得

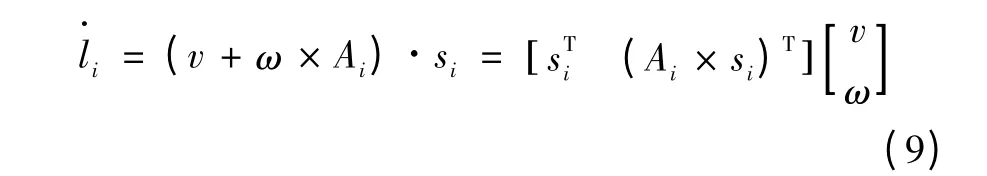
則并聯機構的雅可比矩陣為

2 機構運動性能指標的建立

2.1 全域條件指標

Gosseli［9－10］提出了全域條件指標，能夠評估機構在整個工作空間上的運動性能，公式定義為其中ν為局部條件數，ν=1/κ(J)，κ(J)為雅可比條件數，κ(J)=‖J‖·‖J-1‖，‖·‖為矩陣的譜范數，W為工作空間。

全域條件數越大，說明整個工作空間的靈巧度越佳，因此，應使優化目標GCⅠ處于最大化。

2.2 全域梯度指標

F A LARA-MOLINA［11－12］提出了全域梯度指標，它代表局部條件數的波動情況，定義為

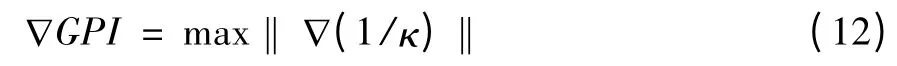
其中局部條件數的梯度可以表示為

GPⅠ近似等于整個工作空間下局部梯度的最大值，若梯度越小，說明整個工作空間的靈巧度波動性越小。于是，希望全域梯度指標取最小。

2.3 工作空間求解

為了求解全域條件指標和全域梯度指標，需要求解該并聯機構的工作空間。本文采用柱坐標極限搜索法對4UPS-UPU并聯機構定位姿(α=0，β=0)下位置工作空間求解。通過搜索空間中動平臺參考點的位置對應的桿長和運動副轉角以及奇異性判斷是否符合限制條件，判斷該位置點是否在工作空間內。搜索工作空間的流程圖見圖2。

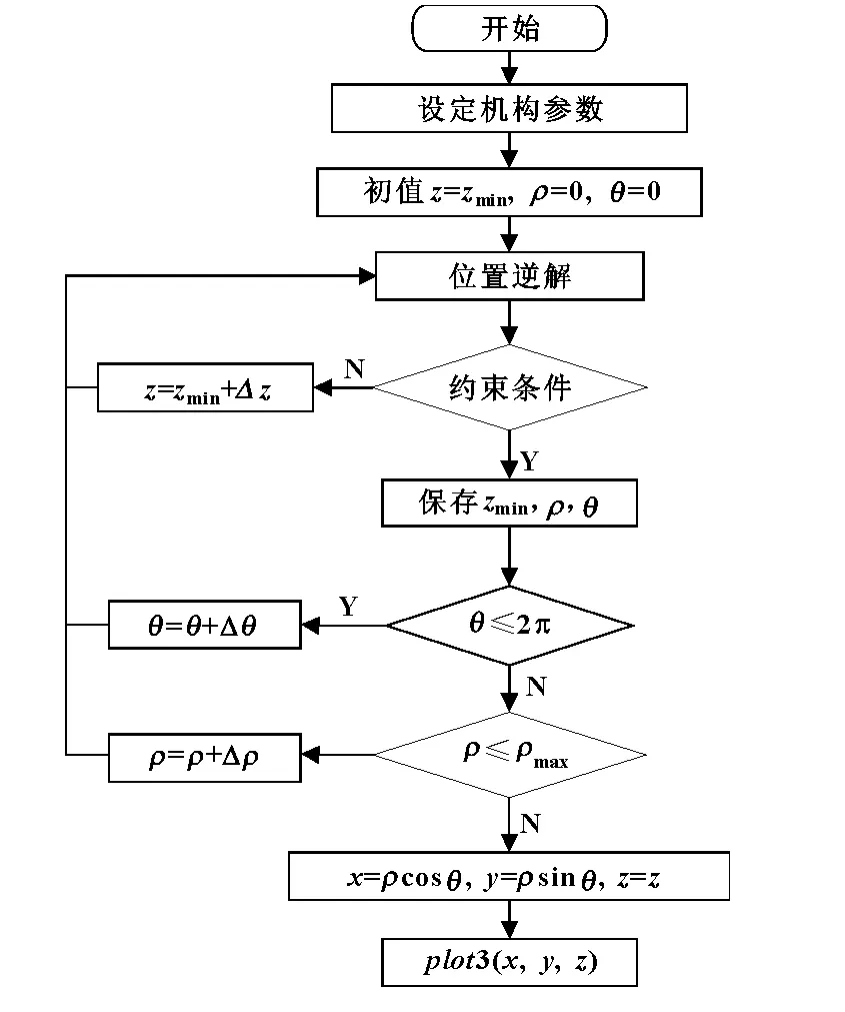
圖2 并聯機構工作空間搜索流程圖

具體的步驟為:

(1)將工作空間用平行于XY平面的的平面簇將Z軸分成n等份，沿Z軸以步長為Δz的子空間從Zmin到Zmax進行搜索;

(2)每一子空間z'內，采用柱坐標確定子空間，動平臺參考點o在參考坐標系下的坐標為(ρcosθ，ρsinθ，z)。極角θ從0到2π以步長為Δθ=2π/100搜索，極徑從ρ=0以步長Δρ=0.01 m搜索至ρmax=0.5 m。

(3)在搜索過程中，判斷動平臺參考點是否滿足約束條件。如果機構滿足約束條件且至少有一個取等號，則該點為工作空間的邊界點，從而得到每個截面上的邊界線，最終由邊界線描繪出工作空間的三維輪廓;

(4)將柱坐標系下的ρ、θ轉化到笛卡爾坐標系下，x=ρcosθ，y=ρsinθ。用坐標(x，y，z)表示，Matlab繪制機構工作空間的三維圖形。

機構參數初始值見表1。

表1 機構參數表

借助MATLAB軟件編寫工作空間程序，可求得機構的三維工作空間，如圖3所示。

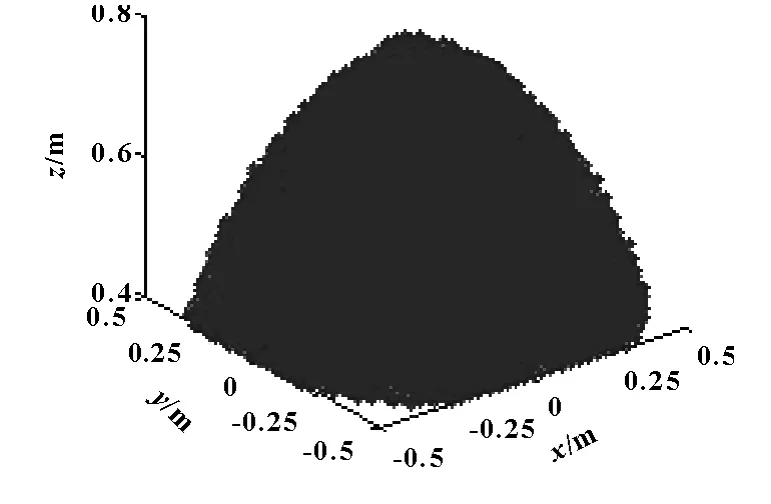
圖3 4-UPS-UPU并聯機構的工作空間

3 優化模型的建立

選擇該并聯機構的結構參數lmin=0.4為固定值，ra、rb、lmax作為設計變量;優化目標為機構的全域條件指標GCⅠ和全域梯度指標GGⅠ，則機構的多目標優化模型為

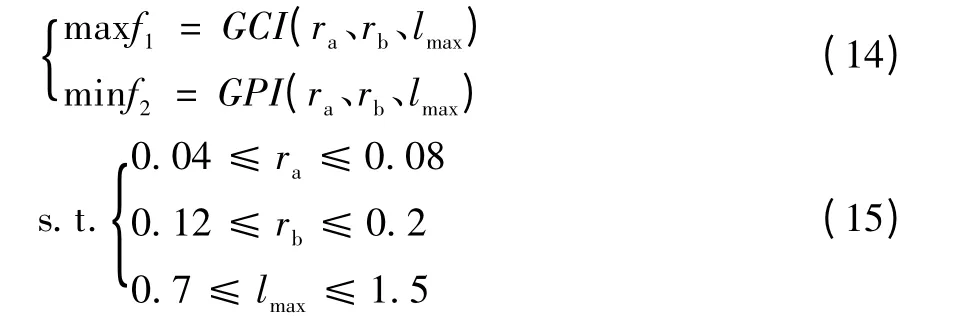
4 優化結果分析

Modefrontier集成MATLAB，采用實驗設計、優化算法來求解GCⅠ的最大值和GPⅠ的最小值。實驗設計采用最優拉丁超立方設計，粒子群優化算法參數配置如下［13］:粒子種群大小為40，粒子個數設為10，慣性權重為0.9，全局增量為0.9，粒子增量為0.9，決定在當前位置與最好位置之間的區域分辨率的最大速度為0.1，運行失敗的罰值為1030，運行失敗的目標值為1030。任務組合流程圖如圖4所示。

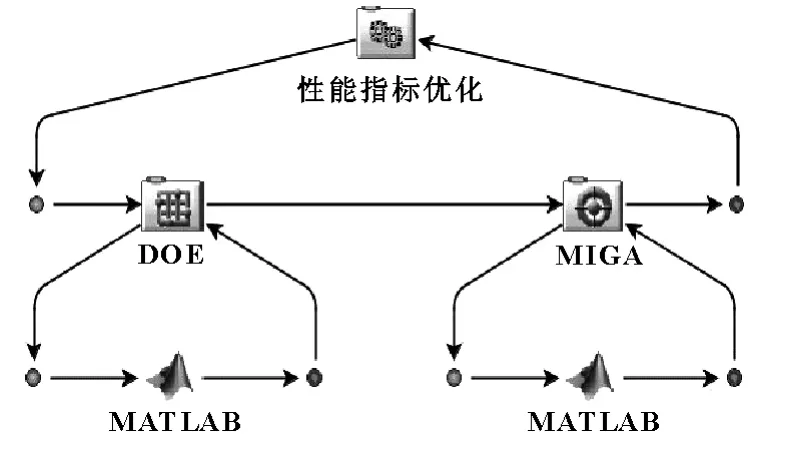
圖4 Modefrontier多目標優化任務流程圖

Modefrontier在進行多目標優化過程中，實驗設計會對優化模型進行計算，并剔除不符合約束條件的值，滿足約束條件的值會進入優化環節，進行多目標優化求解，多次遺傳迭代后可得到全域條件性能指標和全域梯度指標的Pareto解集，如圖5所示。

圖5 全域性能指標的Pareto解集

設計變量對性能指標的影響如圖6、7所示。

圖6 ra、rb對全域條件指標的影響圖

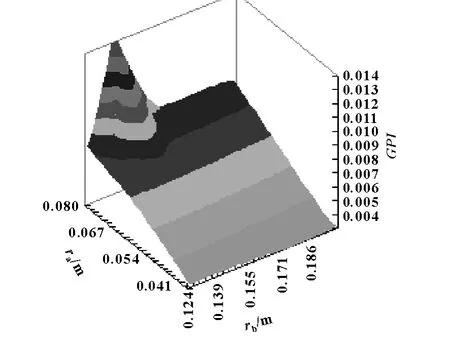
圖7 ra、rb對全域梯度指標的影響圖

從圖5可以看出，全域條件指標和全域梯度指標是近似正相關，這是兩個相互沖突的指標，增大GCⅠ的同時也會增大GPⅠ。從圖6和圖7可以看出，隨著設計變量的增大，性能指數也在增加，因此，需要設計者從Pareto解中選擇符合要求的解。

選擇P點作為可行解，比較優化前后目標函數變化情況，見表2。

表2 設計變量與性能指標優化前后結果比較

優化前GCⅠ=0.093，GPⅠ=0.9×10－2;優化后GCⅠ=0.122，GGⅠ=0.97×10－2，全域條件指標增大了30%，而全域梯度指標僅僅增大7%。

多目標優化不同于單目標優化，并不是獲取一個目標的最優解，由于多目標函數的相互沖突，使得Pareto解未必占優。但如果單純優化一個目標，就會使得其他性能很差。因此，同時對多個性能指標進行優化設計時，需要決策者權衡滿足不同要求的優化結果，合理選取設計參數的值。

5 結論

(1)以一種可實現5自由度的4-UPS-UPU并聯機器人機構為研究對象，建立其運動學模型及雅克比矩陣，考慮機構在運動空間內的運動學性能，并引入全域條件指標和全域梯度指標作為運動靈巧度的評價指標;

(2)采用柱坐標邊界極限搜索法求解工作空間的方法，求解了全域條件指標的數學模型;在建立優化目標、選擇設計變量、確定優化目標的基礎上，構建了4-UPS-UPU機構運動靈巧度多目標優化模型;

(3)基于多學科設計優化軟件Modefrontier對機構進行了多目標優化研究，采用實驗設計和粒子群優化算法對機構進行了優化，求得Pareto解，并從多組解中合理選擇了最優解，并合理確定了結構參數和優化參數，通過優化前后結果比較，機構運動性能得到增強，該文為并聯機構優化設計提供參考依據。

［1］PLITEA Nicolae，SZILAGHYI Andras，PISLA Doina．Kinematic Analysis of a New 5-DOF Modular Parallel Robot for Brachytherapy［J］．Robotics and Computer-Integrated Manufacturing，2015，31:70－80．

［2］LI Yangming，XU Qingsong．Kinematics and Inverse Dynamics Analysis for a General 3-RPS Spatial Parallel Mechanism［J］．Robotics，2005，23:219－229．

［3］陳修龍，高慶，趙永生．4-UPS-UPU并聯式坐標測量機的靈巧度研究［J］．計算機集成制造系統，2012，18(6):1200－1208．

［4］齊明．4-UPS/UPU5自由度并聯機構尺度綜合方法［J］．哈爾濱工業大學學報，2009，11(41):160－164．

［5］WU Wenqiang，GUAN Yisheng，LI Huaizhu，et al．Performance Analysis and Optimization of Serial Robots［C］．Proceeding of the 2012 IEEE international Conference on Robotics and Biomimetics，2012．

［6］SUN Tao，SONG Yiming，DONG Gang．Optimal Design of a Parallel Mechanism with Three Rotational Degree of Freedom［J］．Robotics and Computer-Integrated Manufacturing，2012，28(4):500－508．

［7］李明磊，賈育秦，張學良，等．基于多目標差異演化算法的并聯機構結構優化［J］．中國機械工程，2010，21(16):1915－1920．

［8］陳修龍，賈帥帥，鄧昱，等．新型4-UPS-UPU并聯坐標測量機剛柔耦合動力學性態［J］．吉林大學學報:工學版，2011，41(4):1020－1024．

［9］GHOMMEM M，HAJJM R，MOOK D T B，et al．Global-Local Optimization of Flapping Kinematics in Hovering Flight［J］．International Journal of Micro Air Vehicles，2013，5(2):109－126．

［10］張彥斌，張海軍，吳鑫．新型純移動并聯機構的運動學和靈巧性分析［J］．機床與液壓，2010，38(15):13－16．

［11］LARA-MOLINA F A，ROSARIO J M，et al．Multi-Objective Design of Parallel Manipulator Using Global Indices［J］．The Open Mechanical Engineering Journal，2010，4:37－47．

［12］CUI Guohua，ZHANG Haiqiang，XU Feng，et al．Kinematics Dexterity Analysis and Optimization of 4-UPS-UPU Parallel Robot Manipulator［C］．Intelligent Robotics and Applications Lecture Notes in Computer Science，2014．

［13］JAMSHID Aghaei，KASHEM M Muttaqi，ALI Azizivahed，et al．Distribution Expansion Planning Considering Reliability and Security of Energy Using Modified PSO(Particle Swarm Optimization)algorithm［J］．Energy，2014，65:398－411．