桌式貼片機橫梁的模態分析及拓撲優化設計

白俊峰，閆俊存，黃 勇

BAI Jun-feng1, YAN Jun-cun1, HUANG Yong2

（1.長春工業大學 機電工程學院，長春 130012；2.吉林省博安消防設備有限公司，長春 130000）

0 引言

上世紀60年代，表面組裝技術 SMT（Surface Mounted Technology）就已經開始出現。經過幾十年的發展，SMT已經成為了一門涉及機械、電子、計算機以及材料等多門學科的綜合性技術。SMT的主要工作流程有點膠（或絲印）、貼裝、固化、回流焊（或波峰焊）、清洗、檢驗等工作流程。貼裝作為SMT中最主要的工序之一，精度要求極其嚴格，其工作任務主要由貼片機承擔。

貼片機實際上是一種高精度、高速度的智能機器人，主要由機械系統和控制系統組成。其中機械系統主要有機殼、XYZ三軸運動系統、貼片頭、機架、傳送機構等；控制系統主要有視覺識別系統、定位系統以及各種傳感器等。圖1所示為貼片機單次貼裝動作圖。

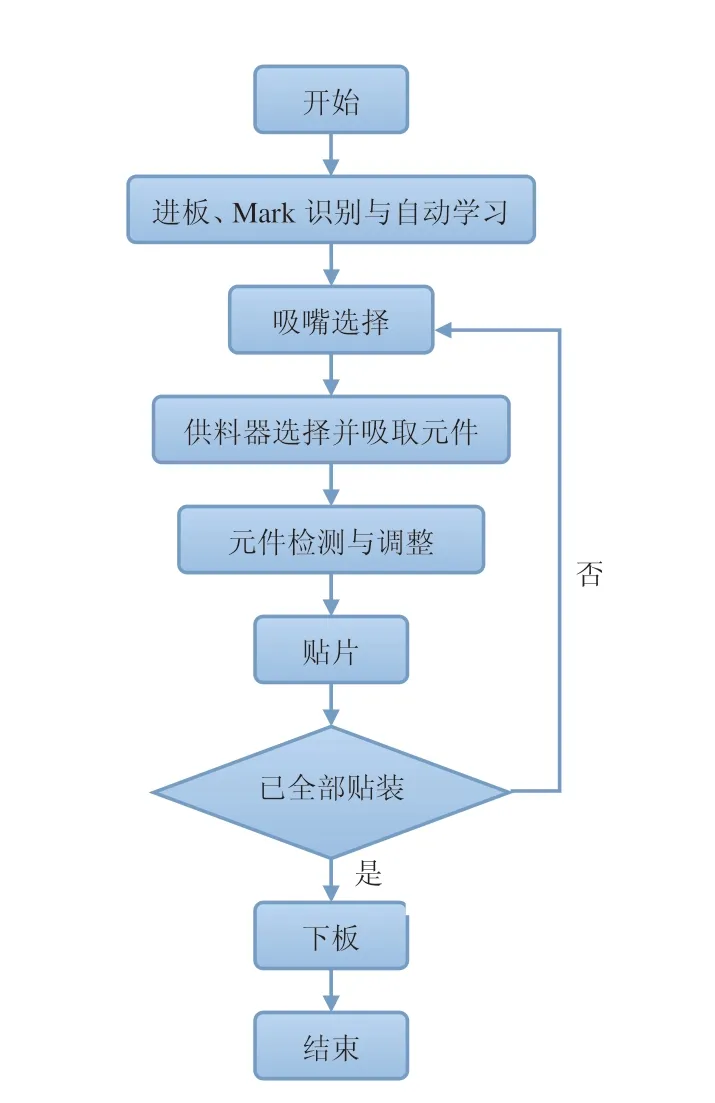
圖1 貼片機單次貼裝動作圖

1 桌式貼片機橫梁優化前有限元模型建立

橫梁承載著桌式貼片機XYZ軸的運動，它的結構直接影響貼片機的貼裝精度，是桌式貼片機最重要的構件之一。因此，貼片機貼裝精度能否滿足作業要求，與橫梁的結構設計、結構分析以及結構優化有著很密切的關系。本文主要采用有限元方法對橫梁結構進行模態分析，避免共振點；然后在此基礎上對橫梁結構進行拓撲優化，以保證貼片機貼裝精度。桌式貼片機的整機結構如圖2所示，其中橫梁采用鑄鋁成型如圖3所示。

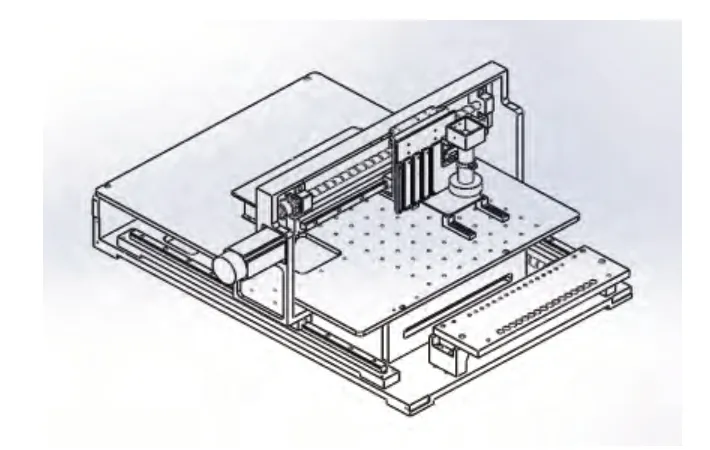
圖2 桌式貼片機的整機結構

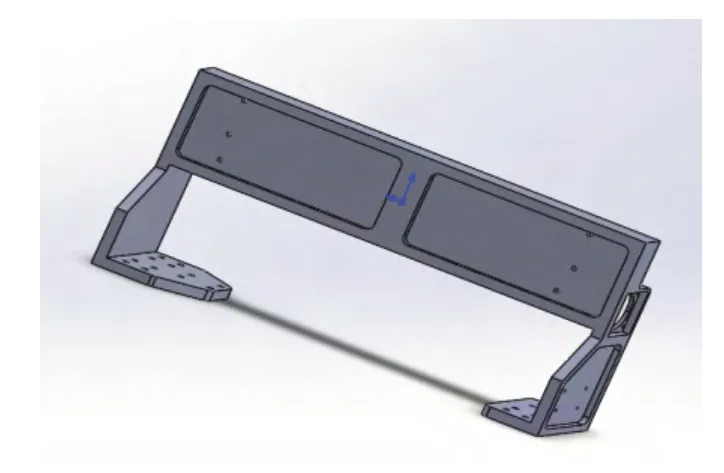
圖3 桌式貼片機橫梁

如上所述，橫梁作為貼片機的關鍵部件，其有限元模型的建立也是分析橫梁結構的關鍵環節，單元選擇不準確、模型大小與實際不相符，都會產生錯誤的分析結果。為保證計算精度、達到實際應用標準，本文采用ANSYS有限元法對橫梁進行分析，單元類型選用solid95實體單元，體積為：1.73×106mm3，質量為：4.7kg，楊氏模量：E=69GPa，泊松比為：0.33，材料密度為：2700kg/m3。網格劃分采用等級為6級的智能網格劃分，最終建立的有限元模型如圖4所示。

圖4 橫梁有限元模型

2 橫梁的模態分析

模態分析是工程中經常使用的分析方法，通過模態分析確定橫梁結構的固有振型和頻率，對橫梁進行合理改善，避開共振頻率；依據分析結果進行結構優化，優化結構應力集中部位，加強結構強度，延長結構使用壽命。

ANSYS有限元模態分析屬于線性分析，所有的非線性特性將被忽略，其主要理論基礎為振動理論分析方法。首先將模型結構進行網格劃分，將實體單元數據離散化處理；然后依據有限元數值分析方法，建立線性微分方程組；最后求出所構建方程組的特征值以及特征向量。根據振動理論相關知識，得到橫梁離散后的運動微分方程為：

式中[M]為橫梁結構的質量矩陣；[C]為阻尼矩陣；[K]為剛度矩陣；{U(t)}為位移向量；[F(t)]為激勵矩陣。

對式(1)進行拉氏變換，可得：

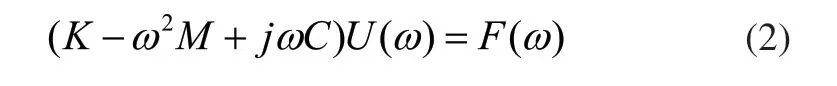
對于時不變線性系統某點的響應，可用各階模態響應的線性之和表示，于是可以得到某點a的響應為：

假設橫梁有限元模型中的M個節點第i階模態對應的振型系數組成的列向量為：則由這M個點所對應的全部模態振型系數矩陣為：

又設由這M個點組成的模態坐標矩陣為：

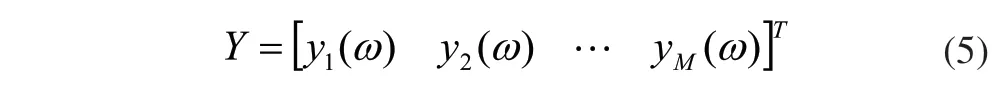
將式(4)、式(5)帶入式(3)，可以得到結構的響應向量為：

此時，可以將式(2)改寫為：

而在實際的模態分析中，阻尼對結構的固有頻率以及振型的影響很小，可以忽略不計，且ANSYS軟件測量結構的模態時一般不需要施加激勵，此時式(2)特征方程為：

這樣便可以求得橫梁的固有頻率計算公式：

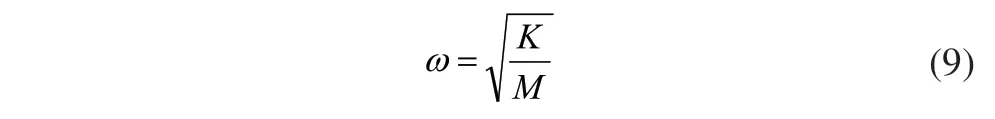
根據上面的計算原理，將上節建立的有限元模型載入ANSYS軟件，計算橫梁的前五階模態頻率及振型如表1所示，得到振型圖如圖5(a)～圖5(e)所示。

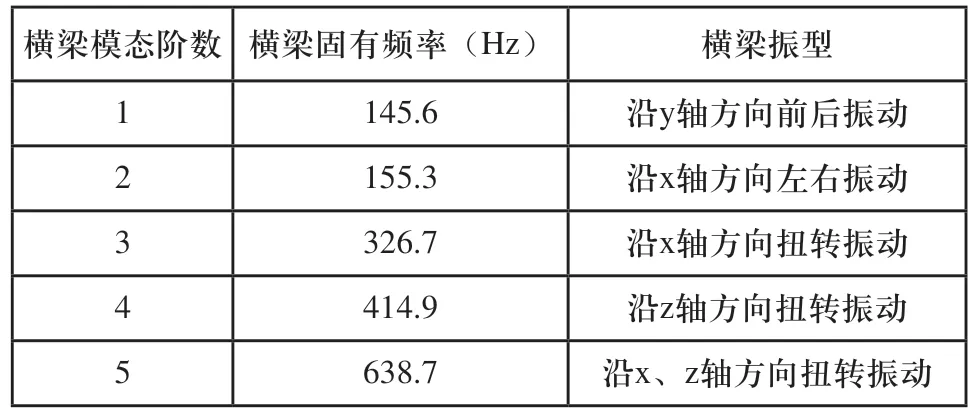
表1 橫梁前5階固有頻率及振型

通過表1數據可以看出，橫梁的一階固有頻率為145.6Hz，而系統所使用的伺服電機工作轉速變化范圍為0～3000r/min，即激勵系統的工作頻率變化范圍為0～50Hz，此橫梁結構固有頻率明顯大于激振頻率，故不會發生共振。但是由于此結構質量較大為4.7kg，在桌式貼片機高速運行突然急停進行貼片的動作中，橫梁的大質量引起的慣性作用，回使貼片頭在貼裝時發生偏移甚至可能出現錯位的現象，因此進行拓撲優化，對橫梁進行輕量化設計是非常必要的。

3 橫梁的拓撲優化設計

拓撲優化設計是運用優化設計理論、數據處理方法、計算機輔助軟件等工具，尋求材料最合理分配的一種設計理念，以達到結構最佳外觀形式、最佳受力途徑、結構最佳性能、結構最為輕量化的設計方法。

拓撲優化主要有三種方法：均勻法、變厚度法和密度懲罰法。本文中采用密度懲罰法來完成橫梁的拓撲優化，其數學模型如下：

式(10)中 iρ 為單元相對密度；f為結構體積力；u為單元相對面積力；v0為結構初始定義體積；v*為刪除的材料體積；Δ為刪除材料質量所占比例；ε為密度懲罰法材料密度下限；Jj為優化后密度保持最初狀態的單元。經過ANSYS拓撲優化計算，可以得到優化后單元密度變化情況如圖6所示，橫梁優化最終拓撲結構如圖7 所示。

圖6 優化單元密度變化圖

圖7 優化后拓撲結構

經測量，優化后計算得到橫梁的質量為3.8kg，比優化前減少了19.1%，減小了慣性帶來的貼裝誤差。

在實際的工程應用中，高階模態對結構的影響很小，因此本文僅對橫梁前五階模態進行了模態分析，得出優化后橫梁前五階模態固有頻率，以及優化后前兩階橫梁應力圖（優化后橫梁模態固有頻率與優化前的固有頻率對比如表2所示，優化后前兩階應力分布圖如圖8、圖9所示）。

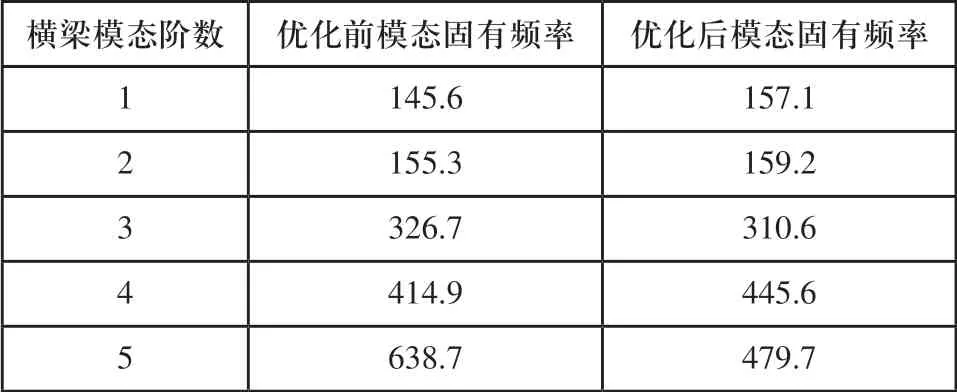
表2 拓撲優化前后固有頻率對照表

圖8 優化后橫梁1階應力圖

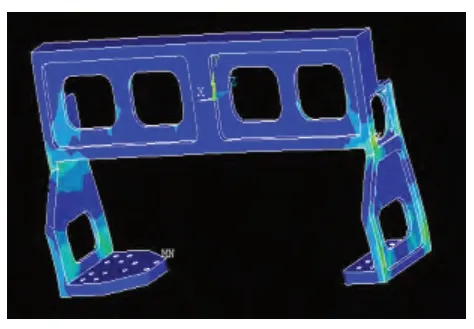
圖9 優化后橫梁2階應力圖

由表2可以看出，優化后1階、2階固有頻率有所提高，說明優化后結構剛度更大，橫梁在整個系統中更可靠；由圖8、圖9所得前兩階應力圖可以看出，優化后橫梁應力分布較為均勻，沒有出現應力集中部位。經測試，橫梁可以穩定承載桌式貼片機的整機運行，充分證實了以上分析結果。

4 結束語

通過ANSYS軟件分析了桌式貼片機橫梁的固有頻率和振型，并在此基礎上對橫梁結構進行了拓撲優化，以此種分析設計方法得到了一款結構更加穩定、更加輕量化、更加契合與桌式貼片機的機械運動系統。這樣不僅為貼片機的設計改進工作提供了參考，也為將來高精度儀器的設計提供了新的設計方法。

[1] 陳曄昕.電梯印板無鉛焊接研究[D].上海交通大學,2007.

[2] 盧利平.載貨汽車車架拓撲優化設計及有限元分析[D].合肥工業大學,2009.

[3] 胡世軍,梁東旭,張代錄,王瑞哲,袁銘.基于ANSYS的主軸箱體模態分析及拓撲優化[J].機械制造,2012.

[4] 德瑞西斯(德).機器動力學[M].科學出版社有限責任公司,2011.

[5] H.P. Mlejnek,R.Schirrmacher. An engineer’s approach to optimal material distribution and shape finding[J].Computer Methods Apppl, Mech Engrg.1993.

[6] Kirsch U and Topping B.H.V. Minimum Weight Design of Structural Topologies[J].J.Structural Eng.1992.

[7] Dr. Martin P. Bendsoe Optimization of structural topology[J].Shape and Material Springer-Verlag Berlin Heidelberg,1995.