有界控制導(dǎo)彈隨機(jī)最優(yōu)制導(dǎo)律①

花文華，孟慶齡，張金鵬，2

(1.中國(guó)空空導(dǎo)彈研究院，洛陽(yáng) 471009；2.航空制導(dǎo)武器航空科技重點(diǎn)實(shí)驗(yàn)室，洛陽(yáng) 471009)

?

有界控制導(dǎo)彈隨機(jī)最優(yōu)制導(dǎo)律①

花文華1，孟慶齡1，張金鵬1，2

(1.中國(guó)空空導(dǎo)彈研究院，洛陽(yáng) 471009；2.航空制導(dǎo)武器航空科技重點(diǎn)實(shí)驗(yàn)室，洛陽(yáng) 471009)

為削弱加速度界和系統(tǒng)噪聲對(duì)攔截導(dǎo)彈性能的影響，基于隨機(jī)控制理論，設(shè)計(jì)了一種考慮有界控制的隨機(jī)最優(yōu)制導(dǎo)律(stochastic optimal guidance law，SOGL)。通過(guò)系統(tǒng)降階與性能指標(biāo)變換和隨機(jī)輸入描述函數(shù)近似，將攔截導(dǎo)彈的控制有界和狀態(tài)估計(jì)誤差考慮到了該制導(dǎo)律的設(shè)計(jì)當(dāng)中。同時(shí)，為削弱目標(biāo)加速度估計(jì)延遲的影響，提出了一種SOGL的補(bǔ)償形式，并基于Monte Carlo方法進(jìn)行了仿真驗(yàn)證。結(jié)果表明，SOGL相比于傳統(tǒng)的最優(yōu)制導(dǎo)律性能得到了明顯改善，而其補(bǔ)償形式削弱了濾波器估計(jì)延遲的影響，更適用于目標(biāo)機(jī)動(dòng)存在切變的情形。

制導(dǎo)律；隨機(jī)控制；有界控制；目標(biāo)攔截

0 引言

有界控制是導(dǎo)彈制導(dǎo)系統(tǒng)設(shè)計(jì)中需要加以考慮的重要內(nèi)容。基于線性二次型性能指標(biāo)的制導(dǎo)方法，由于目標(biāo)機(jī)動(dòng)和量測(cè)噪聲的影響，在制導(dǎo)末端往往要求較強(qiáng)的機(jī)動(dòng)性能，如果不加以有效控制將直接影響最終的制導(dǎo)精度。傳統(tǒng)的制導(dǎo)律和估計(jì)器設(shè)計(jì)方法大多基于確定性等價(jià)原理[1]，二者分別針對(duì)完全信息情形和非完全信息情形獨(dú)立優(yōu)化，而在實(shí)際執(zhí)行中，為考慮有界控制，直接將由估計(jì)狀態(tài)所構(gòu)建的控制命令加以飽和約束，所得到的最終結(jié)果并不是最優(yōu)的。文獻(xiàn)[2]正是采用了這一設(shè)計(jì)思路給出了一種有界控制制導(dǎo)律。文獻(xiàn)[3-4]基于廣義分離原理，將估計(jì)結(jié)果的概率密度函數(shù)考慮到制導(dǎo)律的設(shè)計(jì)當(dāng)中，分別針對(duì)非線性和近似線性攔截情形，設(shè)計(jì)了相應(yīng)的飽和最優(yōu)制導(dǎo)律，但是該類型制導(dǎo)律包含較為復(fù)雜的數(shù)學(xué)計(jì)算，特別是涉及到末端狀態(tài)已知的時(shí)變Riccati微分方程組的求解，工程上較難實(shí)現(xiàn)。

本文考慮攔截導(dǎo)彈具有有界控制的非完全信息情形，通過(guò)適當(dāng)?shù)南到y(tǒng)模型和性能指標(biāo)轉(zhuǎn)換，設(shè)計(jì)一種有界控制隨機(jī)最優(yōu)制導(dǎo)律，并不涉及到復(fù)雜的數(shù)學(xué)計(jì)算問(wèn)題，更易于實(shí)際執(zhí)行，同時(shí)考慮濾波器估計(jì)延遲的影響，給出一種改進(jìn)形式。

1 問(wèn)題描述及建模

1.1 彈目相對(duì)運(yùn)動(dòng)關(guān)系數(shù)學(xué)描述

制導(dǎo)末端攔截導(dǎo)彈和目標(biāo)的相對(duì)運(yùn)動(dòng)關(guān)系如圖1所示。圖中，X軸沿初始視線方向；下標(biāo)m和t分別表示二者的相關(guān)狀態(tài)；q為視線角；r表示攔截導(dǎo)彈和目標(biāo)之間的相對(duì)距離；二者相對(duì)于初始視線方向的位移為y。

圖1 平面相對(duì)運(yùn)動(dòng)關(guān)系Fig.1 Planer engagement geometry

基于下述假設(shè)進(jìn)行問(wèn)題的研究：

(1)攔截導(dǎo)彈和目標(biāo)可視為質(zhì)點(diǎn)，并可沿初始視線方向?qū)崿F(xiàn)近似線性化；

(2)二者速度大小不變，近似具有一階控制系統(tǒng)或自動(dòng)駕駛儀動(dòng)態(tài)；

(3)攔截導(dǎo)彈可對(duì)相對(duì)運(yùn)動(dòng)關(guān)系和自身的相關(guān)狀態(tài)進(jìn)行噪聲下的量測(cè)，目標(biāo)無(wú)法獲取導(dǎo)彈的相關(guān)信息，但可意識(shí)到攔截企圖，從而隨機(jī)規(guī)避機(jī)動(dòng)。

考慮攔截導(dǎo)彈的有控制性并基于上述假設(shè)條件，選取狀態(tài)變量為x=[yvatam]T，則系統(tǒng)狀態(tài)方程可以近似表示為

(1)

其中

式中ωm、ωt為相互獨(dú)立的零均值高斯白噪聲；σm、σt分別為標(biāo)準(zhǔn)方差；τm、τt分別為攔截導(dǎo)彈和目標(biāo)的控制系統(tǒng)時(shí)間常數(shù)；amc、atc為相應(yīng)的控制命令；sat()表示飽和函數(shù)。

基于假設(shè)(1)和假設(shè)(2)，攔截導(dǎo)彈飛行時(shí)間為

tf=r0/Vc

(2)

式中r0為彈目初始距離；Vc為接近速度，近似為(Vm+Vt)。

剩余飛行時(shí)間可表示為

tgo=tf-t

(3)

1.2 量測(cè)方程

結(jié)合圖1，采用一定的彈上設(shè)備，如導(dǎo)引頭可對(duì)相對(duì)距離r、視線角q進(jìn)行量測(cè)。假設(shè)r是可精確量測(cè)的，q具有一定的量測(cè)噪聲，并且假設(shè)噪聲為白噪聲且符合高斯分布，標(biāo)準(zhǔn)方差為σq，則量測(cè)方程可表示為

z=Hx+vq

(4)

式中H=[1/r0 0 ]；vq為量測(cè)噪聲。

2 估計(jì)器和制導(dǎo)律設(shè)計(jì)

2.1 系統(tǒng)降階

定義線性二次型性能指標(biāo)：

(5)

式中G=diag(g，0，0，0)；g為加權(quán)系數(shù)，一定程度上體現(xiàn)了導(dǎo)彈攔截性能和機(jī)動(dòng)性能之間的折中。

基于式(1)所示的隨機(jī)狀態(tài)方程和性能指標(biāo)(5)推導(dǎo)攔截導(dǎo)彈制導(dǎo)律，必然會(huì)涉及到終端條件已知的Riccati方程組求解，為避免這一過(guò)程，本文采用了系統(tǒng)降階變換的設(shè)計(jì)方法。文獻(xiàn)[5]提出了一種稱為終端投影變換的系統(tǒng)降階方法，采用零效脫靶量Z作為新的狀態(tài)變量，以降低系統(tǒng)的維度。結(jié)合式(1)，可求得

(6)

其中

θm=tgo/τm

θt=tgo/τt

ψ(k)=exp(-k)+k-1

將式(6)兩邊對(duì)t求導(dǎo)：

(7)

系統(tǒng)被降階為以零效脫靶量作為狀態(tài)變量的形式，當(dāng)t=tf時(shí)，由式(6)可得到Z(tf)=y(tf)，因此性能指標(biāo)可進(jìn)一步轉(zhuǎn)化為

(8)

這一降階過(guò)程并不涉及到近似變換，可適用于攔截導(dǎo)彈存在飽和非線性控制特性的情形，下文還將進(jìn)行進(jìn)一步的轉(zhuǎn)換。

2.2 估計(jì)器設(shè)計(jì)

根據(jù)廣義分離原理，估計(jì)器可獨(dú)立于控制器進(jìn)行設(shè)計(jì)。降階后的系統(tǒng)以零效脫靶量作為狀態(tài)變量，估計(jì)器需要對(duì)這一狀態(tài)實(shí)現(xiàn)估計(jì)，因此結(jié)合系統(tǒng)(1)和量測(cè)方程(4)，Kalman濾波器的狀態(tài)變量進(jìn)一步定義為z=[Z(t)vatamatc]T，則狀態(tài)方程可以表示為

(9)

其中

本文主要應(yīng)用成型濾波器[6]方法表示目標(biāo)的隨機(jī)機(jī)動(dòng)策略，采用隨機(jī)輸入驅(qū)動(dòng)系統(tǒng)，wtc是標(biāo)準(zhǔn)方差為σtc的白噪聲過(guò)程。相應(yīng)的量測(cè)方程轉(zhuǎn)化為

y=Hzz+vq

(10)

其中

(11)

則Kalman濾波方程可表示為

(12)

E(η(t)η(τ))=Rδ(t-τ)

(13)

式中δ(t-τ)是Dirac函數(shù)。

Kalman濾波增益為

(14)

其中，P滿足以下Riccati微分方程：

(15)

式中Q為過(guò)程噪聲協(xié)方差陣；P(0)=E(z(0)zT(0))。

2.3 隨機(jī)最優(yōu)制導(dǎo)律推導(dǎo)

性能指標(biāo)(8)可進(jìn)一步表示為

(16)

(17)

結(jié)合式(12)，sat(amc)通過(guò)Kalman方程只對(duì)估計(jì)值產(chǎn)生作用，與估計(jì)誤差無(wú)關(guān)，因此制導(dǎo)律的設(shè)計(jì)只需要對(duì)性能指標(biāo)JZ進(jìn)行優(yōu)化。

將式(12)展開(kāi)，可得

(18)

(19)

式中K1和K5分別對(duì)應(yīng)K的第1和第5個(gè)元素。

雖然進(jìn)行了一定的轉(zhuǎn)換，式(17)和式(18)所表示的非線性優(yōu)化問(wèn)題，仍無(wú)法通過(guò)一般的方法進(jìn)行求解。為便于問(wèn)題的求解，給出一個(gè)假設(shè)條件。

比例導(dǎo)引、擴(kuò)展比例導(dǎo)引及最優(yōu)制導(dǎo)律等典型制導(dǎo)方法在表達(dá)形式上可歸結(jié)為一種統(tǒng)一的形式：

(20)

式中N為導(dǎo)航增益。

本文假設(shè)最終所得到的制導(dǎo)律具有如式(20)所示的典型形式，問(wèn)題進(jìn)一步轉(zhuǎn)化為導(dǎo)航增益的設(shè)計(jì)問(wèn)題，以降低求解的復(fù)雜性。參考文獻(xiàn)[4，7]，并采用隨即輸入描述函數(shù)(random input description function， RIDF)近似飽和函數(shù)，則式(18)可進(jìn)一步表示為

(21)

其中

(22)

基于上述假設(shè)和近似，由式(17)可得

(23)

(24)

(25)

制導(dǎo)律的設(shè)計(jì)最終轉(zhuǎn)化為狀態(tài)方程式(24)約束下針對(duì)性能指標(biāo)式(23)的優(yōu)化問(wèn)題。由此，構(gòu)造Hamiltonian函數(shù)，可以得到：

(26)

式中λ為L(zhǎng)agrange乘子。

由于N表示導(dǎo)航增益且相對(duì)于H是二次的，因此可求得N的最小值為

(27)

進(jìn)一步由協(xié)態(tài)方程和橫截條件可得

(28)

代入式(27)，可求得制導(dǎo)增益為

(29)

從而，所設(shè)計(jì)的隨機(jī)最優(yōu)制導(dǎo)律(stochastic optimal guidance law，SOGL)可表示為

(30)

該制導(dǎo)律通過(guò)系統(tǒng)降階和性能指標(biāo)變換，考慮到了導(dǎo)彈的有界控制性和狀態(tài)估計(jì)誤差的影響。

2.4 制導(dǎo)律的進(jìn)一步改進(jìn)

由上節(jié)的推導(dǎo)過(guò)程可看出，狀態(tài)估計(jì)誤差的概率密度函數(shù)已經(jīng)被間接考慮到制導(dǎo)律的優(yōu)化過(guò)程當(dāng)中，可改善制導(dǎo)精度。但是，估計(jì)器的引入會(huì)帶來(lái)一個(gè)明顯的問(wèn)題就是估計(jì)延遲，因此為進(jìn)一步改進(jìn)導(dǎo)彈的攔截性能，應(yīng)要求估計(jì)誤差方差和估計(jì)延遲同時(shí)的最小化，但這2種要求是存在矛盾的。一種可行的制導(dǎo)方案是將估計(jì)延遲因素也考慮到制導(dǎo)律的設(shè)計(jì)當(dāng)中，采用補(bǔ)償或者自適應(yīng)帶寬等方式，實(shí)現(xiàn)估計(jì)器估計(jì)誤差方差和估計(jì)延遲的設(shè)計(jì)折中，從而改進(jìn)攔截性能。

目標(biāo)加速度估計(jì)延遲對(duì)攔截性能的影響最為明顯，本文給出一種針對(duì)目標(biāo)加速度估計(jì)值的直接補(bǔ)償方法。將由估計(jì)延遲產(chǎn)生的目標(biāo)加速度可達(dá)集(不確定集)的中心值代替目標(biāo)加速度估計(jì)值，下面給出具體的推導(dǎo)過(guò)程。

由式(1)可得

at(t)=exp(-δ/τt)at(t-δ)+

(31)

(32)

(33)

因此，對(duì)于具有延遲的目標(biāo)加速度有

[at(t)]min≤at(t)≤[at(t)]max

(34)

將at(t)采用由延遲產(chǎn)生的不確定集的中心值代替：

at(t)=([at(t)]min+[at(t)]max)/2

=at(t-δ)exp(-δ/τE)

(35)

因此，零效脫靶量可進(jìn)一步修正為

(36)

其中，δ對(duì)應(yīng)假設(shè)的目標(biāo)加速度估計(jì)延遲。采用這一零效脫靶量表達(dá)形式用于SOGL的相關(guān)計(jì)算。改進(jìn)后的形式采用CSOGL (Compensated SOGL)表示。由式(36)可得

3 仿真結(jié)果及分析

主要針對(duì)一類迎面末端攔截情形進(jìn)行了仿真研究，如圖1所示，γm(0)≈0，γt(0)≈0，其他仿真參數(shù)如表1所示，其中T為采樣時(shí)間。針對(duì)2種形式的目標(biāo)機(jī)動(dòng)進(jìn)行了制導(dǎo)律SOGL和CSOGL的驗(yàn)證和比較。仿真基于Monte Carlo法，并采用單發(fā)命中概率[8](single shot kill probability， SSKP)作為目標(biāo)攔截性能的衡量指標(biāo)。

表1 仿真參數(shù)Table 1 Simulation parameters

(1)“bang-bang”目標(biāo)機(jī)動(dòng)

具有隨機(jī)時(shí)間切換的“bang-bang”機(jī)動(dòng)被認(rèn)為是最優(yōu)的規(guī)避機(jī)動(dòng)形式[9-10]。假設(shè)目標(biāo)機(jī)動(dòng)命令切換時(shí)間為tsw，圖2為tsw=1.5 s情形下的目標(biāo)加速度估計(jì)，當(dāng)估計(jì)器具有足夠的收斂時(shí)間時(shí)，可實(shí)現(xiàn)目標(biāo)加速的較好估計(jì)。圖3(a)和圖3(b)分別為該情形下相應(yīng)于制導(dǎo)律SOGL的導(dǎo)航增益變化曲線和脫靶量曲線，可以看出，由于受到目標(biāo)機(jī)動(dòng)和量測(cè)噪聲的影響，導(dǎo)航增益峰值Nmax出現(xiàn)在制導(dǎo)末端，要求導(dǎo)彈具有較強(qiáng)的機(jī)動(dòng)性能，最終的脫靶量為0.580 7 m，具有較高的制導(dǎo)精度。

圖2 目標(biāo)加速度閉環(huán)估計(jì)，“bang-bang”機(jī)動(dòng)Fig.2 Close-loop estimation of target acceleration, bang-bang maneuver

(a)導(dǎo)航增益，SOGL

(b)脫靶量，SOGL

(a)脫靶量

(b)導(dǎo)航增益峰值，SOGL

圖5給出了在“bang-bang”目標(biāo)機(jī)動(dòng)情形下，SOGL和CSOGL的累積脫靶量分布情況，仿真中，兩者取相同的目標(biāo)機(jī)動(dòng)命令切換時(shí)間和隨機(jī)數(shù)產(chǎn)生器種子。可以看出，對(duì)于給定的SSKP，例如SSKP=0.95，采用制導(dǎo)律CSOGL 所要求的彈頭殺傷半徑小于SOGL，總體而言具有較好的攔截性能。

圖5 累積脫靶量分布：SOGL和CSOGLFig.5 Cumulative miss distance distribution: SOGL and CSOGL

(2)常值目標(biāo)機(jī)動(dòng)

最優(yōu)制導(dǎo)律(optimal guidance law,OGL)的推導(dǎo)基于目標(biāo)常值機(jī)動(dòng)的假設(shè)，為進(jìn)一步驗(yàn)證所設(shè)計(jì)的制導(dǎo)律的性能，假設(shè)目標(biāo)做常值機(jī)動(dòng)。圖6對(duì)3種制導(dǎo)律——OGL、SOGL和CSOGL的攔截性能進(jìn)行了比較，所設(shè)計(jì)的有界控制隨機(jī)最優(yōu)制導(dǎo)律SOGL相比于OGL具有明顯的性能優(yōu)勢(shì)，而CSOGL的性能則較差，更適用于目標(biāo)機(jī)動(dòng)命令存在切變而造成估計(jì)延遲的情形。

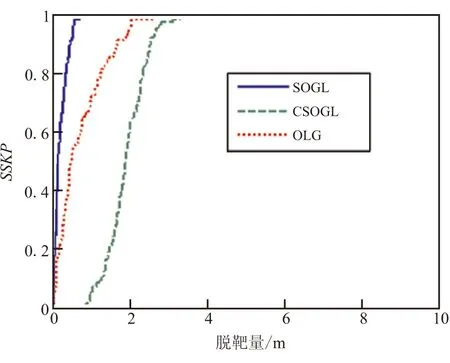
圖6 累積脫靶量分布：OGL、SOGL和CSOGLFig.6 Cumulative miss distance distribution: OGL,SOGL and CSOGL

4 結(jié)論

(1)SOGL將攔截導(dǎo)彈的有界控制性和狀態(tài)估計(jì)誤差直接考慮到制導(dǎo)律的設(shè)計(jì)當(dāng)中，為避免指令飽和，實(shí)現(xiàn)了彈道的及時(shí)調(diào)整，并削弱了濾波器估計(jì)誤差的影響，制導(dǎo)性能優(yōu)于最優(yōu)制導(dǎo)律。

(2)CSOGL在SOGL的基礎(chǔ)上進(jìn)一步考慮了濾波器估計(jì)目標(biāo)加速度延遲的影響，通過(guò)制導(dǎo)律的改進(jìn)設(shè)計(jì)，估計(jì)延遲的影響被有效削弱，因此更適用于目標(biāo)機(jī)動(dòng)存在切變的情形，該情形下的整體性能會(huì)優(yōu)于SOGL。

(3)SOGL和CSOGL在實(shí)現(xiàn)上并不涉及到復(fù)雜的數(shù)學(xué)計(jì)算，可適用于工程應(yīng)用。

[1] Shinar J,Shima T.Nonorthodox guidance law development approach for intercepting maneuvering targets[J].Journal of Guidance,Control and Dynamics,2002,25(4):658-666.

[2] 花文華,陳興林.變速導(dǎo)彈有界控制非線性微分對(duì)策制導(dǎo)律 [J].控制與決策,2011,26(12):1886-1890.

[3] Hexner G,Shima T.Stochastic optimal control guidance law with bounded acceleration [J].IEEE Transactions on Aerospace and Electronic Systems,2007,43(1):71-78.

[4] Hexner G,Shima T,Weiss H.LQG guidance law with bounded acceleration command [J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(1):77-86.

[5] Bryson E A,Ho C Y.Applied optimal control [M].Waltham,America:Blaisdell,1969:154-155.

[6] Zarchan P.Representation of realistic evasive maneuvers by the use of shaping filters [J].Journal of Guidance and Control,1979,2(1):290-295.

[7] G?kcek C,Kabamba P T,Meerkov S M.Disturbance rejection in control systems with saturating actuators [J].Nonlinear Analysis,2000,40(1-8):213-226.

[8] 花文華,陳興林,宋申民.基于多模型自適應(yīng)估計(jì)的混合策略微分對(duì)策制導(dǎo)[J].宇航學(xué)報(bào),2010,32(6):1582-1588.

[9] Shinar J,Steinberg D.Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model [J].Journal of Aircraft,1977,14(8):795-802.

[10] Shinar J,Turetsky V,Oshman Y.Integrated estimation/ guidance design approach for improved homing against randomly maneuvering targets [J].Journal of Guidance,Control,and Dynamics,2007,30(1):154-161.

(編輯：呂耀輝)

Stochastic optimal guidance law for bounded-control missiles

HUA Wen-hua1，MENG Qing-ling1，ZHANG Jin-peng1，2

(1.China Airborne Missile Academy,Luoyang 471009,China;2.Aviation Key Laboratory of Science and Technology on Airborne Guided Weapons,Luoyang 471009,China)

Based on stochastic control theory,a stochastic optimal guidance law(SOGL)considering bounded control was presented to weaken the effects of acceleration boundary and system noise of interception missiles.The control boundary and states estimation error were brought into design of the guidance law by use of system order reduction,performance index transformation and random-input description function approximation.To further reduce the effect of estimation delay,a compensated SOGL was proposed.Based on Monte Carlo method,simulations were carried out.As compared to traditional optimal guidance law,the simulation results show that the interception performance of SOGL is improved and the compensated SOGL weakens the effects of estimation delay of filter and is more suitable for target with switching maneuver.

guidance law;stochastic control;bounded control;target interception

2013-11-28；

：2014-02-24。

航空科學(xué)基金重點(diǎn)項(xiàng)目(20110112001)。

花文華(1983—)，男，博士，主要研究方向?yàn)轱w行器制導(dǎo)與控制。E-mail：huawh6611@163.com

V448

A

1006-2793(2015)01-0007-05

10.7673/j.issn.1006-2793.2015.01.002