廣義人體-結構-TMD耦合系統

周 叮 孫 昊 劉偉慶 李枝軍

(南京工業大學土木工程學院, 南京 211816)

廣義人體-結構-TMD耦合系統

周 叮 孫 昊 劉偉慶 李枝軍

(南京工業大學土木工程學院, 南京 211816)

研究了廣義人體-結構-TMD耦合系統的動力學特性．利用2段連續的直桿模擬靜立人體,將廣義人體和結構均簡化為單自由度,并與懸掛于結構下部的TMD共同組成一個三自由度的振動系統．推導出廣義人體-結構-TMD系統的無阻尼固有頻率、位移反應譜和加速度反應譜,并將結果與二自由度的結構-TMD系統進行對比．結果表明,廣義人體對系統的動力學特性具有一定的影響．當結構基頻為人體基頻的2倍時,這2個系統的無阻尼固有頻率差別較小;當結構基頻與人體基頻接近時,這2個系統的無阻尼固有頻率差別明顯．

廣義人體-結構-TMD系統;人體模型;耦合振動;動力學特性

隨著現代結構形式的不斷創新和高性能建筑材料的廣泛使用,人行橋、樓蓋正向著大跨、輕質、低阻尼的方向發展,結構更易受人群活動的影響而產生激振．因此,在進行結構設計時,應盡量避免結構的基頻落在人體運動激勵頻率的范圍內[1]．采用TMD技術抑制人行橋或樓蓋的振動是有效的解決方法之一[2-4]．

現實中,常會遇到部分人靜立于結構上而另一部分人在結構上行走或跳躍的情況,如人行橋上游客駐足觀光而行人則來去匆匆,歌舞廳中觀賞者靜立觀望而演員則跳舞演奏等．靜立人群會改變結構的動力學特性,行走人群則會激發結構產生振動．已有研究發現,當有人駐留于結構上時,系統的阻尼會相應增加,系統的基本頻率則有可能增加也有可能減少[5]．然而,目前使用的TMD減振設計規范并未考慮人體彈性對結構動力學性能的影響．

實驗研究和現場測試均表明,人體可等效為單自由度系統[6]．設計TMD時,人行橋和樓蓋等結構可簡化為單自由度系統,故靜立在結構上的人群、結構以及TMD一起構成了一個三自由度系統[7]．本文依據生物力學知識,使用2段連續的直桿模擬靜立人體,采用解析法研究人體彈性對系統動力學特性的影響．

1 耦合系統的微分方程

僅考慮人行橋或樓蓋的基階模態,利用能量等效原理,可將結構上的靜立人群等效為靜立在人行橋或樓蓋跨中處的廣義人體,從而得到用單自由度表述的人群簡化模型．

圖1為廣義人體-結構-TMD耦合系統.圖中,m(x),k(x),c(x)分別為廣義人體模型的分布質量、分布剛度和分布阻尼;h為人體高度．廣義人體靜立于單自由度結構上,結構的質量、剛度、阻尼分別為MS,KS,CS．結構受激勵力PS(t)作用,結構下部附有質量為MT、剛度為KT、阻尼為CT的單自由度TMD．僅考慮廣義人體的基階模態,忽略人體腳部彈性和阻尼的影響,即可得到具有三自由度的振動系統．

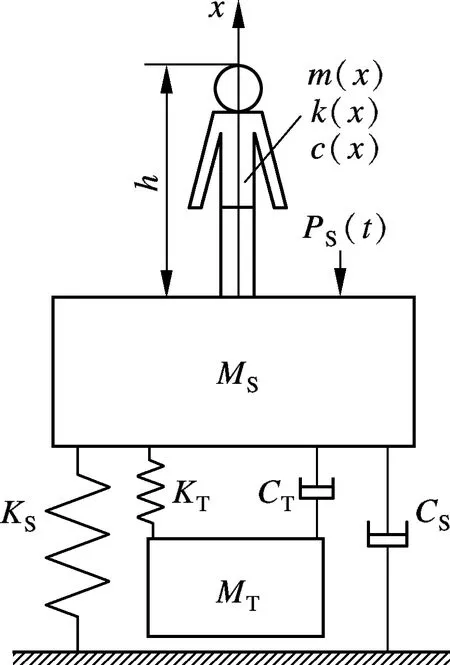
圖1 廣義人體-結構-TMD耦合系統

設結構位移為uS(t),廣義人體的基階模態坐標為uHR(t),TMD位移為uTMD(t),其中t為時間．

廣義人體位移uH(x,t)可表示為

uH(x,t)=uS(t)+uR(x,t)=uS(t)+uHR(t)φ(x)

(1)

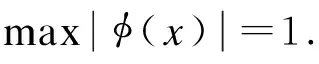
設結構、廣義人體和TMD的勢能分別為US,UH,UTMD,動能分別為TS,TH,TTMD,阻尼耗能分別為RS,RH,RTMD,則廣義人體-結構-TMD系統的勢能U、動能T和阻尼耗能R分別為

(2a)

(2b)

(2c)

激勵力所做的功為

W=PS(t)uS(t)

(2d)

系統受迫振動的拉格朗日方程為

(3)

將式(2)代入式(3),可得廣義人體-結構-TMD系統的微分方程為

(4)

式中

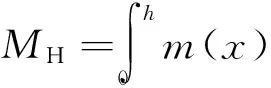
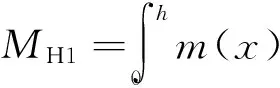
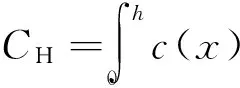
式中,MH0,MH,KH,CH分別為廣義人體總質量、基階模態質量、基階模態剛度和基階模態阻尼;MH1為廣義人體與結構的耦合質量．

若不考慮TMD對結構的作用,可將式(4)轉化為人體-結構系統的微分方程[8]．若不考慮廣義人體對結構動力學特性的影響,則將式(4)轉化為結構-TMD系統的微分方程,即

(5)

引入如下無量綱參數:

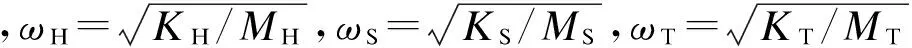
由此可將式(4)可改寫為

(6)

式(5)可改寫為

(7)

2 廣義人體的模態參數

根據生物力學知識,人體可用分段的連續直桿來模擬[6]．如圖2所示,本文使用簡單的2段連續直桿模型,并設每段人體的質量和剛度平均分布．圖中,mi,ki,xi,oi分別為第i(i=1,2)段直桿的質量、軸向剛度、坐標和坐標原點．

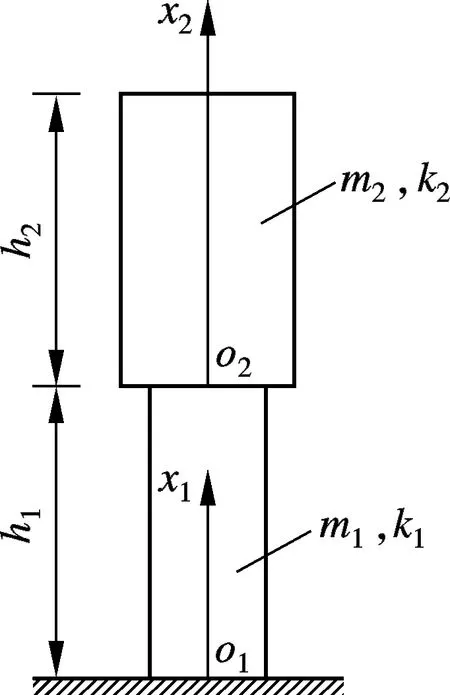
圖2 人體豎直方向的振動模型

[6,8],可得廣義人體的等效質量和參數為:MH1=0.765 9MH0,MH=0.666 7MH0,η=1.149,γ1=1.500α．

3 廣義人體-結構-TMD系統的無阻尼固有頻率

令ξS=ξH=ξT=PS(t)=0,由式(6)可得廣義人體-結構-TMD系統的無阻尼固有頻率特征方程為

(8)

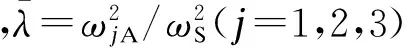
類似地,令ξS=ξT=PS(t)=0,由式(7)可得結構-TMD系統的無阻尼固有頻率方程為

l=1,2

(9)

當α=0.05時,廣義人體-結構-TMD系統和結構-TMD系統的無阻尼固有頻率曲線見圖3．由圖可知,當結構基頻為人體基頻的2倍(即β1=0.5)時,結構-TMD系統的第1頻率與廣義人體-結構-TMD系統的第2頻率接近,結構-TMD系統的第2頻率則與廣義人體-結構-TMD系統的第3頻率接近．當結構基頻與人體基頻相近(即β1=1.0)時,這2種系統的無阻尼固有頻率差別明顯．

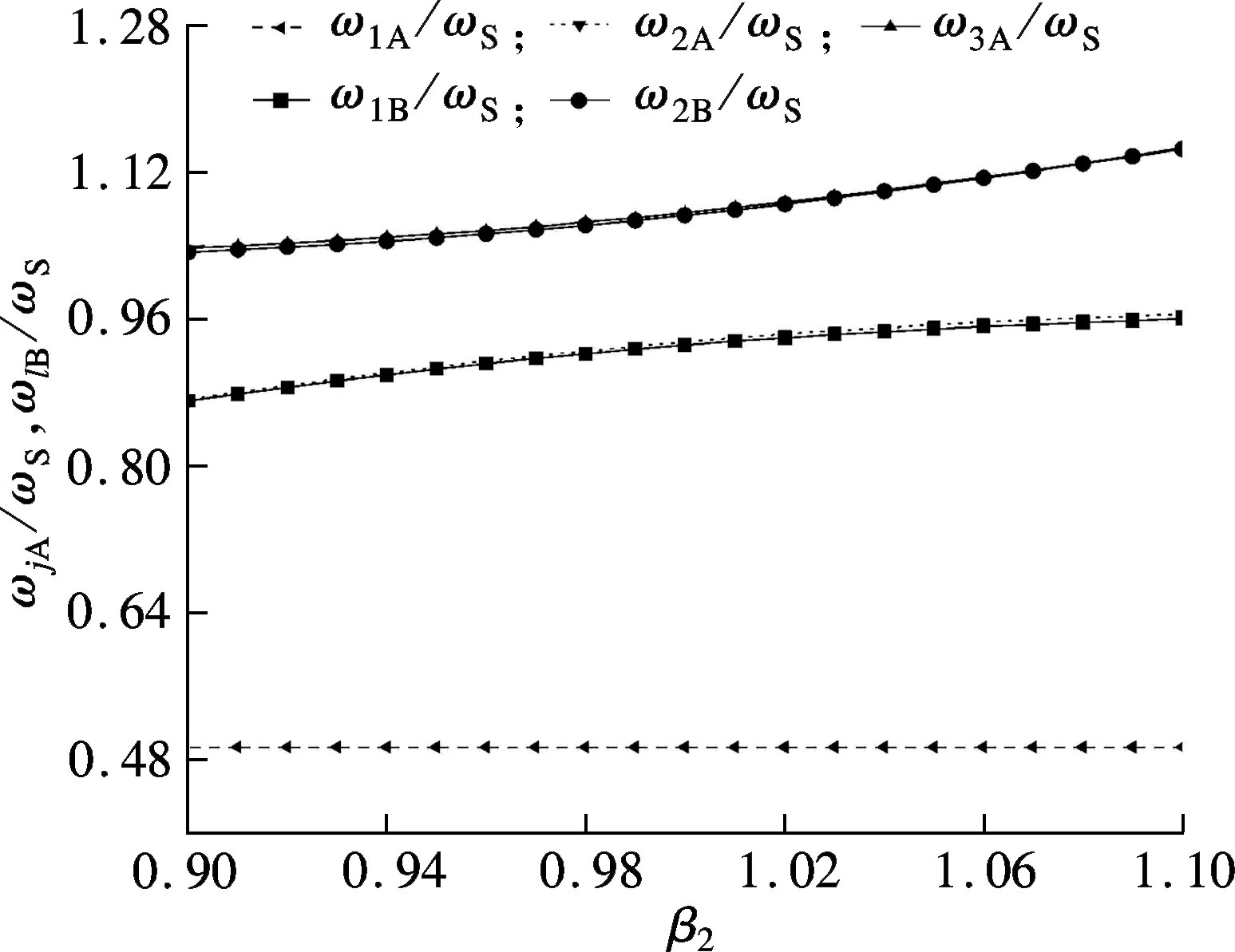
(a) β1=0.5,γ2=0.02

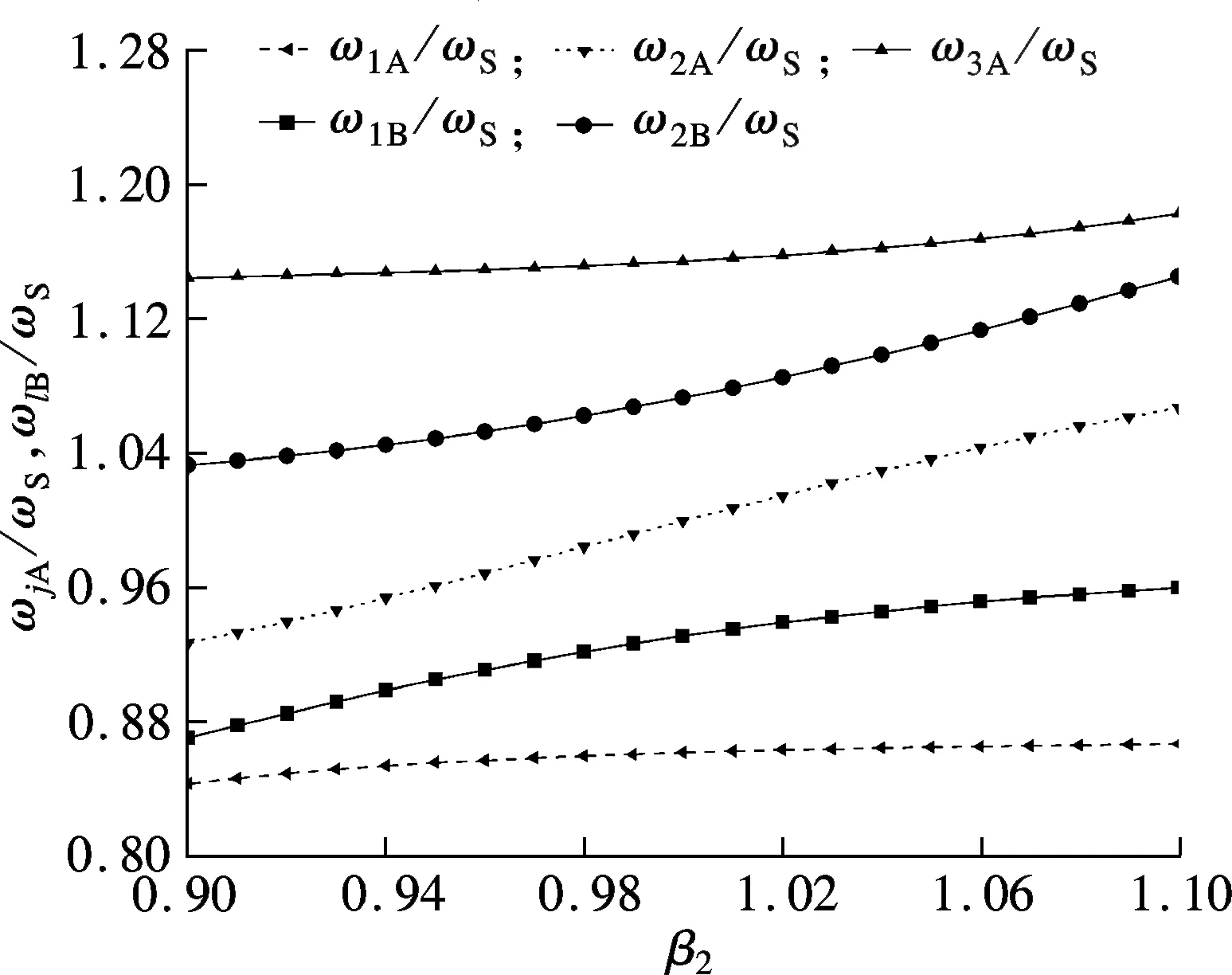
(b) β1=1.0,γ2=0.02

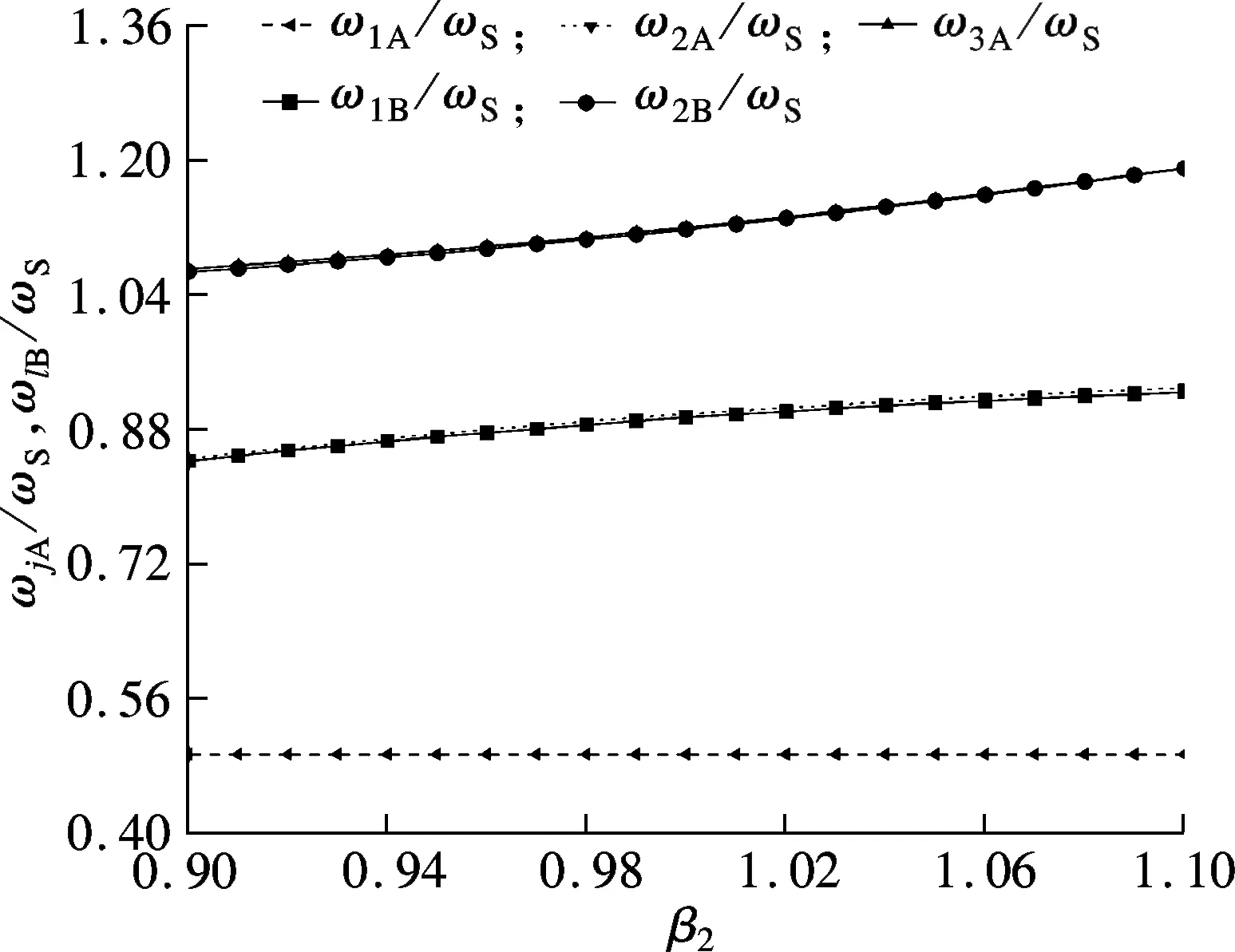
(c) β1=0.5,γ2=0.05

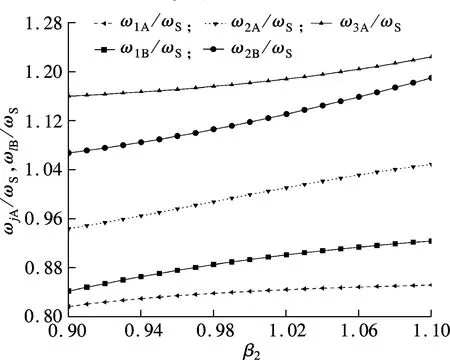
(d) β1=1.0,γ2=0.05

已知人體的基頻約為5 Hz[9],對比表1發現,隨著β2的增加,結構-TMD系統的第1頻率與廣義人體-結構-TMD系統的第1頻率差別逐漸增大,而結構-TMD系統的第2頻率與廣義人體-結構-TMD系統的第3頻率的差別則逐漸減小．TMD的減振效果僅在窄帶頻率范圍內較明顯．在此頻率范圍內,雖然人體彈性對系統基階頻率的影響較小,但TMD的減振效果仍會被減弱．

表1 不同情況下靜立人體彈性對頻率的影響(α=0.05,β1=1.0,γ2=0.05,ωS=ωH=10π)

4 廣義人體-結構-TMD系統的頻譜響應

對式(6)進行傅里葉變換可得

(10)

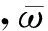
復頻反應函數為

(11)

式中

由此可得廣義人體-結構-TMD系統中結構和TMD的位移頻譜函數分別為

(12a)

(12b)

其結構的加速度頻譜函數為

(12c)

式中

E(λ)=2ξTβ2λ

F(λ)=2ξHβ1λ

N(λ)=-λ2

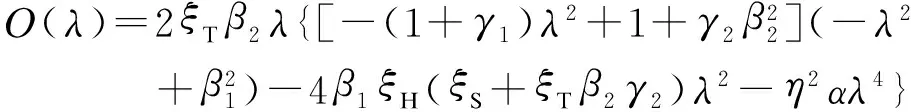
對式(7)進行傅里葉變換,可得結構-TMD系統中結構和TMD的位移頻譜函數分別為

(13a)

(13b)

其結構的加速度頻譜函數為

(13c)

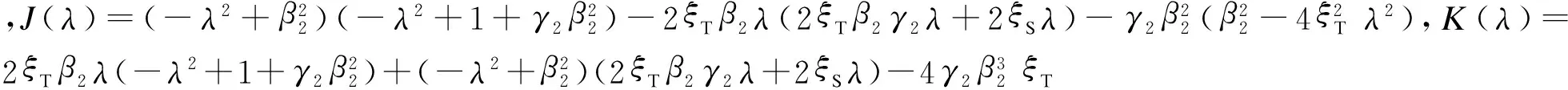
當β2=1.0,α=0.05,γ2=0.02,ξS=0.02,ξH=0.4,ξT=0.03時,廣義人體-結構-TMD系統與結構-TMD系統的頻域值比較見表2．由表可知,當β1=0.5,λ≤0.80時,廣義人體-結構-TMD系統中結構和TMD的響應均大于結構-TMD系統的響應;當β1=0.5,λ≥0.84時,結果則正好相反．當β1=1.0,λ≤0.88時,廣義人體-結構-TMD系統中結構和TMD的響應明顯大于結構-TMD系統的響應;當β1=1.0,λ≥0.92時,結果則正好相反．

5 結論

1) 當β1=0.5時,考慮和不考慮靜立人體的2個系統的無阻尼固有頻率接近．當β1=1.0時,2個系統的頻率差別較明顯．

2) 當β1=0.5,λ≤0.80時,廣義人體-結構-TMD系統中結構和TMD的響應均大于結構-TMD系統的響應;當β1=0.5,λ≥0.84時,結果則正好相反．當β1=1.0,λ≤0.88時,廣義人體-結構-TMD系統中結構和TMD的響應明顯大于結構-TMD系統的響應;當β1=1.0,λ≥0.92時,結果則正好相反．

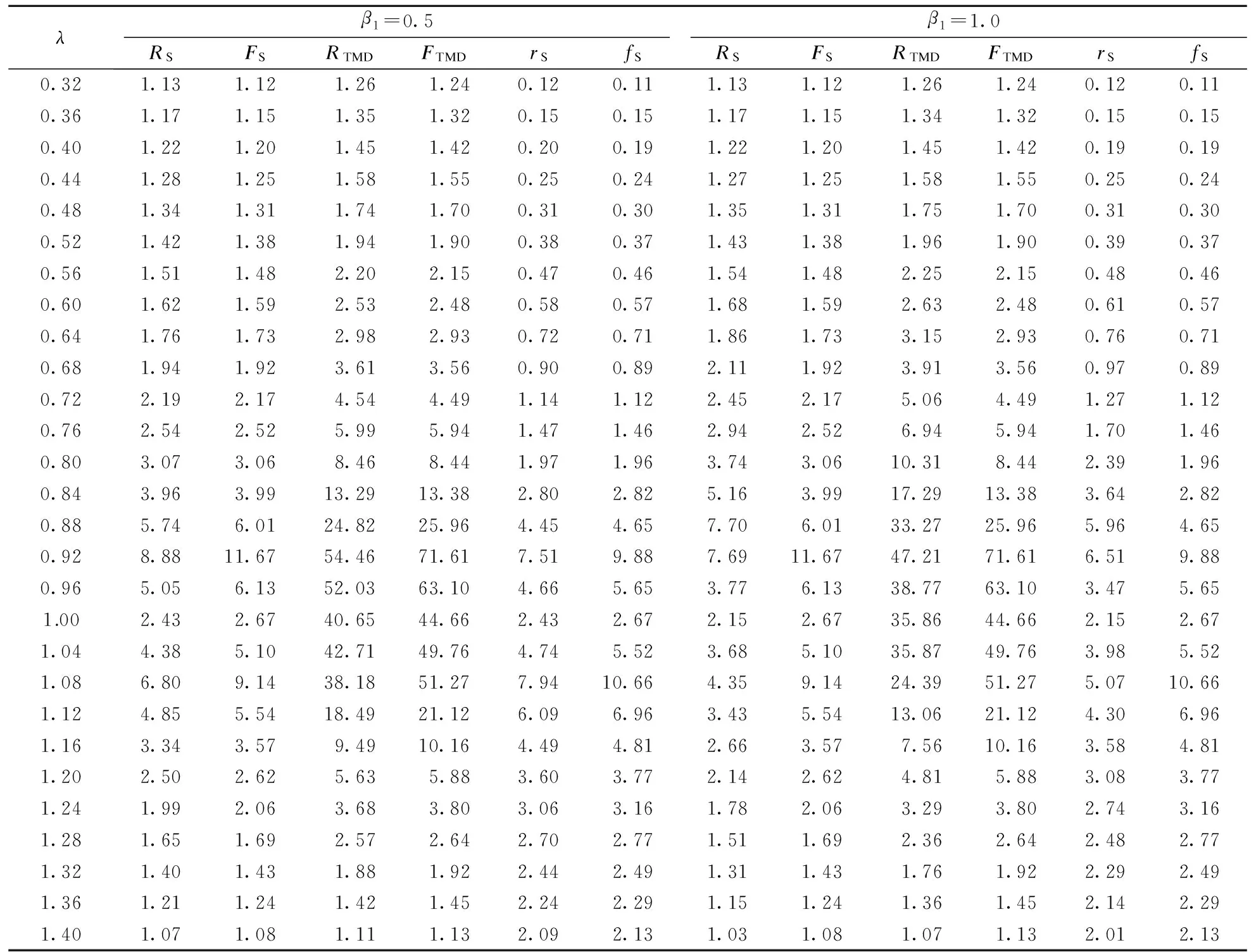
表2 廣義人體-結構-TMD系統與結構-TMD系統的頻域值

參考文獻 (References)

[1]孫利民, 閆興非. 人行橋人行激勵振動及設計方法[J]. 同濟大學學報:自然科學版, 2004, 32(8): 996-999. Sun Limin, Yan Xingfei. Human walking induced footbridge vibration and its serviceability design [J].JournalofTongjiUniversity:NaturalScience, 2004, 32(8): 996-999. (in Chinese)

[2]樊健生, 陳宇, 聶建國. 人行橋的TMD減振優化設計研究[J]. 工程力學, 2012, 29(9): 133-156. Fan Jiansheng, Chen Yu, Nie Jianguo. Optimum design of tuned mass damper for footbridge [J].EngineeringMechanics, 2012, 29(9): 133-156. (in Chinese)

[3]李愛群, 陳鑫, 張志強. 大跨樓蓋結構減振設計與分析[J]. 建筑結構學報, 2010, 31(6): 160-170. Li Aiqun, Chen Xin, Zhang Zhiqiang. Design and analysis on vibration control of long-span floor structures [J].JournalofBuildingStructures, 2010, 31(6): 160-170. (in Chinese)

[4]Setareh M, Ritchey J K, Baxter A J, et al. Pendulum tuned mass dampers for floor vibration control [J].JournalofPerformanceofConstructedFacilities, 2006, 20(1): 64-73.

[5]Falati S. The contribution of non-structural components to the overall dynamic behaviour of concrete floor slabs [D]. Oxford, UK: University of Oxford, 1999.

[6]Ji T,Ellis B R. A continuous model for the vertical vibration of the human body in a standing position [C]//UnitedKingdomInformalGroupMeetingonHumanResponsetoVibration. Silsoe, UK, 1995: 18-29.

[7]Ji Tianjian. Understanding the interactions between people and structures [J].TheStructuralEngineers, 2003, 81(14): 12-13.

[8]Zhou Ding, Ji Tianjian, Liu Weiqing. Dynamic characteristics of a standing human on a SDOF structure [J].AdvancesinVibrationEngineering, 2012, 11(1): 85-98.

[9]Matsumoto Y, Griffin M J. Dynamic response of the standing human body exposed to vertical vibration: influence of posture and vibration magnitude[J].JournalofSoundandVibration, 1998, 212(1): 85-107.

Generalized human-structure-TMD coupled system

Zhou Ding Sun Hao Liu Weiqing Li Zhijun

(College of Civil Engineering, Nanjing Tech University, Nanjing 211816, China)

The dynamic characteristics of the generalized human-structure-TMD (tuned mass damper) coupled system were studied. A continuous straight bar with two segments was used to model the static body. The generalized human and the structure were simplified as single-degree-of-freedom, and were combined with the TMD suspended under the structure to form a 3DOF (three-degree-of-freedom) vibration system. The undamped natural frequency, the displacement spectra and the acceleration spectra of the generalized human-structure-TMD system were derived. The comparison results between the 3DOF vibration system and the 2DOF (two-degree-of-freedom) structure-TMD system show that the generalized human-body has some effects on the dynamic characteristics of the system. When the fundamental frequency of the structure is twice that of the body, the difference of the undamped nature frequencies of these two systems is small. When the fundamental frequency of the structure is close to that of the body, the difference is considerable.

generalized human-structure-TMD (tuned mass damper) system; body model; coupled vibration; dynamic characteristics

10.3969/j.issn.1001-0505.2015.02.026

2014-08-11. 作者簡介: 周叮(1957—)，男，博士，教授，博士生導師，dingzhou57@yahoo.com.

國家自然科學基金資助項目(11372127).

周叮,孫昊,劉偉慶，等.廣義人體-結構-TMD耦合系統[J].東南大學學報:自然科學版,2015,45(2):348-353.

10.3969/j.issn.1001-0505.2015.02.026

TU399

A

1001-0505(2015)02-0348-06