一種基于IWOLA的脈沖星消色散數字終端設計

王顯海 孟 橋 張健偉 張添翼

(東南大學射頻與光電集成電路研究所, 南京 210096)

一種基于IWOLA的脈沖星消色散數字終端設計

王顯海 孟 橋 張健偉 張添翼

(東南大學射頻與光電集成電路研究所, 南京 210096)

在基于FPGA的脈沖星消色散數字終端中,為了解決片內高速RAM資源的系統設計瓶頸,提出了一種基于IWOLA算法的多相濾波器組(PFB),并基于該算法構建了一種針對寬帶實輸入信號的脈沖星消色散數字終端.該數字終端通過約簡多子帶進行處理.理論分析結果表明,該數字終端節省了系統對高速RAM和后續信號處理單元的需求,在保證時間分辨率的前提下提高了頻率分辨率.另外,該數字終端計算效率高,且克服了基于PDFT算法的系統設計缺陷.當脈沖星消色散終端中FFT模塊的長度為8 192時,基于IWOLA算法的脈沖星消色散數字終端最大節省了25%的BRAM資源.仿真實驗結果表明,該系統的性能滿足設計要求.

PDFT;IWOLA算法;FPGA;消色散

脈沖星是高速旋轉的中子星,在地球引力波、星際介質和脈沖星導航等研究領域具有重要意義.脈沖星信號在通過星際介質的傳播過程中會引起色散問題,需要對其進行消色散處理,這是脈沖星觀測中必不可少的一個重要環節,也是消耗硬件資源的一個核心部分.脈沖星觀測中用于非相干消色散的頻域數據主要來自于頻譜儀,因此,頻譜儀在脈沖星觀測中起著重要的作用.

脈沖星信號極其微弱,在觀測中要求系統具有盡可能寬的處理帶寬和高的時間或頻率分辨率.基于FFT的數字頻譜儀能較好地滿足這2個指標要求,根據實現算法的不同,可以將其分為基于組合復FFT算法的頻譜儀和基于多相濾波器組(PFB)的頻譜儀[1-3].前者結構較為復雜,對片上RAM資源占用較多[3];后者計算效率較高,尤其適合于寬帶信號的處理,它可以分為基于多相濾波器DFT(PDFT)算法和基于加權疊加(WOLA)算法的頻譜儀[4-5].基于PDFT算法的頻譜儀系統架構主要由多相濾波器組和FFT模塊組成.受FPGA內RAM的限制,一般用于實現1 024的幾倍到幾十倍級別的通道劃分.超高頻率分辨率的頻譜儀一般采用PFB和FFT兩級來實現,需要片外RAM進行大量數據緩存[6].WOLA算法是一種有效的頻帶劃分實現形式[7],具有低功耗的特點,解決了一般多相結構進行頻帶劃分時通道數與數據抽取率必須相同的限制問題,提高了系統的設計靈活性[8],近年來已廣泛應用于子帶編碼、OFDM、音頻信號處理和射電天文等領域[9-13].

本文提出了一種應用于寬帶實信號的IWOLA算法,并基于該算法構建了一種脈沖星消色散數字終端.這種數字終端能同時對寬頻帶內的多個子頻帶進行處理.另外,與基于組合復FFT算法和WOLA算法的頻譜終端相比,基于IWOLA算法的脈沖星數字終端更加節省FPGA的RAM資源.

1 IWOLA算法

基于PDFT算法的PFB推導是通過將數據抽取率等于PFB通道數來實現的,這限制了系統結構的靈活性.為了克服這一問題,文獻[14]提出了一種基于WOLA算法的PFB,它是PFB的一種有效實現形式[15],最初應用于短時傅里葉變換(STFT)中.STFT是指在FFT之前對數據進行加窗處理,其數學表達式為

(1)

式中,x(m)為輸入信號序列;w(n)為分析窗;y(n,ω)為短時傅里葉變換的輸出;n為當前時刻;m為求和變量;ω為歸一化的數字頻率.

令k1為0～K-1間的任意整數，v1為離散時間點，且k1=ωK/2π,v1=n/D,v1D-m=-q1,q1=l1K+p1.其中,D為數據抽取率;K為FFT的長度;l1為0～D-1間的任意整數；p1為通道序號.則基于WOLA算法的PFB數學表達式為[14-15]

式中,Rv1(p1)為加權疊加運算,它代替了PDFT算法中的卷積運算,且

l1=0,1,2,…,D-1

p1=0,1,2,…,K-1

v1=0,1,2,…,∞

(3)

利用圖1(a)中的子帶劃分方法,在式(2)所描述的PFB系統中實現了對信號頻帶的劃分.當輸入信號是帶寬為奈奎斯特采樣頻率一半的實信號時,需要處理K/2+1個通道數據.但鑒于實信號頻譜的對稱性,只需計算K/2個通道的數據即可.因此,對于實輸入信號,可以對WOLA算法進行改進,約減一個需要處理的子帶,節省一個后續處理的子系統資源.令Wk(ejω)為濾波器的頻率響應，如圖1所示,只要將各子通道的中心頻率沿X軸正方向平移π/K,便可減少一個后續處理的子系統.由此便可導出基于IWOLA算法的PFB.

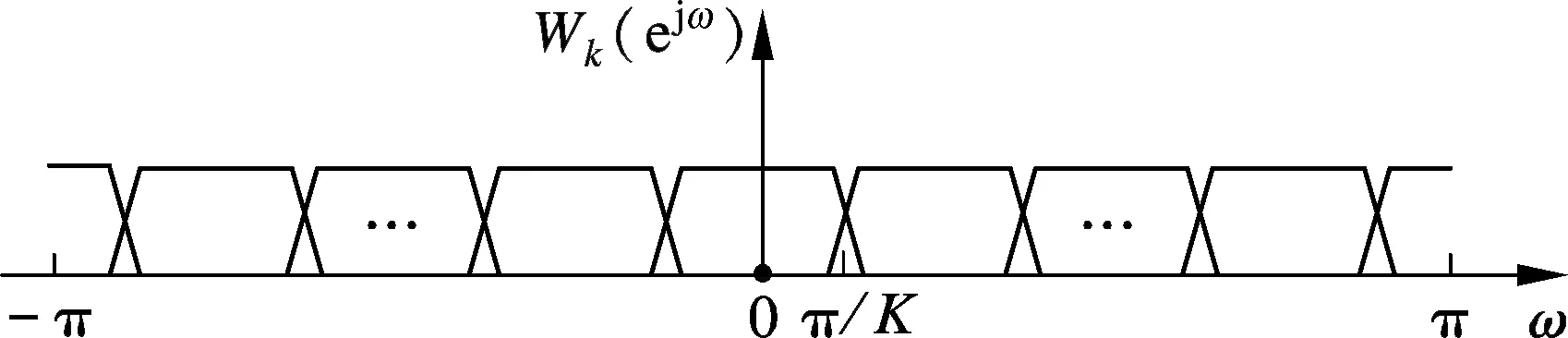
(a) 實信號通道的一般劃分方法

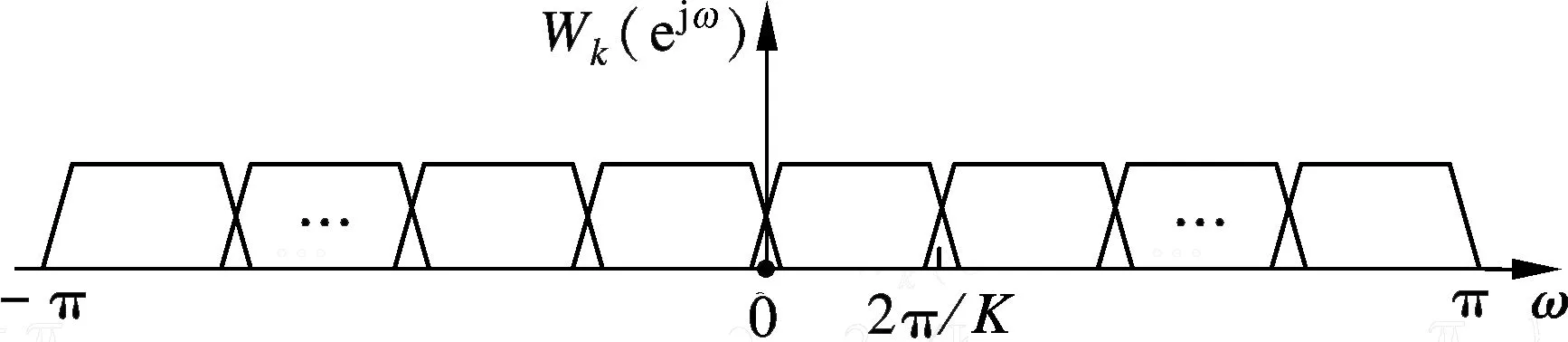
(b) 實信號通道經過搬移之后的劃分方法

令k=(ω-π/K)K/2π,式(1)可改寫為

(4)

假定v=n/D,vD-m=-q,q=lK+p,其中,k為0～K-1間的任意整數，v為離散時間點，l為0～D-1間的任意整數,可以得到

w(-q)e-j2πkq/Ke-jπvD/Ke-jπq/K=

w(-lK-p)e-j2πk(lK+p)/Ke-jπvD/Ke-jπ(lK+p)/K=

w(-lK-p)e-jπp/Ke-j2πkp/K=

(5)

式中

Fv(p)=Rv(p)e-jπp/K

l=0,1,2,…,D-1

p=0,1,2,…,K-1

v=0,1,2,…,∞

(6)

與式(2)相比,式(5)中多了2個指數項和1個(-1)l次方項.式(5)的計算過程見圖2.基于IWOLA算法的PFB的框架圖見圖3.

圖2 y(v,k)的計算過程

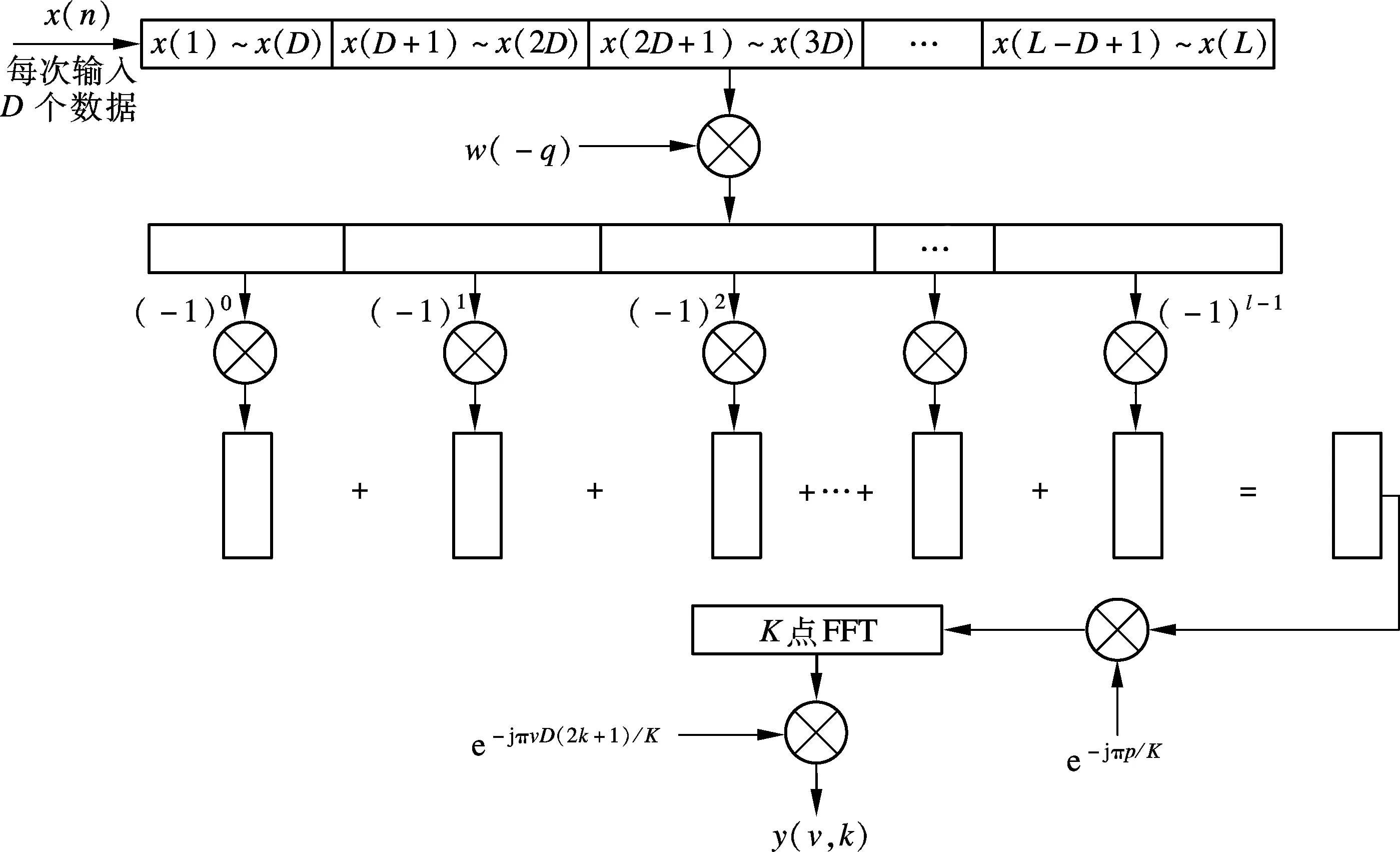
圖3 基于IWOLA算法的PFB框架圖

2 IWOLA算法的應用

將基于IWOLA算法的PFB應用于脈沖星消色散數字終端,可滿足同時對幾路數據進行消色散的應用要求,并較好地兼顧信號處理帶寬、頻率分辨率和時間分辨率的要求.系統框架如圖4所示.PFB的數據抽取率D=8,K=8,系統只需計算4個輸出通道的數據即可,每個通道的輸出都是復數數據.將1.2 GHz帶寬的實信號劃分為4個子帶,在保持每個子帶頻率分辨率的同時,提高了系統的時間分辨率.每個子通道的數據通過累加積分模塊后,根據需要輸出至不同的計算機,進行消色散處理.與組合復FFT算法的終端相比,基于IWOLA算法的脈沖星數字終端設計相對簡單.其設計過程既利用了IP Core的復數計算能力,又避免了組合復FFT算法中復數FFT到實數FFT數據解算的復雜處理過程.

圖4中的ADC工作于時鐘交錯模式,需要對時鐘相位和時延差異引起的增益誤差、偏置誤差和相位延遲誤差進行修正.實輸入信號經過ADC后轉換成高速數據流,其速率為2.4×109樣本/s，每個數據樣本寬度為8 bit;然后分成4路送入FPGA的數據接口模塊,完成數據的正確接收,每路數據速率為6×108樣本/s.數據接口模塊將4路數據流分成8路速率為3×108樣本/s的數據流,送入基于IWOLA算法的PFB中,完成信號頻帶劃分;然后,對輸出的4路復信號分別進行長度為8 192的FFT計算,每一路的頻譜分辨率為36.6 kHz.另外,將FFT模塊輸出的頻域數據經功率計算模塊后,送入積分模塊按時間進行疊加,從而提高了信號的信噪比,降低了數據輸出量.累加次數是由積分時間長度控制的.

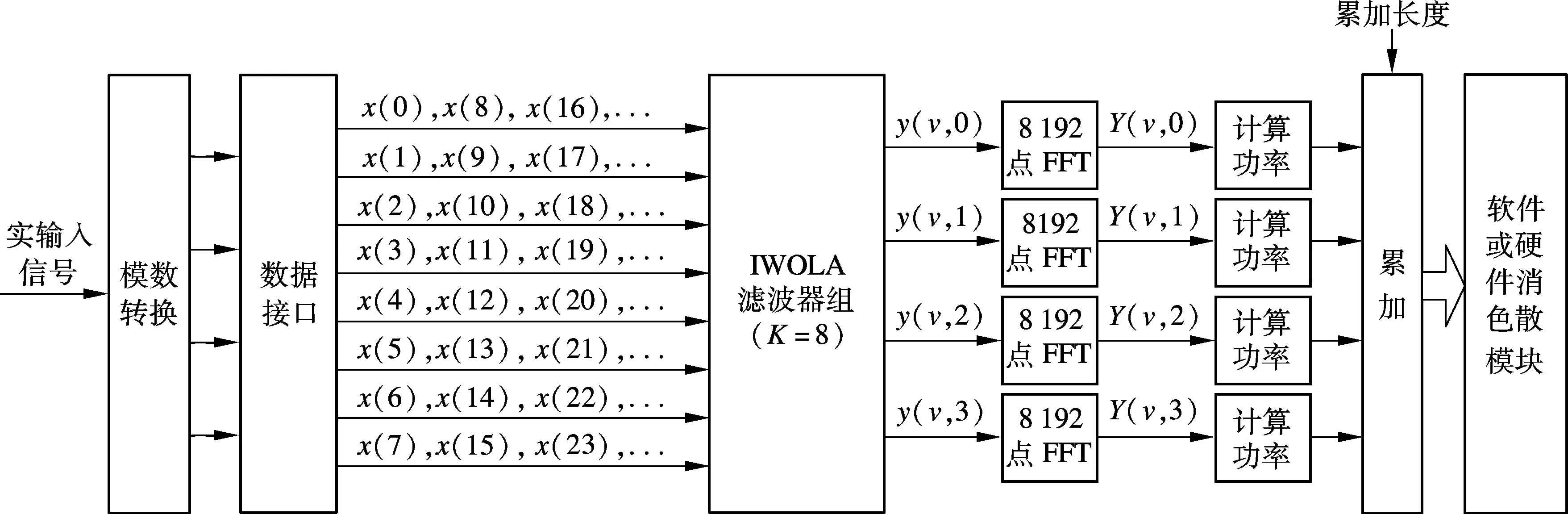
圖4 基于IWOLA的脈沖星消色散數字終端(D=8)

基于IWOLA算法的PFB是在基于WOLA算法的PFB上進行的，將各子帶的中心頻率沿X軸正方向平移π/K個長度,因此,兩者性能相同,由兩者構成的系統的性能也相同.由于系統中PFB的濾波器特性曲線難以達到理想的矩形形狀,因此,PFB輸出的4個通道的過渡邊緣信號會被抑制,但這并不影響脈沖星的消色散處理.另一方面,本文所提的PFB可以方便地向脈沖星信號處理軟件輸出多通道時域數據.

3 片上RAM的利用率分析

在IWOLA算法中,當輸入信號為實信號時,只有K/2組輸出信號需要送入后續處理單元進行處理,節省了一路信號處理需求,尤其是節省了FPGA上的RAM資源,可在復雜的數字系統中產生較大的經濟價值.下面將基于IWOLA算法的脈沖數字終端與基于WOLA算法和基于組合復FFT算法的脈沖星數字終端對FPGA片上RAM資源的利用率進行比較.

3.1 本文終端與基于WOLA算法終端的比較

由式(5)可知,IWOLA算法較WOLA算法增加了2個指數項和1個(-1)l次方項.(-1)l次方項并不會消耗FPGA上的RAM資源.以Xilinx FPGA為例,當數據位寬為16 bit時,2個指數項總共使用了2×16×(K2/D+2K)/(18×1 024)個18 KB RAM和0個DSP資源.此外,當數據位寬為22 bit、相位因子位寬為16 bit、輸出選項為unscaled output時,在Xilinx FPGA上實現一個8 192點FFT將占用57個18 KB RAM和33個DSP資源.不同的數據抽取率和不同通道劃分數下系統對BRAM的節省量見圖5.由圖可知,一方面,資源節省量小于0意味著系統較基于WOLA算法的脈沖星數字終端多占用了BRAM資源,此時應減少PFB的相應通道劃分數;另一方面,系統對BRAM的節省量隨后續處理子單元復雜度的增加而增加,因此,選擇合適的抽取因子和通道數能使系統既滿足設計指標又占用最少的FPGA資源.射電天文終端要求同時處理左右旋2路信號,而增加的2個指數項乘積因子可以被2路處理單元共用,因此,BRAM的資源節省量可能增加1倍,達到13.6%.

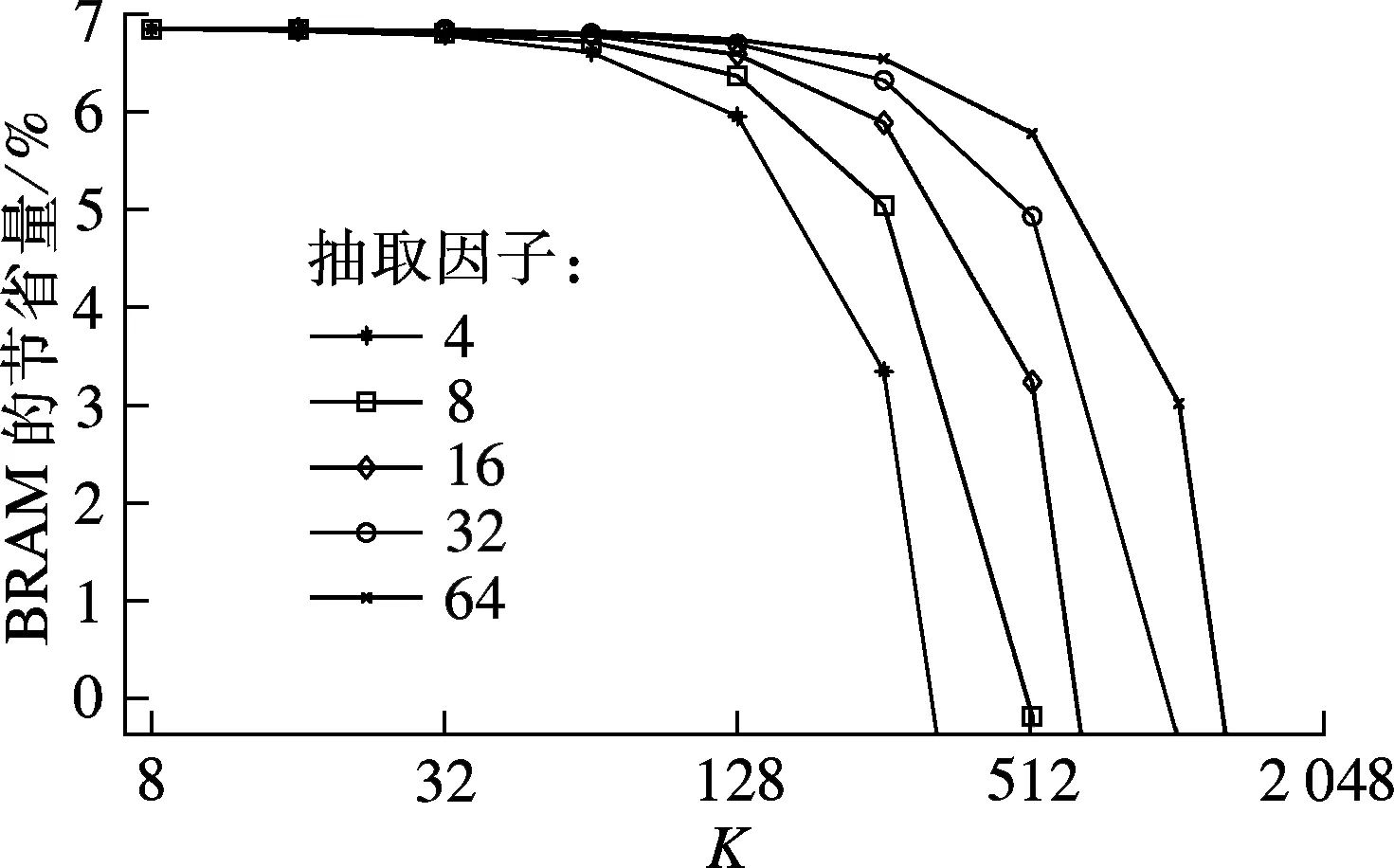
圖5 Xilinx FPGA內BRAM的節省量

3.2 本文終端與基于組合復FFT算法終端的比較

文獻[3]所提出的基于組合復FFT算法的數字終端對FPGA的RAM資源占用較多.為了定量比較該終端與基于IWOLA算法的終端對FPGA資源的節省數量,在Xilinx FPGA上實現了基于IWOLA算法的脈沖星數字終端和文獻[3]中的32 768點組合復FFT算法的脈沖星數字終端.為了增加與基于組合復FFT算法的數字終端的可比性,假定圖4中輸入到8 192點FFT模塊的位寬為8 bit,給出了經ISE綜合后的資源占用對比結果(見表1).由表可知,基于IWOLA算法的脈沖星消色散終端節省了25%的BRAM.

表1 基于IWOLA算法的數字終端與基于組合復FFT的終端資源占用對比

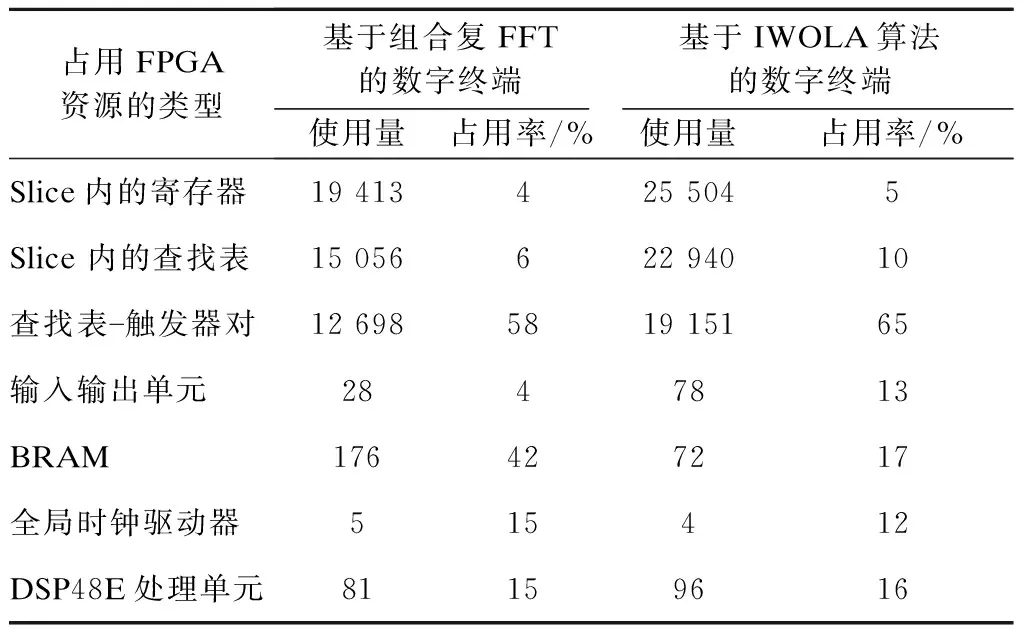
占用FPGA資源的類型基于組合復FFT的數字終端基于IWOLA算法的數字終端使用量占用率/%使用量占用率/%Slice內的寄存器194134255045Slice內的查找表1505662294010查找表觸發器對12698581915165輸入輸出單元2847813BRAM176427217全局時鐘驅動器515412DSP48E處理單元81159616

4 仿真

為了驗證基于IWOLA算法的脈沖星消色散終端的正確性,下面進行功能仿真分析.設K=8;D=8;數據采樣頻率fs=2.4 GHz;輸入信號由3個實正弦信號組成,其頻率分別為400.00, 400.07和1 140.00 MHz.基于IWOLA算法的PFB將帶寬為0～fs/2的寬帶實信號劃分成4個帶寬為300 MHz的復信號,對4路復信號分別進行FFT處理.由第2節可知,這一過程的實質是實信號在經過IWOLA解調后輸出4路復信號,再分別進行8 192點FFT處理,其中第i個通道的中心頻率為ifs/K+fs/(2K).當3個輸入信號經過系統處理后,會有2個輸入信號落在第2個通道內,1個輸入信號落在第4個通道內,第3個通道內沒有有用信號.第2,3,4通道的信號輸出時域和頻域數據見圖6.仿真結果驗證了系統的正確性.

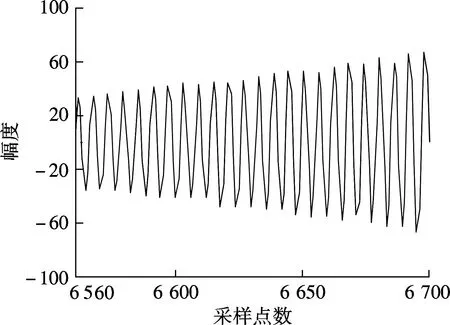
(a) 第2通道信號虛部的時域波形

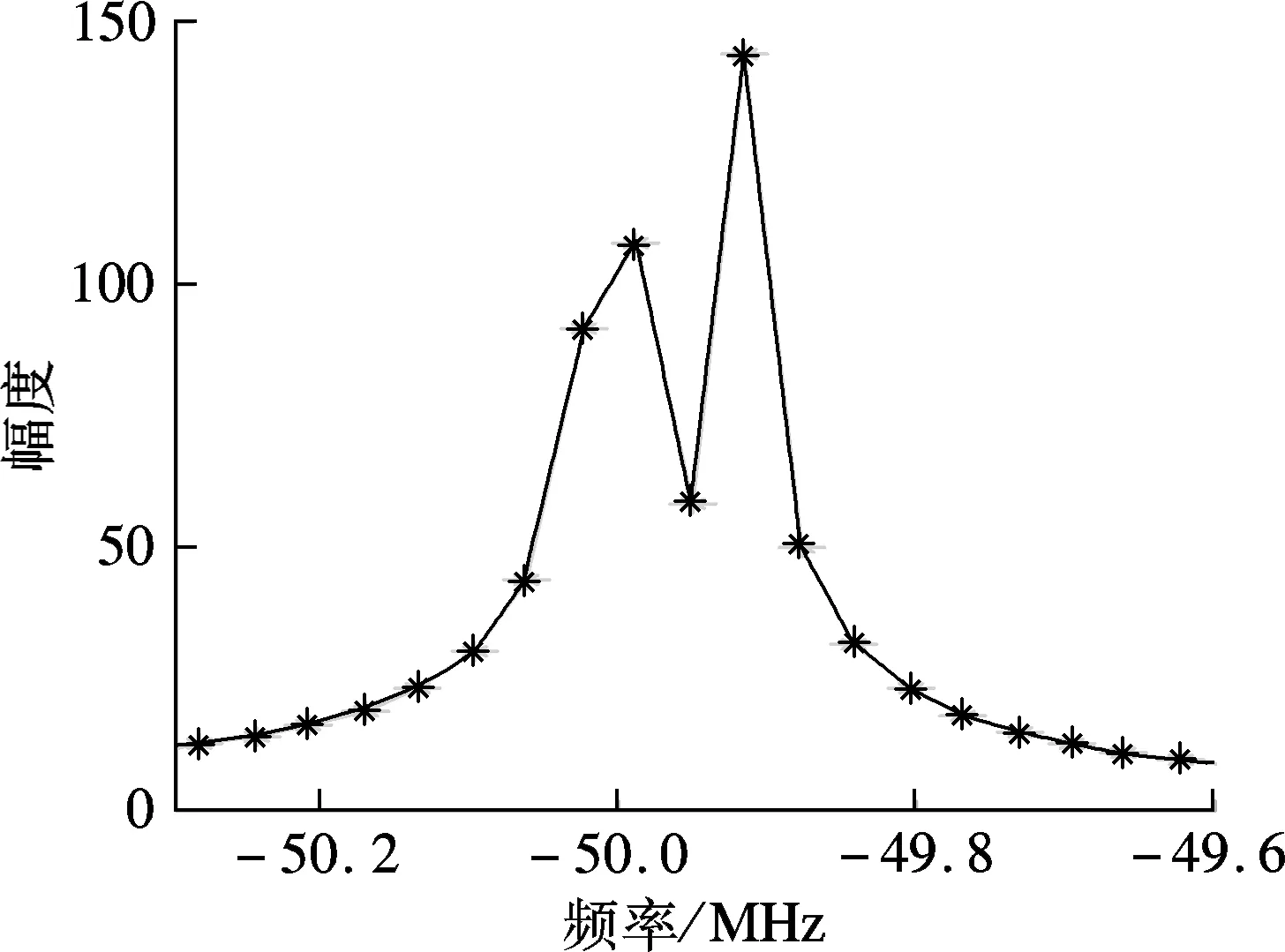
(b) 第2通道的頻域波形

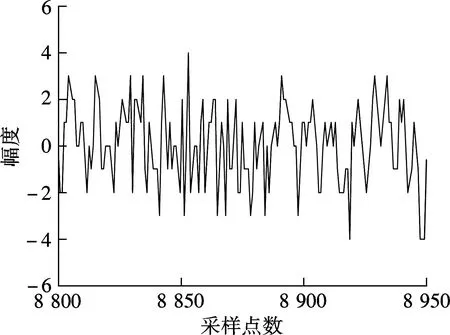
(c) 第3通道信號虛部的時域波形

(d) 第3通道的頻域波形

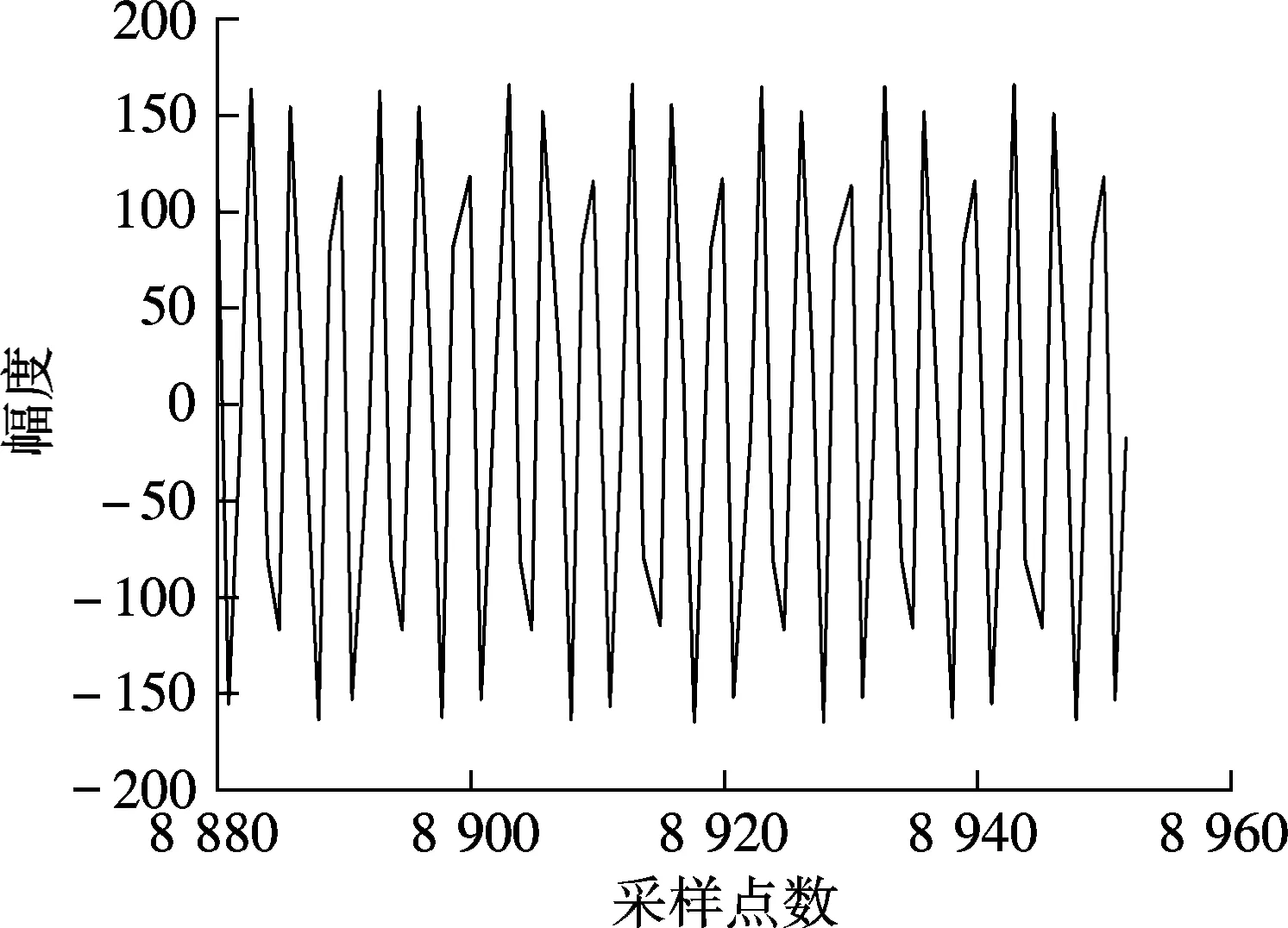
(e) 第4通道信號虛部的時域波形

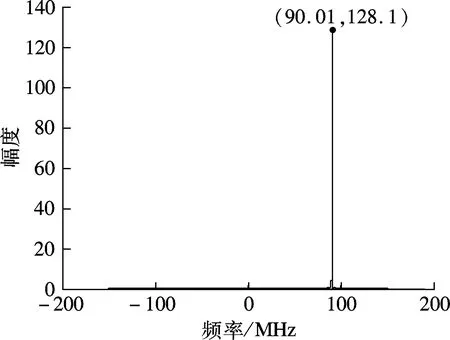
(f) 第4通道的頻域波形

5 結語

本文提出了一種針對寬帶實信號的IWOLA算法,并基于該算法構建了一種脈沖星消色散數字終端.比較了基于IWOLA算法、基于WOLA算法和基于組合復FFT算法的脈沖星消色散數字終端對FPGA片上RAM資源的消耗量.結果表明,在相同條件下,基于IWOLA算法的脈沖星消色散數字終端節省了更多的系統硬件資源,克服了FPGA片上RAM不足引起的設計瓶頸,具有良好的實用價值.最后,對基于IWOLA算法的脈沖星消色散數字終端進行了功能仿真,驗證了其功能的正確性.

References)

[1]Richards B, Nicolici N, Chen H, et al. A 1.5GS/s 4096-point digital spectrum analyzer for space-borne applications [C]//2009IEEECustomIntegratedCircuitsConference. San Jose, CA, USA, 2009: 499-502.

[2]Hochgürtel S, Klein B. Space-efficient FPGA-implementation of FFTs in high-speed applications[C]//5thFPGAWorldConference. Stockholm, Sweden, 2008: 69-72.

[3]Wang X H, Meng Q, Han J L, et al. A wideband real-time spectrometer based on combined complex FFT for radio astronomy[C]//IEEE9thInternationalSymposiumonCommunicationSystems,Networks&DigitalSignalProcess. Manchester, UK, 2014: 691-695.

[4]Wang H, Lu Y X, Wang X G. Channelized receiver with WOLA filterbank[C]//2006InternationalConferenceonRadar. Shanghai, China, 2006: 1-3.

[5]He S S, Torkelson M. A new approach to pipeline FFT processor[C]//The10thInternationalParallelProcessingSymposium. Honolulu, HI, USA, 1996: 766-770.

[6]Parsons A, Backer D, Chen C, et al. A new approach to radio astronomy signal processing: packet switched, FPGA-based, upgradeable, modular hardware and reusable, platform-independent signal processing libraries [EB/OL]. (2005-10)[2014-08-23]. https://casper.berkeley.edu/wiki/Papers.

[7]Brennan R L, Abutalebi R, Sheikhzadeh H. Adaptive filtering using a highly oversampled weighted overlap-add filterbank in an ultra low-power system[C]//TheThirty-SixthAsilomarConferenceonSignals,SystemsandComputers. Pacific Grove, CA, USA, 2002: 806-810.

[8]Liu T, Wang Z G, Wang T, et al. Flexible approach to WOLA-based wideband IF signal analysis[C]//The11thIEEEInternationalConferenceonElectronicMeasurement&Instruments. Harbin, China, 2013: 192-196.

[9]Brennan R, Schneider T. An ultra low-power DSP system with a flexible filter bank [C]//The35thAsilomarConferenceonSignals,SystemsandComputers. Pacifica Grove, CA, USA, 2001: 809-813.

[10]Heller P N, Karp T, Nguyen T Q. A general formulation of modulated filter banks [J].IEEETransactionsonSignalProcessing, 2002, 47(4): 986-1002.

[11]Ravinder K, Khader M A, Rao H N. Implementation of scaled down model of heterogeneous spectrometers for radio astronomy applications using Xilinx FPGAs[J].JournalofEngineeringResearchandApplications, 2013, 3(5): 1596-1599.

[12]Hochgürtel S. Efficient implementations of high-resolution wideband FFT-spectrometers and their application to an APEX galactic center line survey[D]. Bonn, Germany: Mathematisch-Naturwissenschaftlichen Fakult?tder Rheinischen Friedrich-Wilhelms-Universit?t, 2013.

[13]Klein B, Philipp S D, Güsten R, et al. A new generation of spectrometers for radio astronomy: fast Fourier transform spectrometer[C]//2006MillimeterandSubmillimeterDetectorsandInstrumentationforAstronomyⅢ. Orlando, Florida,USA, 2006: 627511-1-627511-12.

[14]楊綠溪.現代數字信號處理[M].北京:科學出版社,2007: 448-454.

[15]Tsakiris N, Hall P, Herfurth S, et al. A 6 GHz digital receiver using COTS prototyping boards [C]//2013InternationalConferenceonRadar. Adelaide, South Australia, 2013: 537-541.

Design of digital backend based on IWOLA for pulsar de-dispersion

Wang Xianhai Meng Qiao Zhang Jianwei Zhang Tianyi

(Institute of RF- & OE-ICs, Southeast University, Nanjing 210096, China)

In a field programmable gate array (FPGA)-based digital backend for pulsar de-dispersion, in order to overcome the bottleneck caused by high-speed on-chip random-access-memory (RAM) resources for system design, a polyphase filter bank (PFB) based on improved weighted overlap-add (IWOLA) algorithm is proposed. Based on this algorithm, a digital backend for pulsar de-dispersion towards wideband real signals is presented. It works with reduced multiband. The theoretical analysis results show that the proposed digital backend saves the system requirements for high-speed on-chip RAM and the subsequent signal processing units, improving the frequency resolution under the premise of guaranteed time resolution. Additionally, it has high computation efficiency and resolves the system design defect caused by polyphase filter discrete Fourier transform (PDFT) algorithm. The digital backend based on the IWOLA algorithm saves the block RAM (BRAM) resources up to 25% when the length of the following FFT in system is 8 192. The simulation results show that the performance of the proposed system meets the requirements of design.

PDFT (polyphase filter discrete Fourier transform); IWOLA (improved weighted overlap-add) algorithm; FPGA (field programmable gate array); de-dispersion

10.3969/j.issn.1001-0505.2015.02.002

2014-10-29. 作者簡介: 王顯海(1980—),男,博士生;孟橋(聯系人),男,博士,教授,博士生導師,mengqiao@seu.edu.cn.

王顯海,孟橋,張健偉，等.一種基于IWOLA的脈沖星消色散數字終端設計[J].東南大學學報:自然科學版,2015,45(2):208-213.

10.3969/j.issn.1001-0505.2015.02.002

P161.4

A

1001-0505(2015)02-0208-06