大地電磁靜態效應模擬研究

時彬，郇恒飛，高鐵，趙院東

1.遼寧省地質礦產調查院，遼寧沈陽 110031；2.中國地質調查局沈陽地質調查中心（沈陽地質礦產研究所），遼寧沈陽 110034

大地電磁靜態效應模擬研究

時彬1，郇恒飛2，高鐵2，趙院東2

1.遼寧省地質礦產調查院，遼寧沈陽 110031；2.中國地質調查局沈陽地質調查中心（沈陽地質礦產研究所），遼寧沈陽 110034

通過數值模擬分析模型寬度、厚度、埋深、電阻率等參數對視電阻率、視相位的影響，發現TM模式受靜態效應影響嚴重；異常體產生的靜態效應畸變隨埋深變淺而增大，地表異常造成的畸變尤為嚴重；異常體與圍巖的電阻率差異越大造成的靜態效應越明顯；相比厚度，同比改變異常體的寬度對視電阻率的影響更大.通過曲線擬合各參數與視電阻率的相關函數，估算參數計算異常體對視電阻率的影響程度，以達到改正的目的.

大地電磁；靜態效應；數值模擬；對數相對誤差

在大地電磁測量中，常遇到因地表異常或地形而產生靜態效應［1］.正確認識靜態效應，分析靜態效應影響因素，定量地認識靜態效應的影響量有利于更好地處理、解釋大地電磁資料.筆者通過數值模擬分析靜態效應影響因素，并從異常體的寬度、厚度、埋深、電阻率等方面進行模擬討論，并以擬合曲線函數定量地總結各影響因素對靜態效應的影響程度，以此作為地表地形、異常體產生靜態效應的改正依據.

1 數值模擬

大地電磁數值模擬采用二維有限元數值模擬計算，每個剖分單元采用雙線性差值進行差值求解［2-3］.

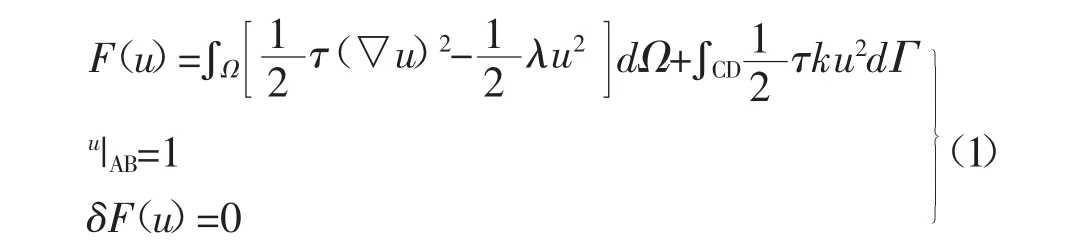
其中，u為Ex或Hx，Ω為二維求解區域.

TE模式中，上邊界AB處離地面足夠遠，u為Ex，τ=1/（iωμ），λ=σ-iωε；

TM模式中，上邊界AB在地面，u為Hx，τ=1/σ，λ= iωμ.

其中，ω為較頻率，u為介質磁導率，σ為介質電導率，ε為介電常數，CD為下邊界.

2 數值模擬程序驗證

建立三層模型，模型結構見圖1.數值模擬正演TE、TM模式視電阻率、視相位結果與解析解結果對比見圖2、3.

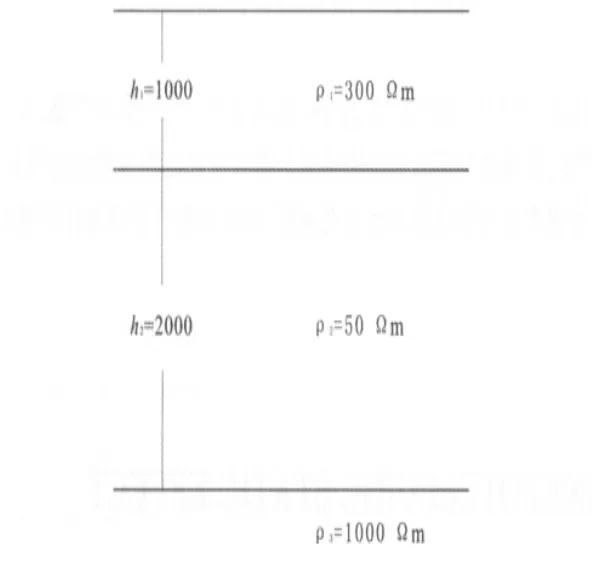
圖1 三層模型示意圖Fig.1 Three-tier model diagram

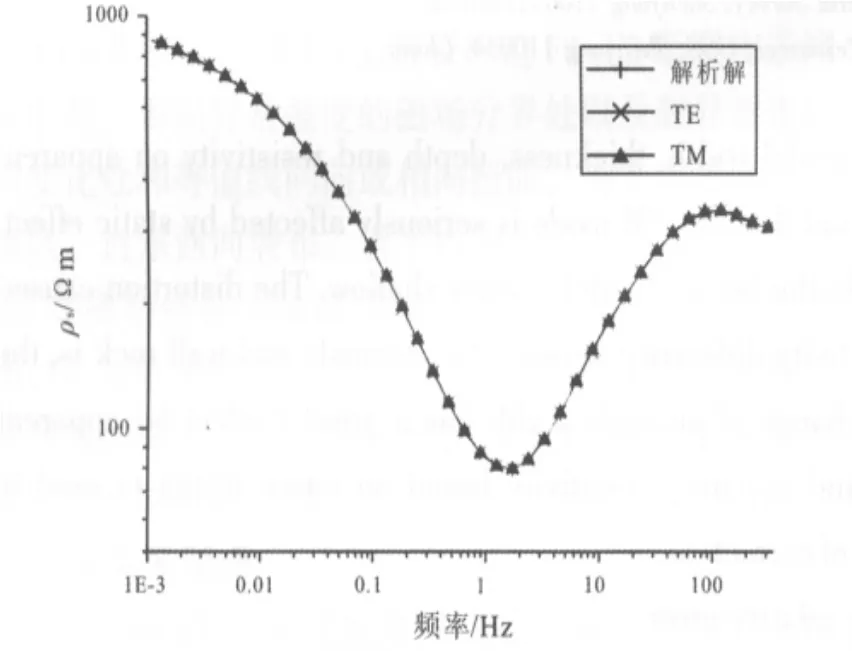
圖2 視電阻率曲線對比Fig.2 Comparison of apparent resistivity curres

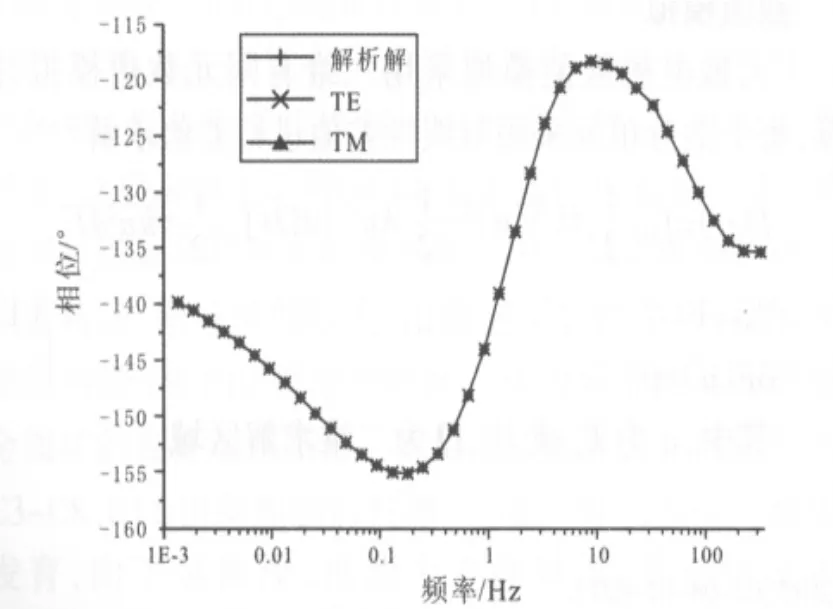
圖3 視相位曲線對比Fig.3 Comparison of apparent phase curves

兩種模式視電阻率、視相位曲線一致性較好.通過結果計算得到，TE模式視電阻率誤差為0.34%，TM模式誤差為0.14%；TE模式視相位誤差為0.16%，TM模式視相位誤差為0.15%.證明程序計算正確精度較高.

3 靜態效應數值模擬

建立三層模型如圖1，在背景場基礎上設定二維異常體規模為100 m×50 m，異常體位于地表，低阻異常體電阻率為10 Ωm，高阻異常體電阻率為30 000 Ωm.在地表異常體中心，得到TE、TM模式下的視電阻率、視相位曲線見圖4～7.解析解為不存在異常體時的背景視電阻率、視相位曲線.

3.1 不同模式、不同性質異常體靜態效應對比

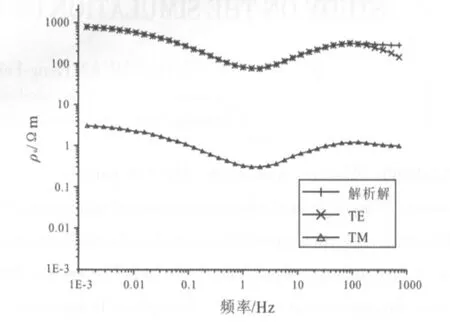
圖4 地表低阻異常視電阻率曲線對比Fig.4 Comparison of apparent resistivity curves of surface low resistance anomaly

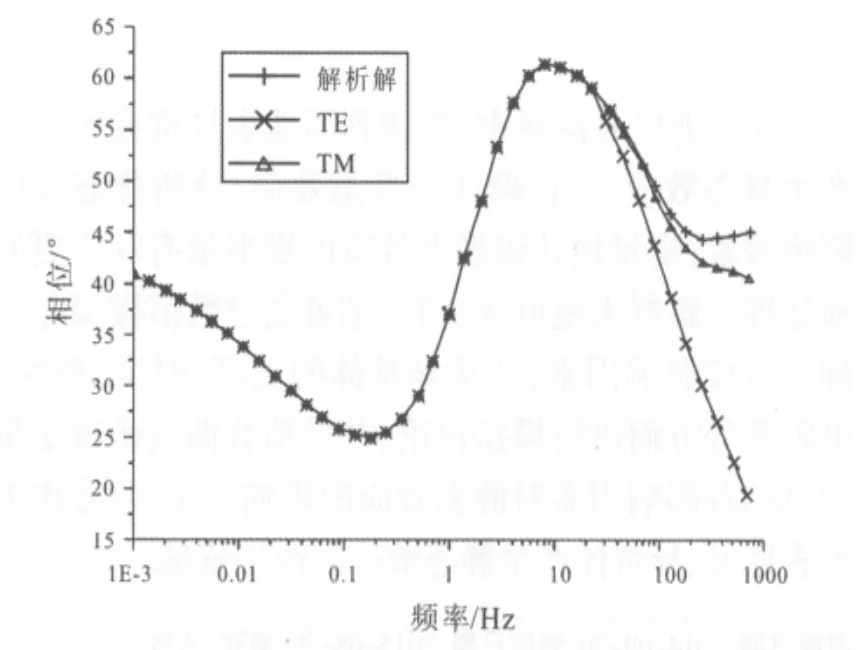
圖5 地表低阻異常視相位曲線對比Fig.5 Comparison of apparent phase curves of surface low resistance anomaly

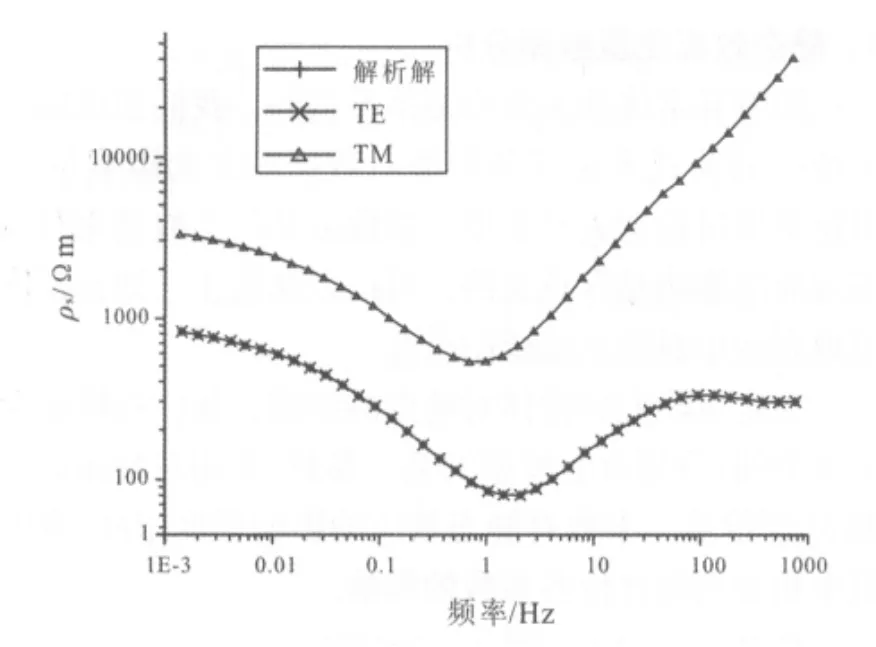
圖6 地表高阻異常視電阻率曲線對比Fig.6 Comparison of apparent resistivity curves of surface high resistance anomaly

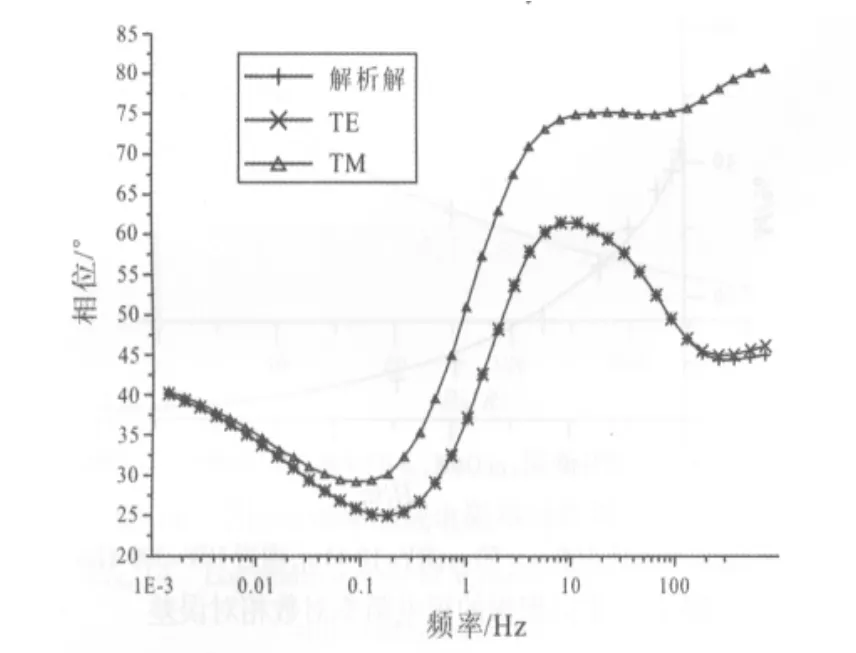
圖7 地表高阻異常視相位曲線對比Fig.7 Comparison of apparent phase curves of surface high resistance anomaly

由圖4～7可以看出，當地表存在異常體，TE模式視電阻率、視相位曲線與無異常體狀態下的曲線基本一致，無明顯數據畸變［4］；無論異常體為高阻還是低阻，TM模式視電阻率曲線出現嚴重的數據畸變，這個畸變可達幾個數量級.TE模式對地表異常分辨率不高，受靜態效應影響較小；而TM模式對水平方向電阻率分辨率較高，視相位也無明顯畸變.在實際勘測中，TM模式更容易受到靜態效應影響，而地表的低阻異常體引起的靜態效應更為常見.下面主要分析TM模式下不同參數對視電阻率曲線的影響.

3.2 模型深度變化對靜態效應的影響

背景三層模型和低阻異常體模型不變，只改變異常體頂端埋深H，得到視電阻率曲線如圖8.

異常體埋深對視電阻率曲線影響很大，隨著異常體埋深由深到淺，其靜態效應逐漸增強，視電阻率曲線存在較大數值的平移；異常體埋深變化只會造成視電阻率曲線平移，基本不會改變形態；當異常體出露地表時，其造成的數據畸變程度會突然增大，這種畸變是數值計算造成的.

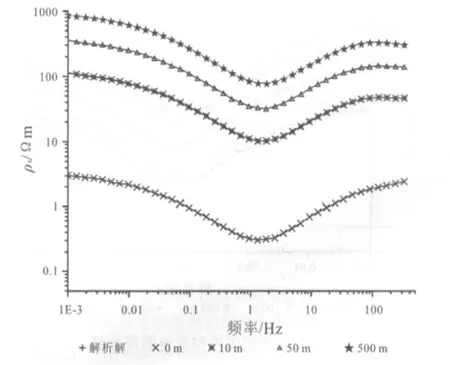
圖8 不同深度異常體對視電阻率曲線影響Fig.8 Effect of anomalies with different depth on apparent resistivity

3.3 模型電阻率變化對靜態效應的影響

為討論異常體電阻率對靜態效應的影響，將模型置于埋深100 m處，模型其他參數不變，改變模型電阻率，其視電阻率曲線對比見圖9.

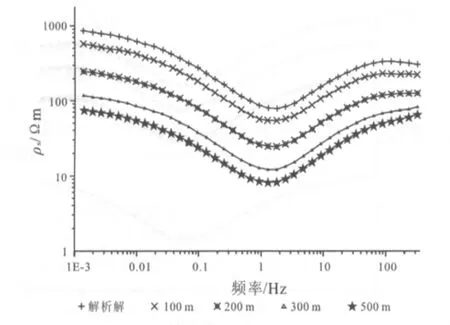
圖9 不同電阻率異常體對視電阻率曲線影響Fig.9 Effect of anomalies with different resistivity on apparent resistivity

靜態效應畸變程度與其異常體的相對電阻率差異RW/RY有關（RW為圍巖電阻率，RY為異常體電阻率），相對電阻率差異越大，靜態效應越明顯，大的相對電阻率差異造成的數據畸變可達幾個數量級.各頻率對異常體反映程度基本相同.

3.4 模型寬度、厚度、大小對靜態效應的影響

將模型置于埋深100 m處，模型其他參數不變，分別改變模型的寬度L、厚度d，等比增大模型規模，各參數影響的視電阻率曲線對比見圖10～12.

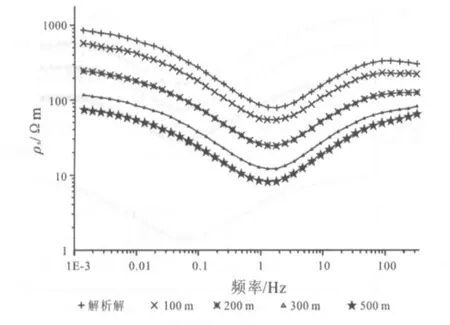
圖10 不同寬度模型視電阻率曲線Fig.10 Apparent resistivity curves of models with different width

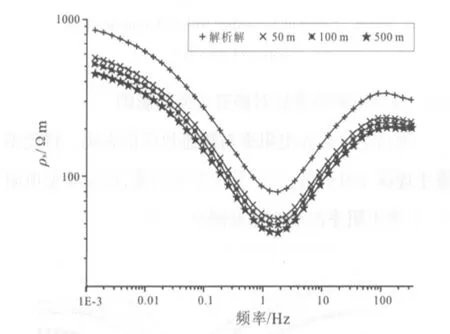
圖11 不同厚度模型視電阻率曲線Fig.11 Apparent resistivity curves of models with different thickness

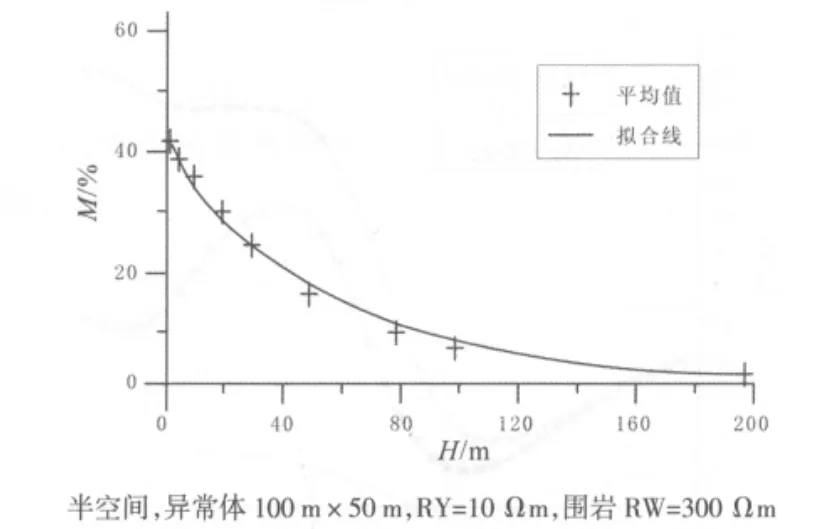
圖12 不同大小模型視電阻率曲線Fig.12 Apparent resistivity curves of models with different size

從二維大地電磁模擬計算結果可以看出，異常體的寬度L和厚度d對視電阻率均有影響，寬度和厚度的增大均會造成靜態效應畸變增強，但異常體的寬度d對TM模式視電阻率影響更大.在同比改變異常體規模時，模擬計算得到的視電阻率曲線形態發生變化.

4 靜態效應定量數據分析

影響異常體靜態效應是多參數的，我們很難用一個統一的公式來定義各參數對數據畸變的影響量［5］.但定量地討論地表異常單一參數或某些參數變化對靜態效應的影響是有意義的，可以以此改正已知異常體或地表地形對數據造成的畸變.

為定量研究異常體對畸變的影響，我們將模型置于半空間，分別改變模型的某一參數，采用對數相對誤差M評價單一參數對靜態效應的影響程度，并以視電阻率相對誤差評價各參數的影響.

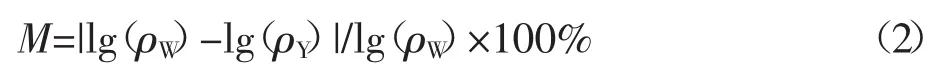
其中，ρY為存在靜態效應時的視電阻率，ρW為無靜態效應時的背景視電阻率.

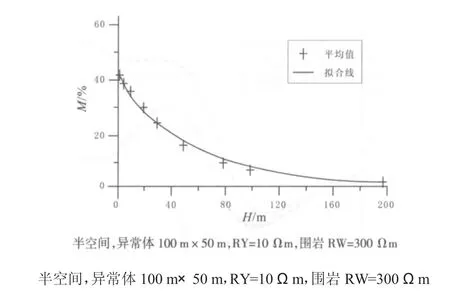
圖13 不同埋深的視電阻率對數相對誤差Fig.13 Log relative error of apparent resistivity with different depth

4.1 異常體埋深對靜態效應的影響

從前文的分析可以看出，同一異常體位于地下不同深度，對靜態效應的影響程度差異很大.從圖13可以看出，不同埋深異常體視電阻率對數相對誤差偏差較小，證明引起靜態效應的異常體在不同頻率引起畸變的程度幾乎相同.當異常體位于地表時，電阻率畸變陡增，且各頻點影響程度有所不同；異常體位于地下，異常體不會改變視電阻率曲線形態，其對數相對誤差可用擬合函數表示.在其他因素不考慮的前提下，異常體頂端埋深H引起靜態效應畸變程度可用近似函數表示：

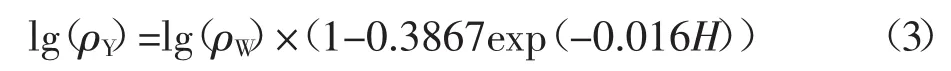
其中，ρY為存在靜態效應時的視電阻率，ρW為無靜態效應時的電阻率，H為異常體頂端埋深.

4.2 異常體相對電阻率對靜態效應的影響

忽略其他相關因素，我們只考慮異常體電阻率對靜電效應的影響.異常體產生的靜態效應強弱與相對視電阻率的大小有關，異常體與圍巖電阻率差值越大，其靜態效應越強.當異常體其他因素不變，不同電阻率的異常體引起靜態效應強度的相關關系見圖14，可用函數（4）表示：

其中，ρY為存在靜態效應時的視電阻率，ρW為無靜態效應時的視電阻率，RW為圍巖電阻率，RY為異常體電阻率.

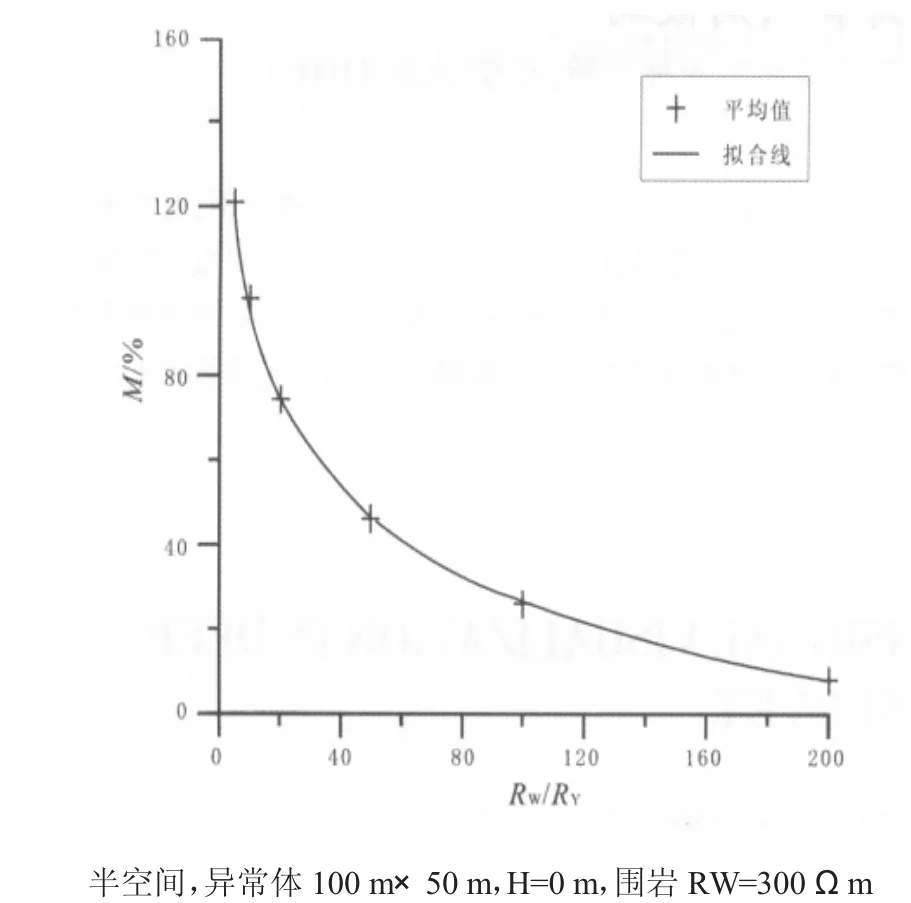
圖14 不同電阻率的視電阻率對數相對誤差Fig.14 Log relative error of apparent resistivity with different resistivity

4.3 異常體規模對靜態效應的影響

改變異常體的邊長s，視電阻率對數相對誤差變化規律見圖15.無論異常體多大規模，靜態效應都會存在，而且會影響各個頻點；靜態效應隨s增大而增強.異常體規模對靜態效應的影響不是遞增的，當地質體增大到一定規模，對靜態效應的數據畸變逐漸減弱，視電阻率值就會趨向于表現為他的真電阻率，在此不作討論.

當異常體其他因素不變，不同電阻率的異常體引起靜態效應強度可用函數（5）表示：

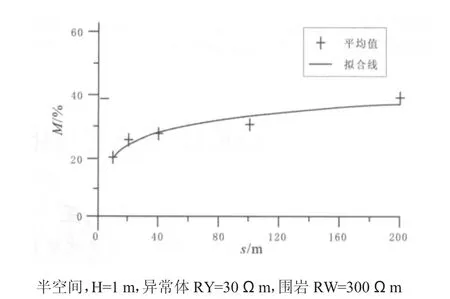
圖15 不同異常體規模的視電阻率對數相對誤差Fig.15 Log relative error of apparent resistivity with different anomaly size

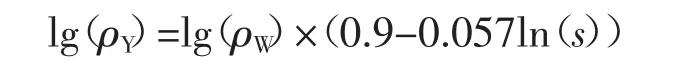
對于已知地表異常和地形引起的數據畸變，可用上述公式進行改正靜態效應畸變.

5 結論

1）TE模式視電阻率和相位受到因異常體產生的靜態效應影響較小；TM模式視電阻率受到高阻、低阻異常體靜態效應影響較大.

2）異常體的埋深、與圍巖的電阻率差值對靜態效應影響較大，會造成視電阻率值數量級上的畸變.

3）通過數據分析擬合得到的函數可以定量地分析各參數對靜態效應產生的影響，可以用于地表等已知異常體產生的靜態效應校正.

［1］陳樂壽，王光鍔.大地電磁測深法［M］.北京：地質出版社,1990.

［2］曾國.大地電磁二維有限元正演數值模擬［D］.長沙：中南大學,2008.

［3］朱威.二維大地電磁正反演人機交互解釋系統研究［D］.長春：吉林大學,2009.

［4］陳輝，王春慶，雷達，等.CSAMT法靜態效應模擬及其校正方法對比［J］.物探化探計算技術,2007,29（S1）:64—67.

［5］羅延鐘，何展翔，馬瑞伍，等.可控源音頻大地電磁法的靜態效應校正［J］.物探與化探,1991,15（3）:196—202.

STUDY ON THE SIMULATION OF MAGNETOTELLURIC STATIC EFFECT

SHI Bin1,HUAN Heng-Fei2,GAO Tie2,ZHAO Yuan-dong2

1.Liaoning Institute of Geological and Mineral Survey,Shenyang 110031,China; 2.Shenyang Institute of Geology and Mineral Resources,CGS,Shenyang 110034,China

With analysis on the effect of parameters such as model width,thickness,depth and resistivity on apparent resistivity and apparent phase by numerical simulation,it is found that the TM mode is seriously affected by static effect. The static distortion caused by anomalous bodies increases while the burial depth becomes shallow.The distortion caused by surface anomaly is particularly serious.The greater the resistivity difference between the anomaly and wall rock is,the more obvious its static effect is.Compared to thickness,the change of anomaly width has a greater effect on apparent resistivity.The correlation function between the parameters and apparent resistivity based on curve fitting is used to estimate the influence of anomalies on resistivity for the purpose of correction.

MT;static effect;numerical simulation;logarithmic relative error

1671-1947（2015）04-0373-05

P631.3

A

2014－09－20；

2015-08-29.編輯：張哲．

中國地質調查局項目“黑龍江多寶山白石砬子地區礦產地質調查”（［2015］02-08-01-021）.

時彬（1986—），男，碩士，從事地球物理勘查工作，通信地址遼寧省沈陽市皇姑區寧山中路42號羽豐大廈.

高鐵（1983—），男，博士，工程師，從事重磁電理論及應用研究，通信地址遼寧省沈陽市皇姑區黃河北大街280號，E-mail//39085496@qq.com