非正交軸系激光經緯儀測量技術研究

吳 斌，楊 松

(天津大學精密測試技術及儀器國家重點實驗室，天津300072)

引 言

隨著航空(大型客機及運輸機等)、航天(火箭、衛星、飛船及空間站等)、電力(大型火電、水電及核電機組等)、軌道交通(高鐵、地鐵及城市軌道車輛等)、汽車、船舶(航空母艦、大型客輪、油輪等)、工程機械(隧道挖掘和盾構機、浮式起重機等)、重型機械(800MN大型模鍛壓機等)以及大型通訊設備(探月工程50m，66m口徑地面天線等)等國家重大技術裝備制造業水平的提高，在大尺寸范圍內對單點坐標、幾何尺寸及曲面特征等的現場、快速、精密測量已成為工業測量的研究熱點和難點。目前，激光跟蹤儀、全站儀、經緯儀和攝影測量相關設備是實現大空間、大尺寸對象精密制造、裝調的主要測量手段。激光跟蹤儀和全站儀測量時需要合作目標(靶鏡)，攝影測量設備往往需要人工粘貼標記，都無法實現測量自動化，而新型激光電子經緯儀(Leica TM5100A/TM6100A)由于具備伺服驅動和激光瞄準等功能，為實現自動化測量提供了新的途徑［1］。

為滿足船舶分段的自動化測量需要，作者［2］曾研究了以兩臺Leica TM5100A激光電子伺服經緯儀為基礎測量平臺，結合與視準軸同軸投射的準直激光技術和視覺跟蹤引導技術，構建了一套面向大空間、大尺寸對象現場自動測量的系統樣機。該系統在傳統經緯儀測量方法的基礎上引入了視覺測量的原理機制，利用多分辨率視覺成像方法對被測區域進行掃描監測，對被測目標進行自動識別、匹配和跟蹤瞄準，通過計算被測點成像位置信息控制伺服馬達驅動的高精度電子經緯儀進行被測點的空間方位角度測量，再由多臺經緯儀交會實現大空間范圍內點坐標的測量。但在后續研究和應用的過程中發現，高精度電子經緯儀對制造工藝要求嚴格、造價昂貴，制約了其應用推廣。

系統成本主要來自于經緯儀。對于傳統經緯儀而言，三軸正交(即垂直軸與水平軸正交，水平軸與視準軸正交，且三軸交于一點)是實現精確角度測量對儀器本身的結構要求，若不能滿足，則會產生水平軸傾斜誤差、垂直軸傾斜誤差及視準軸誤差，從而影響角度測量的準確性［3］。雖然上述誤差可以進行補償，但補償范圍有限。因此，為滿足三軸正交的結構要求，在儀器的設計、加工、裝配、檢校和維護等方面有嚴格的要求，從而決定了該儀器制造和維護的高成本。

作者擬借鑒經緯儀的三軸結構模式，但突破傳統經緯儀三軸正交的結構要求，提出并研究一種新的非正交軸系激光經緯儀架構及其測量原理與方法［4-5］。為大空間、大尺寸對象精密、自動測量提供新的理論支持和更為合理、有效的技術手段與裝置。

1 非正交軸系激光經緯儀的架構

從組成部件來看，與傳統經緯儀相比，非正交軸系激光經緯儀有類似的水平度盤和豎直度盤，不同之處是采用準直激光器代替了傳統的望遠鏡。相應地，也存在3個軸:水平度盤旋轉中心軸線、豎直度盤旋轉中心軸線及準直激光束。借鑒傳統經緯儀的三軸概念，將其三軸也分別稱為:豎直軸、橫軸和視準軸，但豎直軸與橫軸、橫軸與視準軸均無正交要求，且三軸也無需交于一點，因此稱之為非正交軸系。由于豎直軸僅表示水平度盤的旋轉中心軸線，不要求與大地的垂直關系，因此非正交軸系激光經緯儀在使用時無需整平。視準軸由一準直激光束標識，將傳統不可見的望遠鏡光軸進行了可視化，多臺儀器測量時，在被測特征處激光光斑的重合則標志著視準軸的空間交會。同樣，參照傳統經緯儀中的相關概念，將非正交軸系激光經緯儀圍繞豎直軸旋轉時，水平度盤提供的角度稱為水平角，圍繞橫軸旋轉時，豎直度盤提供的角度稱為豎直角。但此水平角和豎直角，與傳統正交軸系經緯儀的水平角和豎直角意義完全不同。傳統經緯儀與非正交軸系激光經緯儀架構如圖1所示。圖中，1為豎直軸，2為安放平臺，3為水平度盤，4為橫軸，5為豎直度盤，6為視準軸。

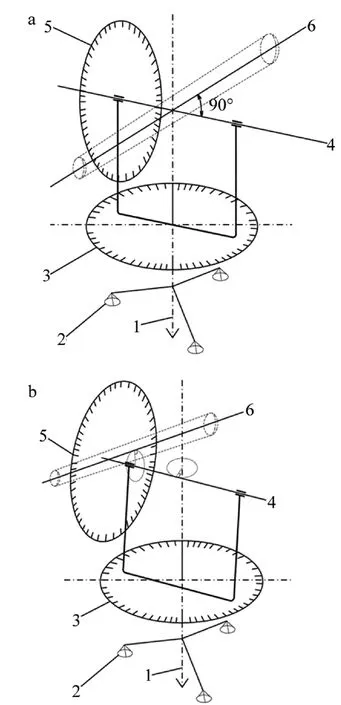
Fig.1 a—architecture of traditional theodolites b—architecture of non-orthogonal shafting laser theodolites

上述非正交軸系架構中，豎直軸、橫軸和視準軸三軸無正交結構要求，也無需交于空間一點，因此，大大降低了對軸系設計、加工、裝配和維護等方面的要求，降低了儀器制造成本。甚至由1維轉臺即可組裝精密的經緯儀，極大地拓展經緯儀的應用領域，同時也發展了一種新的測量方法與技術。

2 測量原理和數學模型

2.1 測量原理

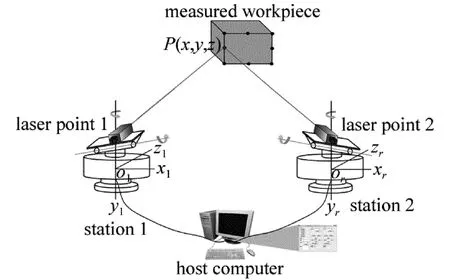
Fig.2 Schematic diagram of measurement system of non-orthogonal shafting laser theodolites

非正交軸系激光經緯儀的水平角和豎直角雖然與傳統正交軸系經緯儀的水平角和豎直角意義不同，但由水平角和豎直角同樣確定了非正交軸系激光經緯儀的視準軸的空間方位，因此，基于兩臺或以上非正交軸系激光經緯儀的視準軸空間交會［6］也可實現空間坐標的測量。如圖2所示，準直激光光束即為可視化的視準軸，兩激光束在被測點處所形成光斑的重合即表示視準軸的空間交會。

2.2 非正交軸系激光經緯儀數學模型

根據圖1所示的非正交軸系激光經緯儀架構及2維云臺運動軌跡［7］，以測站1為例，建立如圖3所示的非正交軸系激光經緯儀坐標系o1-x1-y1-z1。首先選取豎直軸上任意一點為坐標原點o1，定義豎直軸向下方向為y1軸，過o1點做o1y1的垂線并定義為o1x1，則o1z1軸滿足右手法則。由于豎直軸即為y軸，故不存在傳統意義上的豎直軸傾斜誤差。

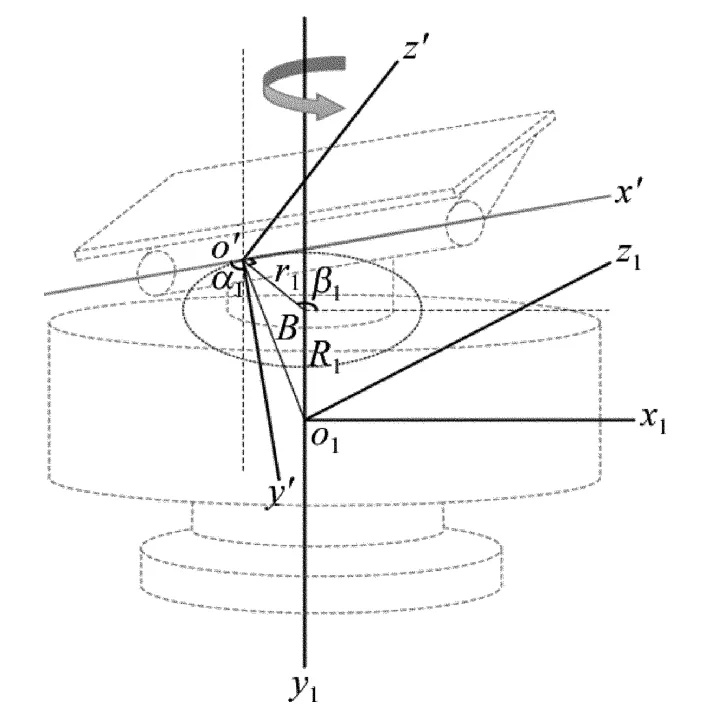
Fig.3 Sketch of coordinate system(o1-x1-y1-z1)

如圖3所示，若用o'x'表示橫軸，其中o'為橫軸與豎直軸兩異面直線的公垂線與橫軸的交點，公垂線與豎直軸的交點用B表示。選取過o'點與o'x'軸垂直的任意直線為o'y'軸，滿足右手法則建立豎直度盤的坐標系o'-x'-y'-z'。假設o'x'與o1y1軸的夾角為α1，公垂線的距離，o'B與o1x1軸的夾角為β1。根據幾何關系，可以得到:

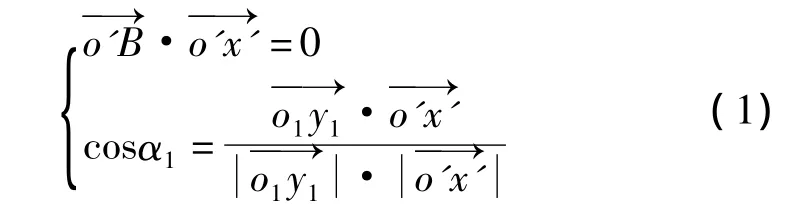
測量時，橫軸o'x'以B點為中心圍繞豎直軸o1y1旋轉。如果得到固定距離r1和R1，固定角度α1和動態角度β1，便可以通過(1)式得到橫軸o'x'在坐標系o1-x1-y1-z1中的實時方程。得出橫軸的直線方程后，則可以通過上述方法建立動態測量坐標系o'-x'-y'-z'，如圖4所示。其中o'-x'-y'-z'可由o1-x1-y1-z1旋轉平移得到。

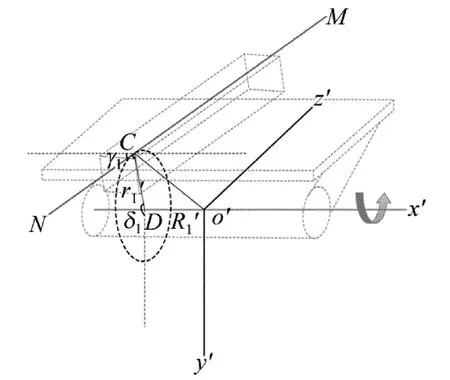
Fig.4 Sketch of dynamic coordinate system(o'-x'-y'-z')

如圖4所示，用MN表示視準軸，C為視準軸與橫軸兩異面直線的公垂線與視準軸的交點，公垂線與橫軸的交點用D表示。假設MN與o'x'軸的夾角為γ1，公垂線的距離，CD與o'y'軸的夾角為δ1。根據幾何關系，可以得到:

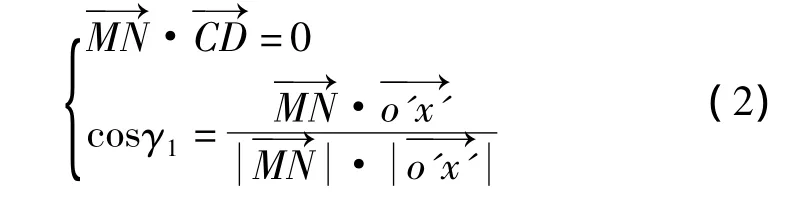
測量時，視準軸MN以D點為中心圍繞橫軸o'x'旋轉。如果得到固定距離r1'和R1'，固定角度γ1和動態角度δ1，便可以通過(2)式得到視準軸MN在動態坐標系o'-x'-y'-z'中的實時方程。根據橫軸的實時方程，可以得到由o1-x1-y1-z1到o'-x'-y'-z'的矩陣Mr。最終，可以得到視準軸MN在坐標系o1-x1-y1-z1中的實時方程。坐標系o1-x1-y1-z1與o'-x'-y'-z'的關系如下所示:

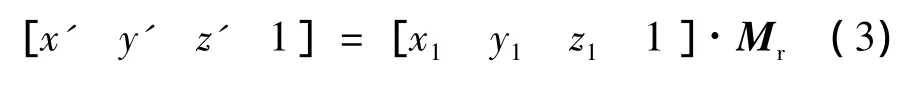
其中，

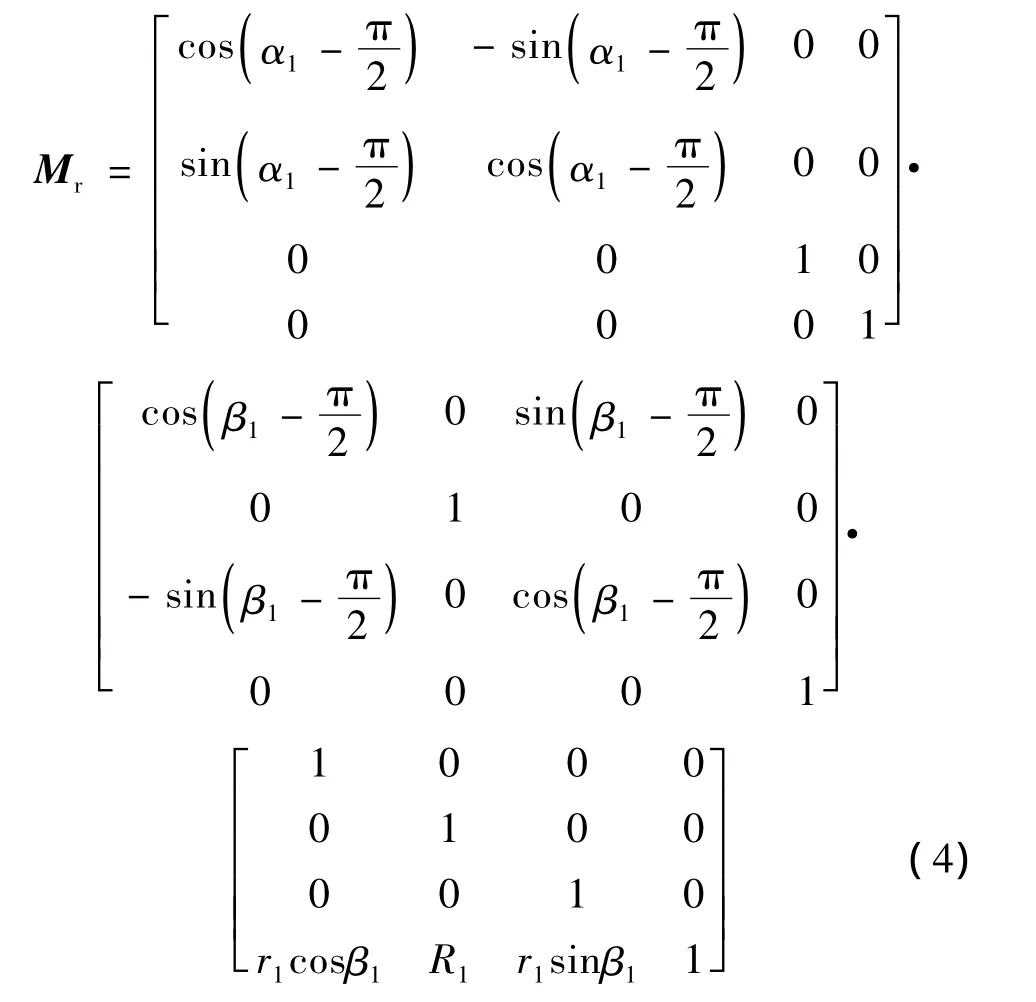
2.3 測量系統數學模型

由前述內容可知，采用兩臺或多臺非正交軸系激光經緯儀，基于其視準軸的空間交會可以實現空間點的坐標測量。在得到了非正交軸系激光經緯儀的視準軸動態方程的基礎上，若能夠建立起非正交軸系激光經緯儀坐標系之間的關系，則可將其視準軸的動態方程統一到一個坐標系下，從而聯立求解出交會空間點的坐標。如圖5所示，在借鑒視覺測量技術中的雙目測量模型的基礎上［8］，建立了非正交軸系激光經緯儀的測量系統模型。測站1中，o1'為視準軸o1'P與z1=0平面的交點，建立動態測量坐標系o1'-x1'-y1'-z1'，圖像坐標系為O1-X1-Y1，焦距為1mm;測站2中，or'為視準軸or'P與zr=0平面的交點，建立動態測量坐標系or'-xr'-yr'-zr'，圖像坐標系為Or-Xr-Yr，焦距為1mm。

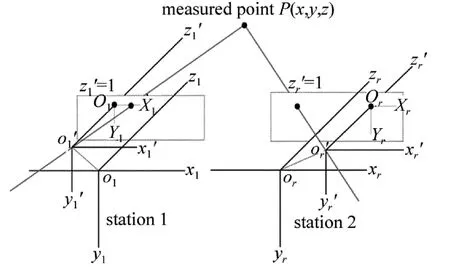
Fig.5 Measurement system model of non-orthogonal shafting laser theodolites

由攝像機透視變換模型［9-10］可以得到:

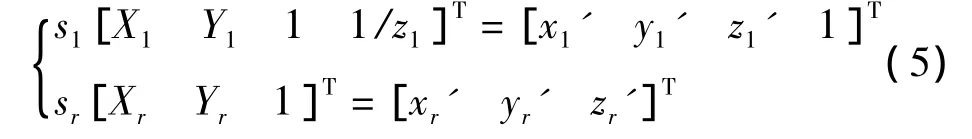
式中，s1代表圖像坐標系O1-X1-Y1與動態坐標系o1'-x1'-y1'-z1'的比例關系，sr代表圖像坐標系Or-Xr-Yr與動態坐標系or'-xr'-yr'-zr'的比例關系。

測站1中動態測量坐標系o1'-x1'-y1'-z1'可由坐標系o1-x1-y1-z1平移得到，它們的關系如下式所示:

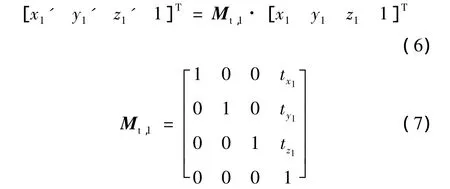
測站2中動態測量坐標系or'-xr'-yr'-zr'可由坐標系or-xr-yr-zr平移得到，它們的關系如下式所示:

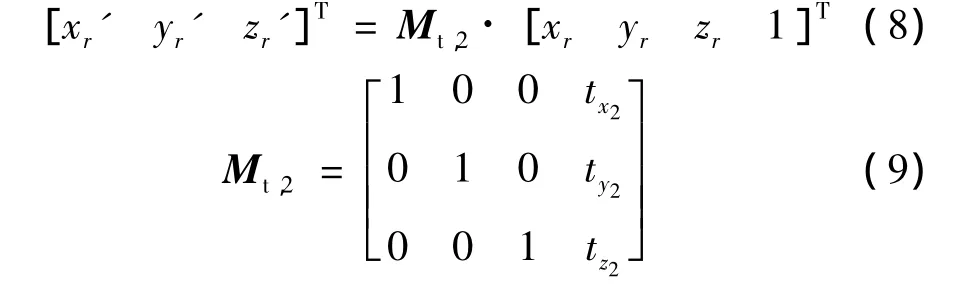
在非正交軸系激光經緯儀測量系統模型中，坐標系o1-x1-y1-z1與坐標系or-xr-yr-zr的位置關系固定不變。它們的關系如下式所示:

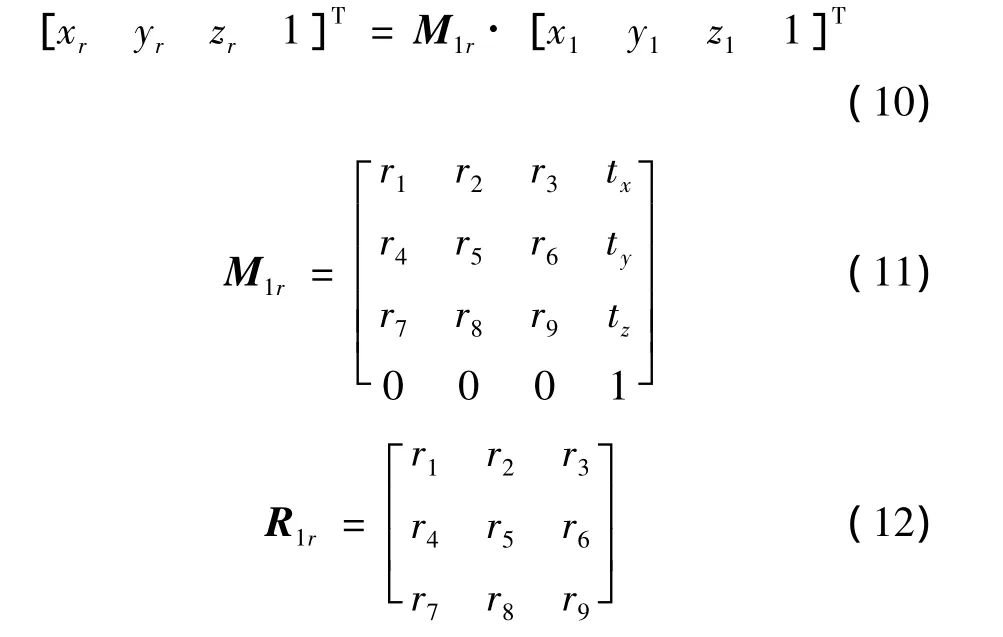
式中，M1r為測站1與測站r之間的矩陣，M1r矩陣分為旋轉矩陣和平移矩陣，R1r為其中的旋轉矩陣。

聯系(5)式～(12)式，可以得到測站1中圖像坐標系O1-X1-Y1與測站2中圖像坐標系Or-Xr-Yr的轉換關系，如下式所示:

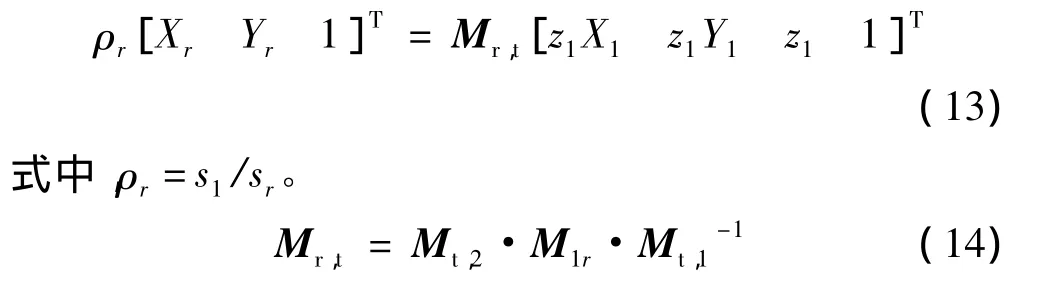
于是，在坐標系o1-x1-y1-z1中空間3維點坐標可以表示為:

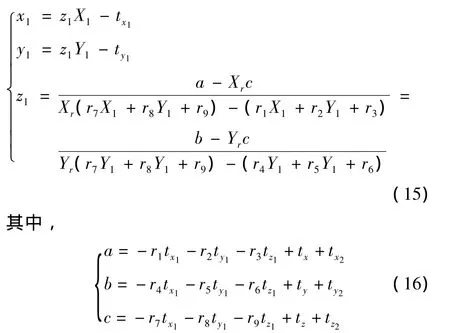
根據非正交軸系激光經緯儀測量系統模型，已知空間點在測站1、2中的圖像坐標［11-12］，只要求出M1r中的旋轉和平移因子，可以被測點在坐標系o1-x1-y1-z1中的空間坐標。由(15)式得到:

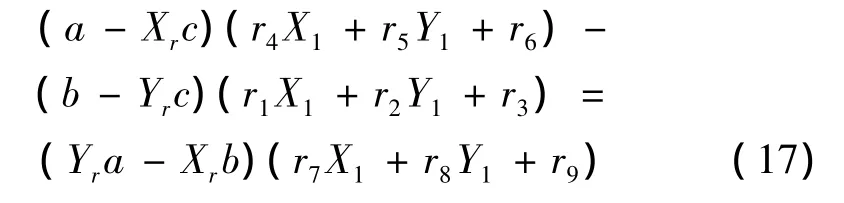
(17)式是一個含有12個參量的非線性方程，用函數f(x)=0 來表示，其中參量 x=(tx，ty，tz，r1，r2，r3，r4，r5，r6，r7，r8，r9)。由于旋轉矩陣 R1r是正交的，具有6個正交約束條件。由此構成如下罰函數:

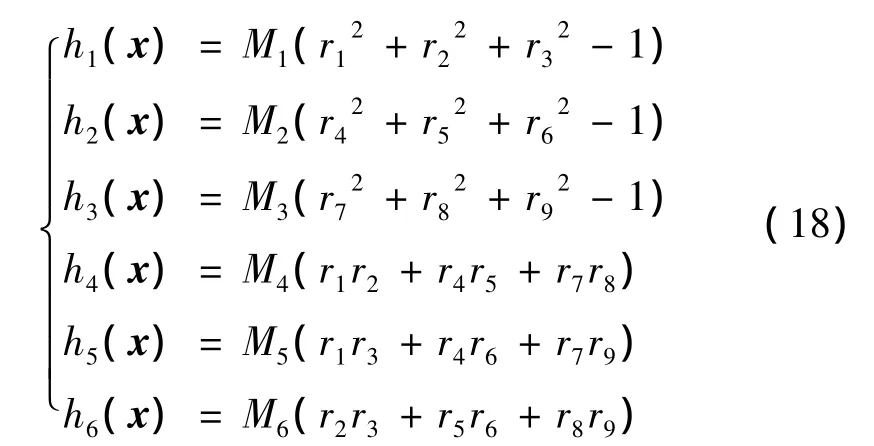
式中，M1～M6為罰因子，從而由被測點得到無約束最優化目標函數為:

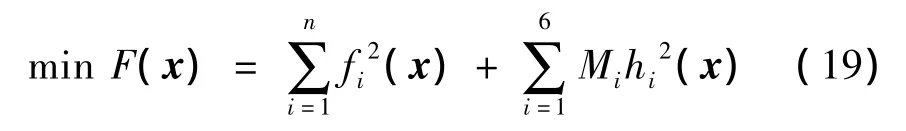
對空間若干點進行測量，當測點數n≥6時，利用高斯-牛頓法［13］可以求解出矩陣M1r中的參量值，即可知測站1坐標系o1-x1-y1-z1與測站2坐標系or-xr-yr-zr之間的位置關系。此時將測站1坐標系作為整個測量系統坐標系，將兩條視準軸方程統一到測站1坐標系o1-x1-y1-z1下，視準軸相交從而求得被測點坐標值。

3 模型仿真與實驗驗證

3.1 模型仿真

為了驗證數學模型的正確性，采用基于SOLIDWORKS與MATLAB的相結合的方法進行仿真。首先，根據建立的數學模型在SOLIDWORKS中進行坐標系實體構造并根據各構件連接關系建立裝配實體，如圖6所示。然后，從裝配實體中計算出需要的參量α，γ，r，R等。最后，根據水平度盤轉角和豎直度盤轉角，分別得出橫軸、視準軸、被測點的仿真數據。

Fig.6 Simulation structure of measurement model

根據構建的測量模型，得到參量 α1=α2=92°，γ1=γ2=80°，r1=r1'=r2=r2'=6.911mm，R1=R1'=R2=R2'=－6.911mm，測站1與測站2間轉換矩陣M1r如下:

改變模型中被測點的位置，求得相應的水平轉角和豎直轉角。通過數學模型，計算出被測點坐標(xs，ys，zs)，與直接從裝配實體得到的理論值(xt，yt，zt)進行比較。結果如表1所示。表1中的仿真結果驗證了數學模型的正確性。

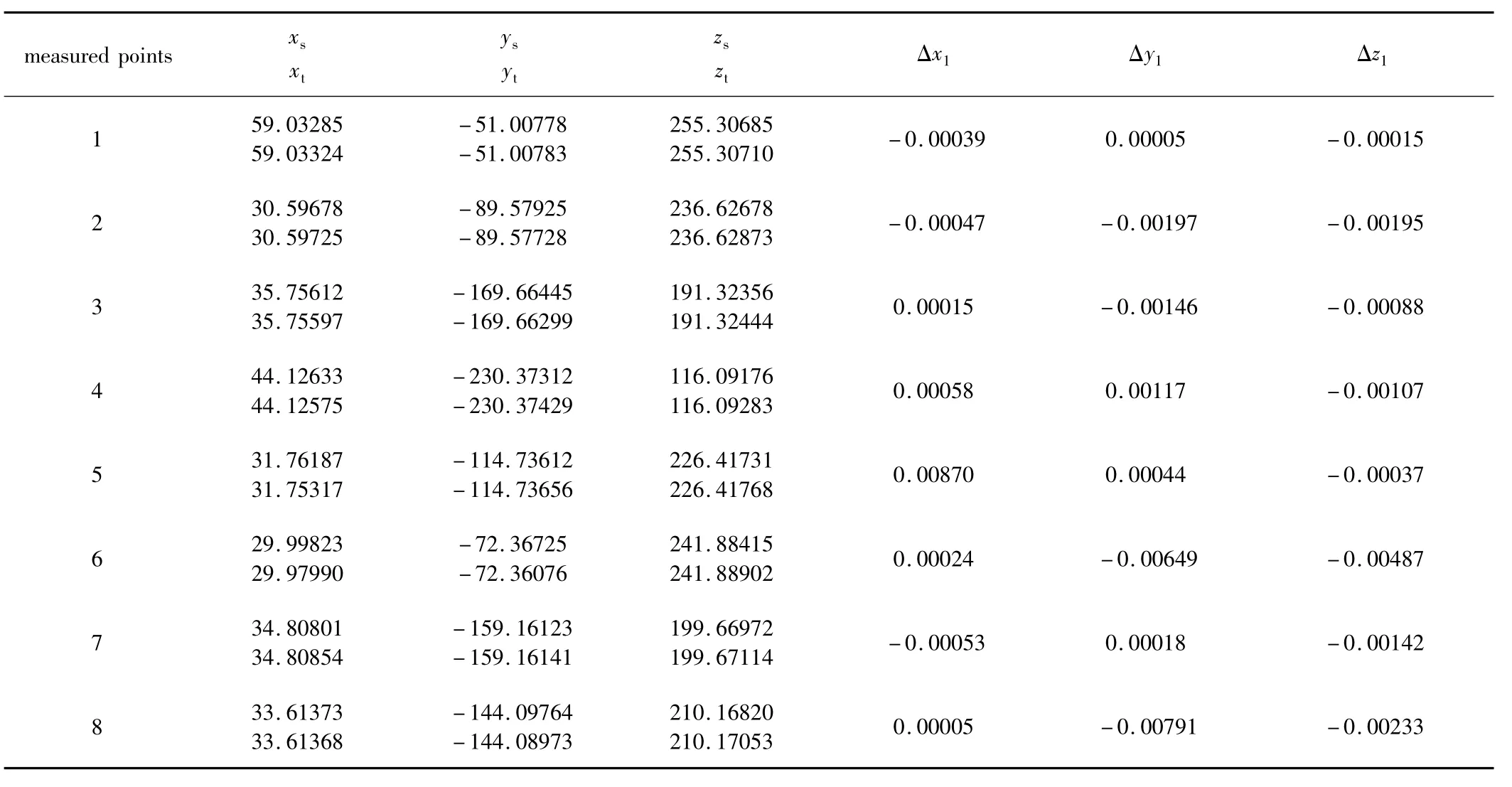
Table 1 Difference between the simulation values and the theoretical values/mm

3.2 實驗驗證

在上述的測量模型中，需要對2維云臺的一些參量進行提前標定。標定后，便可以通過測站1和測站2的水平角∠H和豎直角∠V得出視準軸方程，實現對被測點的測量。

以測站1為例，首先是坐標系o1-x1-y1-z1的建立。2維數字云臺由水平轉臺和豎直旋轉平臺組成。豎直旋轉平臺安放在水平轉臺上，而激光器安放在豎直旋轉平臺上。固定ZrO2陶瓷球(直徑2mm，精密等級G10，GB308-2002/ISO3290-1998)到水平轉臺上，控制2維云臺水平旋轉，使用Leica公司的激光跟蹤儀測量不同旋轉角時陶瓷球坐標。保持云臺在水平方向上固定，擬合出旋轉圓的圓心o1以及旋轉軸線的方向向量，旋轉軸線即為豎直軸o1y1。圓心o1與陶瓷球初始位置的連線設為o1x1軸。通過右手法則，確定出o1z1軸，坐標系o1-x1-y1-z1建立完畢。

然后，利用相同方法，擬合出俯仰旋轉軸的圓心o'和旋轉軸線的方向向量，旋轉軸線即為橫軸o'x'。根據軸線o'x'與o1y1的解析式，計算出點o'和B的坐標，以及軸線Bo'的解析式。根據以上條件，可以得到橫軸與豎直軸的固定夾角α1，Bo'與o1x1軸的夾角β1，橫軸與豎直軸的固定距離r1，垂足B與軸心o1的固定距離R1。當云臺旋轉時，可以得出橫軸o'x'在坐標系o1-x1-y1-z1的解析式。

最后，根據橫軸o'x'在坐標系o1-x1-y1-z1的實時方程，解算出坐標系o1-x1-y1-z1到動態坐標系o'-x'-y'-z'的矩陣Mr，并建立坐標系o'-x'-y'-z'。在坐標系o'-x'-y'-z'中，視準軸MN用準直激光束表示，其方程可通過測量激光束上的多點得到。根據以上條件，可以得到視準軸與橫軸軸的固定夾角γ1，DC與o'y'軸的夾角δ1，視準軸與橫軸的固定距離r1'，垂足D與軸心o'的固定距離R1'。

在參量標定完成之后，便可以通過建立的測量模型求解出被測點的坐標。

搭建的測量系統如圖7所示，主要由點激光器、高精度數字轉臺及PC機等組成，轉臺采用步進電機驅動，分辨率為 0.0125°。

Fig.7 Measurement system of non-orthogonal shafting laser theodolites

通過計算，得到實驗參量:α1=90.096546°，α2=88.904518°，γ1=92.490204°，γ2=89.370728°，r1=7.654343mm，r1'=108.755302mm，R1= －26.161574mm，R1'=11.211615mm，r2=6.399854mm，r2'=100.909601mm，R2= －30.206666mm，R2'=7.340672mm。測量空間中的多個點，利用高斯-牛頓法求解的測站1與測站2間轉換矩陣M1r如下式所示。

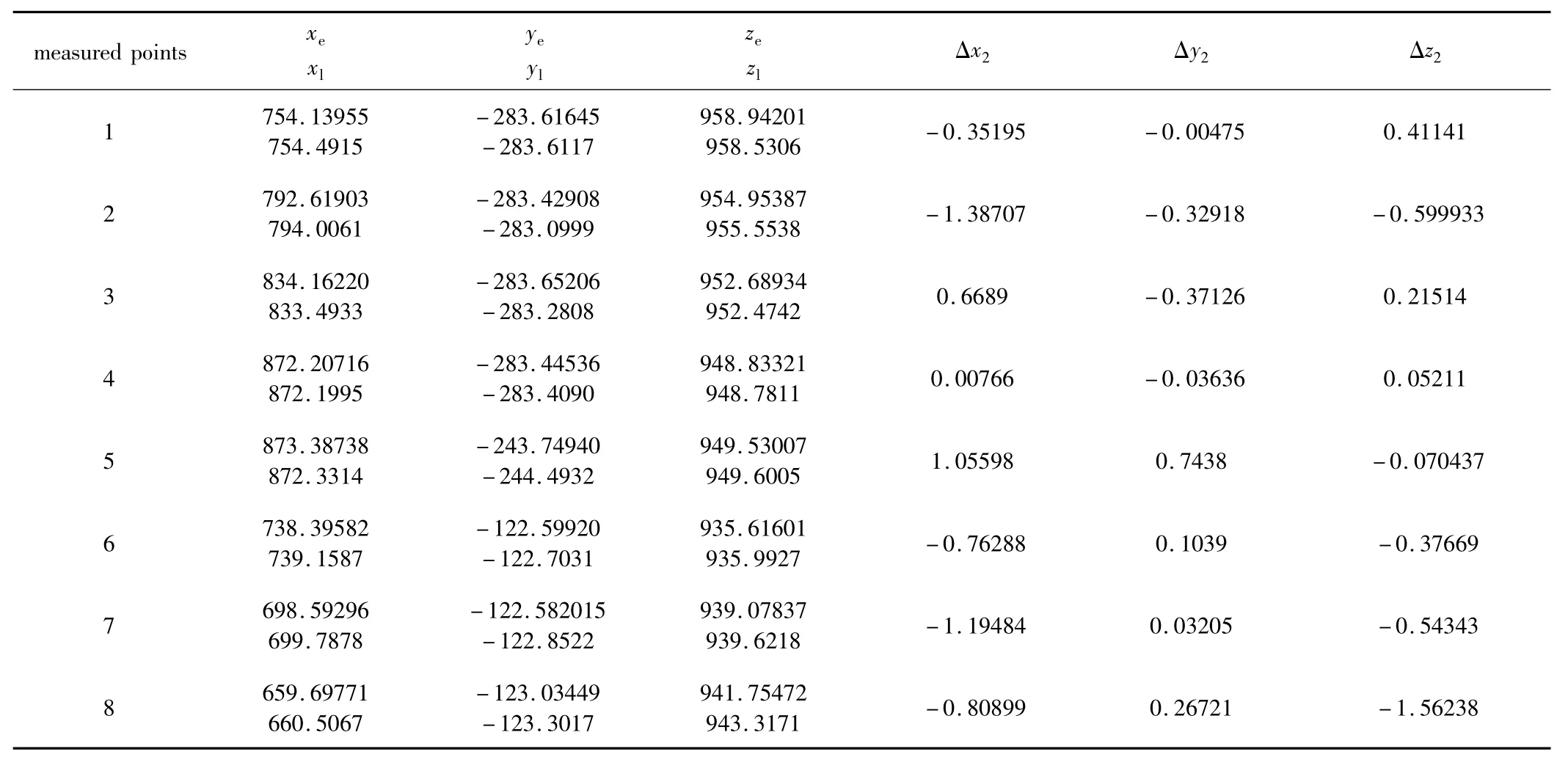
Table 2 Difference between the measured values and the standard values/mm

對目標點進行測量，把解算出的結果(xe，ye，ze)與激光跟蹤儀測得的標準值(xl，yl，zl)進行比對，其結果如表2所示。

由以上實驗數據可以看出，本系統成功地實現了對空間點3維坐標的測量。但由于云臺分辨率較低，引起了了較大的測量誤差。如當測量半徑R=5m時，云臺導致的最大測量誤差為δ=2πR×0.0125/360=1.09028mm，且此誤差隨著測量半徑的變大而變大。在實驗中，測量半徑為3m，被測點在拉依達準則下的測量不確定度達到±1mm以內，系統能滿足某些大尺寸測量場合的需要。

4 結論

針對大空間、大尺寸測量，在傳統經緯儀測量系統的基礎上，提出了一種新型的基于非正交軸系的激光經緯儀測量系統模型。該測量模型利用多臺激光經緯儀視準軸空間交匯，實現了對空間點3維坐標的測量。在測量半徑為3m時，被測點在拉依達準則下的測量不確定度達到±1mm以內，但測量不確定度會隨測量半徑的變大而變大。它克服傳統經緯儀正交軸系的結構要求、降低了系統成本、減少了誤差來源。但系統的精度還有待提高，需進一步優化測量模型;且測量過程完全手動，瞄準過程靠人眼，應提高自動化程度，以滿足工業現場大尺寸高精度快速測量的需要。

［1］ ZHANG Z L，ZHU J G，GENG N，et al.The design of double-theodolite 3-D coordinate measurement system［J］.Chinese Journal of Sensors and Actuators，2010，23(5):660-664(in Chinese).

［2］ WU B，WANG B.Automatic measurement in large-scale space with the laser theodolite and vision guiding technology［J］.Advances in Mechanical Engineering，2013，2013:629385.

［3］ TIAN L D，LIU C H，ZHAO J K，et al.Impact of three-axis error on angle measurement of photoelectric theodolite［J］.Infrared and Laser Engineering，2013，42(1):193-195(in Chinese).

［4］ LI G Y.Principle and development trend of non-orthogonal coordinate system［J］.Journal of Geomatics，2003，28(1):4-10(in Chinese).

［5］ HUANG G Y，LI G Y.Study of system orientation and coordinate calculation of IMS［J］.Acta Geodaetica Et Cartocgraphica Sinica，2003，32(3):256-260(in Chinese).

［6］ ZHOU H，ZHU J G，YE S H.The vision-based automatic collimation methodology of electronic laser theodolites for spatial coordinate［J］.Chinese Journal of Sensors and Actuators，2011，24(8):1205-1207(in Chinese).

［7］ GUO J Z.Research on high-precision 2-D turntable based on optical gratings［D］.Beijing:North China University of Technology，2013:2-10(in Chinese).

［8］ ZHANG X P，WANG J Q，ZHANG Y X，et al.Large-scale three-dimensional stereo vision geometric measurement system［J］.Acta Optica Sinica，2012，32(3):0315002(in Chinese).

［9］ ZHANG Z L，ZHU J G，YE S H，et al.The guidance methodology of a new automatic guided laser theodolite system［J］.Proceedings of the SPIE，2008，7160:806991.

［10］ ZHOU H，ZHU J G，YE S H，et al.Resolution improvement of the electronic eheodolite in automatic guided laser theodolite system by subdivided locating method of image［J］.Proceedings of the SPIE，2008，7160:807057.

［11］ XIAO Z T，ZHANG W Y，GENG L，et al.Accuracy analysis of binocular vision system［J］.Opto-Electronic Engineering，2014，41(2):6-8(in Chinese).

［12］ ZHANG G J.Vision measurement［M］.Beijing:Science Press，2008:134-166(in Chinese).

［13］ SHANG C，WANG G Q，CHEN G L.Test method of the absolute angle measuring system with inductosyn based on theodolite［J］.Chinese Journal of Sensors and Actuators，2008，21(5):865-868(in Chinese).