國債收益率曲線構建的案例教學研究

李 標，李曉燁

（中南財經政法大學 金融學院，湖北 武漢430073）

一、引言

國債收益率曲線不僅可為投資者提供投資的決策依據，也是貨幣政策和實體經濟之間、基準利率和市場利率之間的橋梁，為政府發行國債和實施政策提供依據。在利率市場化不斷推進的條件下，國債收益率曲線的重要性不言而喻。黨的十八屆三中全會中也明確提出了“需要不斷健全反映市場供求關系的國債收益率曲線”，同時該內容也是金融學專業核心課程《固定收益證券》教學的重點和難點。讓學生掌握收益率曲線的擬合方法更顯得尤為重要。

國債收益率曲線在過去的半個多世紀中，理論和實踐都有著突破性的發展，有不少的國內外學者對收益率曲線進行了研究。Nelson和Siegel（1987）提出了一種在表達式上與微分方程解非常相似，描述利率動態變化，該收益率曲線模型具有簡單靈活實用的特點。朱世武和陳健恒（2003）使用Nels on-Siegel-Svensson模型利用交易所債券數據成功估計了利率期限結構。陳芳菲和沈長征(2006)使用Nelson-Siegel模型提取了水平因素、斜率因素和曲度因素并擬合國債收益率曲線，進而又對收益率曲線進行預測。郭濤等（2008）根據國債交易數據用NS模型估計收益率曲線，并分析了模型的相關經濟學含義。胡志強等(2009)用NS模型擬合了國債收益率曲線，預測能力更強。陳艷等(2013)采用MATLAB擬合中國的利率期限結構曲線，對比了兩個參數精度和穩定性。

在當前環境下，金融產品層出不窮，如何科學地研究固定收益類證券類產品的風險收益顯得至關重要且越來越受到社會各界的重視。MATLAB語言由于具有編寫簡單、編程效率高、易學易懂等特點，可運用于定義國債的特征，滿足不同用戶計算需求，具有一定的實際意義。所以本文以案例教學的方式呈現matlab如何估計和擬合國債收益率曲線。本文第一部分為引言，第二部分介紹收益率曲線的理論和模型，第三部分基于MATLAB的案例部分，第四部分為結論。

二、國債收益率曲線的研究方法

研究擬合國家債收益率曲線的方法多種多樣，主要是依據交易所或銀行間市場的歷史數據進行分析，提取歷史數據的債券信息，并對曲線擬合和預測。在構造國債收益率曲線中，本文主要介紹直接方法、Nelson-Siegel方法以及多樣式樣條函數法。

（一）直接法

所謂直接方法，就是直接利用當前不同到期時間國債價格推導出到期收益率，并將計算所得的收益率進行線性聯結、繪制出相應的收益率曲線圖。這是一種較為簡單直觀的方法，假定債券各期的利息固定不變。

根據最基本的國債定價模型：

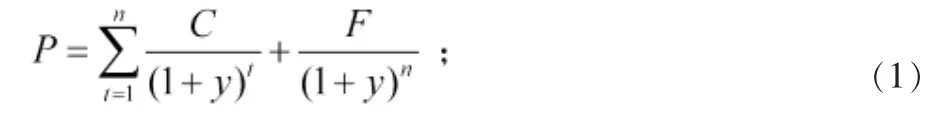
其中P為債券價格，C為各期利息，F為債券面值，y為到期收益率，n為債券年限。

（二）Nelson-Siegel模型

Ne1son-Siegel模型是NelsonC.和SiegelA.(1987)提出的一個參數擬合模型,該模型通過建立遠期瞬時利率的函數,從而推導出即期利率的函數形式。與樣條模型不同的是，它是對貼現函數的整條模擬,且需要估計的參數相對較少。它假設瞬時遠期利率函數為：

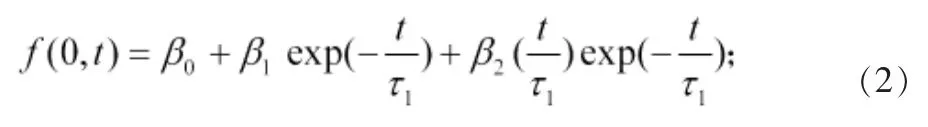
其中f（0，t）為即期計算未來t時點的瞬間遠期利率，β0、β1、β2以及τ1是待估計的參數。

根據 ，其中 是表示剩余到期限為t的連續復合利率，且t趨近于零時相當于即期利率。

即期利率函數形式為：

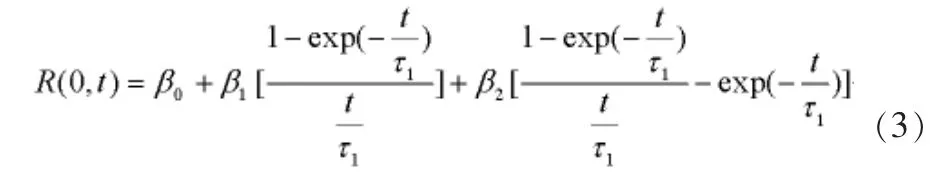
其中β0是當t趨于無窮時,函數的極限，故為長期因子，稱做水平因子；β1是t趨于0時,極限趨向于1，故為斜率因子；β2為曲度因子；τ1是比例參數,被解釋為短期利率向長期利率回轉的強度,可看作一個常數項。這個方程能夠產生大家所熟悉的遠期利率曲線的各種形狀,如單調型、水平和倒置型曲線。同時,經過后來學者的研究發現,該模型的參數都具有很明顯的經濟含義,使得模型本身容易被理解。

（三）Hermite插值模型

Hermite方法是數值計算領域里面函數逼近的一種重要方法,與前述樣條模型和NS及其擴展模型不一樣,Hermite模型并非曲線擬合模型,它只是一種插值技術。其構建利率期限結構的思路為:對解算出已知年期的即期利率,利用Hermite插值模型進行插值,得到相應的整條即期利率曲線。

Hermite插值模型具體描述如下：

Hermite插值法的到期限收益率曲線能夠通過所有的樣本點,對于收益率曲線的各種形態,該模型都能很好的予以反映。但該方法所需樣本點需經過專門挑選,且對樣本點的剩余期限有較嚴格的要求。對同一剩余期限,只能有一個樣本點。所以,該方法的實施需要一個專門的經驗豐富的團隊來進行,否則很容易出現偏差。目前,中國債券登記結算公司就是采用該法進行收益率曲線的估計。

三、基于Matlab的教學案例

（一）數據選擇

我國銀行間債券市場在1996年成立后，我國債券市場分割成為銀行間債券市場和交易所債券市場兩部分。與交易所債券市場相比，前者投資主體主要是機構投資者（商業銀行、保險公司、基金、證券公司、財務公司等），并且目前債券市場上最大的投資者商業銀行只投資于銀行間債券市場，同時市場上投資者的參與目的趨于資產配置而非資本投機，價格發現功能更強。更為重要的是，前者市場規模遠大于后者。

所以選取銀行間債券市場的國債債券數據，以2014年5月15日為基準。

（二）MATLAB估計收益率曲線

本小節會具體的介紹如何使用MATLAB進行收益率曲線的估計，將以案例教學的方式與讀者互動。在用MATLAB估計收益率曲線之前需要對一些變量進行闡述，Settle為交割日；Maturity為到期日；CleanPrice為凈價格；CouponRate為利率；Period為付息次數。

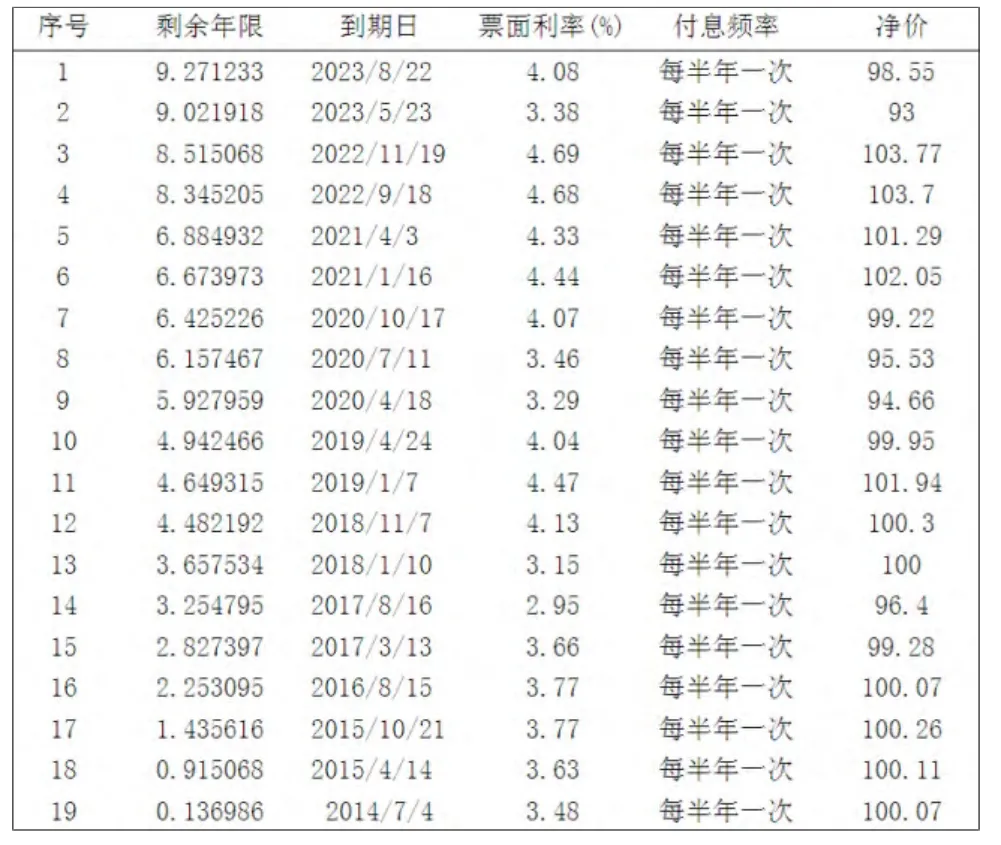
表1：債券信息

1.NS模型的實現

在MATLAB命令窗口輸入Settle=repmat（datenum（'date'），[N 1]）；date表示結算日，N表示債券個數。

接著輸入：Maturity=[datenum（'date1'）;datenum（'date2'）；datenum （'date3'）；datenum （'date4'）；...datenum（'dateN'）；]；date1到dateN分別表示N個債券的到期日，也就是它們的剩余期限。

再把債券的價格和利率導入，輸入如下命令：CleanPrice=[100.1；100.1；100.8；96.6；103.3；96.3]；CouponRate=[0.0400；0.0425；0.0450；0.0400；0.0500；0.0425]；

在將債券包含的信息集合在一起，輸入如下命令：Instruments=[Settle Maturity CleanPrice CouponRate]；

為了做圖的方便，需要把的幾個重要的節點找到，也就是按到期日從小到大排列，輸入命令：PlottingPoints=datenum（'date1'）:180:datenum（'dateN'）；

用命令bndyield計算收益率：Yield=bndyield（CleanPrice，CouponRate，Settle，Maturity）；

用IRFunctionCurve.fitNelsonSiegel命令即可估計NS模型的收益率：NSModel=IRFunctionCurve.fitNelsonSiegel（'Zero',datenum（'date'），Instruments）；

最后作圖：plot（PlottingPoints,NSModel.getParYields（PlottingPoints），'r'）；datetick（'x'）

2.樣條函數的實現

用1中方法得到債券的信息后，用IRFunctionCurve.fitSmoothingSpline命令估計樣條函數的信息：

SmoothingModel=IRFunctionCurve.fitSmoothingSpline('Forward'，datenum（'date'），...Instruments，@（t）1000）；

最后作圖即可：plot（PlottingPoints,SmoothingModel.getParYields（PlottingPoints），'b'）；datetick（'x'）

（三）收益率曲線的擬合

本文采用第1節的數據，通過第2節MATLAB命令先后用NS模型和Hermite樣條函數對收益率曲線進行擬合，即可得出模擬圖。

為了更好的研究它們的擬合程度，本文對它們的擬合情況與實際的收益率進行對比，如下圖1所示：

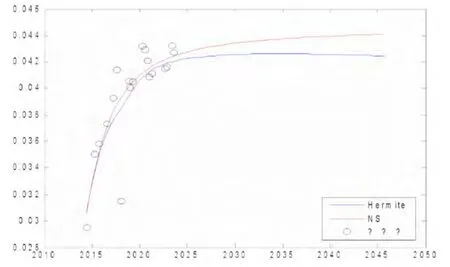
圖1：擬合效果對比圖

通過圖1可以看出NS模型和樣條函數擬合的方法還是有一定的差別，總體來看NS模型擬合的效果較好，也有部分債券的收益率擬合的不是很滿意，還需要進一步研究

四、結論

本文通過實際的案例操作，實現國債收益率曲線的構建，進一步的研究我國國債的利率期限結構的變化和影響。通過研究不同到期期限的銀行間國債收益率基本不難看出，隨著到期期限的逐漸增加，銀行間國債的收益率是逐漸增加的，即收益率曲線總體呈向上傾斜狀態，說明利率期限結構流通性偏好理論適用于我國銀行間國債市場。同時讓學生可以通俗易懂的理解《固定收益證券》這門專業課的重點和難點，更加生動的展示給學生復雜的過程和結果。

本案例教學的還可進一步增加其他函數形式或者模型對國債收益率曲線進行構建，更加豐富其教學的內容。

（注：本文系中南財經政法大學經濟管理實驗教學改革項目“國債收益率曲線構建與預期理論的實證檢驗”，項目編號：2013066）

[1]Nelson.C.R and A.F.Siegel.Parsimoniousmodeling of yield curves[J].Journal of Business，1987，（60）：473-489.

[2]孟繁慧.MATLAB在經濟數學教學中的應用[J].中國科教創新導刊,2013，（8）.

[3]林府標.淺談Matlab數值計算與微積分教學的幾點建議[J].教學教育論壇，2014，（4）.

[4]胡志強，王婷.基于Nelson-Siegel模型的國債利率期限結構預測[J].經濟評論，2009，（6）.

[5]陳蔚，馬駿馳，趙耀文.我國國債收益率曲線的實證研究[J].山東經濟，2011，（3）.

[6]鄭振龍，林海.中國市場利率期限結構的靜態估計[J].武漢金融，2003，（3）.

[7]郭濤,宋德勇.中國利率期限結構的貨幣政策含義[J].經濟研究，2008，（3）.

[8]王一鳴,李劍峰.我國債券市場收益率曲線影響因素的實證分析[J].金融研究，2005，（1）.

[9]陳艷，楊珺.基于Matlab背景下國債收益率問題探討[J].中國外資，2013，（9）.