基于信號博弈模型的交通誘導－路徑選擇分析

王中奇 馬 俊

（北京交通大學交通運輸學院1） 北京 100044） （北京信息科技大學機電工程學院2） 北京 100192）

0 引 言

交通誘導是一種非強制性的交通管理手段，交通管理者期望通過發布誘導信息合理地分配路網流量以使網絡整體出行費用最低，而出行者的目標是使個人出行費用最少.當網絡略去擁擠效應時Wardrop系統最優和用戶均衡是相等的［1］，而在網絡擁擠情況下交通管理者與出行者的目標并不完全一致.因此，在交通誘導系統中交通管理者與出行者之間存在一種博弈關系，兩者之間的互動決策過程會對路網交通流分布產生影響.博弈論很早在交通領域就有應用，Chen等［2］應用Cournot模型、Stackelberg模型和Monoply模型等，把動態交通控制和動態交通分配結合為交通管理者和出行者之間的非合作博弈；李艷君［3］在系統最優的原則下制定誘導與交通控制結合的交通管理策略，建立了以管理者為主出行者為從的Stckelberg模型；李學勇等［4］為實現路網流量的Nash均衡，建立了交通出行誘導離散Stackelberg動態博弈模型，并用逆向歸納法進行模型求解，進而得到用于網絡發布的誘導策略.上述相關研究中所建立的模型均為靜態博弈，交通領域的很多問題可以等價為非合作Nash均衡和Stackelberg博弈［5］.但是，在真實駕駛環境下出行者通常只能對當前所處路段的交通狀況有一個認識而很難獲知所處路網的交通狀態，出行者只能通過管理者所發布的誘導信息對路網的交通狀態做出判斷進而選擇出行路徑.靜態博弈模型不能體現真實路網中交通管理者與出行者之間的信息不對稱性，為此，劉建美等［6］提出誘導－出行信號博弈模型，并通過虛擬行動模型驗證了均衡解的合理性.交通管理者的誘導信息發布與出行者的路徑選擇之間的博弈關系符合不完全信息動態博弈中信號博弈模型所描述的情形，本文借助在信息經濟學領域廣泛應用的信號博弈模型來對兩者之間的博弈行為進行分析，并提出基于分離均衡點的誘導信息的分類方法，對誘導信息生成策略的研究提供了一種新的思路.

1 交通管理者與出行者之間的信號博弈模型

單個出行者對路網交通狀態的影響可以忽略，此處考慮的是路網同一OD對間具有一定數量出行者的集體行為特征.

1.1 模型假設和說明

1）采用交通擁堵指數（TPI）描述路網交通狀態，把路網狀態分為“暢通”“基本暢通”“輕度擁堵”“中度擁堵”“嚴重擁堵”5種.不同日期（工作日或節假日）不同時段同一路網各種交通狀態出現的概率是不同的，一般可以根據歷史數據統計得到.某些路網早晚高峰等特定時段“暢通”狀態出現的概率可以認為為0，且交通誘導對“暢通”路網運行狀況的改善作用有限，故本文不考慮路網“暢通”的情形.

2）管理者向使用者發布的誘導信息為誘導路徑和預期旅行時間.

3）隨著路網規模的增大，出行路徑迅速增加.對于具有一定規模的路網，可以近似認為交通管理者與出行者的策略在區間［0，1］是連續的.用M＝［0，1］之間的實數m來描述所發布的誘導信息，m＝0表示發布按隨機用戶最優分配的誘導路徑，以下簡稱隨機用戶最優路徑，m＝1表示發布按系統最優分配的誘導路徑，以下簡稱系統最優路徑；（0，1）間的實數m趨于0表示誘導路徑趨于隨機用戶最優，m趨于1表示誘導路徑趨于系統最優；出行者的策略空間用區間A＝［0，1］之間的實數a表示，a＝0表示出行者選擇隨機用戶最優路徑，a＝1表示出行者選擇系統最優路徑，（0，1）間的實數a趨于0表示出行者選擇路徑趨于隨機用戶最優路徑，a趨于1表示出行者選擇路徑趨于系統最優路徑.

4）出行者根據以往使用誘導信息的經驗建立對交通管理者的信任，交通管理者形成對出行者的信譽，交通管理者信譽越高出行者對誘導信息的服從率越高，誘導信息發布的效果越好.誘導路徑與出行者感知效用最大路徑的差異會影響服從率，兩者差異越大，誘導信息的服從率越低，這里將按隨機用戶最優分配的誘導路徑近似看作出行者感知效用最大路徑.交通誘導系統中交通管理者發布誘導路徑需要承擔信譽成本，所謂信譽成本就是發布高信號即趨于系統最優的誘導路徑之后，誘導信息服從率降低所造成的誘導效果減弱和由于信譽受損導致的管理者未來收益降低.信譽成本在某種程度上是一種預期信用損失.誘導路徑越是趨于系統最優，管理者承擔的信譽成本越高.

5）對于一定數量的出行者，所有出行者關于路網狀態的推斷是相同的，所有出行者都可以接收到管理者所發布的誘導信息.若無誘導信息發布，出行者按隨機用戶最優原則選擇出行路徑.

1.2 模型的建立

信號博弈是2個參與者之間的非完全信息動態博弈，在交通誘導信號博弈模型中的參與人是：交通管理者（信號發送者），記為S；出行者（信號接收者），記為R.本文建立的模型屬于多類型無限戰略博弈（4種交通狀態，參與人的策略空間為實數區間［0，1］），博弈的時間順序如下.

1）自然根據特定的概率分布p（ti），從可行的類型集 T＝｛t1，t2，t3，t4｝中賦予發送者某種類型ti，這里對所有的i，p（ti）＞0并且p（t1）＋p（t2）＋p（t3）＋p（t4）＝1.

2）發送者觀察到ti，然后從可行的信號集M＝［0，1］中選擇一個發送信號m.

3）接收者觀察到m（但不能觀察到ti），然后從可行的行動集A＝［0，1］中選擇一個行動a.

4）交通管理者與出行者的收益函數分別為Us（ti，m，a）和Ur（ti，m，a），且為雙方的共同知識.

其中：T＝｛t1，t2，t3，t4｝為類型空間，表示路網交通狀態，t1＝1為路網基本暢通，t2＝2為路網輕度擁堵，t3＝3為路網中度擁堵，t4＝4為路網嚴重擁堵.P（ti）為路網交通狀態為ti時的概率.這是一個3階段不完全信息動態博弈.首先，虛擬的局中人－自然決定當前路網的交通狀態；第二階段，交通管理者觀察到路網交通狀態并根據路網交通狀態發布誘導信息；第三階段，出行者根據交通管理者發布的誘導信息對路網交通狀態做出判斷并決定以何種程度接受誘導信息，進而做出路徑選擇.

2 效用函數性質分析

以往研究中，通常將交通流分配理論中系統最優和隨機用戶最優分配模型（或動態系統最優和動態隨機用戶最優分配模型）的目標函數分別作為交通管理者和出行者的收益函數，對于Stackelberg這類靜態博弈模型，可以通過逆向歸納的求解方法找出理想均衡點.但是不完全信息動態博弈的求解更加復雜，解決該類問題尚無有效算法，因此，上述目標函數的設定在信號博弈模型中不適合直接作為交通管理者與出行者的收益函數.本文用交通管理者與出行者的效用函數Us（ti，m，a）和Ur（ti，m，a）分別表示兩者的收益，效用函數的引入可以方便信號博弈模型的分析.這里Us（ti，m，a）表示交通管理者對誘導信息發布效果的滿意程度，Ur（ti，m，a）表示出行者對接收誘導信息后行動的滿意程度.

對于具有一定規模的路網，可以假設對于每個類型t，收益函數Us（ti，m，a）和Ur（ti，m，a）是關于（m，a）的連續函數.根據實際路網運行經驗Us（ti，m，a）和Ur（ti，m，a）具有以下特點：

1）在某一路網狀況下，若交通管理者的策略保持不變，出行者選擇的出行路徑越趨于系統最優，誘導信息發布的效果就越好，交通管理者的效用也越大，即給定0且為連續的.而在使用者策略不變的情況下，交通管理者發布的誘導信息越是趨于系統最優，其承擔的信譽風險越高，擔負的信譽成本越大，收益隨之減小，即且為連續的.假設出行者了解路網交通狀態，即完全信息條件下，出行者按隨機用戶最優原則選擇出行路徑，此時若管理者發布偏離該路徑不大的誘導路徑即小信號時，仍會有部分出行者受交通管理者積累的聲譽影響采納誘導信息，此時管理者效用是遞增的，即，ε＞0且足夠小.當信號m1足夠大即交通誘導路徑偏離隨機用戶最優路徑一定程度時，出行者對誘導信息服從率迅速降低使得交通管理者效用降低，即＜0.完全信息條件下，在小信號范圍內，相同信號改變量對路網運行狀態的改善作用逐漸減小；當發送的信號超過m1時，誘導路徑越趨于系統最優，誘導信息服從率下降的越快，所造成的交通管理者效用損失越大，所以誘導信息的邊際效益是遞減的，即0.交通管理者效用與發送信號之間的關系見圖1.

圖1 交通管理者效用－信號發送關系圖

2）系統最優解相對于用戶最優解，總出行費用的節約隨交通擁擠度的增加而增加［7］，因此路網越擁擠出行者對誘導信息的需求越高.對交通管理者來說，給定使用者的策略，擁擠路網誘導信息發布的效果較好，交通管理者發布誘導信息的邊 際 效 益 嚴 格 越 高，即＜；路網越擁擠，出行者相同程度的路徑選擇調整對路網運行狀態的改善效果越好，出行者的行為為交通管理者帶來的邊際效益遞增，即.對出行者來說，給定誘導策略，路網越擁擠出行者一定范圍內相同程度的路徑選擇調整會為其帶來更大的效用，即，但是隨著出行者的路徑選擇趨于系統最優，會造成部分出行者的收益降低，其行動為出行者整體帶來的邊際效用遞減，即0.

3）在出行者不了解道路交通狀態的情況下，交通管理者發送的信號越是趨于系統最優其承擔的信譽成本越大，為使管理者的收益保持穩定，需要出行者采取更積極配合的行動才能補償交通管理者因信譽成本增加所造成的損失，即≥0，at（m）是在交通管理者無差異曲線Us（t，m，a）＝C上接收者對類型t發送的信號m所采取的行動.在出行者了解道路交通狀態的情況下，路網越擁擠，出行者能夠改善自身出行的可調整的出行路徑越有限，因此出行者整體的最優路徑調整（，）程度越小，即0.atm為完全信息條件下，路網交通狀態為t時出行者的最優反應函數.

4）當t＝4路網嚴重擁堵時，發送趨于隨機用戶最優路徑的誘導路徑即小信號時，出行者的行動往往低于此時的效用最大行動，即出行者的路徑選擇較效用最大路徑更趨于隨機用戶最優路徑；而當發送超過m′的大信號時，交通管理者的信譽成本增大，若要保持管理者效用不變，出行者需要采取高于出行者效用最大行動的行動，所選路徑應更趨于系統最優以彌補發送大信號造成的損失.也就是說，存在信號m′發送者需要高于完全信息下的行動來補貼，如圖2高信號示意圖.

3 均衡點分析

交通管理者和出行者的之間的信號博弈模型應符合上述所做的分析，該模型滿足文獻［8］中對一類信號博弈模型的基本假設A1～A6.根據文獻［8］中的證明，該類信號博弈模型存在惟一的分離均衡.因此，本文所建立的交通管理者與出行者之間的信號博弈模型具有分離均衡且該分離均衡是惟一的，這在實際應用中是非常有意義的.

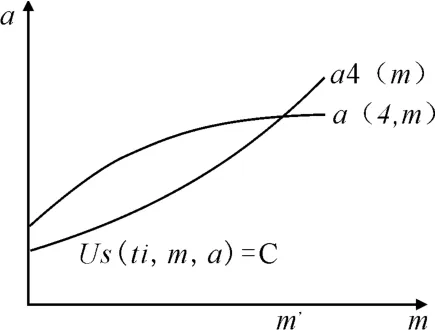
圖2 高信號示意圖

根據上述對效用函數性質的分析，交通管理者的效用函數可以表示為

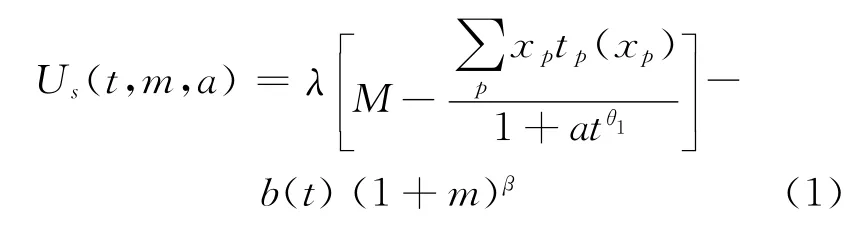
式中：λ為服從率；M 為一個足夠大的正數；xp為路段p的流量；tp（xp）為路段p上的阻抗；m為交通管理者發布的信號；a為出行者對交通管理者發布的信號做出的反應；t為路網交通狀態；θ1＞1，β＞1，兩者均與路網有關；0＜b（4）＜b（3）＜b（2）＜b（1）.

出行者的效用函數可以表示為

式中：Tmax為當前路網出行時間最長路徑的出行時間；Tfree為自由流最短路徑在當前路網的出行時間；θ2＞1與路網有關.

在完全信息條件下出行者的最優反應函數為

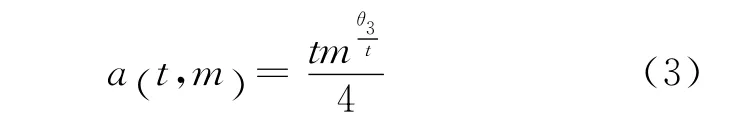
式中：θ3＞0與路網有關.記（）為類型一即基本暢通路網的分離均衡點，（）為類型二即輕度擁堵路網的分離均衡點，（）為類型三即中度擁堵路網的分離均衡點，）為類型四即嚴重擁堵路網的分離均衡點.［（），（），（），（）］為此信號博弈模型的惟一分離均衡.

4 結束語

本文提出了交通管理者與出行者之間的信號博弈模型，該模型能夠較好的描述出行者處于信息劣勢的條件下兩者的行為相互影響的過程.通過對建立的信號博弈模型的定性分析，得出了此博弈模型具有唯一分離均衡的結論.交通管理者可以通過信號傳遞幫助出行者對不同的路網狀況進行區分，并根據分離均衡點選擇發布相應的誘導信息，出行者可以據此選擇合適的出行路徑進而提高路網效率.交通管理者還可以根據分離均衡點對誘導信息進行分類，這為交通管理者制定誘導方案、發布誘導信息提供了新的理論方法.目前，對于不完全信息動態博弈問這類題尚無有效的求解算法，本文所建立的模型只涉及了相關問題的定性分析，下一步將對不同路網條件下效用函數的表示以及分離均衡的求解算法進行研究.

［1］黃海軍.城市交通網絡平衡分析理論與實踐［M］.北京：人民交通出版社，1994.

［2］CHEN O J，BEN A M E.Game＿theoretic formulations of interaction between dynamic traffic control and dynamic traffic assignment［J］.Transportation Research Record，1998，1617：179－188.

［3］李艷君.基于博弈論的交通控制與誘導一體化模型的研究［D］.天津：天津大學，2003.

［4］李文勇，陳學武，陸 建.交通出行誘導的離散Stackelberg動態博弈模型及其求解算法［J］.控制理論與應用，2009（10）：1157－1161.

［5］馬壽峰，卜軍峰，張安訓.交通誘導系統中系統最優與用戶最優的博弈協調［J］.系統工程學報，2005，30（1）：30－37.

［6］劉建美馬壽峰.交通誘導－出行信號博弈分析及其虛擬行動學習模型［J］.武漢大學學報：工學版，2010，43（1）：102－107.

［7］WIE B W，TOBIN R L.Comparison of system optimum and user equilibrium dynamic traffic assignments with schedule delays［J］.Transportation Research，Par t C：Emerging Technologies，1995，36：389－411.

［8］YU Gang，SHENG Zhaohan，XIAO Tiaojun.An effective algorithm for computing equilibrium outcome of class of signaling games［J］.International Journal of Information Technology ＆ Decision Making，2002，1（2）：209－228.