關于m-序列模加實現的自縮序列

王錦玲，鄒慧仙

WANG Jinling，ZOU Huixian

鄭州大學 數學與統計學院，鄭州 450001

School of Mathematics and Statistics,Zhengzhou University,Zhengzhou 450001,China

1 概述

自縮序列是一類重要的偽隨機序列，而周期和線性復雜度是序列偽隨機特性的經典度量。GF(3)上如何構造自縮序列的新模型使生成序列具有大的周期和高的線性復雜度，是研究序列密碼安全性的標準。

自縮序列由Meier 和Staffelbach[1]提出，由于自縮序列生成方式結構簡單，具有良好的偽隨機性，成為序列密碼研究的熱點；文獻[2-4]給出了比文獻[1]更好的周期和線性復雜度界值，但“自縮序列”的結構過于簡單，密鑰流選擇受到限制；基于此文獻[5-7]將“自縮序列”擴展在GF(3)上，得到的自縮序列比文獻[1-4]中有更高的周期和線性復雜度的界值，但以文獻[7]中“自縮序列”的生成方式為例。

若a∞=(a0,a1,a2…)是GF(3)上一n級m-序列，將a∞的輸出比特依次排列如下：

a∞=(a0,a1,a2)(a3,a4,a5)…(a3k,a3k+1,a3k+2)…

若a3k=0，則不輸出a3k所在括號內的所有比特；若a3k=1，則輸出a3k+1；若a3k=2，則輸出a3k+1，a3k+2，如此得到的序列記為SS3-序列。在文獻[7]中雖然當a3k=2時，輸出兩個比特對原有信息利用率低有所彌補，但當a3k=0 時，a∞收縮過快過多。本文在GF(3)上重構新型自縮序列模型，首次對輸出比特進行模加改變，根據模加數值來決定輸出比特，這樣得到的自縮序列周期上界為3n，下界為；線性復雜度上界為3n，下界為。而對于基于本原三項式和四項式的自縮序列的周期達到線性復雜度下界的概率改進為8 9 和5 6，比文獻[6]中自縮序列的平衡性強，信息利用率平穩，更好地彌補了文獻[7]中自縮序列收縮過快過多的不足，使得新型自縮序列保持原有序列大的周期和高的線性復雜度。

引理1設a∞=(a0,a1,a2…) 是GF(3) 上一n級m-序列，對于0 ＜k≤n，GF(3)上任意k元組(b1,b2,…,bk)在a∞的一個周期中出現的次數：

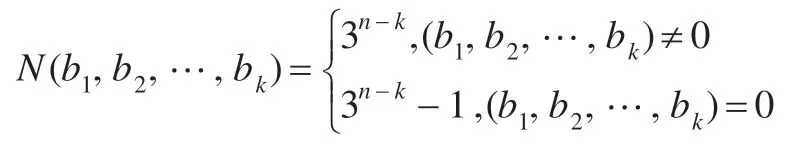
引理2設a∞=(a0,a1,a2…)是GF(3)上一n級m-序列，則有：

（1）序列a∞的最小周期是3n-1。

（2）序列a∞是平衡的，即在a∞的一個周期內，1、2各出現3n-1次，0 出現3n-1-1 次。

2 GF(3)上模加實現的自縮序列

2.1 模加實現自縮序列模型的構造

設a∞=(a0,a1,a2…)是GF(3)上一n級m-序列，將a∞的輸出比特依次排列如下：

a∞=(a0,a1,a2)(a3,a4,a5)…(a3k,a3k+1,a3k+2)…

若a3k⊕a3k+1=0，則不輸出a3k所在括號內的所有比特；若a3k⊕a3k+1=1，則輸出a3k+1；若a3k⊕a3k+1=2，則輸出a3k+1，a3k+2，這樣得到的序列z∞稱為擴展在GF(3)上a∞的模3-自縮序列，記為SS3(模3)-序列。

2.2 SS3(模3)-序列z∞的周期和線性復雜度

設a∞=(a0,a1,a2…)是GF(3)上一n級m-序列，將a∞的輸出比特依次分組如下：

(a0,a1,a2)…(a3n-3,a3n-2,a3n-1)(a1,a2,a3)…(a3n-5,a3n-4,a3n-3)(a3n-2,a0,a1)…(a3n-4,a3n-3,a3n-2)(a0,a1,a2)…

由此看到，把序列a∞的三個周期內輸出比特依次分組排列后，(a0,a1,a2)重復出現，因此SS3(模3)-序列z∞是周期的。由三元組組合的知識可得以下結論。

定理1設a∞=(a0,a1,a2…)是GF(3)上一n級m-序列，z∞為a∞導出的SS3(模3)-序列，則p(z∞)/3n。

定理2SS3(模3)-序列的最小周期。

由以上結果可以看出：SS3(模3)-序列z∞的周期和線性復雜度的界以3 的指數倍增加，保持了文獻[6]中SS3-序列的周期和線性復雜度。文獻[6]中自縮序列模型是根據a3k的取值來決定該括號內的輸出比特個數，而SS3(模3)-序列模型是根據a3k⊕a3k+1（模3）的取值決定該括號內的輸出比特個數，更好地彌補了a3k=0 時a∞收縮過快過多的不足，提高了原有的信息利用率，所得到的自縮序列整體上的平衡性更優。

3 GF(3)上本原三項式和本原四項式SS3(模3)-序列的周期和線性復雜度

3.1 基于本原三項式SS3(模3)-序列的周期和線性復雜度

下面考慮GF(3) 基于n次本原三項式f(x)=xn+c1xk+c0的LFSR序列，由此導出的SS3(模3)-序列的周期和線性復雜度。

定理3基于GF(3)上的n次本原三項式f(x)=xn+c1xk+c0，a∞是由f(x)生成的m-序列，又若在a∞導出的序列z∞中，至少出現長為的1-游程（或2-游程，或0-游程），則。

證明設，由定理2 知，即z∞中長為m的所有狀態都出現。又若在z∞中出現連續m+1 個1（或0 或2），在序列a∞的一個周期內至少出現了兩次，所以p(z∞)≥3m+1。

由定理1 知，p(z∞)/3n，因此。

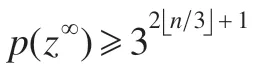
證明以下設。

n=3r：

（1）c0,c1都是1

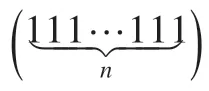
（2）c0=c1=2,k=3s或c0=1,c1=2,k=3s或k=3s+1

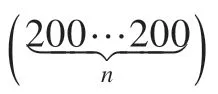
（3）c0=c1=2,k=3s+1或c0=2,c1=1,k=3s+1

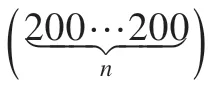
（4）c0=c1=2,k=3s+2

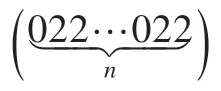
（5）c0=2,c1=1,且k=3s

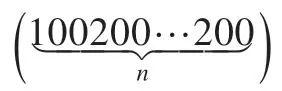
（6）c0=2,c1=1,且k=3s+2

在以下情形下：

（1）n=3r+1，c0,c1全部為1 或全部為2。

（2）n=3r+1，k=3s，c0,c1中有一個為1。

（3）n=3r+2，k是小于n的任意正整數。

均可適當選取a∞的n元初態，使得。

因此對于任意的n次本原三項式生成的LFSR 序列a∞所導出的對應自縮序列z∞，易得的概率約為8 9，且易得時，。

3.2 基于本原四項式的SS3(模3)-序列的周期和線性復雜度

下面考慮的GF(3) 上基于n次本原四項式f(x)=xn+c2xm+c1xl+c0(n＞m＞l)生成的LFSR 序列a∞所導出的SS3(模3)-序列z∞的周期和線性復雜度，雖然分析和計算上更加困難和復雜，但通過分析計算仍然可以得到z∞的周期和線性復雜度的下界，由于篇幅較長，這里只給出結論，不予證明。

定理5設f(x)=xn+c2xm+c1xl+c0(n＞m＞l)是GF(3)上的本原四項式，r是正整數，a∞是由f(x)生成的m-序列，z∞是由a∞導出的SS3(模3)-序列，在下列情形下，則p(z∞)≥3d+1，其中。

在下列情形下：

（1）n=3r，c0,c1,c2全部為2，m=3s或m=3s+2 且l=3h+2。

（2）n=3r，c0,c1,c2全部為1，m=3s+1，l=3h+2或m=3s+2，l=3h+1。

（3）n=3r,c0,c1，c2全部為1 或全部為2，m=3s，l=3h+1。

（4）n=3r,c0,c1，c2全部為1或全部為2，m=3s+1，l=3h或l=3h+1。

（5）n=3r，c0,c1,c2中有一個為2，m=3s，l=3h。

（6）n=3r，m=3s，l=3h+1，c0=2 或c1=2。

（7）n=3r，c1=2，l=3h+2，m=3s或m=3s+1。

（8）n=3r，c0,c1,c2中有一個為2，m=3s+1，l=3h+1。

（9）n=3r，c2=2，m=3s+2。

（10）n=3r，c0,c1,c2中有一個為1。

（11）n=3r+1,c0,c1，c2全部為1 或全部為2。

（12）n=3r+1,c0,c1，c2中有一個為2。

（13）n=3r+1,c0,c1，c2中有一個為1。

（14）n=3r+2，m，l是小于n的任意正整數。均可適當選取a∞的初態，得到p(z∞)≥3d+1。

從以上分析可以得出：當n=3r和n=3r+1 時，由任意的n次本原四項式生成的LFSR 序列a∞所導出的對應自縮序列z∞的周期的概率約為3 4，而當n=3r+2 時，的概率為1，因此對于任意的n次本原四項式生成的LFSR 序列a∞所導出的對應自縮序列z∞的周期的概率約為，易得當時，。

4 結束語

周期和線性復雜度是度量序列安全性的兩個重要指標，由以上結論可以看出：SS3(模3)-序列與文獻[7]中SS3-序列保持了相同的周期和線性復雜度下界，且均比文獻[5]中多位自縮MSS3-序列的周期和線性復雜度更優。GF( 3) 上基于本原三項式和四項式的LFSR 序列a∞導出的SS3-序列z∞的周期和線性復雜度的3 倍的概率分別為8 9 和5 6。由此模加實現生成的SS3(模3)-序列在模型構造上克服了多位自縮生成器生成序列在a3k=0時，收縮過快、過多的不足，序列平衡性更優。所以GF(3)上的模加實現的新型自縮序列是更適合流密碼應用的偽隨機序列。表1 將SS3(模3)-序列的周期、線性復雜度和收縮率與SS3-序列及MSS3-序列進行詳細比較。

表1 MSS3-序列、SS3-序列、SS3（模3）-序列對比表

由表1 可以看出新型自縮序列生成方式的改變，利用模加快速實現的方式使新型SS3(模3)-序列周期、線性復雜度和收縮率比文獻[6]更優，在保持文獻[7]SS3-序列的周期、線性復雜度界值和收縮率比例的情況下，對達到更優的周期、線性復雜度界值概率有進一步的改善；基于一般本原多項式的周期和線性復雜度更精確的界值，有待于尋求新的方法解決。

[1] Meier W，Staffelbach O.The self-shrinking generator[C]//LNCS 950：Advances in Cryptology Eurocrypt’94.Berlin：Springer-Verlag，1995：205-214.

[2] Blackburn S R.The linear complexity of the self-shrinking generator[J].IEEE Transactions on Information Theory，1999，45（6）：2073-2077.

[3] 張楠，戚文峰.基于三項和五項本原多項式的Self-Shrinking序列[J].信息工程大學學報，2004，5（2）：4-8.

[4] Kanso A.Modified self-shrinking generator[J].Computers and Engineering，2010，36（9）：993-1001.

[5] 王錦玲.多位Self-Shrinking 序列模型與研究[J].鄭州大學學報，1998，19（2）：119-122.

[6] 王錦玲，王娟，陳忠寶.GF(3)上多位自收縮序列的模型與研究[C]//密碼學進展-ChinaCrypt 2007.成都：西南交通大學出版社，2007：299-300.

[7] 王錦玲，陳亞華，蘭娟麗.擴展在GF(3)上新型自縮序列模型及研究[J].計算機工程與應用，2009，45（35）：114-119.

[8] 王錦玲，陳亞華，孫海峰.GF(q)上新型自收縮序列模型及研究[J].通信技術，2009，42（9）：74-76.