Gainse-Rescher 系統基于子代數的廣義重言式
李順琴,惠小靜
LI Shunqin,HUI Xiaojing
延安大學 數學與計算機科學學院,陜西 延安716000
College of Mathematics and Computer Science,Yan’an University,Yan’an,Shaanxi 716000,China
1 引言
廣義重言式理論是模糊邏輯的重要研究方向。自1998 年王國俊教授建立了修正的Kleene 系統和修正的Kleene 系統中的廣義重言式理論[1-2]后,其他多值邏輯系統中的廣義重言式理論也在蓬勃發展[3-12]。文獻[3-5]分別討論了修正的Go¨del 邏輯系統和Gainse-Rescher 邏輯系統中的廣義重言式理論,文獻[10]討論了修正的Go¨del邏輯系統中子代數的廣義重言式理論,文獻[11]討論了修正的Kleene 邏輯系統中子代數的廣義重言式理論。本文將Gainse-Rescher 邏輯系統中的廣義重言式理論進行推廣和補充,討論其序稠密子代數中的廣義重言式理論。
2 基本知識
定義1[1]設S={p1,p2,…}是可數集,?是一元運算,∨與→是二元運算,由S生成的(?,∨,→)型自由代數記作F(S)。F(S)中的元素叫公式或命題,S中的元素叫原子公式或原子命題。
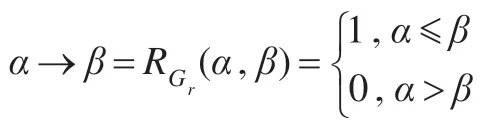
定義3設是[0,1]上的Gainse-Rescher 邏輯系統,E是的非空子集合,如果E關于中定義的?,∨,→運算封閉,則稱E是的子代數。
命題1E是的子代數當且僅當E在[0,1]中關于對稱且{0,1}?E。
證明(必要性)因為E是的子代數,所以由定義2 和定義3 知,對?x∈E,?x=1-x∈E,因此E在[0,1]中關于對稱。又由定義2 和定義3 知,對?x,y∈E,x→y的值是1或0,而E關于→運算封閉,故{0 ,1} ?E。
(充分性)由定義3 知,只需證明E關于中定義的?,∨,→運算封閉。由定義2 知E顯然關于∨運算封閉,又由于E在[0,1]中關于對稱,所以E關于?運算封閉。下證E關于→運算封閉。由定義2 知,對?x,y∈E,x→y的值是1 或0,而{0,1}?E,故E關于→運算封閉。
本文中提到的子代數都是指序稠密子代數,在不致引起混淆時將其簡稱為子代數。
定義4設E是的子代數,v:F(S)→E是映射,若v是(?,∨,→)型同態,即
v(?A)=?v(A),v(A∨B)=v(A)∨v(B)
v(A→B)=v(A)→v(B)
則稱v為F(S)在E中的賦值,其全體賦值之集記為Σ(E)。
定義5設A∈F(S),E為的子代數,α∈E:
(1)若?v∈Σ(E),v(A)≥α(v(A)>α),則稱A為E-α-重言式(E-α+-重言式),其全體之集記為α-T(E)(α+-T(E))。
(2)若A∈α-T(E),且?v∈Σ(E),v(A)=α,則稱A為可達E-α-重言式,其全體之集記為[α]-T(E)。
(3)若A∈α+-T(E),且?ε>0,?vε∈Σ(E),使得α<vε(A)<α+ε,則稱A為可達E-α+- 重言式,其全體之集記作[α+]-T(E)。
特別地,E-1-重言式簡稱重言式,其全體之集記為T(E)。
以上定義的各種重言式統稱為廣義重言式,在不致引起混淆時前綴“E-”將略去。
引理1設E是的子代數,,映射定義為:
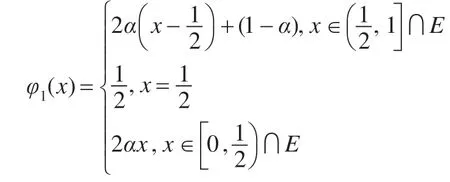
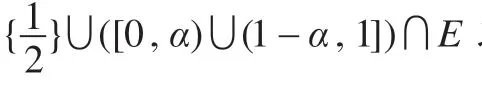
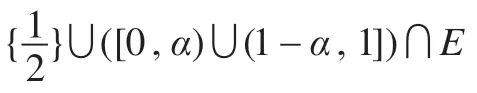
下面證明φ1保持?運算。
因此,由(1)~(3)可知φ1保持?運算。
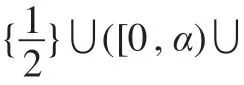
定理1設E是的 子 代 數,,則。
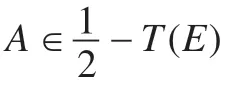
定理2設E是的子代數,,則α-T(E)=T(E)。
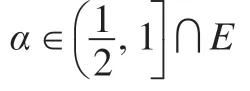
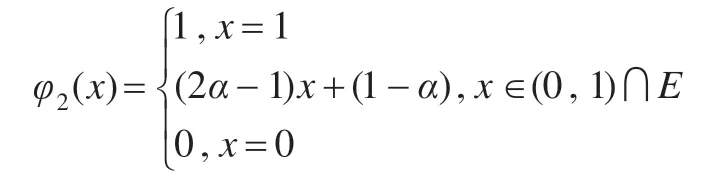
則顯然φ2是保序的雙射,易證φ2是同構的映射。事實上,φ2顯然保持∨運算和→運算,下面證明φ2也保持?運算。
當x=1 時,φ2(?1)=φ2(0)=0=?φ2(1);
當x=0 時,φ2(?0)=φ2(1)=1=?φ2(0);
當x∈(0,1)∩E時,φ2(?x)=(2α-1)(1-x)+(1-α)=-(2α-1)x+α?φ2(x) = 1-φ2(x) = 1-[( 2α-1)x+(1-α)] =-(2α-1)x+α所以φ2(?x)=?φ2(x)。因此φ2也保持?運算,這樣就證明了φ2是E與Uα之間的同構的映射。
設A∈α-T(E),則?v∈Σ(E),v(A)≥α。由于φ2是E與Uα之間的同構的映射,所以φ2v∈Σ(E),進而有φ2v(A)≥α且φ2v(A)∈Uα,從而只能φ2v(A)=1,由φ2的構造知v(A)=1,因此A∈T(E),即α-T(E)?T(E)。
定理3設E是的子代數,,則[α]-T(E)=?。
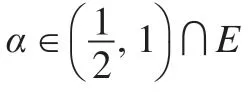
定理4設E是的子代數,,則α+-T(E)=T(E)。
證明若A∈T(E),顯然有A∈α+-T(E)。又若A∈α+-T(E),則?v∈Σ(E),v(A)>α。由定理2的證明過程知φ2v:F(S)→{0,1}∪((1-α,α)∩E)是同態的復合,因此φ2v∈Σ(E),進而φ2v(A)>α且φ2v(A)∈{0,1}∪((1-α,α)∩E),故φ2v(A)=1,由φ2的構造知v(A)=1,因此A∈T(E)。
用類似的方法結合定義5 和引理1 可證定理5。
定理5設E是的子代數,,則。
定理6設E是的子代數,,則[α+]-T(E)=?。
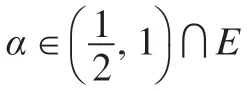
定理7設E是的子代數,α,β∈E且α≠β,則:
[α]-T(E)∩[β]-T(E)=?
[α+]-T(E)∩[β]-T(E)=?
[α]-T(E)∩[β+]-T(E)=?
[α+]-T(E)∩[β+]-T(E)=?
證明若[α]-T(E)∩[β]-T(E)≠?,不妨設α>β,取A∈[α]-T(E)∩[β]-T(E),則?v∈Σ(E),v(A)≥α且v(A)≥β,注意到α>β,所以?v∈Σ(E),v(A)≥α。而由A∈[β]-T(E)知存在v0∈Σ(E),使得v0(A)=β<α,矛盾。所以[α]-T(E)∩[β]-T(E)=?。
其余各式用類似方法可證。
定理8設E是的子代數,則關于E而言F(S)有如下的分劃:
證明(1)由定義5 知集族中任意兩成員之交為空集,且由定理3 和定理6 可知它們的并集是F(S),因此只需驗證它們均為非空集合即可。
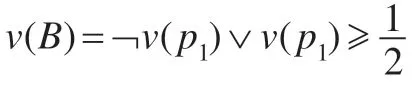
v(C)=1-v(A)=0,因此C∈[0]-T(E)。
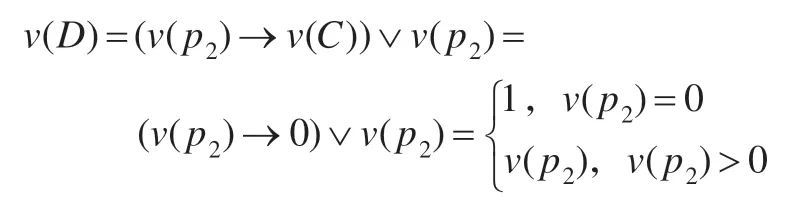
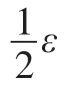
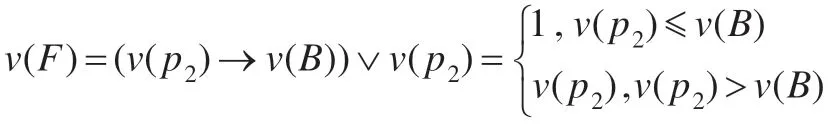
(2)可類似證明。
4 結論
本文將廣義重言式理論進行推廣和擴充,討論了Gainse-Rescher 邏輯系統中基于序稠密子代數的廣義重言式理論,并利用可達廣義重言式概念在的序稠密子代數中給出公式集F(S)的一個分劃。關于Gainse-Rescher 邏輯系統中離散子代數上的廣義重言式理論,將另文討論。
[1] 王國俊.修正的Kleene系統中Σ-(α-重言式)理論[J].中國科學:E 輯,1998,28(2):146-152.
[2] 王國俊.非經典數理邏輯與近似推理[M].北京:科學出版社,2000.
[3] 吳洪博.Go¨del 邏輯系統中的廣義重言式理論[J].模糊系統與數學,2000,14(4):53-59.
[4] 吳洪博.Go¨del 系統中一種降級算法及性質[J].四川大學學報:自然科學版,2003,40(6):997-1001.
[5] 吳洪博,閻滿富.Gainse-Rescher 邏輯系統中的廣義重言式理論[J].四川大學學報:自然科學版,2000,37(5):675-682.
[6] 王龍春,王國俊.R0-代數[0,1]的子代數與廣義重言式[J].數學學報,2004,47(3):521-526.
[7] 黃阿敏,裴道武.系統RDP 中的廣義重言式理論[J].模糊系統與數學,2010,24(4):6-11.
[8] 裴道武.積邏輯系統中的廣義重言式[J].模糊系統與數學,2002,16(4):19-27.
[9] 劉練珍,李開泰.修正的Product邏輯中的廣義重言式理論[J].模糊系統與數學,2005,19(1):12-17.
[10] 李順琴,王國俊.修正的Go¨del 邏輯系統中子代數的廣義重言式理論[J].計算機工程與應用,2008,44(36):58-60.
[11] 魏海新.修正的Kleene 邏輯系統中子代數的廣義重言式理論[J].計算機工程與應用,2009,45(22):32-33.
[12] 李修清.Go¨del 邏輯系統中1/2-子代數上的廣義重言式理論[J].計算機工程與應用,2011,47(5):43-45.

