基于PAM和MRD的新型六維寬頻隔振系統及其特性

，

(河南科技大學 機電工程學院， 河南 洛陽　471003)

引言

軍用車輛、艦艇、飛機等經常處于路況顛簸、海面風浪拍擊、氣流襲擾、炸彈襲擊等惡劣環境中，極易導致車載/艦載/機載精密設備受到三維平移及三維旋轉方向的強烈振動，然而這些精密設備只有在振動極其微弱甚至沒有振動的環境中才能正常工作，振動和沖擊稍大或稍多一些就容易導致設備無法工作，甚至失效。因此要保障這些精密設備的可靠運行及其生命力，就必須進行六維寬頻隔振。

六維隔振系統容易產生剛度耦合、阻尼耦合，這給剛度阻尼的設計帶來了困難，其次系統需要支撐一定的載荷，但系統的變形范圍有限，因此系統剛度不能無限減小，從而阻礙了隔振頻率的降低，除此以外，剛度和阻尼不易調節，大多數隔振材料或隔振器的剛度和阻尼不能隨隔振頻率的變化而改變，這就限制了系統的寬頻隔振能力。

針對六維隔振很多學者做了卓有成效的研究，Wada等[1]利用立方構型的Stewart機構實現了解耦，并采用主動控制方法實現了高精度的振動隔離和抑制。Thayer和Campbell等[2]在此基礎上對其設計進行了改進，增大了系統可控制的振動幅度。張春良、梅德慶等[3]提出了一種以空氣彈簧為被動隔振元件、超磁致伸縮致動器為主動隔振元件的微制造平臺六自由度隔振系統， 通過主動控制方式實現了高性能隔振。楊慶俊等[4]提出了一種能實現衛星六自由度隔振的氣動八作動器隔振平臺，并進行了主動控制研究。石奇端、馬履中等[5]在減振裝置中采用六自由度并聯機構作為基體，在原動件處輔以可控彈簧阻尼系統，較好地解決了多自由度減振問題。李坤全[6]提出了一種基于6-RSS并聯機構的六維減振系統，并利用主動控制方法提高隔振能力。

本研究則提出了一種基于氣動肌肉和磁流變阻尼器的六維寬頻隔振系統，該系統可實現剛度阻尼的解耦，可利用氣動肌肉、磁流變阻尼器實現剛度、阻尼的調節，能通過改變機構參數大幅降低支撐頻率。

1　六維隔振系統

圖1為處于工作平衡位置時的六維隔振系統，基座上固定有3個按圓周均布的基架，在基架與中間懸架之間通過球鉸并聯9個氣動肌肉和6個磁流變阻尼器，在中間懸架與載荷支撐平臺之間通過球鉸并聯6個氣動肌肉和3個磁流變阻尼器。氣動肌肉的剛度可通過調節進氣壓力進行調節，磁流變阻尼器的阻尼參數可通過調節輸入電流進行調節，整個機構是全對稱的。

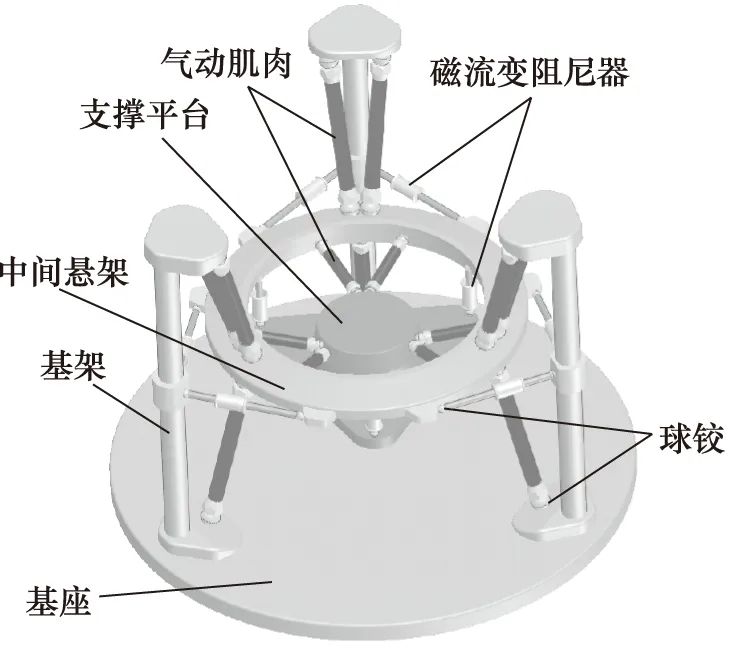
圖1　六維隔振系統外觀圖

1.1　氣動肌肉并聯設計

氣動肌肉并聯機構主要為載荷/支撐平臺提供恢復力和支撐力，處于工作平衡位置時，其機構如圖2所示，該機構是全對稱的。其中，點B1、B2、B3在半徑為R的圓周上均布，點B4、B5、B6在半徑為r的圓周上均布，弧A10B1、A11B1、A12B2、A13B2、A14B3、A15B3所對的圓心角皆為30°，氣動肌肉A1B1、A2B1、A3B1、A4B2、A5B2、A6B2、A7B3、A8B3、A9B3與相應的過B1、B2、B3點的分布圓切平面之間的空間夾角均為μ，且滿足0<μ<2°，氣動肌肉A1B1與A2B1之間、A4B2與A5B2之間、A7B3與A8B3之間的空間夾角均為γ，且滿足0<γ<4°，氣動肌肉A10B4、A11B4、A12B5、A13B5、A14B6、A15B6與中間懸架圓平面之間的空間夾角均為σ，且滿足σ<2°，另外A1B1、A2B1、A3B1、A4B2、A5B2、A6B2、A7B3、A8B3、A9B3這9個氣動肌肉的長度均為Lw，A10B4、A11B4、A12B5、A13B5、A14B6、A15B6這6個氣動肌肉的長度均為Ln。

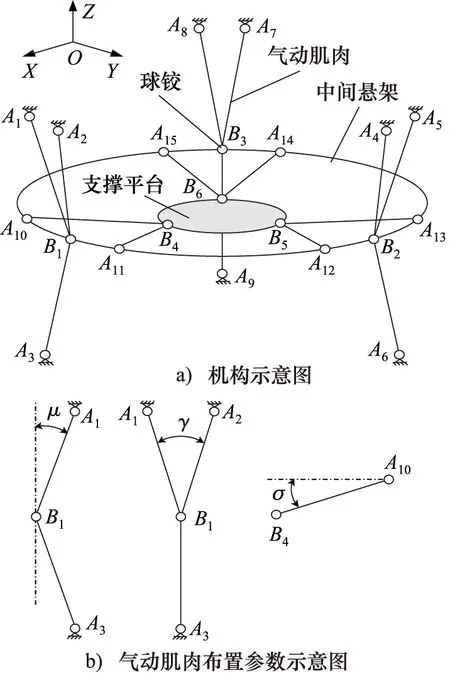
圖2　氣動肌肉并聯機構

1.2　磁流變阻尼并聯設計

磁流變阻尼并聯機構主要為系統提供阻尼力，耗散系統能量，處于工作平衡位置時，其機構如圖3所示，該機構是全對稱的，磁流變阻尼器C1D1、C1D2、C2D3、C2D4、C3D5、C3D6與中間懸架圓平面共面，且長度相同，弧D1D2、D3D4、D5D6所對的圓心角均為2α，C1、C2、C3所在的分布圓半徑為d，磁流變阻尼器C7D7、C8D8、C9D9皆平行Z軸。

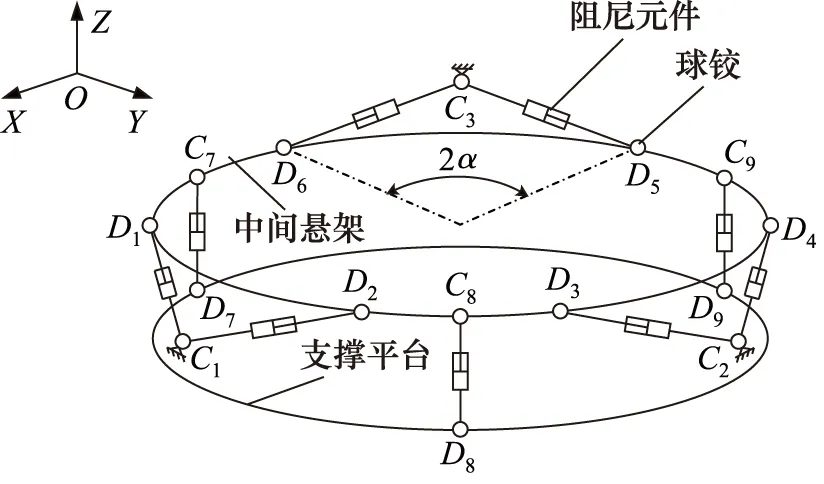
圖3　磁流變阻尼并聯機構

2　系統雅可比

2.1　氣動肌肉子系統的雅可比

系統處于工作平衡位置時，根據運動學理論可求得氣動肌肉并聯機構的由氣動肌肉作用空間到支撐平臺笛卡爾六維空間的雅可比矩陣(假設γ、μ、σ很小)。

2.2　磁流變阻尼子系統的雅可比

系統處于工作平衡位置時，同樣根據運動學理論可求得磁流變阻尼并聯機構的由磁流變阻尼器作用空間到支撐平臺笛卡爾空間的雅可比矩陣。

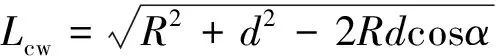
3　載荷/支撐平臺振動方程

設支撐平臺處于工作平衡位置時基架與中間懸架之間的上層6個氣動肌肉的剛度均為kw，下層3個氣動肌肉的剛度均為kwd，中間懸架與支撐平臺之間的6個氣動肌肉的剛度均為kn；基架與中間懸架之間的6個磁流變阻尼器的阻尼系數均為cw，中間懸架與支撐平臺之間的3個磁流變阻尼器的阻尼系數均為cn；載荷質量為m，其在慣性坐標系O-XYZ中的慣量矩陣為diag{Jx,Jy,Jz}，假設支撐平臺和中間懸架的質量遠小于載荷質量，可忽略不計。根據功能計算原理，可分別求得隔振系統在工作平衡位置的慣性、剛度及阻尼矩陣:

M=diag{m,m,m,Jx,Jy,Jz}

(1)

kwd,kn,kn,kn,kn,kn,kn}Jk

(2)

6R2d2cwsin2α/(R2+d2-2Rdcosα)}

(3)

由式(1)～式(3)顯見，系統的剛度及阻尼矩陣是解耦的，而通過合理地放置載荷可實現慣性矩陣的解耦，因此整個隔振系統此時是完全解耦的。

設支撐平臺在慣性坐標系O-XYZ中的振動位移為:

基座在慣性坐標系O-XYZ中的振動位移為:

假設載荷/支撐平臺作小位移振動，忽略非線性因素，則載荷/支撐平臺的振動方程可寫為:

(4)

4　寬頻隔振原理及彈性阻尼元件參數計算

由于系統的慣性、剛度及阻尼都是解耦的，因此容易根據式(1)～式(4)將系統解耦成單自由度系統而分別得到沿X、Y、Z軸平移以及繞X、Y、Z軸旋轉方向的固有頻率:

(5)

(6)

(7)

(8)

(9)

(10)

對于任一方向的單自由度系統而言，若基座作頻率ω的簡諧振動，則系統的振動位移傳遞率(振幅比)為:

(11)

根據式(11)可得η與ξ、λ之間的關系曲線，如圖4所示。

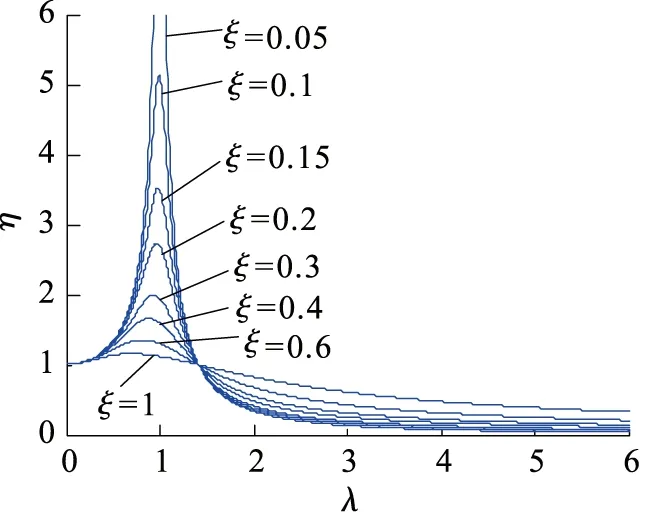
圖4　η與ξ、λ之間的關系曲線

由式(5)～式(10)顯見，減小kw、kwd、kn、γ、μ、σ就能降低各方向的固有頻率，然而由于載荷需要支撐，且氣動肌肉伸縮空間有限，因此其剛度不能無限減小。對于中間懸架與基架之間的9個氣動肌肉而言，下層3個不能起到支撐作用(只起穩定作用)，其剛度kwd可以任意小，而上層6個將起支撐作用，由于γ、μ很小，根據靜力學原理有:

6kwδw=mg

(12)

其中，δw為中間懸架與基架之間上層6個氣動肌肉的靜變形量。

因為所允許的氣動肌肉的伸縮空間有限，因此要求:

δw≤δwmax

(13)

其中，δwmax為相應氣動肌肉所允許的最大靜變形量。

所以結合式(12)、式(13)可得到這6個氣動肌肉的最低剛度:

kwmin=mg/(6δwmax)

(14)

對于支撐平臺與中間懸架之間的6個氣動肌肉而言，也要起到支撐作用，由于σ很小，則根據靜力學原理有：

1.人生三截草，不知哪截好。（人有旦夕禍福，人生也難以預測，將人生幾個階段比喻成三截草，不知道哪個階段生活會怎么樣。）

6σknδn=mg

(15)

其中，δn為支撐平臺與中間懸架之間6個氣動肌肉的靜變形量。

同樣由于氣動肌肉伸縮空間的限制，因此要求:

δn≤δnmax

(16)

其中，δnmax為相應氣動肌肉所允許的最大靜變形量。

所以結合式(15)、式(16)可得到該6個氣動肌肉的最低剛度:

knmin=mg/(6σδnmax)

(17)

將式(14)、式(17)確定的kw、kn代入式(5)～式 (10)可得:

(18)

(19)

(20)

(21)

(22)

(23)

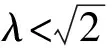
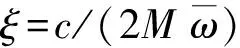
(24)

(25)

(26)

(27)

(28)

(29)

則根據式(24)～式(29)及阻尼比的取值ξ=0.1～0.3即可確定基架與中間懸架之間6個磁流變阻尼器的阻尼系數cw，以及中間懸架與支撐平臺之間3個磁流變阻尼器的阻尼系數cn。

5　結論

針對車載/艦載/機載精密設備的隔振需求，本研究提出了一種六維隔振系統，通過分析得出該系統具有三個特點： ① 剛度及阻尼解耦，因此能大大降低系統參數的設計與計算的復雜度，容易實現各方向性能均衡的隔振； ② 剛度和阻尼可調，支撐頻率可大幅降低，因此能隔離超低頻的振動， 進而實現寬頻隔振； ③ 阻尼布置的優化，提高了各方向阻尼的有效性。所以該系統具有一定的實用價值。

參考文獻：

[1]WADA B K, RAHMAN Z, KEDIKIAN R, et al. A Vibration Isolation, Suppression and Steering (VISS)[J]. Journal of Intelligent Material Systems and Structures, 1996, 7(2): 241-245.

[2]THAYER D, CAMPBELL M, VAGNERS J, et al. Six-axis Vibration Isolation System Using Soft Actuators and Multiple Sensors[J]. Journal of Spacecraft and Rockets, 2002, 39(2): 206-212.

[3] 張春良,梅德慶,陳子辰.微制造隔振平臺振動的模糊廣義預測控制[J].機械工程學報,2007,43(12):194-201.

[4]楊慶俊,王曉雷,鄭鋼鐵.氣動八作動器隔振平臺的主動隔振研究[J].應用力學學報,2007,24(3):339-342.

[5]石奇端,馬履中.六自由度并聯機構組合彈簧阻尼減振裝置[J].農業機械學報,2007,38(8):128-131.

[6]李坤全.6-RSS并聯機構在六維主動減振平臺中的應用研究[D].北京：北京交通大學,2008.