內流式閥件中的空化抑制新方法探究

　,

(中國艦船研究設計中心, 湖北 武漢　430064)

引言

空化噪聲和氣蝕現象在液壓元件中十分常見。其產生的根本原因是，當局部壓力低于飽和蒸氣壓時，液體中的氣核子長大形成空泡。空泡遇到高壓潰滅，產生壓力輻射，進而形成噪聲和腐蝕元件壁面[1～3]。

國內外許多學者通過流場分析和實驗手段對空化影響因素進行了研究，發現影響空化的最直接因素是流場壓力分布[4]。基于這一結論，一些學者通過改進液壓元件局部結構來改善壓力分布達到抑制空化的目的。Heron[5]改進傳統錐閥、滑閥閥口后部流道的剖面形狀使得流束在閥口下游形成穩定旋渦，旋渦離心力促使氣泡向渦核聚集以避免潰滅，從而降低噪聲。Hisanori[6]等對比例溢流閥噪聲進行了研究，發現具有環形流道及二級阻力結構的閥流道有抑制空化噪聲的效果。張鐵華[7]等設計了二級圓錐式閥口結構，并與一級圓錐式節流閥口進行對比，由于二級節流總的壓差由2個節流口分擔，使得每級進出口壓力比值變小，空化系數σ值變大，所以二級節流的抗氣蝕性能比一級節流的抗氣蝕性能好。弓永軍[8]等從流場控制的角度，研究先導式純水溢流閥抑制氣汽蝕方法。指出高壓引流結構使出口旋渦流由于受高壓射流的影響而明顯后移，旋渦中心的壓力升高從而大大降低了汽蝕發生的可能。杜學文[9]綜合利用二級節流及回流增壓原理設計改進了節流閥閥芯結構，改善了節流槽下游的壓力分布，使空化程度得到很大程度的抑制。

基于通過改善流場壓力分布來抑制空化的基本思想，本研究提出：將內流式閥件出口壓力引至節流口處，提高節流口下游壓力，達到抑制空化的效果。為將出口壓力引至節流口處，對內流式閥件的閥腔進行了改進(如圖1)。本研究主要是通過數值分析的方法對改進閥腔結構抑制空化進行驗證和對改進閥腔結構的抑制空化效果進行研究。

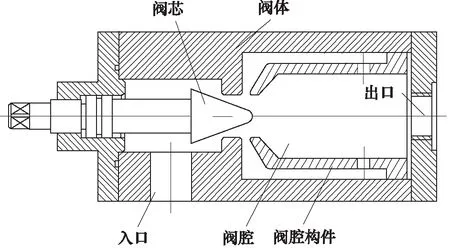
圖1　內流式閥件中閥腔改進結構示意圖

1　空泡群模型

液壓元件中的空泡一般呈空泡群出現，空泡群由許多的單個空泡構成。和單空泡一樣，空泡群經歷了生長發育、潰滅兩個階段[10～12]。在生長發育階段，節流口處產生的單個空泡隨流體流向低壓區，在下游集結成為空泡群；在潰滅階段，空泡群流向高壓區，空泡群快速潰滅且消失。

1.1　空泡群生長發育階段

在生長發育階段，空泡群中的單空泡之間相互影響小，因此可以用單空泡運動來模擬空泡群運動并用單空泡參數估計空化群半徑和空化百分數。單空泡運動用Rayleigh-Plesset方程[13]描述如下：

(1)

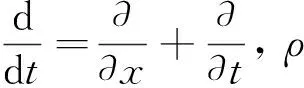
1) 空泡群半徑估計

空化區內產生的空泡都隨流體到下游，聚集成為空泡群。因此可以認為空化區域的體積等于空泡群的體積。空化區域的體積可以表達為式(2)，空泡群的體積表達為式(3):

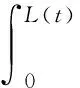
(2)

(3)

由式(2)、式(3)得,空泡群的半徑為：

(4)

式中，L(t)是指t時刻空化區域的長度。

2) 空泡群空化體積百分數估計

假設流體中的氣核子半徑大小相等且均勻分布, 且發育后的空泡群中的單空泡半徑大小也相等且均勻分布，同時單空泡之間的間距等于氣核子之間的間距。若用l表示氣核子之間的間距，則單位體積內空泡所占體積比，即空泡體積百分數為：

(5)

1.2　空泡群潰滅階段

文獻[14]指出，在計算空泡群潰滅壓力時，考慮空泡間的相互作用和沒考慮空泡間的相互作用的計算結果相差2個數量級，因此考慮空泡間的相互作用對空泡潰滅壓力的影響是有必要的。M?rch[10,11]假設空泡群是球形，構成空泡群的空泡均勻分布且大小相等，并引入空泡百分數和空泡間相互影響系數，將Rayleigh-Plesset空泡運動方程改進為空泡群模型:

(6)

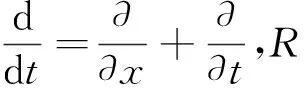
M?rch[10,11]認為單個球形空泡有0%～50%的能量輻射到空泡群。Wang[12]指出空泡間相互影響的系數由β、R0、a0有關，并且當β(1-β)(R0/a0)2<1時，空泡間的影響忽略不計，但當β(1-β)(R0/a0)2>>1時，這個值越大，空泡間相互影響越大。依據β(1-β)(R0/a0)2越大，γ取值越大且不能超過0.5的特點，故可定義空泡間相互影響的系數:

(7)

式中,K是比例因子。

1.3　空泡群潰滅壓力

根據文獻[10]、[11]經驗公式，空泡群潰滅時產生的潰滅壓力為:

(8)

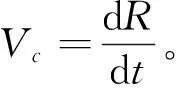
2　數值方法

假定空泡與流體之間沒有相對運動, 因此空泡在空間運動位移可以描述為x=u(x,t)t。又假定流體處于定常流狀態，空泡在空間運動速度可以簡化為u(t)，所以x可以簡化成只與時間t有關的函數。有理由可以推出，p(x,t)可以寫成只與時間t有關的函數p(t)=p(x(t),t)；空泡半徑a(x,t)和空泡群半徑R(x,t)也可以寫成只與時間t有關的函數a(t)=a(x(t),t)，R(t)=R(x(t),t)。因此空泡生成運動方程(1)和空泡群潰滅運動方程(6)可以分別改寫成方程(9)、(10)：

(9)

(10)

為了求解空泡群模型，需要知道空泡群周圍的壓力。本研究利用CFD仿真軟件求解閥腔流場,并獲得沿流運動方向上的平均壓力pavg(x)和平均速度uavg(x)。用CFD進行流場計算時，選擇RNGk-ε湍流模型進行計算求解，同時選擇入口壓力和出口壓力作為邊界條件。

然后，根據Δx=uavg(x)Δt,xn+1=xn+uavg(xn) Δt，利用插值和擬合的方法可以求得位移x與時間t的關系x(t)。用x(t)代替x代入壓力pavg(x)中可以獲得壓力pavg和時間t的關系pavg(t)。用pavg(t) 代替式(9)、(10)中p(t)，并用MATLAB 求解常微分方程(9)、(10)。

3　計算結果與討論

為了驗證圖1所示的閥腔結構是否能抑制空化以及評估抑制空化效果如何，采用了將未改進閥腔結構流道A和改進閥腔結構流道B(如圖2所示)兩種情況下空泡群的大小和空泡群潰滅壓力進行對比分析的方法。

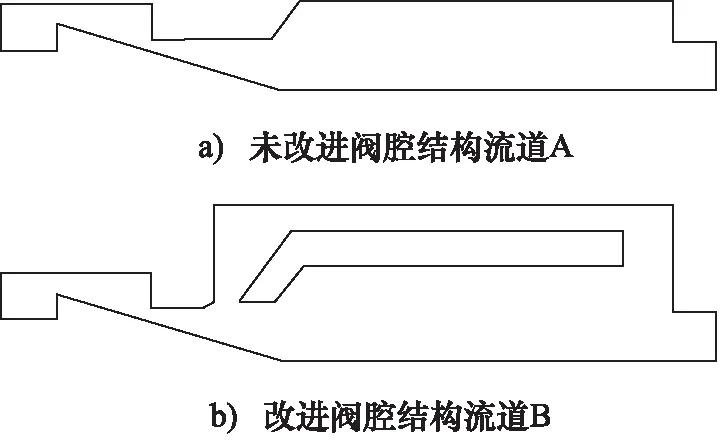
圖2　對比分析圖

3.1　抑制空化的有效性驗證

本小節的目的是，驗證提出的將出口壓力引至節流口處達到抑制空化的效果的想法。選擇一組數據：入口壓力p1=10 MPa，出口壓力p2=0.5MPa，按照上文所提到的方法進行計算。

由表1可以得知，流道B中產生的空泡群的半徑R和空泡群潰滅壓力pc均小于流道A中產生的空泡群半徑R和空泡群潰滅壓力pc。這是因為改進的閥腔結構將出口壓力引至節流口處，提高了節流口及其下游的壓力(如圖3所示)，壓縮了空泡群發育空間和縮短了空泡群發育的時間。由此可以得出：將出口壓力引至節流口處能夠達到抑制空化的目的。

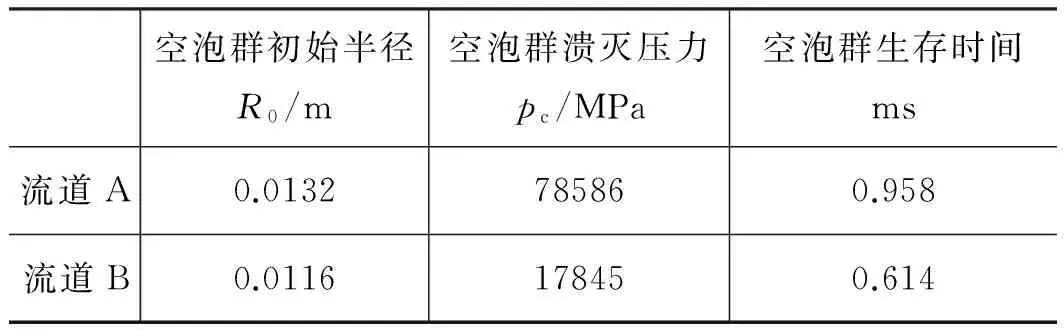
表1　空泡群大小、空泡群潰滅壓力

3.2　入口壓力的影響

圖4、圖5分別是出口壓力p2=0.5 MPa時，不同入口壓力情況下的空泡群半徑和空泡群潰滅壓力曲線。由圖可知，在入口壓力p1等于或者小于6 MPa時， 流道B中產生的空泡群的初始半徑R0和空泡群潰滅壓力pc都等于0， 沒有產生空化。隨著入口壓力p1的增大， 流道A和流道B中的空泡群初始半徑R0和空泡群潰滅壓力pc都逐漸增大，這與文獻[14]中的結論相似。但流道B中的空泡群初始半徑R0和空泡群潰滅壓力pc始終小于流道A中的空泡群初始半徑R0和空泡群潰滅壓力pc，流道B中的空泡群潰滅壓力pc曲線較流道A中曲線平緩。

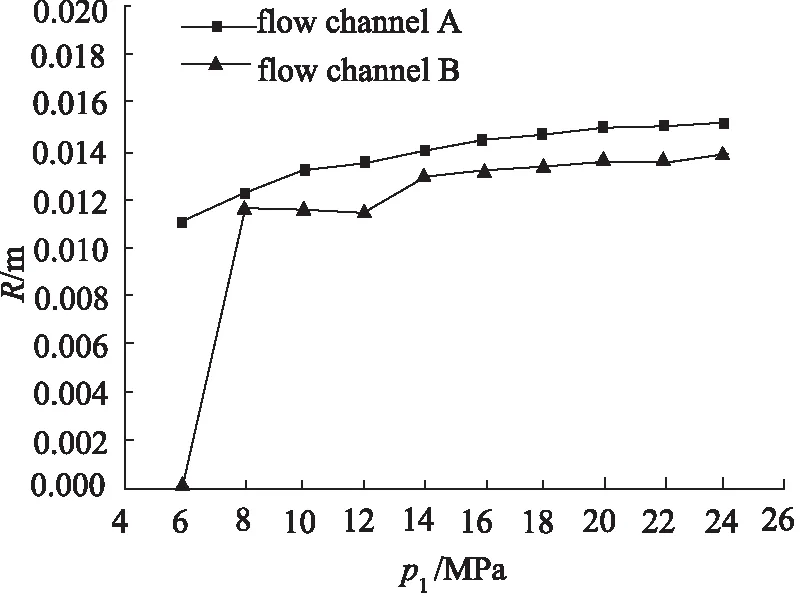
圖4　出口壓力p2=0.5 MPa 時，不同入口壓力情況下的空泡群半徑R

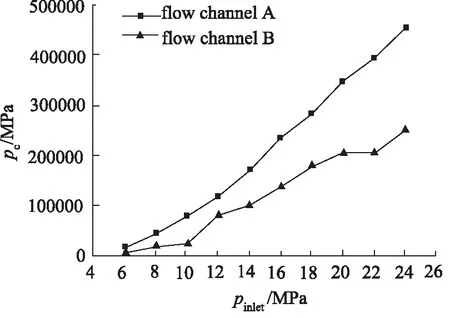
圖5　出口壓力p2=0.5 MPa 時，不同入口壓力情況下的空泡群潰滅壓力pc

本研究定義了流道B和流道A中的空泡群潰滅壓力之比η=pcB/pcA來描述改進閥腔的抑制空化效果，并且當η越小，表示抑制空化的效果越好。

圖6是出口壓力p2=0.5 MPa時不同入口壓力情況下η曲線。由圖可知，η曲線大體上是隨著入口壓力的增加而增大，但在p1=10 MPa處有輕微轉折，η開始減小，然后在p1=12 MPa處突然上升，最后，η曲線趨于平緩。總體來說，隨著入口壓力的增大，改進閥腔結構的抑制空化能力減弱，但最后趨于穩定。

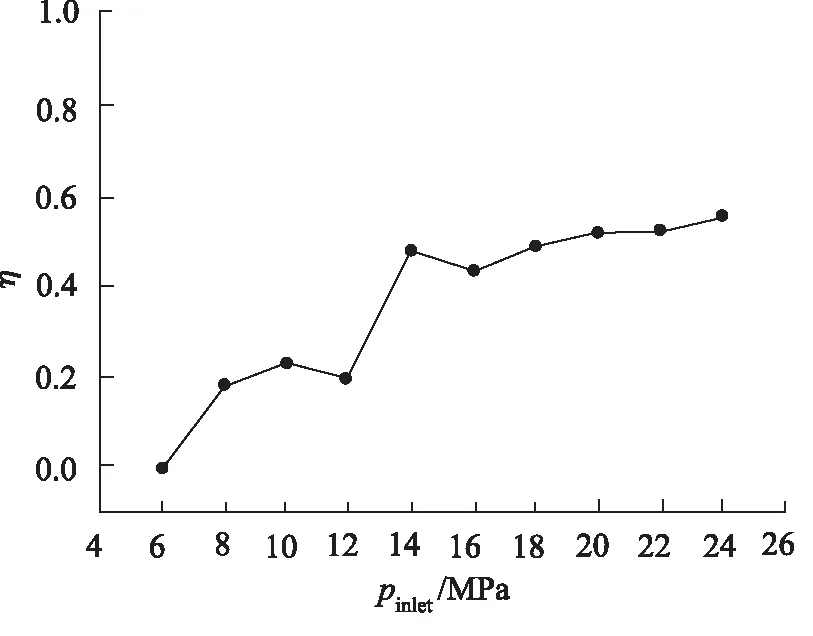
圖6　出口壓力p2=0.5 MPa 時，不同入口壓力情況下η曲線

3.3　出口壓力的影響

圖7、圖8分別是入口壓力p1=10 MPa時，不同出口壓力情況下的空泡群半徑和空泡群潰滅壓力曲線。由圖可知，在出口壓力p2等于或者大于0.7 MPa時，流道B中空泡群的初始半徑R0和空泡群潰滅壓力pc都等于0，即沒有產生空化。隨著出口壓力p2的增大，流道A和流道B中的空泡群初始半徑R0和空泡群潰滅壓力pc都逐漸減小， 這與文獻[14]中的結論相似。

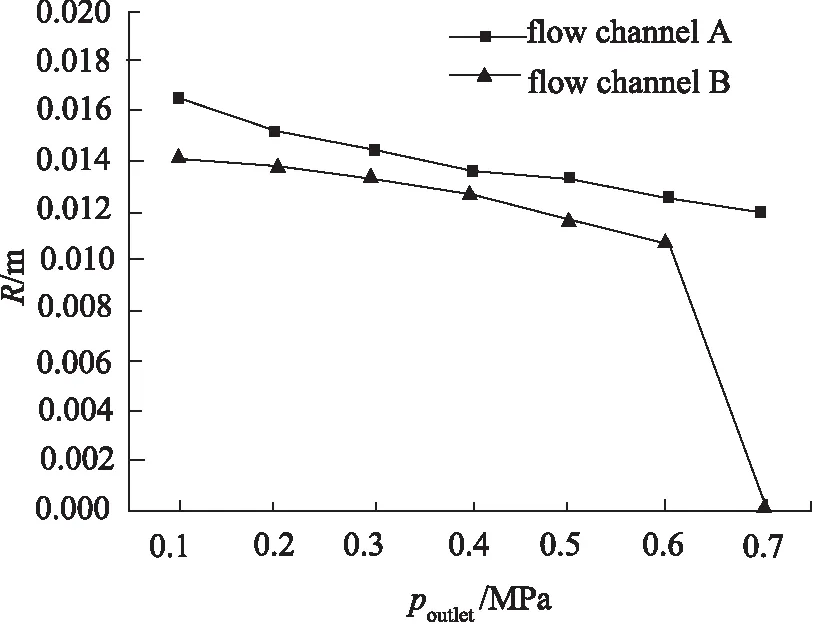
圖7　入口口壓力p1=10 MPa 時，不同出口壓力情況下的空泡群半徑R

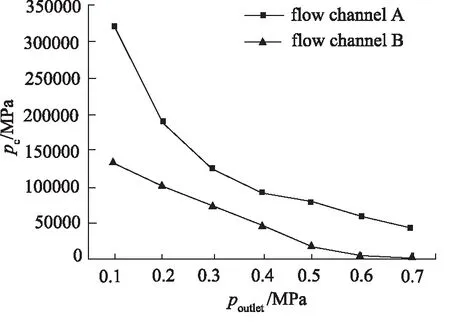
圖8　入口口壓力p1=10 MPa 時，不同出口壓力情況下的空泡群潰滅壓力pc

但流道B中的空泡群初始半徑R0和空泡群潰滅壓力pc始終小于流道A中的空泡群初始半徑R0和空泡群潰滅壓力pc。

圖9是入口壓力p1=10 MPa時，不同出口壓力情況下η曲線。由圖可知，在出口壓力p2=0.1 MPa～0.3 MPa時，η曲線隨著出口壓力的增加而增大，但當p2>0.3 MPa時，η開始減小，并且直至p2=0.7 MPa，η減為0。這說明：隨著出口壓力的增大，改進閥腔結構的抑制空化能力增強，且最后完全抑制了空化的產生。

圖9　入口口壓力p1=10 MPa 時，不同出口壓力情況下η曲線

4　結論

為了驗證和研究提出的將閥出口壓力引至節流口處來抑制空化的想法，首先建立了內流式閥件的空泡群模型，然后結合CFD計算獲得的壓力場與速度場，并運用數值計算方法和對比分析方法研究了不同壓差下帶改進閥腔和不帶改進閥腔的節流閥中的空化。得到以下結論：

(1) 將出口壓力引至節流口處可以達到抑制空化的效果；

(2) 隨入口壓力增加，改進閥腔的抑制空化能力逐漸減弱，但最后趨于穩定；

(3) 隨出口壓力的增加，總體來說，改進閥腔的抑制空化能力逐漸增強，直至完全抑制空化。

參考文獻：

[1]L Lu, J Zou， X Fu. The Acoustics of Cavitation in Spool Valve with U-notches [J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2012, 226：540-549, DOI: 10.1177/095441001

1413221.

[2]董方，李曉謙，張敏.鋁熔體中超聲輻射桿的空蝕實驗及機理研究[J].華中科技大學學報(自然科學版), 2015, 2(43): 85-88.

[3]D Maynes, G J Holt, J Blotter. Cavitation Inception and Head Loss Due to Liquid Flow Through Perforated Plates of VaryingThickness[J]. ASME J. Fluids Eng., 2013,135(3)：03130201.

[4]冀宏,傅新,楊華勇，等. 節流槽型閥口噪聲特性試驗研究[J]．機械工程學報，2004，40(11)：42-46.

[5]HERON H A. The Control of Cavitation in Valve[C]. England:7th International Fluid Power Symposium,1986：275-283.

[6]UENO H. Noise Measurement and Numerical Simulation of Oil Flow in Pressure Control Valves[J]. JSME International Journal, Series B, 1994, 37(2) ：336-341.

[7]張鐵華，楊友勝，李壯云．二級圓錐式節流閥口的設計及實驗研究[J]．液壓與氣動，2001，(11)：12-15．

[8]弓永軍，周華，楊華勇．閥芯結構對純水溢流閥抗汽蝕特性的影響研[J]．農業機械學報，2005，36(8)：50-54．

[9]杜學文．液壓閥口空化機理及對系統的影響[D]．杭州：浙江大學，2008．

[10]M?rch K A. Energy Considerations on the Collapse of Cavity Clusters[J]. Journal of Applied Scientific Research, 1982,(38):313-321.

[11]M?rch K A.On Cavity Cluster Formation in a Focused Acoustic Field[J]. Journal of Fluid Mech,1988,(201):57-76.

[12]Y Wang. Numerical Computation of Shock Waves in a Spherical Cloud of Cavitation Bubbles[J]. Transactions of the ASME Journal of Fluids Engineering,1999,(121):872-880.

[13]Kevin J. Farrell. Eulerian/Lagrangian Analysis for the Prediction of Cavitation Inception[J]. CAV2001:sessionA1.003, 2001:1-8.

[14]冀宏. 液壓閥芯節流槽氣穴噪聲特性研究[D]. 杭州：浙江大學，2004.