高速內嚙合齒輪軸減速器扭轉振動傳遞矩陣法分析

　，

(北京航空航天大學 自動化科學與電氣工程學院， 北京　100191)

引言

減速器是傳動系統的重要組成部分。齒輪嚙合過程的激勵特性，系統所傳遞的動力特性以及輸出端負載特性，必然會激起傳動系統的振動以及傳動系統和機匣(箱體)結構間的相互耦合振動[1]。減速器傳動系統的動力學特性會對其工作性能的實現和工作可靠性產生重要的影響，國內外均對各類減速器傳動系統動力學特性的研究高度重視。扭轉振動會給傳動系統帶來重大問題，甚至導致災難性后果[2]。高速齒輪減速器的扭轉振動分析，給系統的可靠性和優化設計等研究提供有力支撐。

從已有的研究看，目前對于齒輪傳動系統的扭轉振動分析通常有兩種方法：有限元方法(FEM, Finite Element Method)和傳遞矩陣方法(TMM， Transfer Matrix Method)[3]。有限元法通過二階微分方程建立轉子軸承系統，具有計算精度高，更能貼近曲軸實際工作情況等特點，但因其計算規模巨大，通常被用于系統的控制設計和估計[4]。而傳遞矩陣法通過將鏈狀傳動結構離散化成為一系列集中慣量、集中剛度的集總參數模型，因其分析計算鏈式結構振動快捷有效等特點，被廣泛用來解決動力學問題[5,6]。

文獻[7]利用傳遞矩陣法分析直升機旋翼試驗臺傳動系統的振動特性，找到了系統自激振動產生的原因，發現振動發散與試驗臺主軸支撐剛度有關。文獻[8]研究表明，增加軸段數量或增大軸承剛度可以降低直升機機尾傳動系統的固有頻率。文獻[9]用傳遞矩陣方法分析了直升機動力傳動系統扭轉振動以及系統的振動特性，推導了直升機動力傳動系統特有并車級和行星級齒輪傳遞矩陣模型。文獻[10]利用傳遞矩陣法分析計算了復雜分支結構的車輛動力傳遞系統扭振的固有頻率及振型。文獻[11]采用傳遞矩陣法對多軸轉子系統和齒輪嚙合的多軸傳動系統線性和非線性振動問題進行了深入研究。文獻[12]通過重新定義復值狀態向量，引入外部支撐剛度、阻尼和旋轉參考系等，改進傳統傳遞矩陣法，得到復合傳遞矩陣法(Complex Transfer Matrix)，克服了傳統方法的兩大不足。

本研究針對某型小尺寸高速內嚙合齒輪軸減速器結構及動力學特點，采用傳遞矩陣法將其結構離散化，建立了系統的集總參數模型(軸盤模型)，分析計算了系統固有頻率和各階主振型，討論了其振動特性。

1　高速內嚙合齒輪軸減速器

某燃氣渦輪-泵動力裝置地面試驗系統主要由中頻電機、超越離合器、渦輪、減速器、液壓油泵等組成，其內部結構如圖1所示。高速內嚙合齒輪軸減速器是該燃氣渦輪-泵動力系統的核心部分。

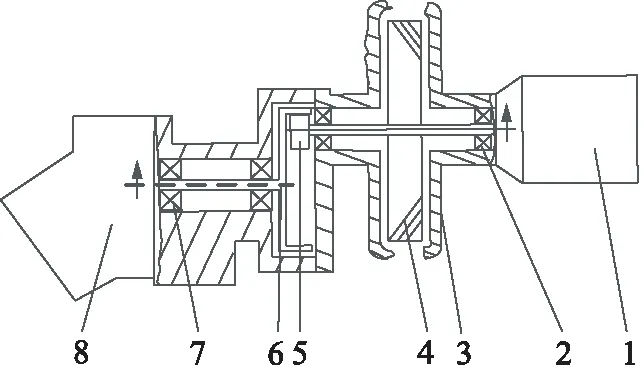
1.中頻電機　2、7.軸承　3.殼體　4.燃氣渦輪　5.外齒輪軸　6.內齒輪軸　8.液壓缸圖1　渦輪動力裝置的內部結構示意圖

該動力裝置地面試驗時，中頻電機驅動外齒輪軸提供動力，中頻電機的穩定輸出轉速為15000 r/min。動力裝置經由齒輪傳動減速后，驅動柱塞軸向柱塞液壓泵旋轉，輸出增壓油液，為電液伺服機構提供工作介質。

如圖1，該結構齒輪傳動采用內嚙合方案，動力裝置外輪廓尺寸為202 mm×150 mm×150 mm，體積小，結構緊湊。齒輪軸減速器是該型電液伺服系統的重要組成部分，結構為一級齒輪傳動，嚙合形式為內嚙合，齒輪形式為普通圓柱齒輪。

2　扭轉振動傳遞矩陣模型

先做如下假設：將內、外齒輪等效為均質圓盤； 不計入齒輪嚙合變形；假設基座對殼體的支承剛度足夠大，軸承對齒輪軸的支承剛度足夠大，內外齒輪軸的質心無橫向位移，無彎曲變形。則兩個齒輪軸只有繞中心軸線旋轉的自由度。

在假設條件下對系統做離散化：

將內嚙合齒輪傳動結構簡化為無質量的梁上帶有若干集中質量的扭轉振動系統——軸盤系統。把減速器結構中的渦輪、外齒輪和內齒輪處理為集中質量的剛體圓盤，各集中質量間的軸段簡化為無質量扭轉彈簧[13]。把傳動系統按鏈狀結構，劃分為一系列單元(一個典型單元包括一個無質量的軸段和一個作為剛體考慮的圓盤)。

在不影響計算的情況下，約定各截面上的轉角θ和扭矩M都為正值。

圖2所示為內嚙合齒輪軸傳動系統的軸盤扭振模型。

圖2　內嚙合減速器的軸盤扭振模型

圖3所示為軸、盤兩端的受力情況。

圖3　等效軸段和圓盤的受力情況示意

將任一截面上的轉角及扭矩排成列向量Z，則：

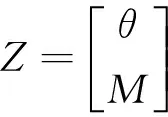
(1)

(2)

其中場傳遞矩陣:

(3)

同理，由圓盤的運動微分方程，寫出傳遞關系:

(4)

其中點傳遞矩陣:

(5)

有式(2)、式(4)得到第i單元的傳遞矩陣Hi：

(6)

依據上述定義列出相鄰狀態向量間的傳遞關系：

(7)

(8)

(9)

(10)

(11)

(12)

得出系統最左端與最右端的狀態向量之間的傳遞關系為：

(13)

記總傳遞矩陣為H，則：

(14)

3　軸盤模型解算分析

3.1　模型解算

作為ω函數的傳遞矩陣已經滿足了各個單元的運動微分方程，若試算出同時還能滿足邊界條件的ω值，則該值即為系統的某一階固有頻率。

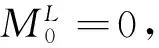
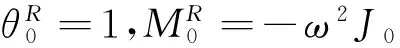
表1　扭轉振動參數表

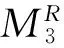
ω4J0J1-k1ω2(J1+J0)]/4k1k2+(k3-ω2J3)·

(4ω4J0J2-4k1ω2J2)/k1k3+(k3-ω2J3)·

(k2-ω2J2)[16ω4J0J1A-16ω2k1J1A+

ω4J0J1-k1ω2(J1+J0)]/4k1k2k3

(16)

圖4　余扭矩變化曲線

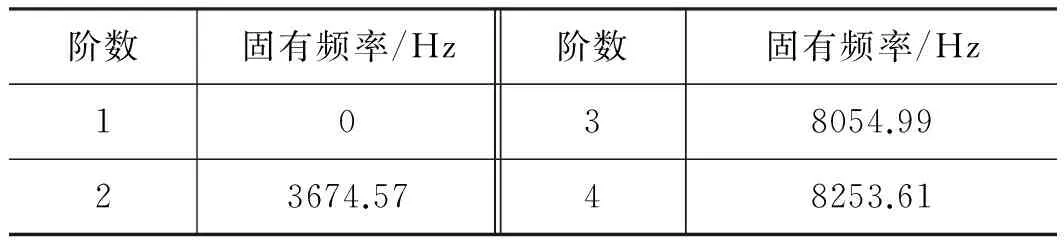
表2　扭轉振動固有頻率

表3　各主振型計算值

系統各階主振型如圖5所示。

3.2　結果分析

動力裝置的兩種驅動方式，其激勵源特性如表4所示。可以看到，當動力裝置由中頻電機驅動時，減速器嚙合頻率稍大于系統扭轉振動的2階固有頻率。燃氣渦輪驅動時，嚙合頻率稍大于系統3階、4階固有頻率。

圖5　扭轉振動各階主振型

轉速r·min-1轉頻Hz嚙合頻率/Hz對比固有頻率/Hz中頻電機驅動1500025040003674.57燃氣渦輪驅動40000667106728054.99/8253.61

模型的解析結果與地面實驗時的情形吻合，如圖6所示，當中頻電機轉速接近13800 r/min時(嚙合頻率3680 Hz)，系統振動加劇，轉速繼續提高，達到15000 r/min時(嚙合頻率4000 Hz)，稍趨平穩。

圖6　地面試驗振動頻域圖

4　結論

燃氣渦輪-泵動力裝置地面試驗系統在高速驅動時發生劇烈諧振，為找到諧振原因，本研究應用傳遞矩陣法對該系統進行了扭轉振動的動力學分析，建立了內嚙合傳動系統的軸盤模型，并進行了模型解析，得到結論如下：

(1) 分析了內嚙合齒輪軸的振動力學特性，計算了系統的各階固有頻率和主振型，為以振動信號分析為基礎的故障診斷提供了支撐；

(2) 軸盤模型解析結果得到了系統扭振固有頻率和主振型，解釋了地面試驗時，電機高速旋轉接近最高轉速過程中， 系統劇烈諧振的原因。當燃氣渦輪驅動

減速裝置動力輸出時，也應使燃氣渦輪轉速盡量迅速遠離共振區域(系統3階、4階固有頻率范圍，即8054.99～8253.61 Hz)；

(4) 不計入系統中阻尼影響時，傳遞矩陣法只需要對一些階次較低的聯系矩陣階乘運算，數值求解較為簡單，計算工作量不大。

參考文獻：

[1]毛振中. 某型直升機主減系統振動特性與控制穩定性[D].北京：北京航空航天大學, 2008.

[2]Sankar S. On the Torsional Vibration of Branched Systems Using Extended Transfer Matrix Method[J]. Journal of Mechanical Design, 1979, 101(4): 546-553.

[3]Wu J S, Chen C G. Torsional Vibration Analysis of Gear Branched Systems by Finite Element Method [J]. Journal of Sound and Vibration, 2001, 1(240):159-182.

[4]Thomson W T. Theory of Vibration with Applications[M]. Prentice-Hall, Englewood Cliffs, New Jersey,1981.

[5]Hsieh S, Chen J, Lee A. A Modified Transfer Matrix Method for the Coupling Lateral and Torsional Vibrations of Symmetric Rotor-bearing Systems[J]. Journal of Sound and Vibration,2006,289(1-2):294-333.

[6]鄧曉曉,張保成. 內燃機軸系扭轉振動綜述[J]. 研究與開發, 2012,(1):76-82.

[7]Xunwen S,Shaoping W,Dongmei Z.Vibration Analysis and Experiment of the Helicopter Rotor Test Stand Transmission[C]// Fluid Power and Mechatronics (FPM), 2011 International Conference on Fluid Power and Mechatronics.Beijing： IEEE ,2011: 202-206.

[8]朱自冰，朱如鵬，鮑和云，等.剛度對直升機尾傳動系統彎曲振動固有頻率影響的分析[J].航空動力學報，2009,24(1)：176-180.

[9]王建軍，毛振中，卿立偉，等.直升機動力傳動系統扭轉振動整體傳遞矩陣分析[J].航空動力學報，2008,23(10)：1805-1812.

[10]馮棟梁,魏來生.傳遞矩陣法在動力傳動系統扭振分析中的應用[J].車輛與動力技術, 2010(1):41-45.

[11]Choi S T, Mau S Y. Dynamic Analysis of Geared Rotor-bearing Systems by the Transfer Matrix Method [J]. Journal of Mechanical Design, 2001, 123(4):563-568.

[12]Varney P, Green I. Rotor Dynamic Analysis Using the Complex Transfer Matrix[C]//ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Chicago, IL, USA, 2012: 237-246.

[13]倪振華.振動力學[M].西安：西安交通大學出版社,1989.