軸向柱塞泵主軸及缸體旋轉組件臨界轉速分析

， 　， ， ， 孔祥

(1.燕山大學 河北省重型機械流體動力傳輸與控制實驗室， 河北 秦皇島　066004；2. 燕山大學 先進鍛壓成形技術與科學教育部重點實驗室， 河北 秦皇島　066004；3.燕山大學 機械工程學院， 河北 秦皇島　066004)

引言

軸向柱塞泵是液壓系統振動產生的主要根源之一，50%以上的液壓系統振動是由軸向柱塞泵工作產生的[1]。而且，隨著軸向柱塞泵向高壓、高速方向發展[2]，軸向柱塞泵的振動模態更為豐富，振動幅值更為寬泛[3]。機械運動是軸向柱塞泵振動產生的主要因素之一，尤其是其轉子系統的高速旋轉運動，更會在泵體內產生復雜振動。

軸向柱塞泵的轉子系統是其核心部件，轉子系統的旋轉運動使軸向柱塞泵完成機械能向液壓能的轉化。轉子系統的不平穩運動是引起軸向柱塞泵機械振動的主要原因。對于旋轉機械而言，轉子系統的設計必然會考慮動平衡問題。研究發現，當轉子系統從低速開始增加旋轉速度到某個轉速時，轉軸會發生劇烈振動，該轉速稱為“臨界轉速”。計算轉子臨界轉速是轉子系統動力學的重要研究內容之一[4]。轉子系統的臨界轉速同轉子系統結構特點、參數，如轉子系統的軸頸比、質量分布、約束條件、材料剛度等有直接關系[5-8]。

提高軸向柱塞泵轉速，使其服務于功重比要求更高的液壓控制系統，已經成為必然趨勢，例如，由于航空發動機轉速較高(某型航空發動機地面試車最大轉速達到了16000 r/min)，因此設計與其相匹配的高壓高速軸向柱塞泵是后續工作的前提[9]。國外很多航空液壓元件公司生產的電靜液驅動作動器動力源一般都是高速電機直接驅動液壓泵的方式，電機轉速非常高，很多可達到每分鐘上萬轉，因此要求軸向柱塞泵也有相應的轉速[10]。據最新調研發現，我國某公司生產的一種型號的電靜液驅動作動器使用的軸向柱塞泵在實驗室的理想環境下，轉速只能達到9000 r/min； 而該公司生產的排量稍大的一種軸向柱塞泵在研制過程中發現，當其轉速達到7500 r/min時，會發生明顯諧振。

轉子動力學是軸向柱塞泵臨界轉速研究的理論基礎[11]。傳遞矩陣法和有限元法是分析復雜轉子系統轉子動力學特性的主要手段。20世紀50年代，傳遞矩陣法被應用于轉子系統的分析和臨界轉速計算，直到現在仍然是轉子動力學的主要分析手段之一。其優點是矩陣階數不隨系統自由度增大而增加，因而編程簡單、內存用量小、運算速度快；缺點是不便于分析周圍結構對轉子動力學特性的影響。有限元法特別適用于由轉子和周圍結構組成的轉子系統分析，但會增大模型自由度，大量占用計算機資源。隨著計算機水平的提高，有限元法得到了更為廣泛的應用[12]。

本研究針對某斜盤式軸向柱塞泵轉子系統進行研究，通過傳遞矩陣法及有限元法分析其臨界轉速，并提出提高臨界轉速的有效方法，為軸向柱塞泵轉子系統轉子動力學分析提供基礎。

1　軸向柱塞泵轉子系統集總參數建模

傳遞矩陣法要求把轉子簡化為具有若干個集總質量的多自由度系統，利用集總參數法獲得集總參數模型[13]。

圖1所示為本研究的軸向柱塞泵轉子系統三維模型，由于軸向柱塞泵缸體與轉軸之間為過盈連接，故在分析時，將缸體與轉軸視為一體，并忽略配流盤及柱塞的作用。將簡化后所得到的轉子系統向23個結點集總，如圖2所示，其中結點9、11、23為軸承所在位置。

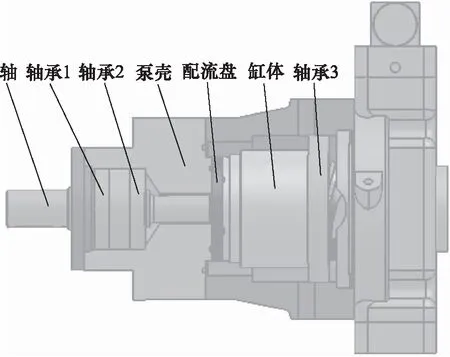
圖1　軸向柱塞泵轉子系統

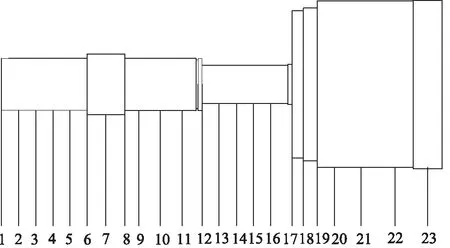
圖2　軸向柱塞泵轉子系統結點分布圖

所劃分結點之間的軸段包含等截面軸段和不等截面軸段，針對等截面軸段，其質量及轉動慣量的集總公式如式(1)～式(3)所示：

(1)

(2)

(3)

其中,Mi、Jpi、Jdi分別為簡化到結點i處的質量、極轉動慣量和直徑轉動慣量。m、jp、jd和l分別為對應軸段單位長的質量、極轉動慣量、直徑轉動慣量和長度。(ml)i即mili，其余表述方法與此相同。

不等截面情況下的集總公式為：

(4)

(5)

(6)

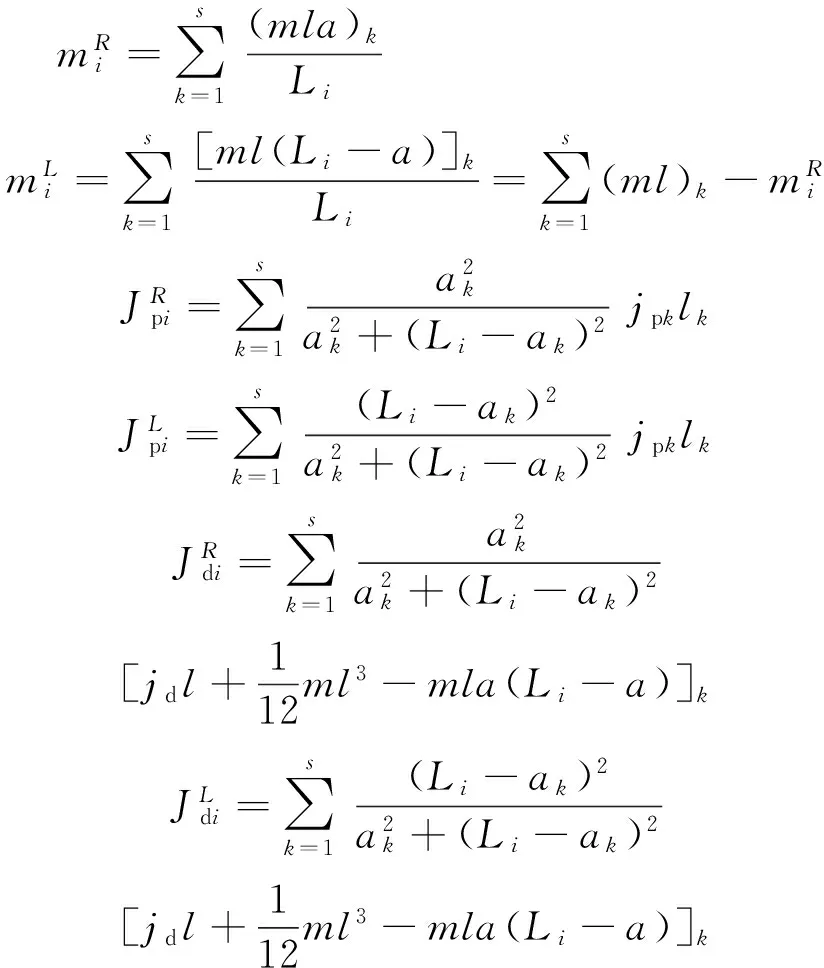
其中,mk—— 各軸段單位長的質量

jpk—— 極轉動慣量

jdk—— 直徑轉動慣量

lk—— 軸段長度

ak—— 相應質心到左端面的距離

Li—— 全長

s—— 第i個軸段的不同尺寸截面個數

各結點的等效抗彎剛度(EI)i可按純彎時兩段截面的相對轉角不變來求得，即:

(7)

測量轉子系統的基本參數，并查閱相應的材料密度ρ=7850 kg/m3、 彈性模量E=205 GPa， 進而根據式(1)～式(7)可以得到軸向柱塞泵轉子系統集總參數模型中的參數如表1所示。

軸向柱塞泵的支撐軸承為滾動軸承，忽略阻尼影響，可以將其簡化為彈性支承，考慮軸向柱塞泵軸承實際工況，本研究取支撐剛度K為2×106N·m。得到轉子系統集總參數模型如圖3所示。

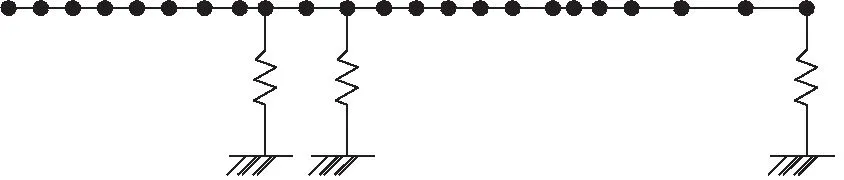
圖3　轉子系統集總參數模型

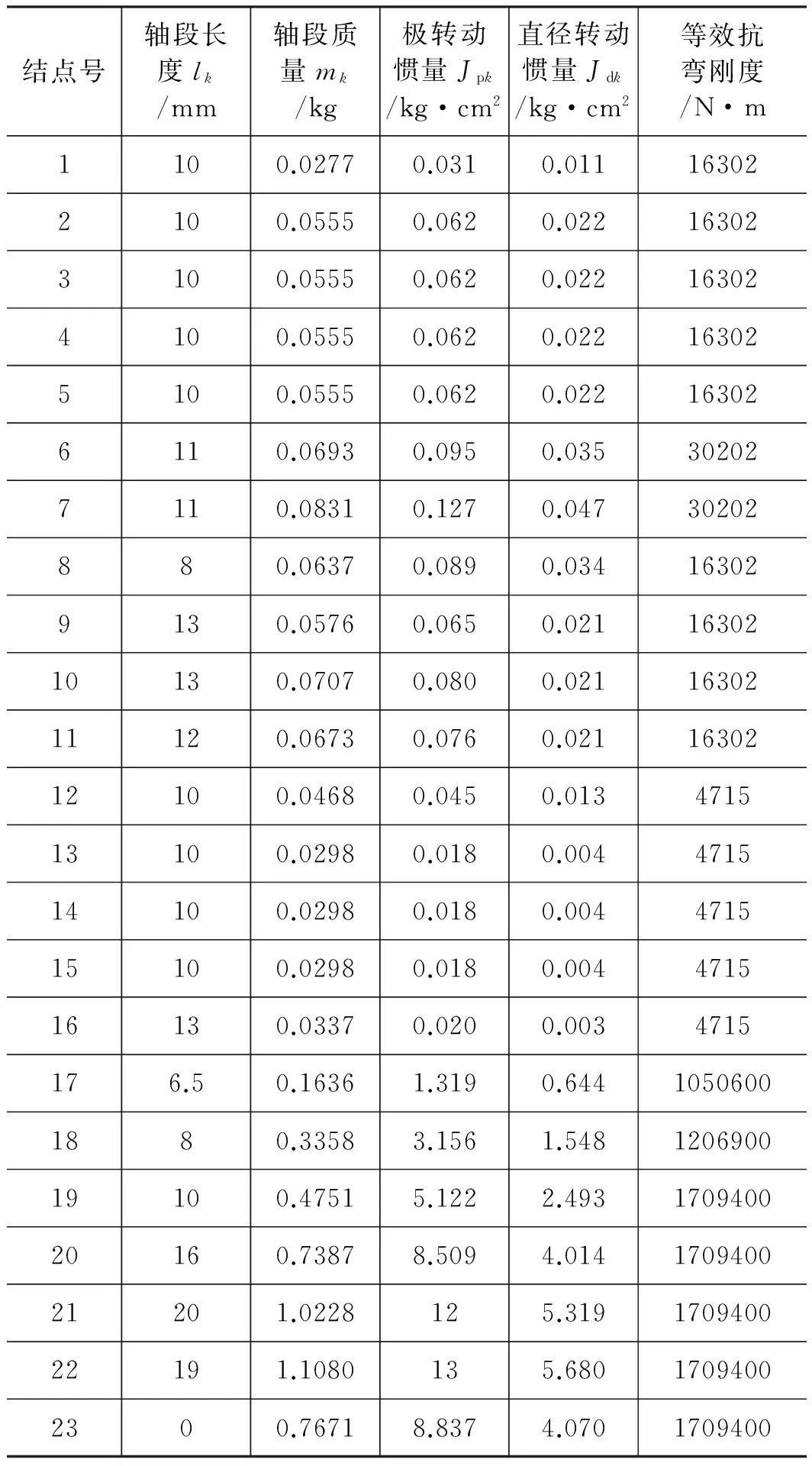
結點號軸段長度lk/mm軸段質量mk/kg極轉動慣量Jpk/kg·cm2直徑轉動慣量Jdk/kg·cm2等效抗彎剛度/N·m1100.02770.0310.011163022100.05550.0620.022163023100.05550.0620.022163024100.05550.0620.022163025100.05550.0620.022163026110.06930.0950.035302027110.08310.1270.04730202880.06370.0890.034163029130.05760.0650.0211630210130.07070.0800.0211630211120.06730.0760.0211630212100.04680.0450.013471513100.02980.0180.004471514100.02980.0180.004471515100.02980.0180.004471516130.03370.0200.0034715176.50.16361.3190.64410506001880.33583.1561.548120690019100.47515.1222.493170940020160.73878.5094.014170940021201.0228125.319170940022191.1080135.68017094002300.76718.8374.0701709400

2　軸向柱塞泵轉子系統集總參數數學模型

2.1　傳遞矩陣法

傳遞矩陣法是把轉子系統根據結構分為若干個典型部件，利用連續條件建立這些部件兩端截面狀態向量間的力學傳遞模型，并對滿足邊界條件的渦動頻率搜索，得出轉子系統的各階臨界轉速[4]。對于編號為i和i+1的兩個相鄰部件，其狀態向量之間的關系為：

(8)

其中，Zi、Zi+1分別為兩個截面的狀態向量;yi、θi、Mi及Qi分別為截面i處的撓度、斜率、彎矩和剪力；[T]i為相鄰兩部件間的傳遞矩陣。

對劃分為n個部件的系統，由式(8)可得：

Z2=[T]1Z1

Z3=[T]2Z2=[T]2[T]1Z1

Zi=[T]i-1[T]i-2[T]i-3…[T]1Z1=Ai-1Z1(9)

其中，Ai-1=[T]i-1[T]I-2…[T]1

式(9)表達出各截面狀態向量中的元素都可以表為起始截面狀態向量中各元素的線性組合。因此，當起始截面的狀態向量已知時，通過式(9)的遞推關系，就可求得各截面的狀態向量。

圖4所示為剛性薄圓盤剛性圓盤及和無質量等截面彈性軸段組成的兩個相鄰部件。

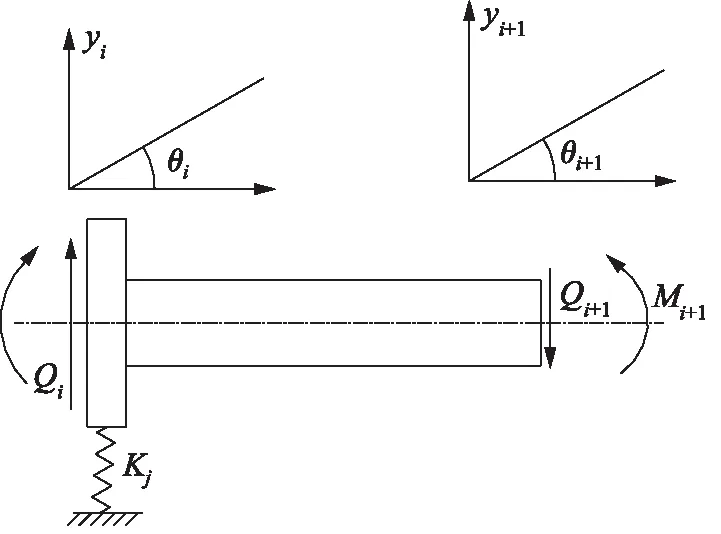
圖4　圓盤與軸段組合結構

對于圖4的模型，由邊界條件有：

M1=0;Q1=0

(10)

因此對于任一截面i，由式(9)有：

(11)

則對于末端截面由式(11)可得:

(12)

末端截面的邊界條件為:

Mn+1=0;Qn+1=0

(13)

令:

(14)

稱Δ(ω2)為剩余量。當邊界條件滿足時，該齊次式有解的條件是Δ(ω2)為零，即:

Δ(ω2)=0

(15)

滿足式(15)的ω即為臨界角速度，可以通過自編程序求解。其大小與轉子系統的支撐剛度和質量有直接關系。

2.2　傳遞矩陣求解

采用MATLAB軟件，根據傳遞矩陣求解方法，編寫M文件，其主要程序如下:

while dw1*dw2>=0 %循環條件

T=1;

for i=23:-1:1

T=T*[1+l(i)^3*(m(i)*w^2-k(i))/(6*EI(i)),l(i)+l(i)^2*(Jp(i)-Jd(i))*w^2/(2*EI(i)),l(i)^2/(2*EI(i)),l(i)^3/(6*EI(i));l(i)^2*(m(i)*w^2-k(i))/(2*EI(i)),1+l(i)*(Jp(i)-Jd(i))*w^2/EI(i),l(i)/EI(i),l(i)^2/(2*EI(i));l(i)*(m(i)*w^2-k(i)),(Jp(i)-Jd(i))*w^2,1,l(i);m(i)*w^2-k(i),0,0,1];

end

dw1=T(3,1)*T(4,2)-T(4,1)*T(3,2);

求解dw2的程序與上述程序類似，此處不再贅述。求得的一階臨界轉速為7993.2 r/min。

3　軸向柱塞泵轉子系統臨界轉速有限元分析

3.1　有限元模型建立

結合圖1，建立軸向柱塞泵轉子系統有限元模型，并根據以下原則進行簡化。

(1) 忽略缸體與轉軸之間的相互作用，而且二者密度相同，則將二者看做一個整體；

(2) 忽略軸承油膜影響，將其簡化為彈性支撐；

(3) 認為軸承只具有徑向剛度，且剛度值為定值，則將其進一步簡化為彈簧單元；

在SolidWorks軟件中進行三維建模，將模型倒入ANSYS中，設置材料屬性，進入Model模塊采用四面體網格進行網格劃分，單元尺寸設置為4 mm，共有154127個節點，107318個單元。如圖5所示。

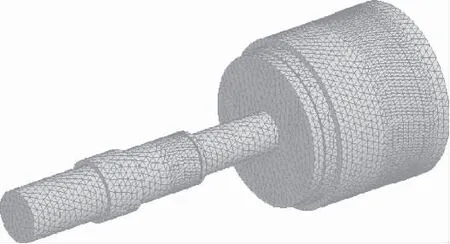
圖5　軸向柱塞泵轉子系統有限元網格模型

3.2　接觸與約束條件設置

有限元模型中約束條件的設置對數值模態分析結果影響很大[14-16]。結合軸向柱塞泵的實際工作情況，在軸承安裝軸段的軸肩處(圖6中A所指示區域)設置位移約束，以約束軸段的軸向位移，并在軸承結點位置添加彈簧接觸。為獲得轉子系統的臨界轉速，還需要對其施加一系列轉速(圖6中箭頭指向為旋轉方向)，本次分析，轉速范圍為2000～11000 r/min，步長為1000 r/min。模型的約束條件設置如圖6所示。

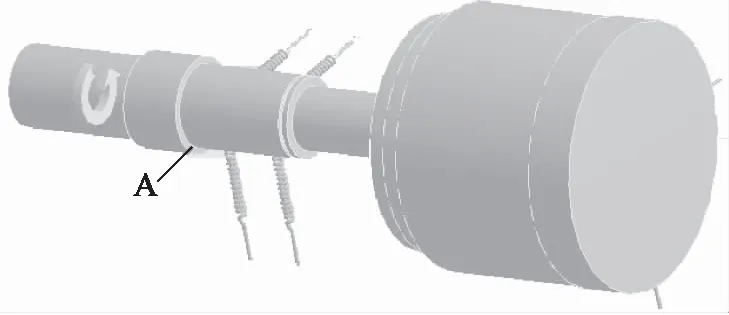
圖6　約束條件設置

3.3　泵轉子系統臨界轉速分析

實際轉子旋轉過程中，由于陀螺力矩的存在，使得轉子的固有頻率會隨著轉速而發生變化。坎貝爾圖是瞬態信號分析中最基本的方法，從中可以得到整個轉速范圍內轉子振動全部頻率分量的變化特征。其橫坐標為轉速，縱坐標為頻率，根據臨界轉速的定義，在坎貝爾圖中畫一條從原點出發的等頻線與各階固有頻率的交點即為臨界轉速。由于轉子的臨界轉速一般是指同步正向渦動時的臨界轉速，因此只取等頻線與正進動頻率的交點。求得的坎貝爾圖如圖7所示。

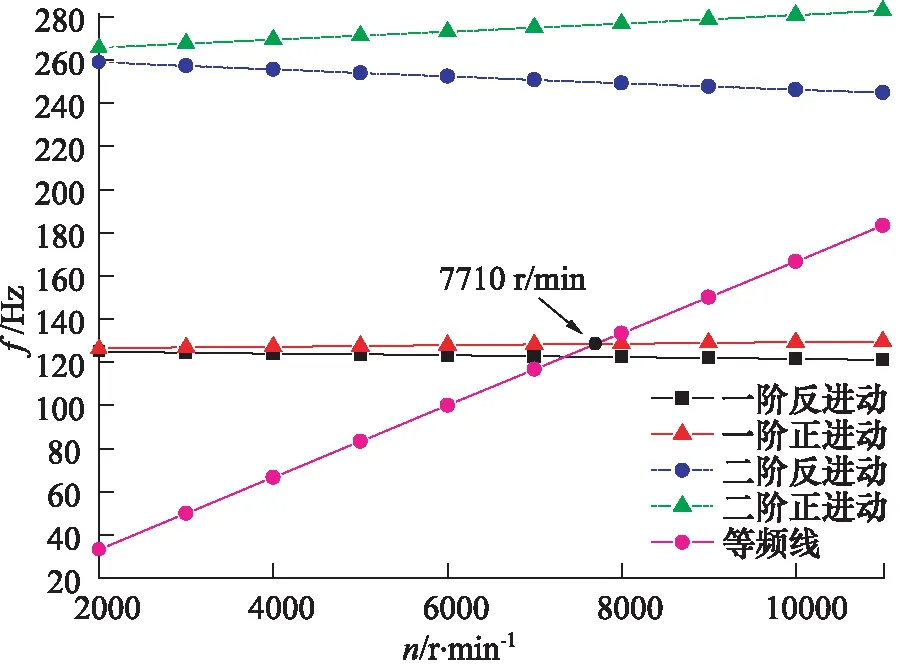
圖7　轉子系統坎貝爾圖

得到轉子系統的一階臨界轉速為7710 r/min，對比MATLAB的分析結果，其相對誤差為3.5%，誤差很小，證實了有限元解法的正確性。

所求得的正進動時前兩階振型如圖8所示。

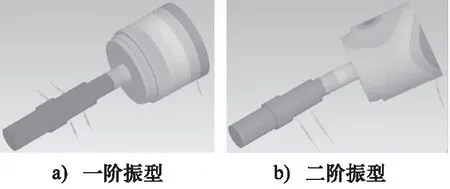
圖8　泵轉子振型

從振型圖中可以看出，一階振型中缸體端部的位移最大，二階振型中軸輸入端的位移最大，出現此種振型的原因是由于軸承剛度較低。因此可以通過增加軸承剛度來提高轉子的臨界轉速，將缸體位置的彈簧剛度設置為5×106N·m，得到坎貝爾圖如圖9所示。

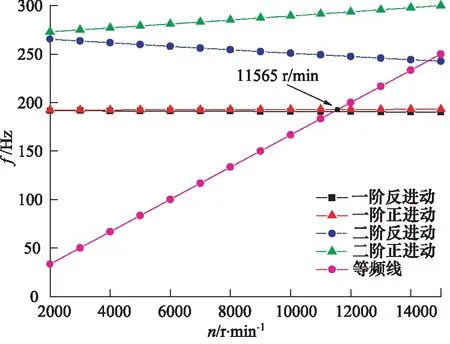
圖9　增加缸體位置彈簧剛度后的坎貝爾圖

可以看出，增加彈簧剛度后，臨界轉速提高了50%，說明軸承剛度對臨界轉速有很大影響。因此，提高軸承剛度是提高臨界轉速的有效方法。此外，由于缸體質量占據了整個轉子系統的很大比重，造成轉子系統質量分布不均勻。將缸體直徑減小2 mm，彈簧剛度與初次分析相同，再次求得其坎貝爾圖如圖10所示。在減小缸體直徑后臨界轉速提高了195 r/min，這是因為缸體直徑減小后，其質量減小，所占轉子系統比重降低，軸向質量分布更為均勻，因此提高了臨界轉速。

從以上分析可以看出，軸向柱塞泵轉子系統的支撐剛度提高及缸體質量降低均能夠提高其臨界轉速。

4　結論

針對軸向柱塞泵高速化發展的趨勢，采用轉速傳遞矩陣及有限元方法得到了轉子系統第一階臨界轉速。并得出如下結論：

(1) 軸向柱塞泵轉子系統的軸承剛度對臨界轉速有很大影響，提高軸承剛度是提高臨界轉速的有效方法之一；

(2) 軸向柱塞泵轉子系統軸向質量分布對臨界轉

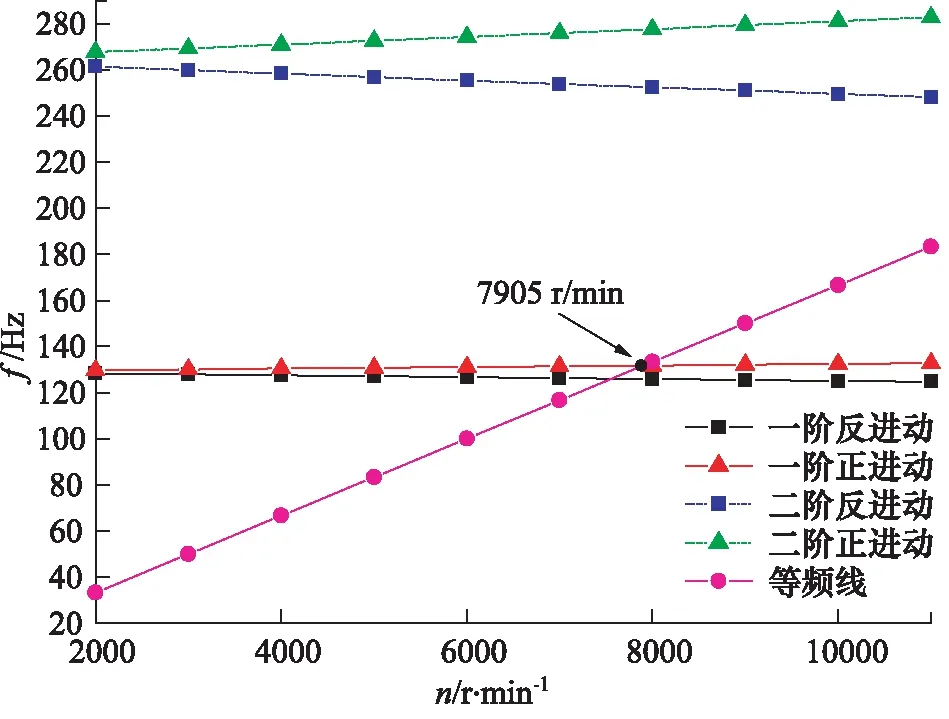
圖10　減小缸體直徑后的坎貝爾圖

速也有很大影響，缸體直徑減小，軸向質量分布更加均勻時，能夠提高臨界轉速。

參考文獻：

[1]王占林.飛機高壓液壓能源系統[M].北京:北京航空航天大學出版社,2004.

[2]徐兵,陳媛,張軍輝.軸向柱塞泵減振降噪技術研究現狀及進展[J].液壓與氣動,2014，(3):1-10.

[3]權凌霄,駱洪亮,張晉. 斜軸式軸向柱塞泵殼體結構振動諧響應分析[J].液壓與氣動,2014，(5):33-39.

[4]袁惠群.轉子動力學基礎[M].北京:冶金工業出版社,2013.

[5]Kyo-Nam Koo.Vibration Analysis and Critical Speeds of Polar Orthotropic Annular Disks in Rotation [J]. Composite

Struc-tures,2006,76(1):67-72.

[6]Hyun-Moo Hur,Joon-Hyuk Park.A Study on the Critical Speed of Worn Wheel Profile Using a Scale Model[J]. Journal of Mechanical Science and Technology,2009,23(10):2790-2800.

[7]Sh Hosseini-Hashemi, M Fadaee. Accurate Natural Frequencies and Critical Speeds of a Rotating Functionally Graded Moderately Thick Cylindrical Shell [J]. Interna-tional Journal of Mechanical Sciences,2013,(76):9-20.

[8]R Penteado, A F Salvador. Physiological Responses at Critical Running Speed during Continuous and Intermittent Exh-austion Tests[J]. Science & Sports, 2014,(29):99-105.

[9]雷勇.航空高壓高速液壓柱塞泵的設計研究[D].貴州:貴州大學,2006.

[10]習仁國,劉衛國,等.電靜液作動器的建模仿真與試驗研究[J].機床與液壓,2013,41(19):40-44.

[11]成曉偉.離心泵轉子部件臨界轉速的分析與計算[D].蘭州:蘭州理工大學,2009.

[12]關棟,楊小輝.高速永磁電機轉子系統臨界轉速仿真研究[J].振動與沖擊,2013,(12):5-7.

[13]田野,孫巖樺.不同支撐和轉子裝配方式的高速電機臨界轉速分析[J].振動與沖擊,2013,(8):24-30.

[14]丁欣碩,凌桂龍.ANSYS Workbench 14.5有限元分析案例詳解[M].北京:清華大學出版社,2014.

[15]李超,劉延峰.基于混合模型的轉子臨界轉速計算[J].振動與沖擊,2010,(11):245-248.

[16]梅若愚,傅波,付玄,等.基于ANSYS Workbench的分體式壓力矯直機主機機體結構優化[J].液壓與氣動,2012,(3):66-68.

廣告刊戶索引

北京華德液壓工業集團有限責任公司

封面

上海敏泰液壓股份有限公司

封二

寧波星箭航天機械有限公司

廣1

新鄉市平菲液壓有限公司

廣2

南京訊聯液壓件有限公司

廣3

寧波華液機器制造有限公司

廣4

哈威油液壓技術(上海)有限公司

廣5

江蘇恒源液壓有限公司

廣6

頗爾過濾器(北京)有限公司

廣7

黎明液壓有限公司

廣8

寧波高新協力機電液有限公司

廣9

徐州車氏密封有限公司

廣10

江蘇省鹽城市馬溝液壓件廠

廣11

德州市天元液壓機具有限公司

廣12

德州市巨力液壓機具有限責任公司

廣13

蕪湖市銀鴻液壓件有限公司

廣14

2016期刊聯合征訂

廣15

阿托斯液壓產品(上海)有限公司

廣16

黎明液壓有限公司

廣17

2016中國機械工程學會期刊聯合

征訂

廣18

深圳市特力得流體系統有限公司

廣19

北京四達合道液壓技術有限公司

封三

九江七所精密機電科技有限公司

封底