基于稀疏重建的信號DOA估計

任肖麗，王 驥，萬 群

1.廣東海洋大學 信息學院，廣東 湛江 524088

2.電子科技大學 電子工程學院，成都 611731

1 引言

源定位是信號處理領域的主要目的之一，利用傳感器陣列可以將其轉換成DOA估計。在已有的DOA估計方法中，信號子空間概念由于其超分辨性能已經成為一種主導技術，如MUSIC[1]。近幾年，壓縮感知（Compressed Sensing，CS）理論及其應用[2-4]成為了研究熱點。CS提出了許多方法來解決稀疏重建問題，其中有兩種主要算法方法：基追蹤[5]（Basis Pursuit，BP）算法依賴于一個優化問題，可以通過線性規劃求解，具有穩定性并能準確重建信號，但是需要大量的計算；貪婪算法[6-7]具有低復雜度和較快的速度，但是缺乏穩定性和一致性保證。通過利用稀疏性，出現了許多方法[8-19]，可以提供比MUSIC更好的分辨性能。本文基于?1-SVD方法[10]，將DOA估計問題轉化成稀疏信號重建問題并且利用CS方法求解。?1-SVD方法具有極好的超分辨性能和信號相關的穩健性。

線性陣列是多陣元天線的一種重要形式，在通信和射電天文學中起著重要的作用。1968年，Moffet在文獻[10]中提出了最小冗余線（MRLA），能以較少數的陣元獲得較大陣列孔徑，是一種有效的陣列排布方法，陣列孔徑和DOA分辨率、可估計的信號源數成正比，即陣列孔徑越大估計性能更好。許多學者已經對MRLA進行進一步的研究[11]，充分利用了MRLA的這一結構特征。均勻線陣（ULA）是冗余的，是因為不同陣元對可以得到相同的共軛循環相關函數值。同樣，不同陣列傳感器分布可以獲得相同的共軛循環相關函數值，冗余度隨陣元數的增大而增大。因此，基于MRLA的結構特點，本文將MRLA與?1-SVD方法相結合來估計信號的DOAs。

2 問題描述

考慮到N個具有相同中心頻率的窄帶信號源從不同方向θi(i=1，2，…，N)入射到M陣元均勻直線陣上，陣元間隔x～1(t)，λ為載波波長，M×1陣列接收信號 y(t)表示為：

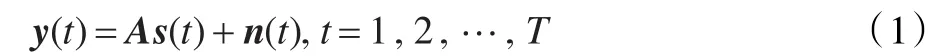
可以把欠定方程（1）中s(t)恢復問題轉化CS應用的稀疏信號重建問題。s(t)可以通過?1最小化恢復得到：

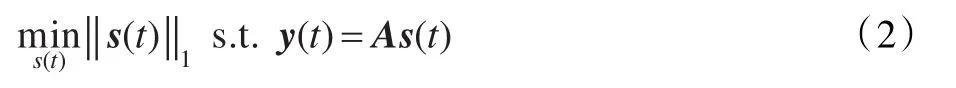
式（1）的矩陣形式可以表示為：

其中，M×T矩陣 Y=[y(1)，y(2)，…，y(T)]和M×T矩陣N=[n(t)，…，n(T)]，T表示快拍個數，信號向量 S=[s(1)，s(2)，…，s(T)]∈N×T。

2.1 ?1-SVD方法

對于窄帶信號源而言，當不相關信號和相干信號同時存在時，多測量數據為：

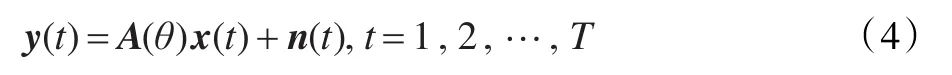
其中，A(θ)=[a(θ1)，a(θ2)，…，a(θN)]未知，在稀疏假設下，N是小的，文獻[10]把DOA估計問題轉化成一個稀疏信號重建問題，構建字典，Kmax(N，M)，假設{θ1，θ2，…，θN}令si(t)=，Y=AS+N ，Y=[y(1)，y(2)，…，y(T)]。

對矩陣Y奇異值分解（SVD）Y=UΛVH，令YSV=UΛDK=YVDK，其中DK=[IK0]′，IK為K×K單位矩陣，0是K×(T-K)零矩陣，令 SSV=SVDK，NSV=NVDK，為了滿足YSV=ASSV+NSV，逐列考慮此方程有：

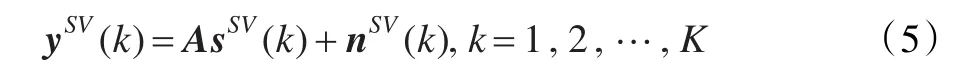
?1-SVD方法可概括成如下三步：做奇異值分解Y=UΛVH；取YV的前N列，記為YSV，M×N；求解下面的優化問題：

其中，SSV∈K×N為 SV的前N列，K×1維 SC定義為SSV的2范數，是估計的稀疏譜，β是給定的調整參數。

?1-SVD方法的主要優點是具有很好的超分辨性能和信號相關穩健性，缺點主要是需要已知信號源個數且復雜度隨其成比例增加，當陣元數為M，各信源相距不太近時，?1-SVD方法能分辨出的信源個數最多是M-1。

2.2 最小冗余線陣（MRLA）

對于ULA，x(t)的相關矩陣為：

其中，E(·)、(·)H和 (·)*分別表示期望、轉置和共軛算子。r(m)，m=0，1，…，M-1是隨機過程 x(t)的相關函數。由式（1）和（8）可得：

其中，RS=E[s(t)sH(t)]，當信號源相互獨立或不相關時，顯然 R是Toeplitz矩陣，根據Toeplitz矩陣結構特點，只要已知R第一行，就可以準確重構整個矩陣。

式（8）表明，對于具有M陣元的ULA，在M2個相關函數中只有M個獨立的相關函數。因此，ULA輸出相關矩陣是一個冗余的Toeplitz矩陣，減少線性陣列冗余的常用方法是采用非均勻線陣。事實上，不同的陣元分布可以獲得與ULA相同的相關函數，冗余度隨著陣元數增加而增加。設計MRLA的原則是將非均勻線陣的M陣元與ULA的P陣元等價，其中M＜P。表1為一些最小冗余線陣配置，其中{di}表示相對于參考陣元而言第i個陣元的位置[12]。

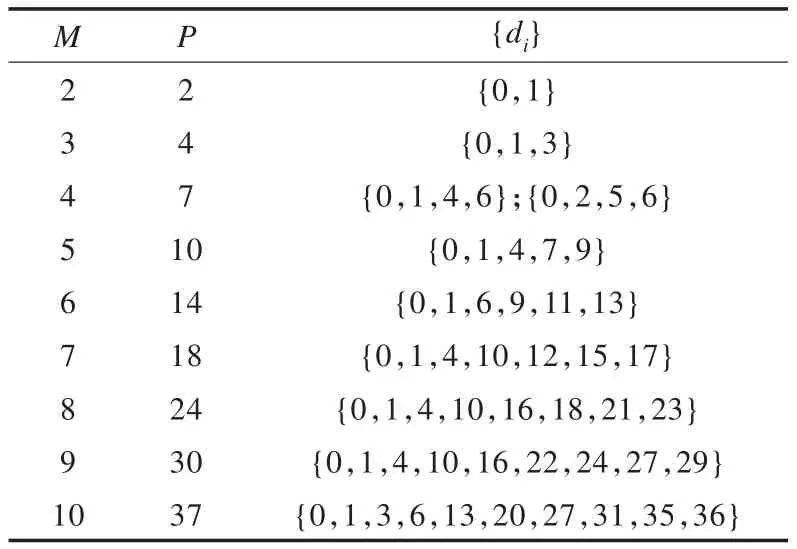
表1 一些最小冗余線陣配置

3 本文方法

假設具有M陣元的無源線性陣列，相對于參考陣元的陣元位置d1＜d2＜…＜dM，每個陣元位置di都是固定距離d的整數倍。假設一個M陣元的非均勻線陣，N個獨立的窄帶信號源，其中信號源個數N是已知的，在此，取M=4為例，設相對于參考陣元的陣元位置為d1,d2,d3,d4，且有如下取值{d1,d2,d3,d4}={0,2d,5d,6d}，d=λ/2，λ為信號載波波長，陣列接收向量X(t)=[x0(t)x2(t)x5(t)x6(t)]T可通過下式得到：

其中，t=1，2，…，T，陣列接收向量的相關矩陣為：

對矩陣R奇異值分解，保留其信號子空間US，構建字典，其中Nθ是角度采樣數，Nθ×1維向量的稀疏性對應空間譜的稀疏性，通過最小化式（12）估計DOA：

由于獨立信號的相關矩陣具有Toeplitz結構，且矩陣 R中含有r(0)，r(1)，r(2)，r(3)，r(4)，r(5)，r(6)，構造7×7的擴展矩陣：

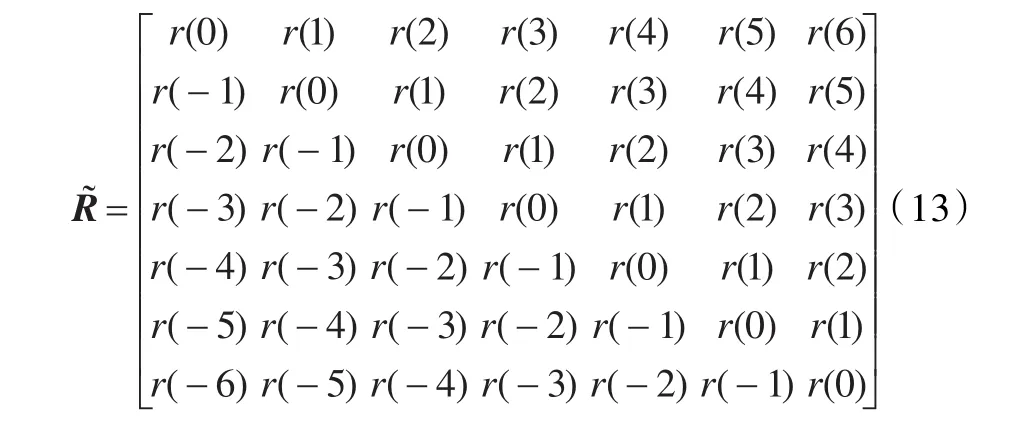
又有r(-m)=r*(m)，(m=0，1，…，6)，則通過 R 可以得到具有7陣元ULA的相關矩陣：

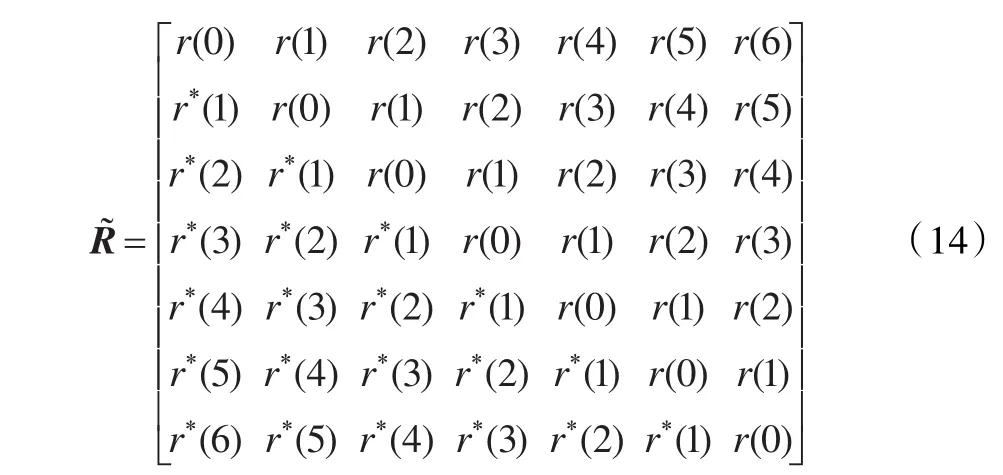
其中，DOA估計問題被看作是子空間快稀疏重建，構建超完備字典=[a(θ1)，a(θ2)，…，a(θK)]，7×K，K為角度采樣數，K＞＞N，[θ1，θ2，…，θK]為所有可能的信號采樣角度。是矩陣∈K×N的第i行，即為優化問題的解。Frobenius范數定義為，β是正則化參數。在此選取足夠高的β使的概率很小，其中。向量的稀疏性對應于稀疏譜的稀疏性。由式（15）可以得到S～的稀疏譜。本文所提方法也需要已知信源個數N。

4 仿真實驗

其中，T為快拍數。

假設所有信號源都具有相同的能量，輸入信噪比SNR為是噪聲的能量。通過500次Monte Carlo仿真得到DOA估計的均方根誤差RMSE：

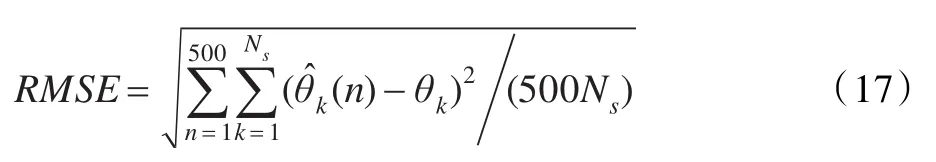
其中，()n是第n次MonteCarlo仿真中θk的估計，Ns是信號的個數，取T=1 000。

在仿真中，取M=4 ，分別來自于 [-22°，3°， 41°]和[-22°，3°，24°，41°]的獨立信號。圖1和圖2分別為基于?1-SVD方法的DOAs估計和基于本文方法的DOAs估計，顯然?1-SVD方法不能準確地估計3個和4個信號的DOAs。基于本文方法DOA估計的RMSE如圖3和圖 4 所示。當有來自于 [-45°，-22°，3°，24°，41°]的 5個獨立信號時，圖5和圖6分別表示基于本文方法的DOA估計及其RMSE。同理，當M=5，假設分別來自于 [-45°， -22°， -12°，10°，25°，48°]的6個獨立信號和[-44°， -22°， -12°，12°，26°，48°，63°]的7個獨立信號，圖7和圖9為信號的DOAs估計，圖8和圖10表示基于所提方法的RMSE。

圖1 兩種方法3個信號的DOAs估計

圖2 兩種方法4個信號的DOAs估計

圖3 本文方法3個信號DOA估計的RMSE

圖4 本文方法4個信號DOA估計的RMSE

圖5 本文方法5個信號的DOAs估計

圖6 本文方法5個信號DOA估計的RMSE

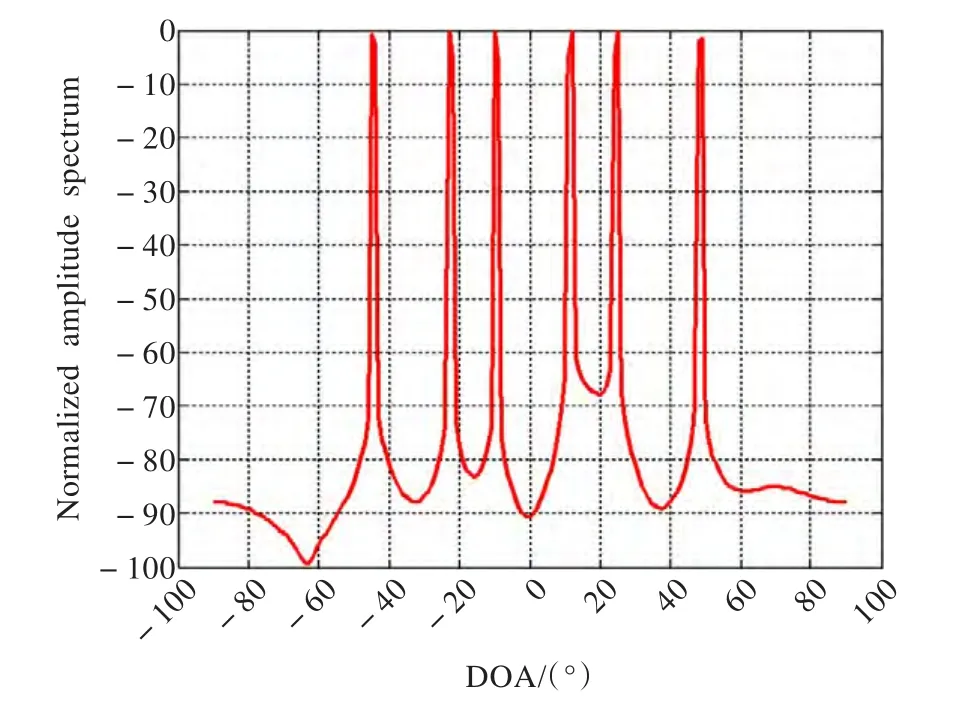
圖7 本文方法6個信號的DOAs估計

圖8 本文方法6個信號DOA估計的RMSE

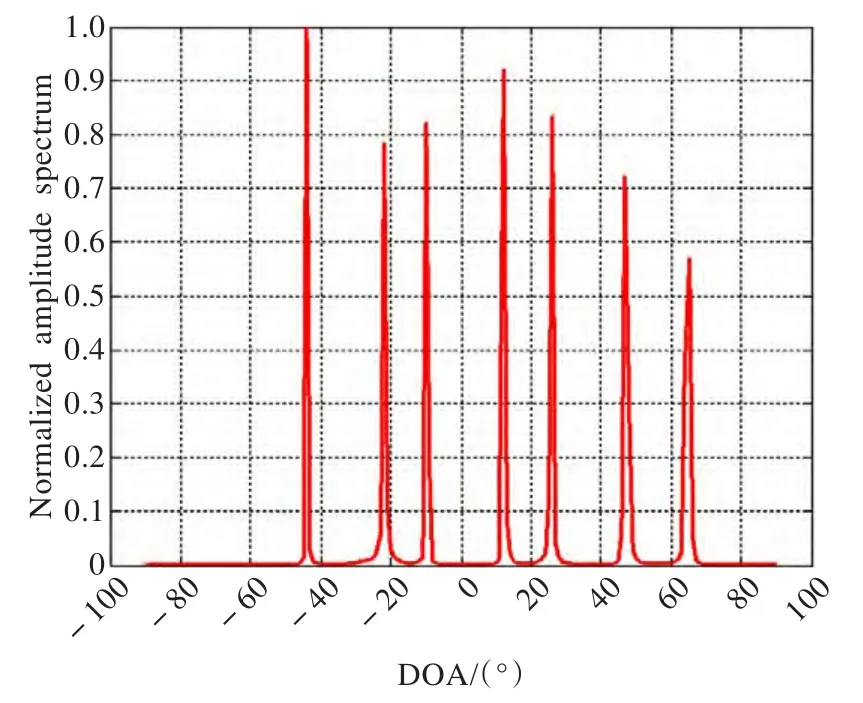
圖9 本文方法7個信號的DOAs估計

圖10 本文方法7個信號DOA估計的RMSE

仿真結果表明，對于4陣元非均勻線陣，利用本文方法在誤差允許范圍內最多可以有效估計5個獨立信源的DOAs，而?1-SVD方法不能準確估計3個及以上的信號DOA。對于5陣元非均勻線陣，利用本文方法最多可以有效估計7個獨立信源方向。值得注意的是，本文所提方法適用于獨立信號和不相關信號。同理，陣元數M可以取其他值，利用本文方法可以有效估計更多的獨立信源DOAs。

5 結論

將最小冗余線陣與?1-SVD方法相結合提出了一種新的DOA估計方法，仿真結果驗證了本文方法的有效性，其能有效估計不相關信號和獨立信號的DOA，具有信源過載能力。

[1]Schmidt R O.Multiple emitter location and signal parameter estimation[C]//Proc RADC Spectrum Estimation Workshop，Rome，NY，1979：243-258.

[2]Donoho D L.Compressed sensing[J].IEEE Trans on Information Theory，2006，52（4）：1289-1306.

[3]Candès E.Compressive sampling[C]//Proceedings of the International Congress of Mathematicians，Madrid，Spain，2006：1433-1452.

[4]Needel D.Topics in compressed sensing[D].Davis：Univ of California，2009.

[5]Chen S，Donoho D，Saunders M.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing，1999，20（1）：33-61.

[6]Pati Y C，Rezaiifar R，Krishnaprasad P S.Orthogonal matching pursuit：recursive function approximation with applications to wavelet decomposition[C]//Proceedings of the 27th Annual Asilomar Conference in Signals，Systems，and Computers，Monterey，CA，USA，1993：40-44.

[7]Tropp J.Greed is good：algorithmic results for sparse approximation[J].IEEE Trans on Inform Theory，2004，50（10）：2231-2242.

[8]Fuchs J J.On the application of global matched filter to DOA estimation with uniform circulararrays[J].IEEE Trans on Signal Process，1999，47（1）：187-200.

[9]Sacchi M D，Ulrych T J，Walker C J.Interpolation and extrapolation using a high-resolution discrete Fourier transform[J].IEEE Trans on Signal Process，1998，46（1）：31-38.

[10]Moffet A T.Minimum redundancy linear arrays[J].IEEE Trans on AP，1968，16：172-175.

[11]Gelli G，Luciano I.Minimum-redundancy linear arrays for cyclostationarity-based source location[J].IEEE Trans on SP，1997，45（10）：2605-2608.

[12]Malioutov D，Cetin M，Willsky A S.Optimal sparse representations in general overcomplete bases[C]//Proc IEEE Int Conf Acoust，Speech，Signal Process，2004.

[13]Malioutov D，Cetin M，Willsky A S.A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Trans on Signal Process，2005，53（8）：3010-3022.

[14]Zheng J，Kaveh M，Tsuji H.Sparse spectral fitting for direction of arrival and power estimation[C]//Proceeding of the 15th IEEE Workshop on Statistical Signal Processing，Cardiff，Wales，2009：429-432.

[15]Stojnic M，Parvaresh F，Hassibi B.On the reconstruction of block-sparse signals with an optimal number of measurements[J].IEEE Trans on Signal Process，2009，57（8）：3075-3085.

[16]Yin J，Chen T.Direction-of-arrival estimation using a sparse representation of array covariance vectors[J].IEEE Trans on Signal Processing，2011，59（9）：4489-4493.

[17]Xu X，Wei X，Ye Z.DOA estimation based on sparse signal recovery utilizing weighted-norm penalty[J].IEEE Signal Processing Letters，2012，19（3）：155-158.

[18]Liu Z M，Huang Z T，Zhou Y Y.Direction-of-arrival estimation of wideband signals via covariance matrix sparse representation[J].IEEE Trans on Signal Processing，2012，59（9）：4256-4270.

[19]He Z Q，Liu Q H，Jin L N，et al.Low complexity method for DOA estimation using array covariance matrix sparse representation[J].Electronics Letters，2013，49（3）：228-230.

[20]Ren Xiaoli，Wan Qun，Chen Hui.A fast method for DOA estimation of coherent signal from sparse signal reconstruction perspective[C]//Proc of the 7th IntConfon Wireless Communications，Networking and Mobile Computing，2011：2754-2757.