考慮電源不確定性的電力系統靈活性評價

錢彧呈

（上海電力新能源發展有限公司，上海200010）

1 研究背景與研究意義

在現代電力系統中，可再生能源發電的電源不確定性、電網結構不確定性以及電力系統負荷功率不確定性，此三者構成電力系統運行過程中功率分布不確定性的三大主要因素（圖1），需要電力系統對其具有一定的應變能力和響應能力，也就是所謂的靈活性，以此來盡可能地減小或消除以上不確定因素所帶來的負面影響，從而保證電力系統運行的安全和穩定。而接入了風電的電力系統，由于電源出力的不確定性，將會造成電源不確定性，從而導致有功功率波動，并因此對電力系統的穩定運行產生影響。

圖1 功率分布不確定性的三大主要因素

本文的研究對象就是對于應對電源不確定性的電力系統靈活性的評價方案。

2 電力系統靈活性評價概念

電力系統靈活性，是電力系統的四大固有屬性之一（其余三者為經濟性、可靠性和安全性）。因此，對電力系統靈活性的評價，是對電力系統穩定能力的一個直觀反映，研究電力系統對有功功率波動的承受能力，則是評價其靈活性的基礎。

其次，由于電網的有功功率波動，其波動性存在向上波動和向下波動的方向性，因此，電力系統靈活性也相應地具有方向性，即向上靈活性或向下靈活性。

3 風力發電機出力波動的最優潮流模型

3.1 優化模型的一般形式

本文中以電力系統對電源不確定性的最大承受能力的評價為基礎，對電力系統靈活性進行評價，其中以風電場作為不確定電源，通過由于風電場出力波動所導致的有功功率波動的角度來表現其不確定性。

在進行電力系統優化分析計算時，經常通過最優潮流（OPF）模型對系統中的一個或多個目標函數進行優化，該模型的一般數學表達式可以用如式（1）所示的數學模型表示：

式中，x 表示狀態變量；u表示控制變量向量；f（x，u）表示目標函數；g（x，u）表示等式約束；h（x，u）表示不等式約束。

本文中，f（x，u）是由于風電機處理波動導致的有功功率變化值的最大值（即maxΔPG）；等式約束g（x，u）包括對非風力發電機的等式約束和對風力發電機的等式約束；不等式約束h（x，u）包括對發電機出力、節點電壓和線路有功功率三者的不等式約束。

3.2 最優潮流模型的建立

3.2.1 目標函數

本文中，通過尋找電力系統所能承受的最大有功功率波動來評估電源不確定條件下的電力系統靈活性，因此，最優潮流模型的目標函數如式（2）所示：

3.2.2 等式約束

對于最優潮流問題中的等式約束g（x，u），一般為節點功率平衡約束，進一步可分為節點有功功率平衡方程與無功功率平衡方程，在本文中則要分為對于風機節點和對于非風機節點兩種情況的平衡方程：

對于非風機節點，等式約束如式（3）所示：

式中，PGi表示節點i發電機發出的有功功率；QGi表示節點i 發電機發出的無功功率；Pi（u，x）為節點i的節點注入有功功率；Qi（u，x）為節點i的節點注入無功功率；PLi和QLi則分別為節點i的有功負荷功率和無功負荷功率。

其中，節點注入功率Pi（u，x）和Qi（u，x）具體展開如式（4）和式（5）所示：

式中，j為節點i 的各個分支節點；Gij為i 與j 之間的電導；Bij為i與j 之間的電納；θij為i與j 之間的相角差（θij＝θi－θj）。

而對于風機節點，等式約束如式（6）所示：

式（6）等價于式（7）：

式中，α為風力發電機出力波動導致的有功功率下降百分比；ΔPG為下降的有功功率。

PGi、α、ΔPG之間存在關系如式（8）所示：

3.2.3 不等式約束

在最優潮流問題中，不等式約束h（x，u）是使電網運行安全可靠的重要保證。

不等式約束通常包含許多方面的內容，在本文中不等式約束主要包括：節點i上發電機的出力范圍，即有功功率和無功功率范圍，節點i的電壓幅值范圍以及通過有功功率潮流約束形式表示的輸電線路容量的限制。

具體如式（9）所示：

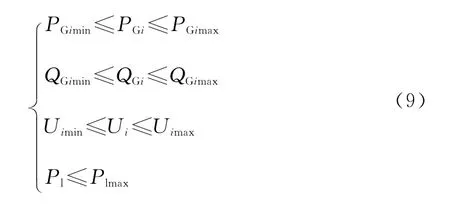
3.2.4 優化模型的建立

將式（2）、（3）、（6）、（9）代入式（1），即可得到完整的OPF模型，如式（10）所示：

其中，

在以上模型中，等式約束g（x，u）和不等式約束h（x，u）都具有確定的表達方式，式子右邊為約束邊界，并且該邊界是唯一確定的，在邊界內部則是可行解域。

可行解域具有剛性的表達方式，其邊界是不可逾越的，在邊界以外的解，即使其非常接近約束邊界，也依舊被認為是不可行解。

最優解所對應的系統，其運行狀態必須嚴格滿足等式約束和不等式約束。

換而言之，不滿足任一等式約束或不等式約束的解，都不是可行解，如果沒有一個解可以同時滿足所有的等式約束和不等式約束，則認為上述優化問題是無解的。

4 仿真與計算

4.1 MATPOWER 仿真算例分析

本文以MATPOWER4.1中的IEEE30節點為算例進行仿真，并運用runopf.m 程序進行潮流計算，再分別對節點參數和電機參數進行重新設置，在不同負荷和不同時間尺度共四種情況下，分析通過最優潮流計算得出的能保持系統穩定運行的最小有功功率，即所能承受的最大有功功率變化值（maxΔPG），以得出結論。

4.2 初始數據

在IEEE30節點中，共有6個節點是電機，其節點序號分別為1、2、13、22、23、27，其中節點1為平衡節點。

本文中將以節點2作為風機節點，通過改變其電機出力和有功功率上下限來對風機出力波動進行模擬。

表1和表2分別是IEEE30節點的初始電機出力數據和初始最優潮流數據。

表1 初始電機出力數據

表2 初始最優潮流數據

通過表1 可以看出，每個節點的電機都留有比較大的裕度，由于后文將對電機節點2的有功出力進行減小，從而對風機出力波動進行仿真，較大的裕度將會對結果造成很大影響，因此后文將會對除節點2之外的節點的最大有功出力進行適當調整。

而在表2中，PG和QG分別為電機節點的輸出有功和無功功率，PL和QL分別為母線注入負荷的有功和無功功率，BS為電納，在此用來反映無功補償，Type表示母線類型。其中節點1為平衡節點母線，節點2、13、22、23、27為PV 節點母線，其余節點均為PQ 節點母線。

4.3 系統可承受的最大有功功率波動

將2號節點的電機考慮成風力發電機，因此將其有功出力上下限（Pmax、Pmin）調至與其有功出力相同，并手動減小其有功出力，直至潮流不收斂；并將其余節點的有功功率上限適當調低以減小其出力裕度，其余五個節點的有功功率下限依舊是0。具體電機出力和最優潮流數據如表3、表4所示。

表3 電機出力數據（不考慮時間尺度的2號節點最小出力）

表4 最優潮流數據（不考慮時間尺度的2號節點最小出力）

通過調整計算，當節點2 的風機有功出力降至3.86 MW時，最優潮流結果不收斂。因此，3.87 MW 是系統運行穩定所需的最小有功出力，即此系統可以承受的最大有功功率下降波動為60.97－3.87＝57.1 MW。

同時由表4可知，由于節點2風機出力減小至3.87 MW，除了平衡節點1之外，其余四個節點的有功出力均比初始狀態要大，且都接近或已經達到其有功出力上限，但總的有功出力還是較初始狀態要小。由此可見，傳統電機的發電能力會對電力系統靈活性產生影響。

4.4 1.05倍有功負荷條件下系統可承受的最大有功功率波動

本節將對1.05 倍有功負荷條件下的系統進行仿真和計算，以此來分析不同負荷條件對系統承受有功功率波動能力的影響，即對系統靈活性的影響。具體電機出力和最優潮流數據如表5、表6所示。

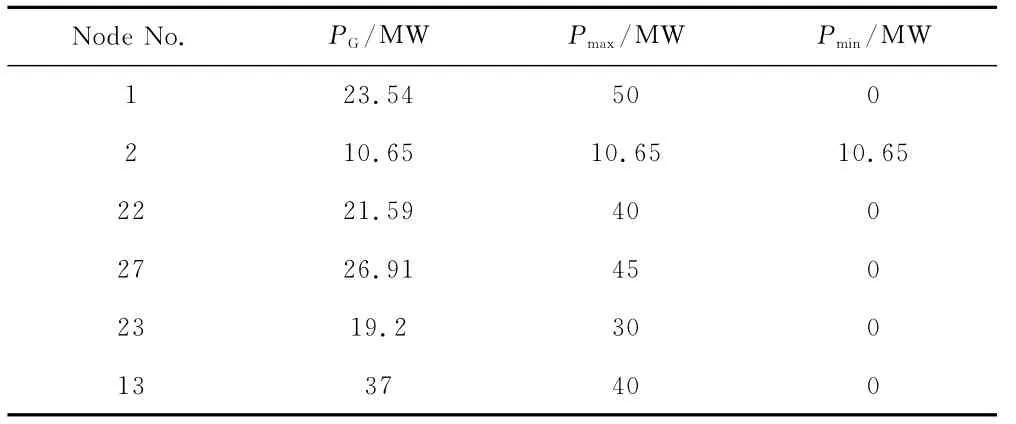
表5 電機出力數據（1.05倍有功負荷條件下節點2風機最小有功出力）

表6 最優潮流數據（1.05倍有功負荷條件下節點2風機最小有功出力）

通過調整計算，當節點2的風機有功出力降至10.64MW 時，最優潮流結果不收斂。因此，10.65MW 是在不考慮時間尺度的條件下，1.05倍負荷系統運行穩定所需的最小有功出力，即此系統可以承受的最大有功功率下降波動為60.97－10.65＝50.32MW。由此可知，當系統的有功負荷變大，且除風機外的其余發電機有功出力及出力上限不變的情況下，系統所能承受的最大有功功率波動會變小，即系統靈活性會相應地變差。

5 結論

本文通過建模仿真，主要研究了電力系統對由于風電出力波動導致的有功功率波動的承受能力，并主要得出了以下結論：

（1）當風力發電機的有功出力下降時，電力系統可以通過提高其余常規發電的有功出力來滿足系統的有功負荷要求，但這是建立在傳統發電留有足夠裕度的前提下。因此，電力系統中的傳統發電能力將會對電力系統靈活性產生影響。

（2）不同的負荷要求也會對電力系統的靈活性產生影響。在傳統電機有功出力上限不變的情況下，負荷越高，電力系統對于有功功率波動的承受能力越弱，電力系統的靈活性也相應地越差。

［1］孫偉卿.智能電網規劃與運行控制的柔性評價及分析方法［D］.上海：上海交通大學，2013.

［2］Lannoye E，Flynn D，O＇Malley M.Evaluation of Power System Flexibility［J］.IEEE Transactions on Power Systems，2012，27（2）：922－931.

［3］韓小琪，宋璇坤，李冰寒，等.風電出力變化對系統調頻的影響［J］.中國電力，2010，43（6）：26－29.

［4］戚永志，劉玉田.風電高風險爬坡有限度控制［J］.中國電機工程學報，2013，33（13）：69－75.