復(fù)合功率分流混合電動(dòng)轎車(chē)驅(qū)動(dòng)模式切換的協(xié)調(diào)控制*
趙治國(guó),代顯軍,王 晨,,張 彤,袁喜悅
(1.同濟(jì)大學(xué)新能源汽車(chē)工程中心,上海 201804; 2.上海華普汽車(chē)有限公司,上海 201501)
?
2015046
復(fù)合功率分流混合電動(dòng)轎車(chē)驅(qū)動(dòng)模式切換的協(xié)調(diào)控制*
趙治國(guó)1,代顯軍1,王 晨1,2,張 彤2,袁喜悅1
(1.同濟(jì)大學(xué)新能源汽車(chē)工程中心,上海 201804; 2.上海華普汽車(chē)有限公司,上海 201501)
為對(duì)帶雙行星排復(fù)合功率分流的混合動(dòng)力轎車(chē)驅(qū)動(dòng)模式切換過(guò)程中的轉(zhuǎn)矩進(jìn)行協(xié)調(diào)控制,采用基于轉(zhuǎn)矩解耦的控制方法來(lái)求解不同切換階段動(dòng)力源的目標(biāo)轉(zhuǎn)矩。在此基礎(chǔ)上,針對(duì)切換過(guò)程中輸出端轉(zhuǎn)矩波動(dòng)和發(fā)動(dòng)機(jī)實(shí)際轉(zhuǎn)矩難以精確確定等問(wèn)題,提出了基于發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì)和電機(jī)轉(zhuǎn)矩補(bǔ)償?shù)哪J角袚Q協(xié)調(diào)控制策略,并在Matlab/Simulink軟件平臺(tái)下進(jìn)行仿真驗(yàn)證。結(jié)果表明,該協(xié)調(diào)控制策略能有效降低切換過(guò)程中輸出端的轉(zhuǎn)矩波動(dòng)和整車(chē)的沖擊度。
發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì);功率分流;模式切換;協(xié)調(diào)控制
前言
混合動(dòng)力汽車(chē)在行駛過(guò)程中能根據(jù)工況要求自動(dòng)切換運(yùn)行模式,模式切換過(guò)程中整車(chē)對(duì)發(fā)動(dòng)機(jī)和電機(jī)的轉(zhuǎn)矩需求變化明顯,由于發(fā)動(dòng)機(jī)與電機(jī)的轉(zhuǎn)矩響應(yīng)速度不同和離合器或制動(dòng)器自身非線性特性的影響,若在模式切換過(guò)程中控制不當(dāng),會(huì)直接導(dǎo)致動(dòng)力系統(tǒng)輸出端轉(zhuǎn)矩大幅度波動(dòng),并產(chǎn)生沖擊,從而影響車(chē)輛的行駛平順性[1-4]。
針對(duì)上述問(wèn)題,文獻(xiàn)[5]中以典型單軸并聯(lián)混合動(dòng)力轎車(chē)為研究對(duì)象,利用最優(yōu)控制法求解發(fā)動(dòng)機(jī)和電機(jī)在模式切換過(guò)程中不同階段的目標(biāo)轉(zhuǎn)矩,但該方法忽略了發(fā)動(dòng)機(jī)和電機(jī)的瞬態(tài)轉(zhuǎn)矩響應(yīng)特性的差異。文獻(xiàn)[6]中針對(duì)傳統(tǒng)并聯(lián)混合動(dòng)力轎車(chē),提出“發(fā)動(dòng)機(jī)轉(zhuǎn)矩開(kāi)環(huán)+發(fā)動(dòng)機(jī)轉(zhuǎn)矩動(dòng)態(tài)協(xié)調(diào)估計(jì)+電機(jī)轉(zhuǎn)矩補(bǔ)償”的動(dòng)態(tài)協(xié)調(diào)控制算法,但實(shí)際切換過(guò)程中發(fā)動(dòng)機(jī)轉(zhuǎn)矩在線估計(jì)算法不能滿(mǎn)足控制對(duì)實(shí)時(shí)性的要求。文獻(xiàn)[7]中針對(duì)一種雙模功率分流混合動(dòng)力系統(tǒng),探討了其從輸入功率分流模式切換到復(fù)合功率分流模式過(guò)程中變速器輸出端轉(zhuǎn)矩波動(dòng)問(wèn)題,并采用電機(jī)予以補(bǔ)償,有效抑制了其轉(zhuǎn)矩波動(dòng)。文獻(xiàn)[8]中以四輪驅(qū)動(dòng)混合動(dòng)力轎車(chē)為研究對(duì)象,針對(duì)其由純電動(dòng)驅(qū)動(dòng)模式切換到混合驅(qū)動(dòng)模式過(guò)程中駕駛性能變差問(wèn)題,以混雜系統(tǒng)切換為理論依據(jù),設(shè)計(jì)了無(wú)擾動(dòng)模式切換控制策略,但是這些方法皆未考慮發(fā)動(dòng)機(jī)轉(zhuǎn)矩的瞬態(tài)響應(yīng)特性。
本文中以一種復(fù)合功率分流混合動(dòng)力轎車(chē)為研究對(duì)象,對(duì)其從純電動(dòng)驅(qū)動(dòng)模式切換到混合驅(qū)動(dòng)模式的動(dòng)態(tài)過(guò)程進(jìn)行動(dòng)力學(xué)分析,并基于特有的行星齒輪機(jī)構(gòu)的約束關(guān)系,利用實(shí)時(shí)可測(cè)的電機(jī)轉(zhuǎn)矩直接推算發(fā)動(dòng)機(jī)實(shí)際執(zhí)行轉(zhuǎn)矩,提出了基于發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì)和電機(jī)轉(zhuǎn)矩補(bǔ)償?shù)哪J角袚Q動(dòng)態(tài)協(xié)調(diào)控制策略,并在Matlab/Simulink平臺(tái)進(jìn)行仿真驗(yàn)證,結(jié)果表明,該協(xié)調(diào)控制策略能有效降低切換過(guò)程中輸出端的轉(zhuǎn)矩波動(dòng)和整車(chē)的沖擊度,提高了車(chē)輛的行駛平順性。
1 復(fù)合功率分流系統(tǒng)結(jié)構(gòu)
文中所研究的復(fù)合功率分流動(dòng)力系統(tǒng)結(jié)構(gòu)簡(jiǎn)圖[9]如圖1所示,主要由發(fā)動(dòng)機(jī)、大電機(jī)MG2(motor/generator)、小電機(jī)MG1、濕式制動(dòng)器B1(brake)、B2和功率分流裝置組成。其中功率分流裝置為共用行星架和齒圈的雙行星輪系結(jié)構(gòu),如圖2所示。圖中,S1為前排輪系小太陽(yáng)輪;P1為前排輪系短(粗)行星輪;P2為后排輪系長(zhǎng)(細(xì))行星輪;S2為后排輪系大太陽(yáng)輪;CR12為前后排輪系共用行星架;R12為前后排輪系共用齒圈。
發(fā)動(dòng)機(jī)連接行星架,小電機(jī)MG1連接前排小太陽(yáng)輪,大電機(jī)MG2連接后排大太陽(yáng)輪,三者動(dòng)力經(jīng)共用的齒圈復(fù)合后傳遞至輸出端。制動(dòng)器B1用于純電動(dòng)驅(qū)動(dòng)時(shí)鎖止發(fā)動(dòng)機(jī),提高系統(tǒng)效率,制動(dòng)器B2用于高速時(shí)鎖止小電機(jī)MG1,以避免其提供平衡轉(zhuǎn)矩,防止電功率循環(huán)[10]。該復(fù)合功率分流系統(tǒng)典型工作模式如表1所示。

表1 復(fù)合功率分流系統(tǒng)典型工作模式
2 切換過(guò)程建模和轉(zhuǎn)矩解耦控制
2.1 動(dòng)力系統(tǒng)動(dòng)態(tài)建模
復(fù)合功率分流混合動(dòng)力轎車(chē)具有多個(gè)工作模式,不同模式下動(dòng)力源的目標(biāo)轉(zhuǎn)矩有所不同。為方便分析,求解切換過(guò)程中的動(dòng)力源目標(biāo)轉(zhuǎn)矩,對(duì)動(dòng)力系統(tǒng)結(jié)構(gòu)進(jìn)行簡(jiǎn)化,將車(chē)輪轉(zhuǎn)動(dòng)慣量和車(chē)輛平動(dòng)質(zhì)量統(tǒng)一折算到變速器輸出軸,忽略旋轉(zhuǎn)黏性阻尼、軸承與軸承座間的彈性和齒輪嚙合彈性,得到如圖3所示的動(dòng)力學(xué)模型。圖中TICE在發(fā)動(dòng)機(jī)點(diǎn)火之前為拖轉(zhuǎn)阻力矩,點(diǎn)火后為驅(qū)動(dòng)轉(zhuǎn)矩,αICE為發(fā)動(dòng)機(jī)角加速度,JICE為發(fā)動(dòng)機(jī)等效轉(zhuǎn)動(dòng)慣量(包括曲軸、飛輪、制動(dòng)器B1從動(dòng)盤(pán)和行星架CR12),TCR12為行星架端轉(zhuǎn)矩,TMG1為電機(jī)MG1轉(zhuǎn)矩,αMG1為其角加速度,JMG1為電機(jī)MG1端等效轉(zhuǎn)動(dòng)慣量(包括電機(jī)MG1轉(zhuǎn)子、太陽(yáng)輪S1),TS1為太陽(yáng)輪S1端轉(zhuǎn)矩,TMG2為電機(jī)MG2轉(zhuǎn)矩,αMG2為其角加速度,JMG2為電機(jī)MG2端等效轉(zhuǎn)動(dòng)慣量(包括電機(jī)MG2轉(zhuǎn)子、太陽(yáng)輪S2),TS2為太陽(yáng)輪S2端轉(zhuǎn)矩,TR12為齒圈端轉(zhuǎn)矩,JR12為折算到齒圈端的等效轉(zhuǎn)動(dòng)慣量(包括齒圈R12、半軸、車(chē)輪、整車(chē)),αR12為齒圈輸出端角加速度,TL為折算到齒圈輸出端的等效阻力矩。
行星排各軸上的轉(zhuǎn)矩方程為
TICE-JICEαICE=TCR12
(1)
TMG1-JMG1αMG1=TS1
(2)
TMG2-JMG2αMG2=TS2
(3)
行星排轉(zhuǎn)矩平衡方程為
TCR12+TR12+TS1+TS2=0
(4)
TR12+i1TS1+i2TS2=0
(5)
角加速度關(guān)系方程為
αMG1=i1αR12+(1-i1)αICE
(6)
αMG2=i2αR12+(1-i2)αICE
(7)
式中:i1、i2分別為前后行星排傳動(dòng)比。由式(1)~式(7)所組成的線性方程組共有16個(gè)變量,其中已知變量5個(gè),分別為JICE、JMG1、JMG2、i1和i2;未知變量11個(gè),分別為T(mén)ICE、TMG1、TMG2、TCR12、TS1、TS2、TR12、αICE、αMG1、αMG2和αR12。只須再根據(jù)整車(chē)不同模式任意給定其中4個(gè)參數(shù),即可求解其他變量。根據(jù)系統(tǒng)動(dòng)態(tài)轉(zhuǎn)矩控制的需求,通過(guò)求取有用的函數(shù)組合,可以求解出目標(biāo)轉(zhuǎn)矩TICE、TMG1、TMG2,分別作為發(fā)動(dòng)機(jī)、電機(jī)MG1和電機(jī)MG2各自控制器的轉(zhuǎn)矩控制指令。
假定已知TMG1、TR12、αICE、αR12,此種情況下求取目標(biāo)轉(zhuǎn)矩TMG2、TICE,將要求解的轉(zhuǎn)矩計(jì)算函數(shù)命名為T(mén)MG2_TICE_fun(TMG1,TR12,αICE,αR12),聯(lián)立式(1)~式(7),利用Matlab求解方程組即可求解,鑒于篇幅原因,這里不再贅述。
2.2 純電動(dòng)驅(qū)動(dòng)模式切換到混合驅(qū)動(dòng)模式過(guò)程分析和轉(zhuǎn)矩解耦控制
整車(chē)模式切換協(xié)調(diào)控制流程如圖4所示。車(chē)輛起步首先以純電動(dòng)模式行駛,當(dāng)駕駛員轉(zhuǎn)矩需求Treq大于純電動(dòng)最大轉(zhuǎn)矩閾值TEV_max、蓄電池SOC小于最低閾值SOC_low或要求車(chē)速v大于純電動(dòng)最大車(chē)速閾值vEV_max時(shí),整車(chē)控制器接收模式切換請(qǐng)求信號(hào),制動(dòng)器B1迅速打開(kāi),并進(jìn)行MG1、MG2轉(zhuǎn)矩協(xié)調(diào)控制,等到B1完全打開(kāi)后,MG1、MG2協(xié)調(diào)控制輸出轉(zhuǎn)矩拖轉(zhuǎn)發(fā)動(dòng)機(jī),當(dāng)其轉(zhuǎn)速nICE大于怠速轉(zhuǎn)速nidle后,發(fā)動(dòng)機(jī)點(diǎn)火,進(jìn)入混合驅(qū)動(dòng)模式。由于發(fā)動(dòng)機(jī)瞬態(tài)轉(zhuǎn)矩響應(yīng)的延時(shí),須適時(shí)估計(jì)其動(dòng)態(tài)轉(zhuǎn)矩并利用MG1、MG2進(jìn)行轉(zhuǎn)矩補(bǔ)償協(xié)調(diào)控制,以滿(mǎn)足駕駛員的轉(zhuǎn)矩需求,降低輸出端的轉(zhuǎn)矩波動(dòng),減小車(chē)輛沖擊。整個(gè)模式切換過(guò)程包括B1鎖止時(shí)的純電動(dòng)、B1打開(kāi)過(guò)程的純電動(dòng)、起動(dòng)和混合動(dòng)力4個(gè)階段。
2.2.1 B1鎖止時(shí)的純電動(dòng)階段
利用杠桿法[11-12]分析此階段系統(tǒng)的工作狀況,如圖5所示。大電機(jī)MG2提供驅(qū)動(dòng)轉(zhuǎn)矩TMG2,制動(dòng)器B1鎖止,提供平衡轉(zhuǎn)矩TB1,兩者合力矩與輸出端OUT阻力矩TL平衡,小電機(jī)MG1空轉(zhuǎn)。此階段轉(zhuǎn)矩控制框圖如圖6所示。
此階段的已知變量、目標(biāo)變量和轉(zhuǎn)矩求解函數(shù)如表2中序號(hào)(a)所示,其中TR12利用車(chē)速和踏板行程從駕駛員轉(zhuǎn)矩需求MAP查得,再根據(jù)TR12求得該階段大電機(jī)MG2、制動(dòng)器B1的目標(biāo)轉(zhuǎn)矩分別為

表2 不同階段目標(biāo)轉(zhuǎn)矩求解
TMG2=-TR12/i2
(8)
(9)
2.2.2 B1打開(kāi)過(guò)程的純電動(dòng)階段
當(dāng)車(chē)輛加速或需要爬坡時(shí),純電動(dòng)滿(mǎn)足不了需求,須起動(dòng)發(fā)動(dòng)機(jī),此時(shí)制動(dòng)器B1迅速打開(kāi),為控制發(fā)動(dòng)機(jī)在零轉(zhuǎn)速點(diǎn),大小電機(jī)轉(zhuǎn)矩TMG1、TMG2共同驅(qū)動(dòng),此階段系統(tǒng)等效杠桿和控制框圖分別如圖7和圖8所示。
此階段的已知變量、目標(biāo)變量和轉(zhuǎn)矩求解函數(shù)如表2中序號(hào)(b)所示,其中TICE等于制動(dòng)器B1傳遞的轉(zhuǎn)矩TB1,求得該階段電機(jī)MG1、MG2的目標(biāo)轉(zhuǎn)矩分別為
(10)
(11)
2.2.3 起動(dòng)發(fā)動(dòng)機(jī)階段
等到制動(dòng)器B1完全打開(kāi)后,小電機(jī)MG1在當(dāng)前純電動(dòng)驅(qū)動(dòng)轉(zhuǎn)矩TMG1上疊加額外拖轉(zhuǎn)轉(zhuǎn)矩TMG1′拖轉(zhuǎn)發(fā)動(dòng)機(jī)至怠速轉(zhuǎn)速。同時(shí),大電機(jī)MG2在當(dāng)前純電動(dòng)驅(qū)動(dòng)轉(zhuǎn)矩TMG2上疊加補(bǔ)償轉(zhuǎn)矩TMG2′以消除MG1拖轉(zhuǎn)轉(zhuǎn)矩對(duì)輸出端造成的影響,此階段系統(tǒng)等效杠桿和控制框圖分別如圖9和圖10所示。
此階段的已知變量、目標(biāo)變量和轉(zhuǎn)矩求解函數(shù)如表2中序號(hào)(c)所示,TICE為發(fā)動(dòng)機(jī)的拖轉(zhuǎn)阻力矩,通過(guò)電機(jī)控制器反饋比較準(zhǔn)確的電機(jī)轉(zhuǎn)速nMG1、nMG2計(jì)算得到發(fā)動(dòng)機(jī)的實(shí)際轉(zhuǎn)速nICE,從發(fā)動(dòng)機(jī)拖轉(zhuǎn)阻力矩MAP查得其阻力轉(zhuǎn)矩TICE,發(fā)動(dòng)機(jī)的角加速度可根據(jù)目標(biāo)怠速轉(zhuǎn)速nidle和起動(dòng)時(shí)間確定。該階段電機(jī)MG1、MG2的目標(biāo)轉(zhuǎn)矩分別為
TMG1=((i2-1)TR12+i2TICE-(JMG1(i1-1)(i1-i2)+
i2JICEαICE))/(i1-i2)
(12)
TMG2=-((JMG2(i2-1)(i1-i2)-i1JICE)αICE+
(i1-1)TR12+i1TICE)/(i1-i2)
(13)
2.2.4 混合動(dòng)力階段
當(dāng)發(fā)動(dòng)機(jī)轉(zhuǎn)速達(dá)到怠速轉(zhuǎn)速后,迅速?lài)娪忘c(diǎn)火,發(fā)動(dòng)機(jī)、MG1、MG2共同輸出轉(zhuǎn)矩,驅(qū)動(dòng)車(chē)輛行駛。由于發(fā)動(dòng)機(jī)動(dòng)態(tài)轉(zhuǎn)矩響應(yīng)的延遲,須估算出其實(shí)際發(fā)出的轉(zhuǎn)矩,利用MG1、MG2轉(zhuǎn)矩補(bǔ)償控制來(lái)滿(mǎn)足駕駛員的轉(zhuǎn)矩需求,此階段系統(tǒng)等效杠桿和控制框圖分別如圖11和圖12所示。
圖12中TICE_op、nICE_op分別為混合動(dòng)力階段發(fā)動(dòng)機(jī)的最優(yōu)目標(biāo)轉(zhuǎn)矩與最優(yōu)目標(biāo)轉(zhuǎn)速,可以根據(jù)動(dòng)力系統(tǒng)效率最優(yōu),利用當(dāng)前車(chē)速和踏板行程從發(fā)動(dòng)機(jī)最優(yōu)轉(zhuǎn)矩MAP和最優(yōu)轉(zhuǎn)速M(fèi)AP查得,得到的最優(yōu)發(fā)動(dòng)機(jī)目標(biāo)轉(zhuǎn)矩送入發(fā)動(dòng)機(jī)控制器,發(fā)動(dòng)機(jī)目標(biāo)角加速度利用當(dāng)前發(fā)動(dòng)機(jī)實(shí)際轉(zhuǎn)速和目標(biāo)發(fā)動(dòng)機(jī)轉(zhuǎn)速確定。
此階段的已知變量、目標(biāo)變量和轉(zhuǎn)矩求解函數(shù)如表2中序號(hào)(d)所示,函數(shù)中TICE為發(fā)動(dòng)機(jī)實(shí)際發(fā)出的轉(zhuǎn)矩,可根據(jù)式(1)~式(7)進(jìn)行估算:
TICE_estimate=((i1-1)(TMG1_act-JMG1αMG1)+(i2-1)·
(TMG2_act-JMG2αMG2)+JICE(αMG2i1+αMG1i2))/(i1+i2)
(14)
式中TMG1_act、TMG2_act可由電機(jī)控制器反饋的實(shí)際轉(zhuǎn)矩信號(hào)得到,αMG1、αMG2可由電機(jī)控制器反饋的實(shí)際轉(zhuǎn)速信號(hào)求導(dǎo)得到。求得該階段電機(jī)MG1、MG2的目標(biāo)轉(zhuǎn)矩分別為
TMG1=((i2-1)TR12+i2TICE_estimate-
(JMG1(i1-1)(i1-i2)+i2JICEαICE))/(i1-i2)
(15)
TMG2=-((JMG2(i2-1)(i1-i2)-i1JICE)αICE+
(i1-1)TR12+i1TICE_estimate)/(i1-i2)
(16)
3 仿真分析
利用Matlab/Simulink仿真平臺(tái)對(duì)所提出的轉(zhuǎn)矩協(xié)調(diào)控制策略進(jìn)行仿真驗(yàn)證,各關(guān)鍵零部件參數(shù)如表3所示,仿真結(jié)果如圖13和圖14所示。
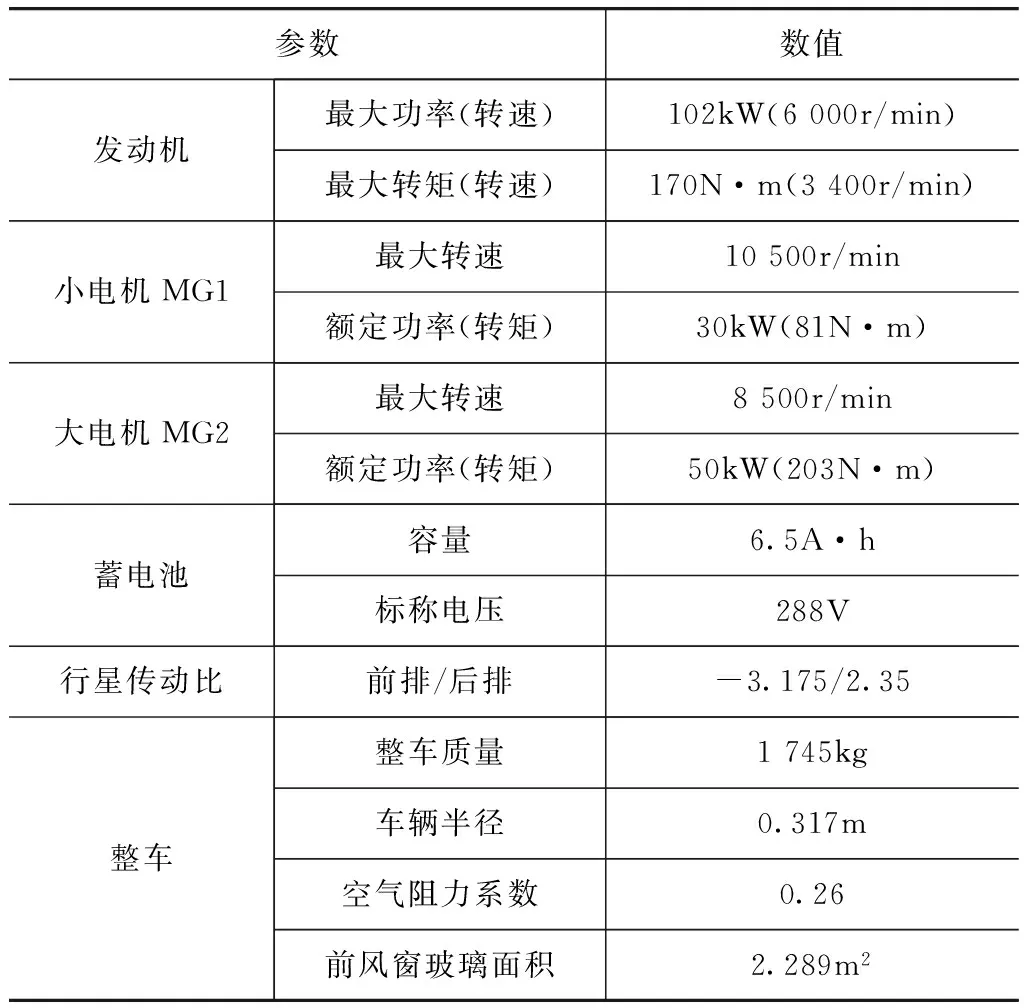
表3 動(dòng)力系統(tǒng)關(guān)鍵零部件參數(shù)
圖13為有無(wú)發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì)電機(jī)轉(zhuǎn)矩補(bǔ)償協(xié)調(diào)控制的對(duì)比仿真結(jié)果。圖中運(yùn)行模式不同的值代表不同階段,4、5、2、1分別表示B1鎖止純電動(dòng)階段、B1打開(kāi)純電動(dòng)階段、起動(dòng)階段和混合動(dòng)力階段。圖14為模式切換過(guò)程動(dòng)力源轉(zhuǎn)矩仿真結(jié)果。從圖13可以看出,整車(chē)控制器在8.15s發(fā)出模式切換指令,制動(dòng)器B1迅速打開(kāi),進(jìn)入純電動(dòng)階段,在8.35s B1完全打開(kāi)后,MG1、MG2協(xié)調(diào)控制拖轉(zhuǎn)發(fā)動(dòng)機(jī),發(fā)動(dòng)機(jī)從靜止到怠速的時(shí)間為0.3s,穩(wěn)定0.5s后,發(fā)動(dòng)機(jī)噴油點(diǎn)火進(jìn)入混合驅(qū)動(dòng)模式。此時(shí)如果不進(jìn)行發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì),僅進(jìn)行穩(wěn)態(tài)轉(zhuǎn)矩分配,即電機(jī)MG1、MG2未進(jìn)行轉(zhuǎn)矩補(bǔ)償控制,其轉(zhuǎn)矩會(huì)產(chǎn)生突變(見(jiàn)圖14中的實(shí)線),并且由于實(shí)際過(guò)程中發(fā)動(dòng)機(jī)瞬態(tài)轉(zhuǎn)矩的延遲,會(huì)導(dǎo)致齒圈輸出端的轉(zhuǎn)矩大幅波動(dòng),其峰峰值達(dá)68N·m,整車(chē)沖擊度較大,其絕對(duì)值的最大值大于德國(guó)的沖擊度限制值10m/s3;若進(jìn)行發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì),并利用估計(jì)值進(jìn)行電機(jī)轉(zhuǎn)矩補(bǔ)償協(xié)調(diào)控制,則電機(jī)MG1、MG2轉(zhuǎn)矩變化平緩(見(jiàn)圖14中的虛線),齒圈輸出端轉(zhuǎn)矩(發(fā)動(dòng)機(jī)和電機(jī)MG1與MG2轉(zhuǎn)矩的耦合結(jié)果)波動(dòng)峰峰值減小至32.5N·m,整車(chē)沖擊度小于其現(xiàn)值10m/s3。
仿真結(jié)果表明,基于發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì)+電機(jī)轉(zhuǎn)矩補(bǔ)償?shù)哪J角袚Q動(dòng)態(tài)協(xié)調(diào)控制策略能有效降低輸出端轉(zhuǎn)矩波動(dòng),減小切換過(guò)程車(chē)輛沖擊度,在滿(mǎn)足駕駛員轉(zhuǎn)矩需求的前提下,提高了車(chē)輛的行駛平順性。
4 結(jié)論
(1) 建立了復(fù)合功率分流混合動(dòng)力系統(tǒng)的動(dòng)力學(xué)模型,并基于轉(zhuǎn)矩解耦的控制方法來(lái)求解不同模式下動(dòng)力源的目標(biāo)轉(zhuǎn)矩,解決了功率分流系統(tǒng)多自由度的轉(zhuǎn)矩協(xié)調(diào)和轉(zhuǎn)矩平衡控制問(wèn)題。
(2) 利用杠桿法分析了系統(tǒng)從純電動(dòng)驅(qū)動(dòng)模式切換到混合驅(qū)動(dòng)模式每一階段的控制策略,并利用轉(zhuǎn)矩求解函數(shù)得到各階段動(dòng)力源的目標(biāo)轉(zhuǎn)矩,在此基礎(chǔ)上提出了發(fā)動(dòng)機(jī)轉(zhuǎn)矩估計(jì)+電機(jī)轉(zhuǎn)矩補(bǔ)償?shù)霓D(zhuǎn)矩協(xié)調(diào)控制策略,以抑制模式切換過(guò)程中輸出端的轉(zhuǎn)矩波動(dòng)。
(3) 所提出的模式切換轉(zhuǎn)矩協(xié)調(diào)控制策略能夠有效減小復(fù)合功率分流混合動(dòng)力系統(tǒng)由純電動(dòng)驅(qū)動(dòng)模式切換到混合驅(qū)動(dòng)模式過(guò)程中輸出端轉(zhuǎn)矩波動(dòng)和整車(chē)的沖擊度,提高了車(chē)輛的行駛平順性。
[1] Kim Sangjoon, Park Joonyoung. Transient Control Strategy of Hybrid Electric Vehicle During Mode Change [C]. SAE Paper 2009-01-0228.
[2] 侯獻(xiàn)軍,杜常清,顏伏伍,等.混合動(dòng)力系統(tǒng)狀態(tài)切換技術(shù)研究[J].內(nèi)燃機(jī)工程,2009,30(6):72-76.
[3] 古艷春,殷承良,張建武.并聯(lián)混合動(dòng)力汽車(chē)轉(zhuǎn)矩協(xié)調(diào)控制策略仿真研究[J].系統(tǒng)仿真學(xué)報(bào),2007,19(3):170-175.
[4] 王慶年,趙子亮,劉東秦.并聯(lián)混合動(dòng)力汽車(chē)控制策略與仿真分析研究[J].機(jī)械工程學(xué)報(bào),2005,41(12):13-18.
[5] Koprubasi K, Westervelt E R, Rizzoni G. Toward the Systematic Design of Controllers for Smooth Hybrid ElectricVehicle Mode Changes[C]. The American Automatic Control Council, Proceedings of the 2007 American Control Conference, New York, AACC,2007:2985-2990.
[6] 童毅,歐陽(yáng)明高,張俊智.并聯(lián)式混合動(dòng)力汽車(chē)控制算法的實(shí)時(shí)仿真研究[J].機(jī)械工程學(xué)報(bào),2003,39(10):158-160.
[7] Choi W, Kang J, Hong S, et al. Development of a Control Algorithm to Reduce Torque Variation for the Dual Mode HEV During Mode Change[C]. Vehicle Power and Propulsion Conference (VPPC),2011:1-6.
[8] 趙治國(guó),何寧,朱陽(yáng),等.四輪驅(qū)動(dòng)混合動(dòng)力轎車(chē)驅(qū)動(dòng)模式切換控制[J].機(jī)械工程學(xué)報(bào),2011,47(4):100-109.
[9] Yu Haisheng, Zhang Jianwu, Zhang Tong. Control Strategy Design and Experimental Research on a Four-Shaft Electronic Continuously Variable Transmission Hybrid Electric Vehicle[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2012,226(12):1594-1612.
[10] Schulz M. Circulating Mechanical Power in a Power-Split Hybrid Electric Vehicle Transmission[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering,2004,218(12):1419-1425.
[11] 馮櫻.運(yùn)用杠桿法計(jì)算汽車(chē)行星齒輪變速器的傳動(dòng)[J].湖北汽車(chē)工業(yè)學(xué)院學(xué)報(bào),2008,22(3):17-20.
[12] Bendord H, Leising M. The Lever Analogy: a New Tool in Transmission Analysis[C]. SAE Paper 810102.
Coordinated Control of Driving Mode Switching ofCompound Power-Split Hybrid Electric Car
Zhao Zhiguo1, Dai Xianjun1, Wang Chen1,2, Zhang Tong2& Yuan Xiyue1
1.CleanEnergyAutomotiveEngineeringCenter,TongjiUniversity,Shanghai201804; 2.ShanghaiMapleAutomobileCo.,Ltd.,Shanghai201501
For the coordinated control of torque in the driving-mode switching process of a hybrid electric car with double-planetary-gear-based compound power split system, a control technique based on torque decoupling is adopted to solve out the objective torque of power source at different switching phases. On this basis, aiming at the problem of output torque ripple and the difficulty in accurately determining the actual torque of engine, a coordinated control strategy for driving-mode switching is proposed based on engine torque estimation and motor torque compensation, and a verification simulation is conducted on Matlab/Simulink platform. The results show that the proposed strategy can effectively reduce the output torque ripple and vehicle jerk in driving-mode switching process.
engine torque estimation; power split; mode switching; coordinated control
*國(guó)家自然科學(xué)基金(51275355)和國(guó)家863計(jì)劃項(xiàng)目(2012AA111201)資助。
原稿收到日期為2014年8月13日,修改稿收到日期為2014年11月15日。

