基于空間自回歸和空間聚類的漁情預報模型

袁紅春, 譚明星, 顧怡婷, 陳新軍

(上海海洋大學: 1.信息學院; 2.海洋科學學院, 上海 201306)

傳統的遠洋漁情預報中, 多數學者采用多元線性回歸方法定量地對環境數據及漁獲數據進行分析,獲得預報模型。如沈金鰲等[1]通過多元線性回歸分析,將帶魚的資源量指數、各汛期的總捕撈努力量及長江徑流量作為預報因子建立模型, 預報嵊山冬季帶魚(Trichiurus lepturus)魚汛期的漁獲量。陳新軍等[2]在分析東黃海鮐(Scomber japonicus)的漁場時, 采用廣義線性模型(Generalized Linear Model, GLM)和廣義可加模型(Generalized Additive Model, GAM), 結合海洋環境因子建立預報模型, 以分析漁場資源的形成機制。陳新軍等[3-4]研究了西北太平洋柔魚(Ommastrephes batrami)漁場與環境因子的內在關系,利用月相對光誘魷釣作業的影響, 證明月相對日產量的影響顯著。但由于環境數據和漁獲數據之間的關系并非線性的, 傳統的線性回歸預報模型不能準確地預測漁情信息。隨著人工智能的崛起, 近年來有學者將人工智能技術用于漁情預測。杜云艷等[5]采用空間聚類方法建立關于漁業數據和對應水溫間的時空分布模型。袁紅春等[6]利用BP(Back Propagation)神經網絡預報西北太平洋柔魚漁獲情況。張月霞等[7]利用案例推理預報東海區鮐魚中心漁場。但單純的空間聚類、專家系統、人工神經網絡或案例推理方法并不能準確地反應漁業數據的時空分布。單獨的空間聚類只考慮空間因素, 忽略了其他因子的影響,從而導致預測誤差較大; 專家系統過于依靠專家知識經驗; 人工神經網絡的黑箱操作導致訓練結果不易理解。上述原因阻礙了人工智能在漁情預報中的應用。其他學者, 如 Masahiko等[8]、Mohri等[9]、Daniel等[10]分別研究了最適宜大眼金槍魚棲息的水溫范圍對產量的影響。日本的 Hiroaki[11]通過 GLM方法標準化印度洋大眼金槍魚的延繩釣漁獲量, 研究海洋環境與金槍魚漁獲量之間的關系。綜上, 現有方法僅用單一的模型描述整片海域中的漁情信息, 而同一片海域中不同位置的自然環境不同, 單一的模型不能準確地預報整體漁情。同時, 依據現有統計數據可知, 大量漁獲數據缺失, 因數據缺失而導致無法準確描述及研究環境和漁獲量之間的關系, 也是漁情預報過程中亟待解決的問題之一[12]。本研究以印度洋大眼金槍魚為例[13,14], 提出一種基于空間自回歸和空間聚類的動態漁情預測模型, 以豐富預測方法,提高預測水平。

1 材料與方法

1.1 數據來源

海洋環境數據(海面高度, 海表溫度, 葉綠素濃度)來源于美國國家海洋和大氣管理局, 漁業作業數據(漁獲量)來源于印度洋金槍魚委員會。

1.2 基于空間自回歸的數據預處理

1.2.1 數據的補缺

由于漁獲數據缺失嚴重, 若要利用該數據建立預測模型, 需進一步補全缺失數據[15]。本研究在傳統用于補全數據模型的基礎上增加修正項, 構建空間自回歸模型。首先, 給定觀察數據為一個n維向量Y, 表示漁業產量數據, 一個n×m的矩陣X為海洋環境數據(m為環境因子數)。假設Y中每一個因變量yi都互相影響, 即:yi=f(yj),i≠j。回歸方程可以修正成如下形式:

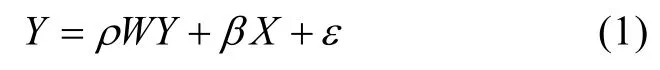
W是鄰接矩陣, 在回歸模型的空間拓展上起決定性作用。ρ是解釋變量和因變量之間空間獨立性強度的參數。殘差向量ε被假定為服從獨立同分布的標準正態分布,β是系數矩陣。

本研究用八-鄰居準則構建鄰接矩陣W。一個八-鄰居準則構建的矩陣見圖1。

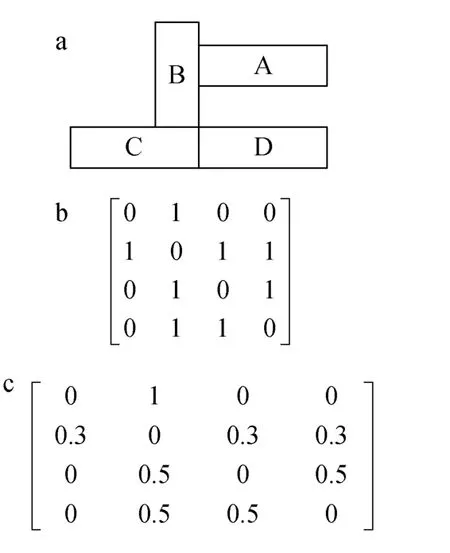
圖1 八-鄰居鄰接矩陣Fig.1 An eight-neighborhood its adjacency matrix

圖1(a)表示空間上A、B、C、D 4個單元格的位置關系, 圖1(b)表示每個點與其余點位置的關系矩陣。以矩陣第二行為例, 第二行表示單元格 B與其余單元格的位置關系, 因B與A有相鄰的邊、與C共享一條邊和一個頂點、與 D有相接的頂點, 所以第一列(A)為1, 第三列(C)為1, 第四列(D)為1, 其余位置為0。標記每個單元格與其他單元格之間的關系后, 得到圖1(b)中以二進制形式表示的鄰接矩陣。然后對鄰接矩陣中有標記的數值進行歸一化。具體方法為: 令每一行之和為 1, 即歸一化后的標記值為 1除以該行不為0的數值的個數。以第二行為例, 有標記的個數為3, 1/3約為0.3, 則每個有標記的值歸一化后均為0.3。

當ρ=0, 式(1)就變成傳統回歸方程。修正后的模型有以下優點: (1)殘差有很少的空間自相關性;(2)如果空間自相關系數在統計學上非常大, 就可以確定空間自相關存在的數量。這意味著因變量y變化的范圍是y到相鄰觀測值的平均值; (3)模型的擬合度很高。

選取產量數據不為零的數據作為數據集, 構建空間自回歸模型。模型建立后, 對空間缺失值進行插補, 插補方式為

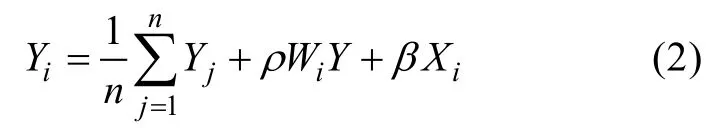
其中Yi為待預測的缺失產量數據,表示該預測區域內產量的平均值,Wi為空間標準加權矩陣W的第i行,Y是表示漁業產量的向量,Y中缺失產量用0表示。

1.2.2 數據的歸一化

為了研究印度洋大眼金槍魚延繩釣漁業產量與相應棲息地海域海洋環境因子的關系, 需要建立一種客觀標準反映該區域的資源豐度。單位捕撈努力量漁獲量(Catch Per Unit Effort, CPUE)的大小常被作為資源豐度的相對指數來反映資源豐度的變化, 其定義為

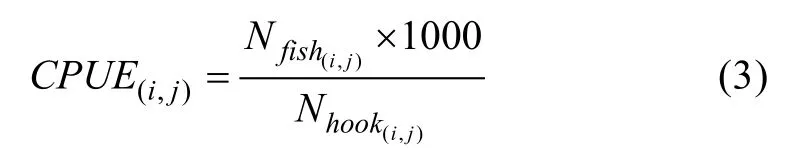
其中,CPUE(i,j)代表以經緯度(i,j)為起點的范圍5°×5°區域內釣獲率,Nfish(i,j)為該范圍內的漁獲尾數,Nhook(i,j)為該范圍內的下鉤枚數。CPUE(i,j)也可解釋為每千鉤上鉤的大眼金槍魚數量。再對單位捕撈努力量漁獲量進行處理, 使用相對資源指數(Relative Abundance Index, RAI)構建棲息地適宜性指數模型。相對資源指數由某一時間地點的單位捕撈努力量漁獲量值除以所有單位捕撈努力量漁獲量值中的最大值得到, 計算方法為

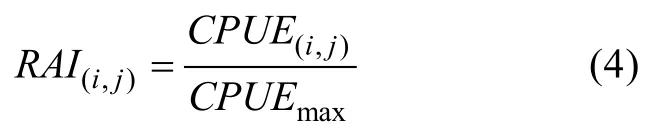
相對資源指數可看作反映棲息地質量的指標,等價于實際的棲息地適宜指數。

1.3 基于空間聚類的漁區劃分

根據環境數據及漁獲數據的相關性, 利用每條數據的地理位置信息進行 K-Means聚類, 把地理位置相對較近、漁獲數據之間相關系數較高的區域劃分為一類, 從而大大降低預測誤差。空間中數據對象的記錄主要包括空間實體的位置、形狀以及對象之間的相互關系, 這種關系通常以坐標或者拓撲的形式表示。本研究將每5°×5°區域看作空間上的一個實體點, 每個實體點包含地理位置數據(緯度, 經度)和產量數據(棲息地適宜性指數 HSI)。其中, 地理位置數據中的緯度和經度為實體點的空間數據, 產量數據 HSI為實體點的屬性數據。結合空間實體點的空間數據和屬性數據等多方面因素考慮, 并參考大量有關聚類分析的文獻后[16-18], 設計如下適用于漁情預報的空間聚類算法：

算法1 空間聚類算法

輸入: 地理位置數據和產量數據

輸出: 聚類結果

步驟如下:

(1) 確定待聚類數據集D, 聚類數K, 預設迭代次數m和收斂條件;

(2) 初始化聚類重心Ci;

(3) 計算每個數據Di到各個Ci的距離, 選取最近的距離歸并到該類中;

(4) 更新重心Ci;

(5) 計算所有Ci值的變化;

(6) 直到滿足收斂條件或達到迭代次數m, 停止迭代。

其中聚類重心的計算方法如下:

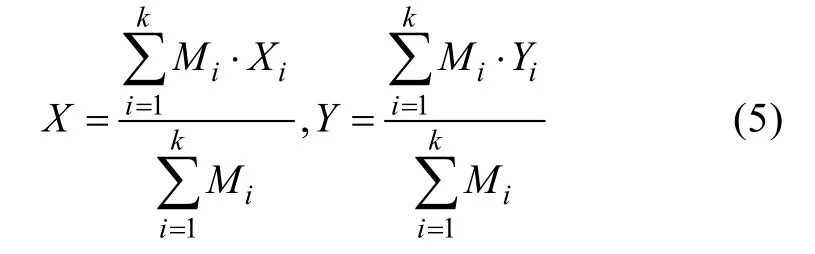
X為聚類重心的經度,Y為聚類重心的緯度,Mi為漁區i每個月的產量,Xi為漁區i重心點的經度,Yi為漁區i重心點的緯度, 漁區的個數為k。通過該聚類方法可以把地理位置相對較近、漁獲數據之間相關系數較高的區域劃分為一類, 從而減少因不同地理位置或不同環境所引起的誤差。

1.4 基于非線性回歸的棲息地適宜性指數模型

HSI模型在20世紀80年代由美國魚類和野生動物保護委員會提出[19-21], 被用來定量地描述野生動物的棲息地質量。

考慮到漁獲量的高低不僅與地理位置有關, 還與魚類生存的環境因子, 如海表溫度(SST)、海面高度(SSH)和葉綠素濃度(CHL-a)等有關。因此, 本研究針對每個環境因子, 利用其和棲息地適宜性指數之間的關系, 分別計算其對大眼金槍魚產量影響的適宜性指數(Suitability Index, SI); 最后, 通過回歸分析關聯各種SI值得到綜合HSI模型(圖2)。

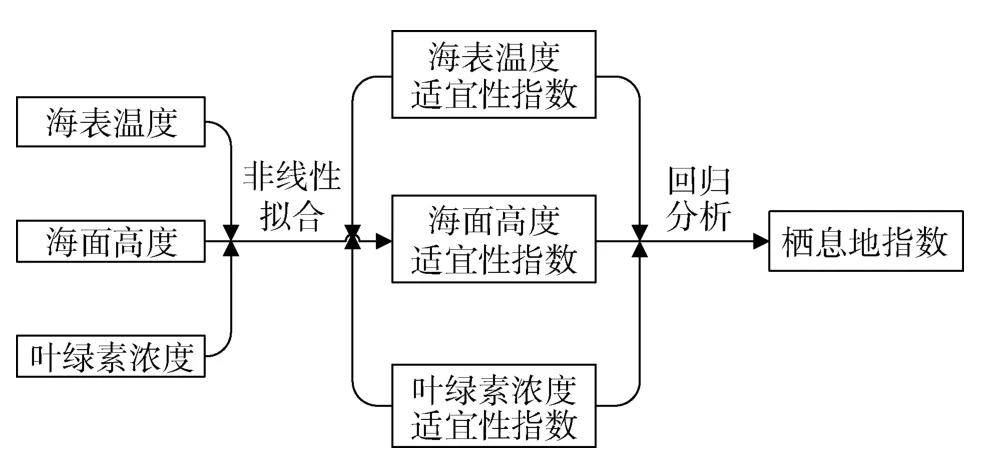
圖2 棲息地適宜性指數模型構建方法Fig.2 Method for constructing the habitat suitability index model

利用綜合優化分析計算軟件平臺——First Optimization的公式擬合工具箱, 對每個環境因子和其對應的 RAI分別作非線性擬合, 把最佳擬合公式作為棲息地適宜性指數計算公式中的單項棲息地適宜性指數SI, 通過對 3種環境因子在不同月份的擬合結果比較可知, 3種環境因子與棲息地適宜性指數的擬合形式可用如下形式表示:

其 中,A= （a1,a2, … ,a10）,B=（0 , 1,… ,9）,X=（x1,x2,… ,xm）′為環境因子。因此, 在計算參數A時,可先計算XB, 令Y=XB, 將非線性回歸形式轉為線性回歸形式:

計算完每一項SI之后, 本研究將棲息地適宜性指數模型設置為:

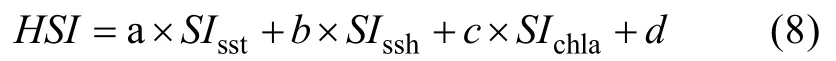
SI是單項棲息地適宜性指數,d為回歸方程中的常數項。根據每個月不同的環境數據和棲息地適宜性指數數據, 利用回歸方程(8)計算出參數a、b、c和d即可得到每個月的綜合棲息地適宜性指數模型。

2 實驗過程與實驗結果

2.1 實驗過程

本研究的整個實驗流程見圖3, 在數據預處理部分加入空間自回歸對缺失數據進行補全; 然后利用空間聚類對補全后的數據進行漁區劃分; 再對每個漁區分別建立棲息地適宜性指數模型; 最后通過捕撈點的地理位置和環境信息, 確定該點所屬漁區,結合該漁區的預測模型對該點產量進行預測, 并與真實數據對比, 從而驗證該模型。

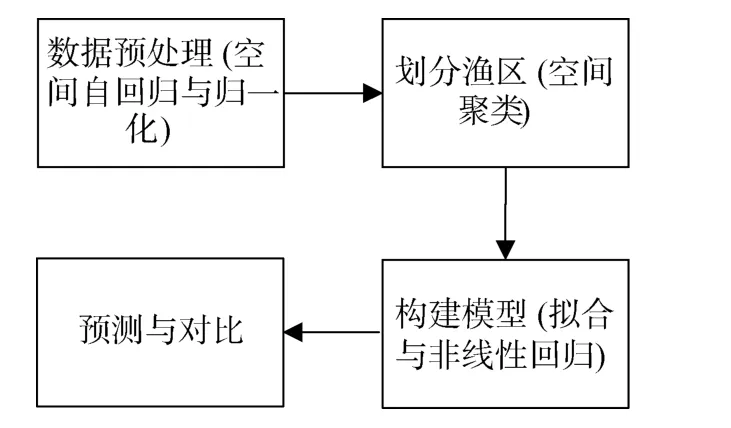
圖3 實驗流程及對應方法Fig.3 Experimental process and corresponding methods

利用2005年1月～2010年12月印度洋大眼金槍魚的數據進行建模。首先, 根據本研究提出的空間自回歸對缺損的數據進行補全。從IOTC官方網站下載印度洋 40°S～15°N, 40°E～120°E 區域內大眼金槍魚漁獲數據。根據文獻[13]中顯示, 印度洋大眼金槍魚除45°S以上的高緯度區域之外均有產量。但獲取的作業數據中, 許多地理位置沒有記錄相應的產量數據。通過選取產量不為零的數據作為建立模型的數據集, 對產量的空間缺失值進行插補, 擴充后續建模數據樣本。

以 2009年 1月數據為例, 先對東經取正值, 西經取負值, 北緯取 90-緯度值, 南緯取 90+緯度值,對環境數據進行歸一化, 與漁業作業數據進行匹配即可獲得適合后續聚類、回歸的數據樣本。表1為2009年1月經過組織之后的數據樣本。

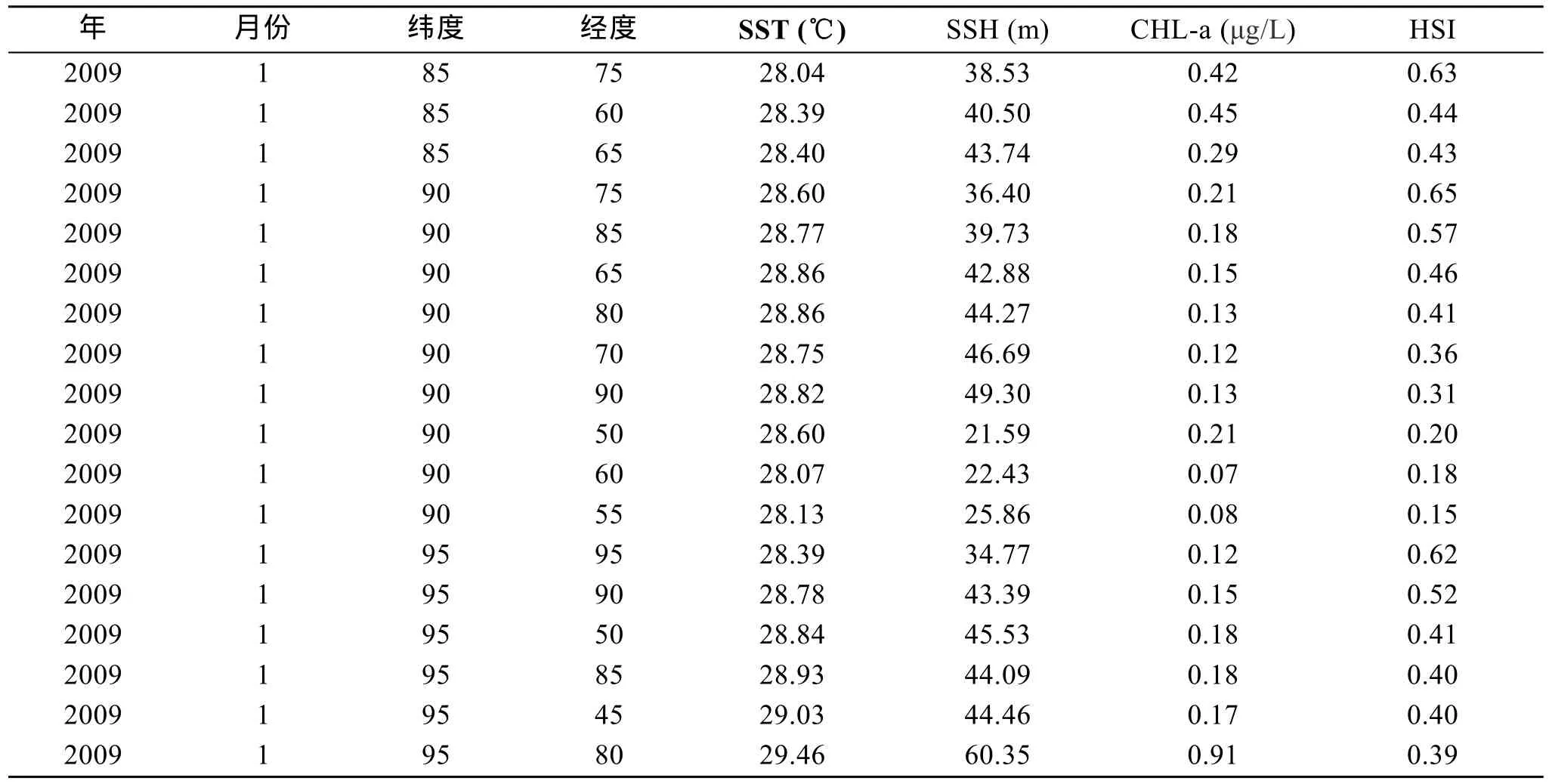
表1 2009年1月數據樣本(部分)Tab.1 Data sample in Jan 2009(partial)

然后根據算法1, 得到聚類結果。聚類數量根據實際應用而定, 它的值會直接影響最終聚類結果,在實際應用中K值通常取為2～5。因此, 本研究將K分別設置為2、3、4、5, 利用Matlab2012b進行仿真實驗。根據不同K值對數據進行聚類, 得到所有數據點歸屬類別后, 逐類別進行相關系數計算, 設xi=(xi1,xi2,...,xip)和xj=(xj1,xj2,...,xjp)是第i個和j個數據點觀測值, 兩個數據點之間相關系數為:

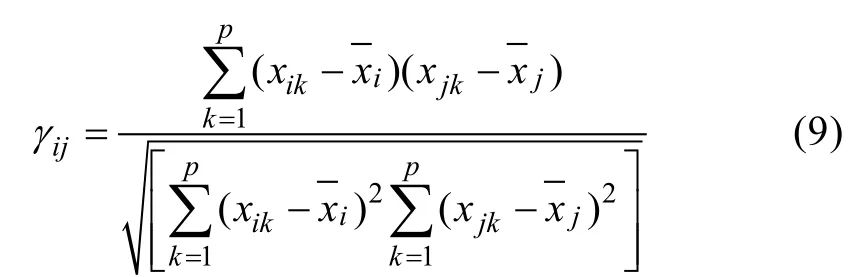
總體相關系數為:

通過算術平均方法得到不同K值下的相關系數,表2為相關系數計算結果。

表2 K取不同數值的相關系數Tab.2 Correlation coefficients of different K values

根據計算結果, 當K=3時, 得到的相關系數最大。因此, 本研究將K值確定為3。

在K均值算法中, 聚類重心的確定對后續聚類結果有很大影響。由于聚類的目的是找到地理位置上相對集中的幾個區域, 從而減少回歸的誤差,而聚類的指標是以距離為度量值, 因此, 本研究通過均勻劃分經緯度選取初始聚類重心。由于研究區域為印度洋 40°S～15°N, 40°E～120°E, 其經向范圍較緯向范圍大, 因此, 本研究以赤道 0°為緯度基線, 以此基線平分經度跨度, 東經取正值, 西經取負值, 北緯取 90-緯度值, 南緯取 90+緯度值,則初始中心的坐標以經緯度表示約為(0, 54), (0, 80)和(0, 106)。

令閾值為0.5, 將最終聚類迭代次數限定為1000次, 利用前文提出的空間聚類算法, 以表1的數據為例根據經緯度數據以及HSI數據, 對2009年1月份聚類結束后, 經過組織得到表3。

表3 2009年1月數據聚類結果(部分)Tab.3 Results of data clustering in Jan 2009 (partial)

根據2005年1月至2010年12月的聚類結果, 類別 1為赤道～35°S、80°E～110°E 的東印度洋區域; 類別 2 為 10°N～10°S、50°E～85°E 熱帶印度洋區域; 類別 3 為赤道～35°S、30°E～55°E 的西印度洋區域。

將2005年1月～2010年12月每一個月的數據進行聚類, 然后對所有數據進行類別標號。選取 2005年1月～2010年12月的金槍魚延繩釣產量數據和相關海洋環境因子作為建模數據。對每一個環境因子和產量分別作非線性擬合, 將最佳擬合公式作為棲息地適宜性指數計算公式中的單項 SI, 再利用公式(8)計算出參數a、b、c和d即可得到每個月的綜合棲息地適宜性指數模型。

2.2 實驗結果

本研究通過聚類過程發現: 當海表溫度在 26℃～29℃, 葉綠素濃度在(0.1～0.3)mg/m3, 海面高度較高時, 棲息地適宜性指數較高, 這與文獻[13, 22～24]中的表述一致。

本研究以2005年至2010年的1月份數據為例,將棲息地適宜性指數大于 0.4的網格點在地圖上標出, 結果發現: 印度洋大眼金槍魚延繩釣的產量分布面較廣, 除 45°S以上的高緯度海域外, 幾乎整個印度洋海域, 均有其產量分布; 主要漁場集中在10°N～20°S, 50°E～85°E 的海域; 高產漁區以西印度洋為主; 東印度洋也有分布, 但產量明顯稀少。以上均與文獻[13]和文獻[25]中吻合。

由于在構建棲息地適宜性指數模型之前對數據進行了空間聚類, 將地理位置相對較近而且棲息地適宜性指數與環境因子相關性較高的數據樣本聚集到一起, 因此在模型檢驗及后續預測中心漁場中,需要根據數據樣本到每個聚類重心的距離選取棲息地適宜性指數模型。

本研究采用 2011年 1～12月的數據對模型進行驗證。針對每月數據, 根據每條記錄對應的經緯度,計算其到3個聚類重心的距離, 確定其所屬類別。再將該記錄的環境數據代入相應的棲息地適宜性指數模型, 得到對應的棲息地適宜性指數估計值。最后在同一張圖中對比預測值與真實值得到圖4。

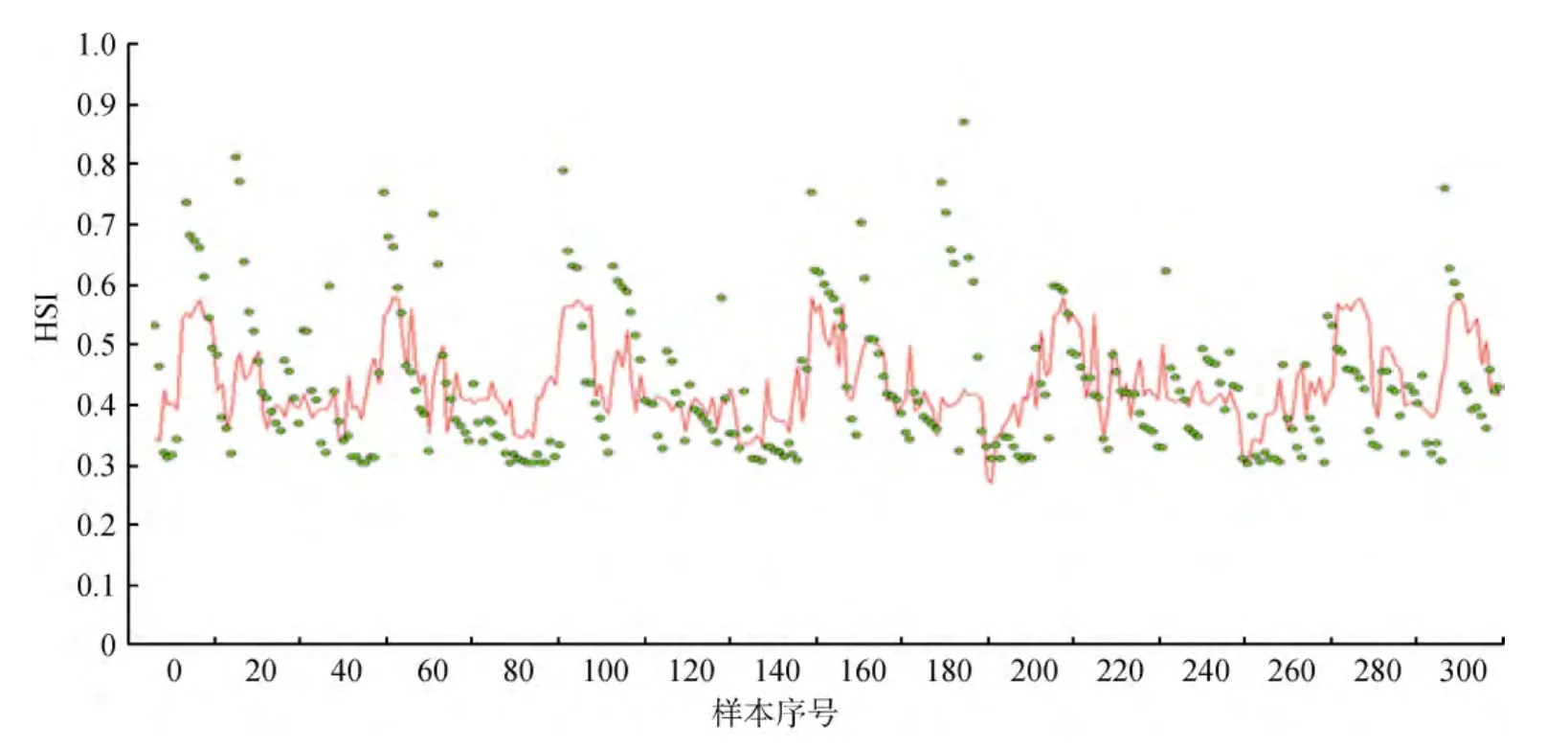
圖4 預測與真實數據比較Fig.4 Comparison of predicted and actual data

在圖4中橫坐標表示每組數據的序號, 圓點是實際HSI值, 折線為預測模型得到的HSI值, 由圖可知真實HSI最高值接近1.0, 但多數集中在0.4～0.6, 而預測值最高約為0.5, 且出現頻率較高, 與事實符合。

3 討論與結論

得到每個月的棲息地適宜性指數估計值之后, 計算其均方誤差(MSE), 圖5為本研究提出的基于空間聚類的漁情預測方法(Spatial Clustering Based Fishery Forecasting, SCBFF)和傳統線性回歸方法的誤差對比。

由圖5可知, 本研究提出的方法要優于傳統的線性回歸方法, 這是因為傳統的線性回歸預測方法并未考慮到因為數據缺失而導致預測精度偏低的問題, 作者通過空間自回歸模型補全數據, 從數據本身的角度出發, 為之后的預測奠定了良好的基礎。此外傳統的預測方法是直接對整個漁區進行建模預測,并未考慮不同地理位置或不同環境所引起的偏差,作者充分考慮該偏差所引起的預測誤差較大的問題,根據環境數據隨著地理位置變化而變化的特點, 采用基于空間聚類的漁區劃分方法, 將漁獲量之間相關性較高并且相對地理位置較近的數據, 聚集在同一個類中, 對每個漁區分別建立模型, 有效地提高了預測精度。

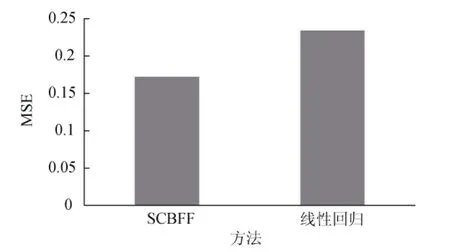
圖5 SCBFF與線性回歸的均方誤差比較Fig.5 Comparison of MSE between SCBFF and linear regression

由于環境數據采集困難, 本研究僅從海表溫度、海面高度和葉綠素濃度等 3個方面考慮海洋環境因子對金槍魚產量的影響, 但實際上還有許多影響印度洋金槍魚分布的因素, 包括海水鹽度、餌料生物分布等環境因子, 這為本課題的后續研究提供空間。同時, 本研究能夠根據現有的 3種環境因子與棲息地適宜性指數之間的關系構建出棲息地適宜性指數模型, 且平均預測性能良好, 但對于部分極值, 如棲息地適宜性指數非常高的區域并不能很好地預測出來,這也將成為后期深入研究方向之一。

本研究針對傳統漁情預報方法由于精度偏低的問題, 利用空間自回歸、K均值空間聚類、非線性回歸等技術的優點, 提出一種基于空間自回歸和空間聚類的漁情預報模型。首先, 利用空間自回歸根據空間位置插補數據的能力, 插補缺損數據, 從而補全數據。再利用基于空間聚類的漁區劃分方法, 對漁區進行劃分。最后根據每一類中環境數據和產量數據之間的數學關系, 通過函數擬合與非線性回歸分析,得到每個不同漁區塊各自的棲息地適宜性指數模型。通過與傳統的金槍魚預測方法進行對比試驗, 實驗結果表明, 在提高模型擬合程度和減小預測誤差方面, 本方法要優于傳統的漁情預報方法。

[1] 沈金鰲, 方瑞生.浙江近海冬汛帶魚漁獲量預報方法的探討[J].水產科技情報, 1982, 5: 1-5.

[2] 陳新軍, 鄭波, 李綱.GLM和GAM模型研究東黃海鮐資源漁場與環境因子的關系[J].水產學報, 2008,32(3): 379-386.

[3] 陳新軍.西北太平洋柔魚漁場與水溫因子的關系[J].上海海洋大學學報, 1995, 3: 181-185.

[4] 陳新軍, 田思泉, 錢衛國.月相對北太平洋海域柔魚釣獲率的影響[J].海洋漁業, 2006, 28 (2): 136-140.

[5] 杜云艷, 周成虎, 崔海燕, 等.遙感與 GIS支持下的海洋漁業空間分布研究——以東海為例[J].海洋學報, 2002, 24(5): 57-63.

[6] 袁紅春, 顧怡婷, 汪金濤, 等.西北太平洋柔魚中長期預測方法研究[J].海洋科學, 2013, 37(10): 65-70.

[7] 張月霞, 丘仲鋒, 伍玉梅, 等.基于案例推理的東海區鮐魚中心漁場預報[J].海洋科學, 2009, 33(6): 8-11.

[8] Masahiko M, Yasuaki T.Vertical distribution and optimum temperature of bigeye tuna in the eastern tropical India Ocean based on deep tuna longline catches[J].Journal of National Fisheries University, 1997, 46(1):13-20.

[9] Mohri M, Hanamoto E, Takeuchi S.Optimum water temperatures for bigeye tuna in the Indian Ocean as seen from tuna longline catches[J].Nippon Suisan Gakkaishi, 1996, 62: 761-764.

[10] Daniel G, Francis M.Comparative analysis of the exploitation of bigeye tuna in the Indian and eastern Atlantic oceans with emphasis on purse seine[R].Victoria:IOTC Proceedings, 1999, 2: 158-171.

[11] Hiroaki O, Naozumi M, Takayuki M.GLM analyses for standardization of Japanese longline cpue for bigeye tuna in the indian ocean applying environmental factors[R].Japan: IOTC Proceedings, 2001.

[12] Menard F, Marsac F, Bellier B, et al.Climatic oscillations and tuna catch rates in the Indian Ocean: a wavelet approach to time series analysis[J].Fisheries Oceanography, 2007, 16(1): 95-104.

[13] 苗振清, 黃錫昌.遠洋金槍魚漁業[M].上海: 上海科學技術文獻出版社, 2003: 24-26.

[14] 李軍, 李志凌, 葉振江.大眼金槍魚漁業現狀和生物學研究進展[J].齊魯漁業, 2005, 22(12): 35-38.

[15] Herrera M L, Pierre M J.Review of the statistical data available for the tropical tuna species[R].Maldives: Indian Ocean Tuna Commission, 2011.

[16] Lin C R, Liu K H, Chen M S.Dual clustering: integrating data clustering over optimization and constraint domains[J].IEEE Transactions on Knowledge and Data Engineering, 2005, 17(5): 628-637.

[17] Zhou J G, Guan J H, Li PX.A Dual clustering algorithm for distributed spatial databases[J].Geo2spatial Information Science, 2007, 10(2): 137-144.

[18] 柳盛, 吉根林.空間聚類技術研究綜述[J].南京師范大學學報(工程技術版), 2010, 10 (2): 57-62.

[19] 王家樵, 朱國平, 許柳雄.基于 HSI模型的印度洋大眼金槍魚棲息地研究[J].海洋環境科學, 2009, 28(6):739-742.

[20] 陳新軍, 馮波, 許柳雄.印度洋大眼金槍魚棲息地指數研究及其比較[J].中國水產科學, 2008, 15(2):269-278.

[21] 胡振明.利用棲息地適宜指數分析秘魯外海莖柔魚漁場分布[D].上海: 上海海洋大學, 2009.

[22] 楊勝龍, 張禹, 樊偉, 等.熱帶印度洋大眼金槍魚漁場時空分布與溫躍層關系[J].中國水產科學, 2012,19(4): 679-689.

[23] 曹曉怡, 周為峰, 樊偉, 等.印度洋大眼金槍魚、黃鰭金槍魚延繩釣漁場重心變化分析[J].上海海洋大學學報, 2009, 18(4): 466-471.

[24] 陳雪冬, 崔雪森.衛星遙感在中東太平洋大眼金槍魚漁場與環境關系的應用研究[J].遙感信息, 2006, 1:25-28.

[25] 楊勝龍, 馬軍杰, 伍玉梅, 等.印度洋大眼金槍魚和黃鰭金槍魚漁場水溫垂直結構的季節變化[J].海洋科學, 2012, 36(7): 97-103.