某型航空發動機的溫度傳感器慣性補償研究*

王立國， 鄧羅泉， 劉卓崴， 鄭鐵軍， 程 禮

(空軍工程大學 航空航天工程學院，陜西 西安710038)

某型航空發動機的溫度傳感器慣性補償研究*

王立國， 鄧羅泉， 劉卓崴， 鄭鐵軍， 程 禮

(空軍工程大學 航空航天工程學院，陜西 西安710038)

針對某型航空發動機溫度傳感器的測量滯后問題，提出了傳感器的慣性補償方法。該方法首先求得時間常數，并采用最小誤差原則對時間常數進行修正，然后將時間常數寫入補償環節，最后使用二次指數平滑法對補償曲線進行修正。通過仿真與實驗驗證，求出了時間常數并實現了溫度補償，表明該方法是有效的，能夠用于溫度傳感器的慣性補償。

傳感器； 慣性補償； 時間常數； 時間序列

0 引 言

航空發動機渦輪后燃氣溫度T6是表征發動機工作狀態的重要參數[1]，需要準確地測量。而測量T6的溫度傳感器是由物理元器件構成，由于材料屬性與結構的限制，無法瞬間完成熱能交換[2],這就導致了測量值的滯后，影響發動機燃氣溫度控制系統的正常工作，因此，需要對溫度傳感器進行慣性補償。程建華[3]設計的軟件補償和濾波的方法能夠定期為測溫回路進行測定補償，但主要適用于恒溫系統，不能滿足發動機要求；夏敦柱[4]提出了使用神經網絡進行傳感器補償的方法，但神經網絡計算量大，對樣本數據質量、數量的依賴程度高，應用實例與網絡規模易產生矛盾等。

為更好地實現溫度補償，某型航空發動機的控制系統中使用了一部分補償電路,但有很多關鍵性技術有待研究解決，比如：時間常數和如何實現溫度補償等。

本文主要在分析硬件電路基礎上，驗證了溫度補償原理的實現過程，并提出了時間常數的求取方法和傳感器數據的處理方法。按照最小誤差原則對求時間常數做了創新性工作，并嘗試使用時間序列法解決補償不理想問題。各種方法應用的效果已通過仿真和實驗驗證。

1 補償電路原理

溫度補償裝置原理結構圖如圖1所示。

圖1 溫度補償裝置圖

該裝置補償思路是將傳感器輸出的滯后溫度T6輸入到一個傳遞函數為τs+1的補償環節，使補償環節輸出的溫度與輸入的溫度相同，如圖2所示。

圖2 溫度補償流程圖

其中，T6為渦輪后燃氣溫度，τ為溫度傳感器時間常數。

2 時間常數的獲得

本文對比了幾種常用慣性環節時間常數的求取方法，從中選取適于渦輪后燃氣溫度測量的一種。

2.1 溫度傳感器一階慣性模型

假設傳感器內部溫度分布均勻、沒有輻射換熱并忽略導熱，考慮發動機溫度傳感器安裝的保護套，由文獻[5]知傳感器模型為二階慣性模型，可以直接使用簡單的一階慣性模型來代替。雖然一階模型缺少二階模型的某些特征或有其他缺陷[6]，但對于發動機控制系統的溫度補償是無關參數，因此，傳感器模型如公式(1)所示

(1)

式中Ts，Tm分別為傳感器與介質溫度，τ為傳感器敏感體與保護套共同的時間常數。

2.2 求取時間常數

2.2.1 定義法

由一階系統階躍響應曲線知，響應值從初始值上升到終值的63.2 %所用時間,即為階躍響應的時間常數

τ=0.632Tm.

(2)

仿真數據中一般沒有準確的響應值，故先對數據進行拉格朗日插值，再求時間常數。

2.2.2 溫度變化法

根據溫度傳感器的慣性模型公式(1)，得通解為

Ts=C′e-t/τ+Tm.

(3)

可導出τ的公式

(4)

式(4)表明:只要知道Tm-Ts，就可求出時間常數τ。

2.2.3 斜率法

對式(1)移項，可得

τ=(Tm-Ts)/(dTs/dt).

(5)

表明只要得到曲線斜率，即可得到時間常數τ。

2.3 時間常數仿真實驗

利用Matlab軟件構建一階慣性系統，取單位階躍量和幾組合適的時間常數，驗證三種方法的有效性。

表1中的實驗數據表明:經拉格朗日插值的定義法和溫度變化法在時間常數為0.9～8的范圍沒有誤差，斜率法計算時認為相鄰數據按照直線變化，而實際曲線按指數規律變化，導致誤差的出現。由于時間常數會隨著外界條件如溫度的變化而變化，而溫度變化法可以實現對求得的時間常數進行實時修正，因此，本文將溫度變化法作為求取慣性時間常數的方法。

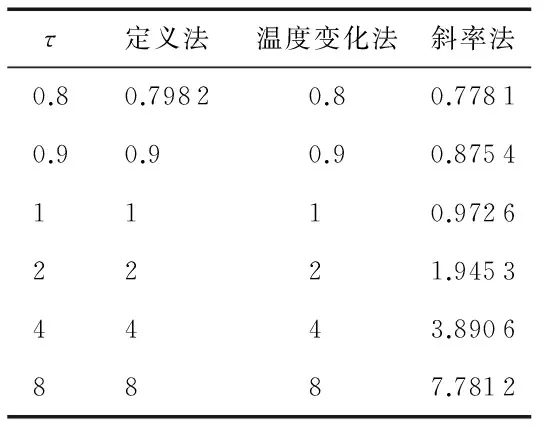
表1 時間常數仿真結果對照表

3 實驗驗證

利用仿真求得時間常數，在Matlab上能容易地得到理想的補償曲線，這里不再贅述。利用搭建的實驗平臺，對溫度傳感器慣性補償方法進行了實驗驗證。由于補償方法具有通用性，因此，實驗中未選擇某型航空發動機測量排氣溫度的熱電偶，而是使用了溫度易于獲取的數字化溫度傳感器DS18B20，該傳感器體積小，可實現高精度測溫，時間常數約在1～5 s之間，適用于本實驗需要。表1數據表明：使用溫度變化法可以準確得到DS18B20的時間常數。

3.1 實驗平臺描述

以Atmel公司的89C51單片機為控制器，實驗平臺如圖3所示。第一次測量溫度屬于系統學習過程，從第二次測量開始為帶有補償溫度的輸出。

圖3 實驗裝置連接圖

將傳感器從室溫21 ℃迅速放入83 ℃熱水中，測得實驗數據[7]，如圖4中曲線所示。

圖4 DS18B20階躍響應曲線

從圖4中可以看出:實際測得的曲線有波動，在計算時間常數時必然會出現誤差，比如在A點求得的時間常數為負值，因此，需要先對曲線進行平滑處理。

3.2 求取時間常數與補償溫度

最小二乘法是通過最小化誤差的平方和尋找數據的最佳函數匹配的數學優化技術。可用于參數估計與曲線擬合[8]。本文利用最小二乘法對實驗數據進行擬合，擬合曲線如圖5所示，可以看出：比較理想的范圍是2～6次，從第5次擬合開始曲線出現大的波動，3次擬合的階躍上升部分高于其它階次曲線，2次擬合則偏低，所以，溫度數據擬合選為4次。

圖5 2～6階最小二乘擬合的曲線

從擬合的曲線上按照0.05 s時間間隔讀取數據，采用溫度變化法求出時間常數。為得到實時準確的時間常數，以最小誤差為原則對時間常數進行修正

(6)

式中 τ′為第t次校正后的時間常數，τ為第t次計算的時間常數，ζ為修正系數， error(t-1)-t為第t-1次與第t次時間常數差值。

經計算發現，時間常數主要在τ=1.83附近浮動，且呈不明顯的變大趨勢，表明該方法是有效的。

將時間常數寫入補償環節，繪制仿真曲線如圖6所示。

由圖6可以看出:曲線波動幅度很大，效果不理想，沒起到溫度補償作用。分析原因：一是傳感器測量的不準確性，比如：在t=τ時刻傳感器輸出值不一定是階躍值的63.2 %，可能偏大或者偏小；二是本文把傳感器二階慣性模型建立為一階慣性模型，導致使用的一階慣性補償策略對實際的二階模型并不適用，出現了過補償或欠補償的現象,所以，還需進一步對補償工作進行改善。

3.3 補償曲線的校正

時間序列法是通過對預測目標時間序列的處理來研究其變化趨勢的。眾多學者已經將它引入工程實踐中[9]，并取得了良好效果。

本文根據補償溫度時間序列應呈直線趨勢的特點，將移動平均公式改進為一次指數平滑公式，然后在一次指數平滑基礎上，利用滯后偏差規律建立直線趨勢模型，作二次指數平滑

(7)

(8)

(9)

其中

(10)

由于實測溫度數據也會存在誤差，導致由數據求得的系數有誤差，為避免此問題，在采集到數據后對各系數利用公式(11)進行修正

(11)

式中 λj(j=1,2)為調整常數，實驗經多次調整，選定λ1=0.03，λ2=0.02為最佳參數，ei+1為第t+1實測溫度與預測溫度的預測誤差。這樣當系統a,b的選擇偏大時，誤差ei+1為負值，可以調小系數;反之,亦然。歷史觀測值個數為20，此方法得到的響應曲線如圖7所示。

圖7 時間序列法整理的曲線

從圖7中可看出:補償過后的調節時間比補償前縮短約5s，約占原調節時間的65.7 %，效果比較理想。故認為在補償環節用時間序列法處理后的數據是可行的，能夠實現實時地補償溫度。

4 結 論

本文某型航空發動機渦輪后燃氣溫度補償的實際問題出發，解決了如何求得時間常數和實現溫度補償的問題,并得出如下結論：

1)在不考慮外界條件對時間常數影響的前提下，使用溫度變化法能夠較為準確地求得溫度傳感器的時間常數。

2)針對時間常數隨外界因素變化而變化的情況，按照時間常數修正公式能夠有效地進行實時修正。

3)對于補償實驗中出現的補償曲線大幅度波動問題，可采用了基于時間序列的二次指數平滑法，同時對平滑公式系數進行校正來解決。

本文所提出的方法具有一般適用性和參考性，可應用于流量、壓力等其他形式的慣性系統。

[1] 王海濤,謝壽生,胡金海，等.基于Volterra-Laguerre拓展模型的發動機加速過程辨識[J].航空動力學報,2009,24(2):465-469.

[2] Tian Feifei,Cong Jiawei,Yun Binfeng，et al.A fiber Bragg grating current sensor with temperature compensation[J].Optoelectronics Letters,2009,5(5):347-351.

[3] 程建華，羅立成，王鑫哲.高精度測溫系統的測溫補償算法研究[J].傳感器與微系統,2010,29(11):36-39.

[4] Xia Dunzhu,Wang Shourong,Zhou Bailing.Temperature compensation method of silicon microgyroscope based on BP neural network[J].Journal of Southeast University:English Edition,2010,26(1):58-61.

[5] 鹿曉力,路立平,李 奎，等.溫度傳感器動態特性完全補償方法研究與補償電路設計[J].鄭州大學學報:工學版,2012,33(3):65-70.

[6] Shi Jian,Zhang Shuyou.Model order reduction for coupled dynamic characterization of torsional micromirrors[J].Chinese Journal of Mechanical Engineering,2011,24(5):829-835.

[7] 劉宗瑞，咸婉婷，劉志遠.熱電偶動態響應測試系統[J].傳感器與微系統,2014,33(6):82-85.

[8] Yu Shengwen,Dong Jun,Wang Aimin.Least squares fitting of coordinate paramaters model[J].Trans on Nonferrous Met Soc China,2005,15(1):189-191.

[9] Hu Liang,Che Xilong.Parameter selection in time series prediction based on nu-support vector regression[J].High Technology Letters,2009,15(4):337-342.

Inertial compensation study of temperature sensor in aeroengine*

WANG Li-guo, DENG Luo-quan, LIU Zhuo-wei, ZHENG Tie-jun, CHENG Li

(College of Aeronautics and Astronautics Engineering,Air Force Engineering University, Xi’an 710038,China)

Aiming at problem of measurement hysteresis of temperature sensor in a type of aeroengine,a method for inertial compensation of sensor is proposed.This method firstly gets time constant,and advice it adopt least error rule;then applys time constant to compensate;finally,secondary exponential smoothing method is used to revise the compensation curve.By simlation and experimental verification,time constant is obtained and temperature compensation is realized,and it shows that the method is effective and it can be used for inertial compensation of temperature sensor.

sensor; inertial compensation; time constant; time series

10.13873/J.1000—9787(2015)03—0066—03

2014—12—17

國家自然科學基金面上項目(51175509)

TH 81

A

1000—9787(2015)03—0066—03

王立國(1989-),男，吉林省長春人，碩士研究生，研究方向為航空宇航科學與技術、航空發動機控制。