Micromine在云南芒市金礦三維建模及資源量估算中的應用
時昆林,馮文杰
(1.云南弘迪礦產資源有限公司,昆明650051;2.云南省地質調查院,昆明650051)
芒市金礦位于岡瓦納古陸和歐亞古陸塊碰撞接合部的三江地質構造轉換帶南西緣,龍陵-瑞麗大斷裂南東側,上芒崗地壘西北翼的次級斷裂帶中,受上芒崗斷裂控制,處于成礦非常有利的地壘邊沿的構造復合部位[1-3]。
礦區出露的地層主要有下二疊統沙子坡組和中侏羅統勐戛組(圖1)。沙子坡組(P1s)為白云巖、灰質白云巖夾灰巖及泥砂巖;勐戛組(J2m)為紫紅色細砂-粉砂巖與泥硅質灰巖。金礦體賦存于J2m中,受上芒崗斷裂(F1)控制,呈厚板狀或似層狀產出,走向北東,傾向北西,為微細粒浸染型金礦。
2014年對芒市金礦麥窩壩礦段進行了工程勘探(圖1),其中鉆孔48個,撥土7條,共計1 891件化學樣,并按《巖金礦地質勘查規范》(DZ/T 0205—2002)要求,將芒市金礦資源儲量估算的工業指標和礦體圈定類型分別確定參數,詳見表1。
近年來礦業軟件在礦產儲量評價中得到了較為廣泛的應用[4-8],本文根據芒市金礦麥窩壩礦段的原始數據,在Micromine軟件內建立地形數據、鉆孔數據、化學樣數據,通過Micromine普通克里格方法估算該礦區資源量。
1 Micromine礦體解譯與建模[4,8]
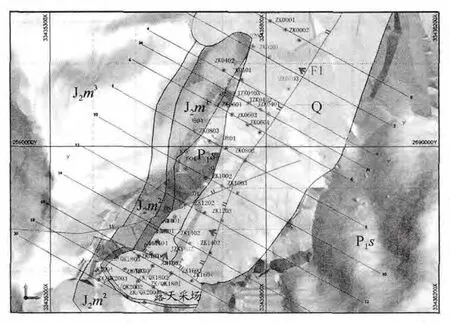
圖1 芒市金礦麥窩壩礦段地質及工程分布平面模型Fig.1 Geology and engineering distribution of Maiwoba ore section,Mangshi gold

表1 礦床參數與礦體圈定類型Table 1 Deposit parameters and orebody delineation type
通過Micromine三維地質勘探軟件估算芒市金礦資源儲量,為使其結果能與傳統方法的估算具有可比性,Micromine解譯礦體剖面時采用與地質勘探儲量估算的剖面一致,且按相同原則在單、多工程基礎上(樣品達到邊界品位Au 0.3 g/t和厚度>1 m)圈定,結合礦體空間分布、產出位置和多工程三度空間上的對應關系,沿勘探線工程解譯每條剖面,連接高出邊界品位對應的點與線,并按規范外推形成礦體剖面輪廓線。礦體圈定原則綜合考慮了礦床地質特征、礦石選冶性能以及礦山開采成本等多方面因素,同時也對夾石作了圈連,并在建模時對夾石進行了自然剔除(圖2)。
在計算資源量時,礦體中的夾石被剔除,其結果更為客觀,計算的資源量也更真實,因此Micromine估算金礦儲量比傳統估算方法更精確、更可靠、更科學。
當同一工程中有多層礦體時(圖2),按礦體的總體產狀分別連接不同的礦體,最終建立礦區I—Ⅺ號礦體的實體模型(圖3),并按2 m×2 m×1 m(北×東×高)的立方體劃分這些礦塊,并將樣品組合數據賦予這些礦塊,最終建立該礦區的礦體數據模型。
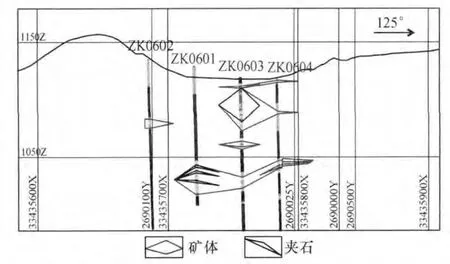
圖2 麥窩壩礦段6號勘探線剖面圖Fig.2 Profile of No.6 exploration line in Maiwoba ore section
2 樣品數據預處理
化學樣品預處理的目的是了解化學樣本中是否存在特高品位值。在計算資源量中特高品位值會拉高礦體平均品位而影響資源量大小,使之偏離正確的資源量估算結果。Micromine從統計學觀點出發,在樣本數足夠多的條件下,其樣本都遵從正態分布,并在正態分布紙上繪制累積頻率曲線圖以了解樣本的連續特性,從而求出樣本的特高品位。
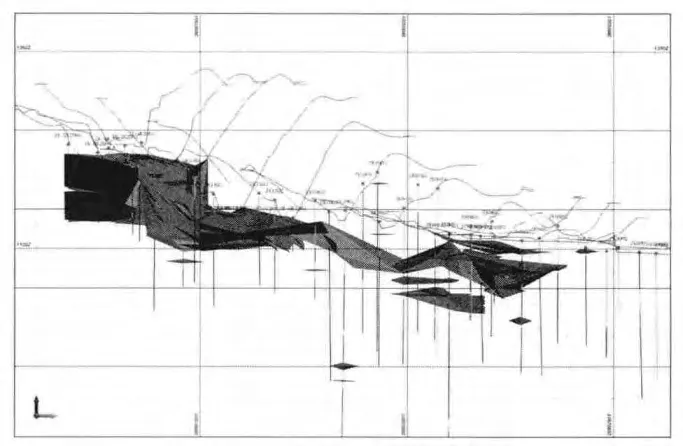
圖3 麥窩壩礦段礦體縱向剖面圖Fig.3 Longitudinal section of orebody in Maiwoba ore section
2.1 化學樣品統計分析
本礦區選取礦體內共計1 924個(含樣品間隔33個)化學樣,根據Au的品位數據,在正態概率紙上作累積頻率曲線圖,結果見圖4。Au元素的品位累積頻率曲線總體上是條直線。在直線上部,18.1×10-6以上存在少量離散點,且偏離直線方向,表明存在特高品位。經核實屬非人為因素或測試誤差所致。用Micromine查找鉆孔特高品位(表2),將其用上截品位值18.1×10-6替換。替換后各參數有所下降,品位分布較為穩定(表3)。
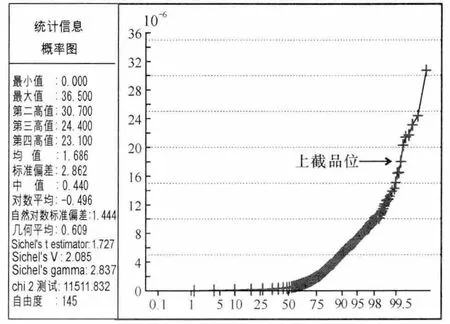
圖4 Au品位累積頻率曲線及上截品位圖Fig.4 Cumulative frequency curve of Au grade and upper cut-off grade of ore
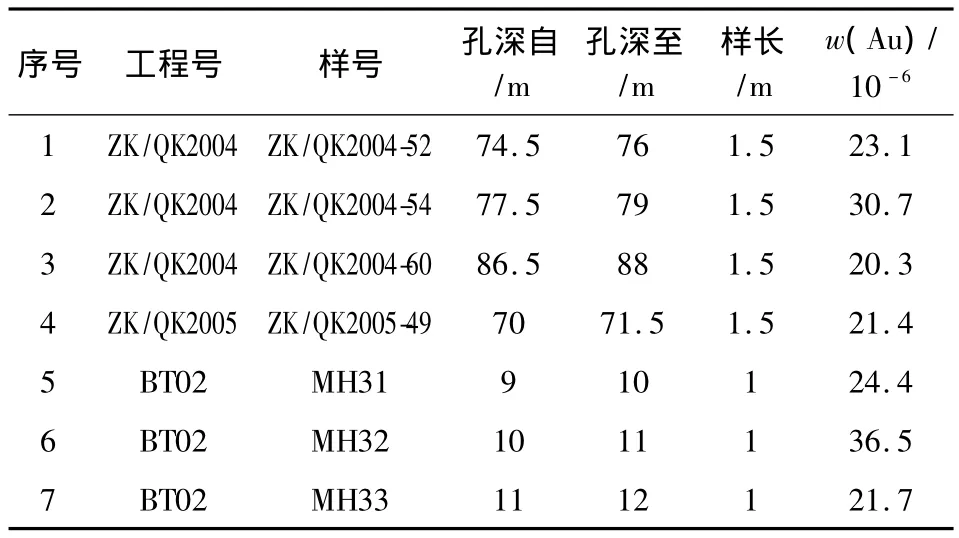
表2 特高品位值及工程位置Table 2 Special high-grade values and engineering positions
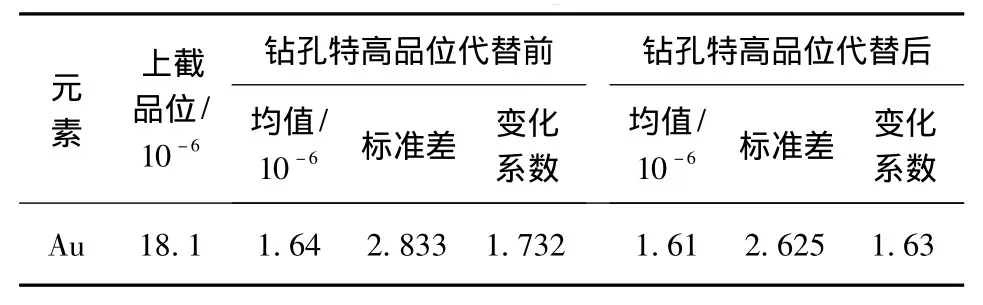
表3 品位特高值處理前后統計分析Table 3 Statistical analysis of special high sample grade before and after replacement
2.2 樣品組合及組合樣統計分析
Micromine在利用地質統計學方法進行資源量估算時,需要處理所有參與插值的樣品值,使之具有相同的樣長。經Micromine統計,芒市金礦麥窩壩礦段化學樣的樣長多為1或1.5 m。由于實際取樣長度60%以上為1 m,即取1 m長度作為組合樣長。一方面可把夾石剔除,另一方面可把小范圍內(大于1 m)的變異也反映出來。通過對組合后樣品的統計分析得到6 307個組合樣。從表4中可以看出,Au元素品位變化系數不大,表明金礦體礦化穩定、局部富集的特點。
組合后樣長等于1 m的點數6 268,占總點數的99.38%,滿足樣長穩定。樣品組合后Au品位分布直方圖均近似服從對數正態分布(圖5),表明Au元素品位均為連續型隨機變量,這為元素品位半變異函數的研究提供了條件。
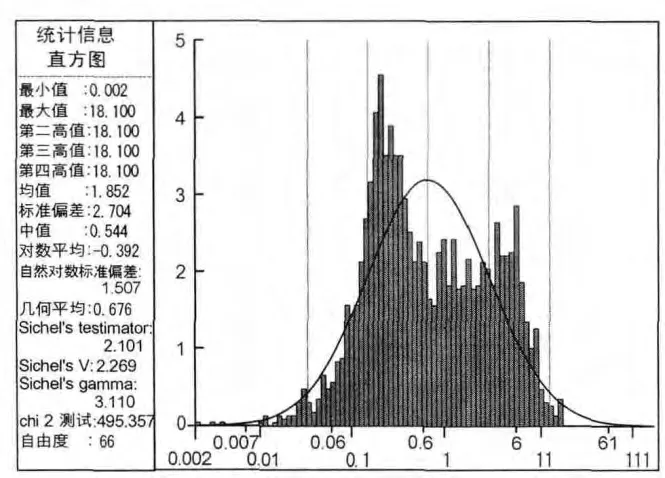
圖5 組合樣中Au元素品位對數分布直方圖Fig.5 Logarithmic distribution histogram of Au elements in combination sample
3 樣品變異函數的擬合
變異函數是當空間點x在一維x軸上變化時,區域化變量在x和x+h處的值Z(x)和Z(x+h)的差的方差之半定義為區域化變量Z(x)在該方向上的變異函數,并記為γ(h)[9]。
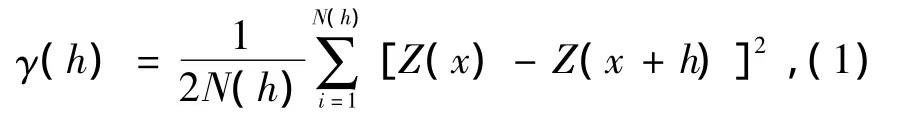
式中:γ(h)—實驗半變異函數;h—步長,即在一定方向上,距離為|h|的矢量;N(h)—步長為h的樣品對數;Z(x)、Z(x+h)—品位的測定值。
式(1)表示,若Z(x)二階平穩假設或內蘊,區域變化量在某個方向的變異函數γ(h)只依賴于Z(x)-Z(x+h)中在某個方向上的h,而與位置無關,則每對預測數據(Z(x),Z(x+h))都可看成是(Z(x)-Z(x+h))的取樣現實。
由于礦體分布具有一定的方向性,區域化變量具有空間各向異性特征。因此,在進行變異函數的計算和分析時將針對不同的方向分別進行。一般情況下,先各向計算相應的變異函數,選取最優變異函數,然后定向計算變異函數,并進行交叉驗證,最終確定出符合礦床特征的變異函數。

表4 組合樣中Au元素統計分析Table 4 Statistical analysis of Au elements in the original sample and combined sample
3.1 求解變異函數
芒市金礦麥窩壩礦段變異函數的求取采用Micromine軟件中圓錐搜索方式對礦區11個礦體的各個方向一定范圍內分布的樣品點進行,選取長度最長、涉及點最多的最優變異函數。通過計算,最后得到了礦區Au元素變異函數的井向(垂向)、主軸(第一方向)、次軸(第二方向)和短軸(第三方向)方向的參數,并根據變異函數球狀模型進行擬合(礦區Au元素模型見圖6~圖9),得到了滯后距、基臺、塊金和變程等參數。
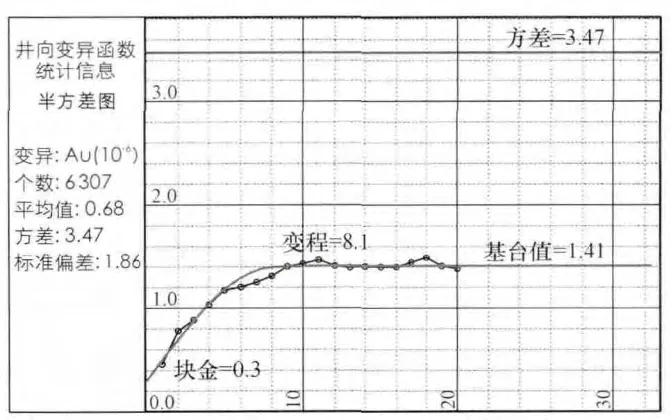
圖6 變異函數球狀模型井向(垂向)擬合Fig.6 Well direction(vertical direction)fitting of spherical model of variation function
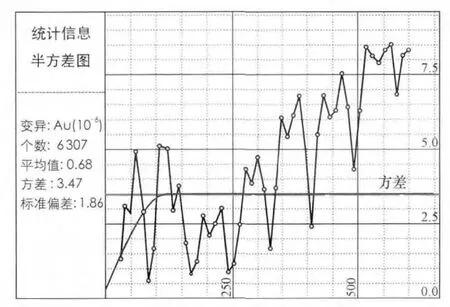
圖7 變異函數球狀模型第一(向下)方向擬合Fig.7 First(downward)direction fitting of spherical model of variation function
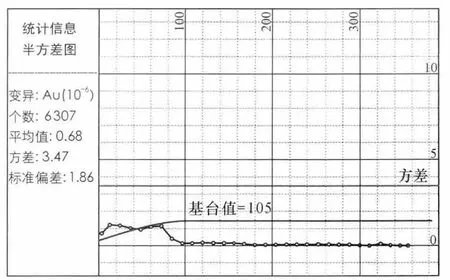
圖8 變異函數球狀模型第二(向下)方向擬合Fig.8 Second(downward)direction fitting of spherical model of variation function
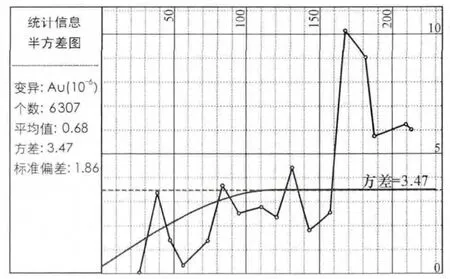
圖9 變異函數球狀模型第三(水平)方向擬合Fig.9 Third(horizontal)direction fitting of spherical model of variation function
從表5可看出,主軸(次軸)方向方位角31°,傾角18°(-72°),正好是礦體的走向和傾伏角的產狀。
3.2 模型檢驗
資源儲量估算要求每一個步驟都十分嚴謹,因此模型檢驗成為對模型合理性把關的重要步驟。模型檢驗分為體積檢驗和交叉驗證檢驗兩步,體積驗證是對模擬出的礦體三維模型礦石量的驗證,交叉驗證是對插值后的品位合理性進行驗證,以確保資源儲量估算結果合理。
3.2.1 體積驗證體積驗證是對礦體實體模型體積與按照采礦要求劃分成若干長方體小塊后的空塊模型的空塊總體積作對比,若體積相差程度在誤差范圍內,則說明此劃分方式下的空塊模型是合理的,空塊模型的合理意味著儲量估算中礦石量的正確。礦體實體模型和空塊模型體積對比見表6。

表5 麥窩壩礦段礦體Au元素變異函數參數Table 5 Variation function parameter of Au element in Maiwoba ore section

表6 礦塊模型體積與礦體總體積對比Table 6 Comparison of ore block model volume and orebody total volume
3.2.2 交叉驗證交叉驗證是對變異函數參數合理性的一種檢驗方法。為了檢驗結構模型以及克里格插值的準確性,采用地質統計學自身完善的交叉驗證方法。利用所得結構模型和已知樣品去估已知值,然后把真實值和估計值進行比較,對兩者的殘差進行統計分析,以判斷變異函數結構的正確性。通過驗證計算芒市金礦麥窩壩礦段礦體中各元素的品位估值,出現殘差的分布為正態分布(圖10),各元素品位實際值與估計值之間的誤差均值趨于零,表明模型確定合理,變異函數參數對元素品位進行估計是無偏的,滿足區域化變量內蘊假設,能用于下一步的儲量計算。
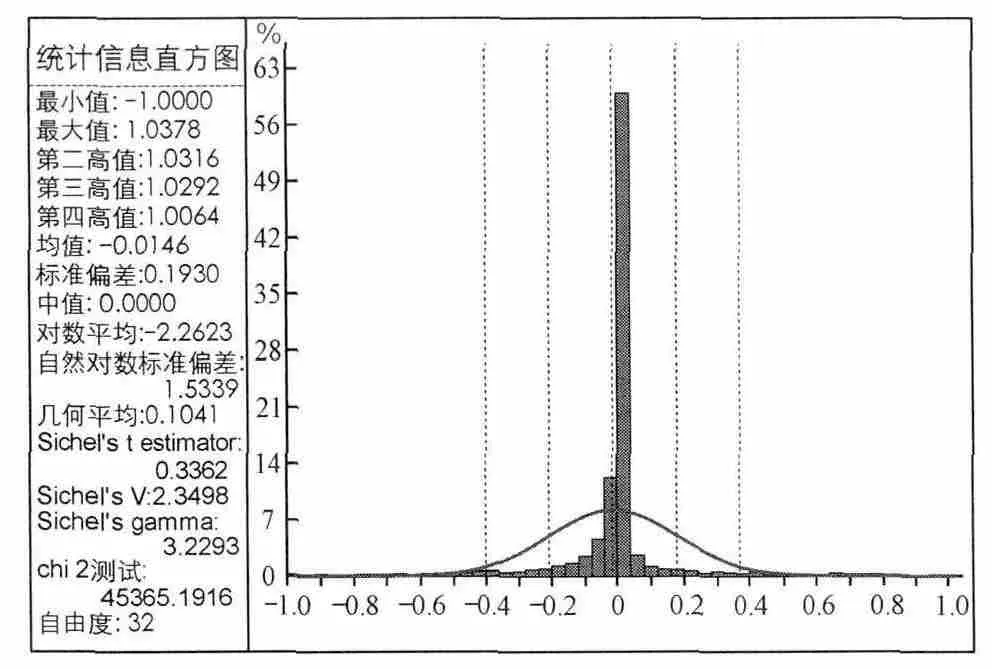
圖10 Au品位交叉檢驗殘差分布直方圖Fig.1 0Residual error histogram of Au grade cross check
4 資源量估算
Micromine估算資源量一般采用距離平方反比法和普通克里格法。
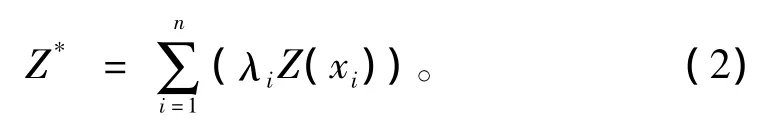
其中:Z*—待估塊段值;λi—與待估點間距成反比的權系數;Z(xi)—樣品實測值。
距離平方反比法是基于樣品空間位置相近則相似原理而提出的估值方法。即越遠離樣品空間位置越不相關,權系數λi越小,也即λi值只與距離有關。該方法考慮到鄰近樣品之間存在著一定的相關關系,并將這種關系簡單地看成是兩者之間距離的函數,其優點是簡便、容易實現。但若采樣出現不均勻的情況下,距離較近、較密點的權值就會較大;且在判定時采用距離的平方、三次方或2/3次方等的主要依據是實踐經驗,樣品品位影響范圍的確定也是經驗數值。因此,距離反比法未考慮樣品的空間結構性和各向異性,只是算術平均法或純幾何的加權法。
普通克立格法是根據一個塊段內若干樣品信息的某特征值(品位),對該塊段特征值作出一種線性、無偏(估值與真實值的數學期望相等),且估計方差最小的插值方法[9-10]。要實現估計方差最小,且無偏,必須滿足下列兩個條件:
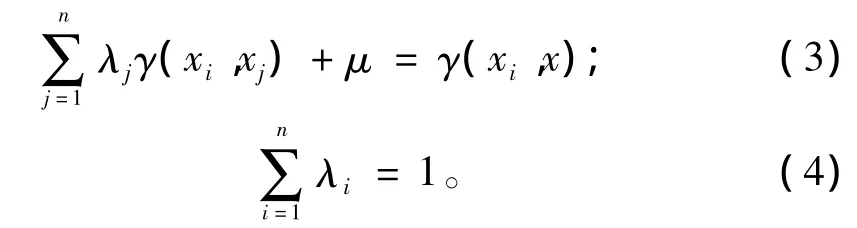
其中,γ—變異函數(見式(1));λi—待估值權系數;xi—塊段估值點;xj—樣品實測值;x—待估值點的空間域;μ—拉格朗日算子。由式(3)、(4)求解出λi,該值與空間變異函數有關;再據式(2)求出待估塊段品位Z*。
由于普通克里格法將“區域化變量”的空間結構性用變異函數來表征,既考慮了樣品空間上的位置關系,又考慮了品位值空間上的差異,理論上證明估計方差最小、無偏,而且具有屏蔽效應。它不會因為樣品不均勻而使權系數λi變大,其結果就是向量空間更加廣泛,投影估值更好,相對于傳統地質塊段法估算有著巨大的優勢;但由于其理論建立在統計學二階平穩的假設上(數學期望值為常數),降低了該方法的堅實性。
因此,本文估算芒市金礦麥窩壩礦段礦體資源量采用普通克立格法和距離平方反比法,兩種方法的結合可互補優缺點,目的是使估算結果更接近真實性。其估算結果見表7。
普通克立格法估算麥窩壩礦段Au元素的礦石量為441.632 9萬t,金屬量為10 992.982 1 kg,Au元素平均品位2.49×10-6。其中各礦體分類儲量匯總見表7,Au元素分布見圖11。可以看出,礦體空間形態變化和有用元素品位的空間分布。芒市主礦體產狀總體上較為穩定。但局部厚度變化大,主要是16線以北礦體厚度明顯變薄趨勢,在空間分布上也不均勻,元素品位之間相關性差,存在局部富集(16~20線)和貧化(向北或北北東)。
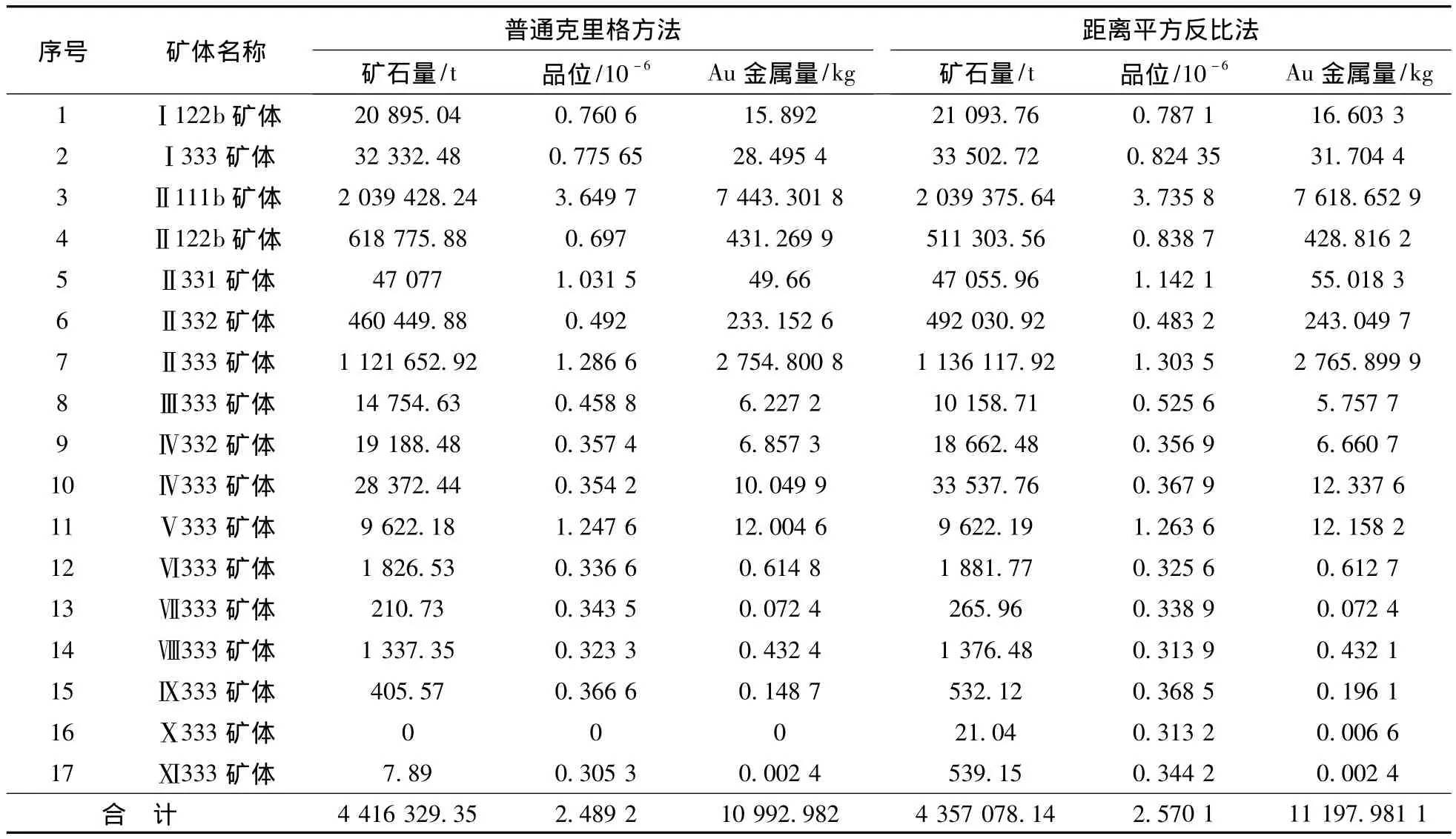
表7 普通克里格方法與距離平方反比法資源量估算結果Table 7 Estimation results of ore resource reserves by Ordinary Kriging and inverse distance method
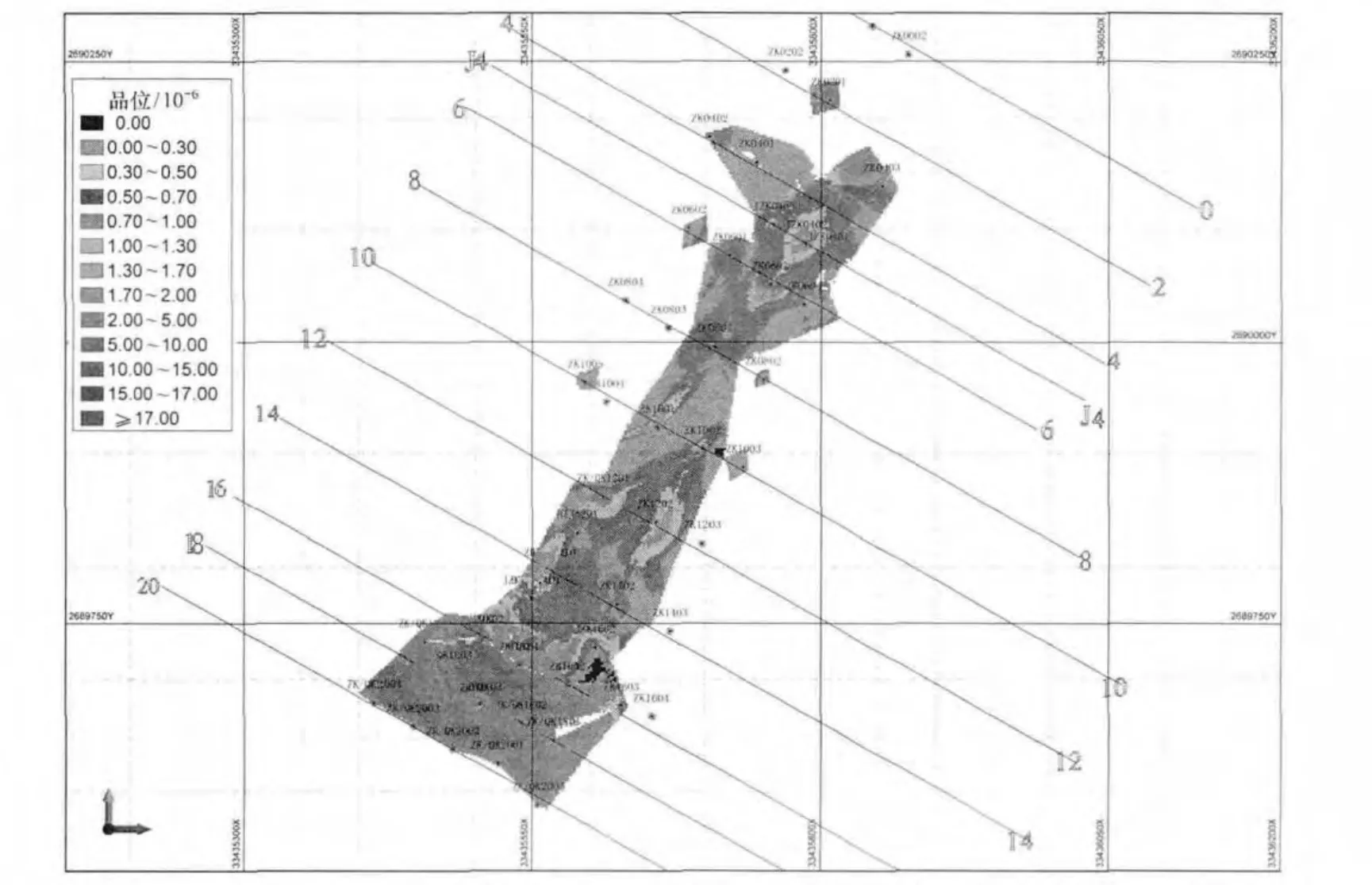
圖11 芒市麥窩壩礦段Au品位平面分布圖Fig.1 1Au grade plane distribution of Maiwoba ore section
為驗證資源儲量估算的可靠性,采用內部驗證和交叉驗證。交叉驗證采用與地質塊段法計算的資源儲量進行比較。驗證結果見表8。
由式(1)、(3)可知,普通克立格法估算資源量時,既考慮樣品空間位置,又考慮了樣品品位的變化,即樣品的分布不完全是均化的。它的科學性還體現在根據其變異函數可計算出在每一品位下的礦石量(圖12),便知在不同品位下需要挖掘的礦石量,以便今后礦山開采時計算成本。
5 結束語
(1)資源量的計算結果,Micromine的方法比傳統塊段法小,其原因是Micromine建模時嚴格按勘探線剖面圈定的礦體輪廓形態進行,剔除了夾石。
(2)利用Micromine計算數據的優勢,可統計出每一品位級別下的礦石量,即品位-噸位圖,可作為今后礦山開采計算成本的基礎數據。
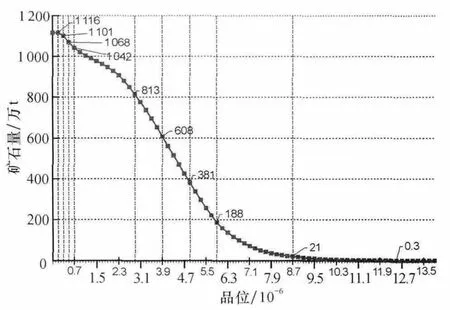
圖12 Au礦石量-品位曲線Fig.12 Au ore reserves-grade curve

表8 資源儲量可靠性交叉驗證Table 8 Cross-validation of ore resource reserves
[1]王義昭,李興林,段麗蘭,等.三江地區南段大地構造與成礦[M].北京:地質出版社,2000.
[2]饒文波,高振敏,楊竹森,等.云南潞西上芒崗紅色粘土型金礦地質特征[J].地質地球化學,2000,28(4):12-17.
[3]普傳杰,秦德先.云南騰沖-潞西金成礦帶地質特征與成礦預測[J].礦產與地質,2003,17(4):523-525.
[4]黎楓佶.西藏墨竹工卡縣甲瑪銅多金屬礦三維模型構建和資源量估算——基于MICROMINE的應用[D].成都:成都理工大學,2010.
[5]李賦屏,蔡勁宏,任建國.礦業軟件在礦產儲量評價中的應用[J].桂林工學院學報,2005,25(1):26-30.
[6]陳東越,陳建平,陳三明,等.遼東白云金礦地質體三維模型的構建與儲量估算[J].桂林理工大學學報,2013,33(1):14-20.
[7]王麗梅,陳建平,唐菊興.基于數字礦床模型的西藏玉龍斑巖型銅礦三維定位定量預測[J].地質通報,2010,29(4):565-570.
[8]鄭文寶,黎楓佶,唐菊興,等.基于Micromine軟件下地質統計學在甲瑪矽卡巖型銅多金屬礦儲量計算中的應用[J].地質與勘探,2011,47(4):726-736.
[9]侯景儒,尹鎮南,李維明,等.實用地質統計學[M].北京:地質出版社,1998.
[10]高航校,任小華,李福讓,等.克里格方差在礦產資源量分類中的應用研究[J].硅谷,2011(15):121,85.

