基于矢量傳感器的空中脫靶量測量方法研究

綦笑微，高洪舉，馬麗麗，董佳新，宋文利

(中國白城兵器試驗中心，吉林 白城137001)

0 引 言

在連續介質聲場中，任意一點附近的運動狀態可用聲壓p，密度ρ 及介質質點振速v 唯一表示［1］。聲壓是標量，振速是矢量，其方向與波到達的方向一致。傳統的聲學定位系統采用聲壓傳感器陣列，利用信號傳播時間延遲確定目標的方位，屬于標量測量，沒有利用聲波的矢量信息。近年來，利用聲波矢量場的聲矢量傳感器技術已經在水聲領域開始廣泛的重視和探索研究，其具有單陣元定向，方位分辨率高、抑制柵瓣等優點［2］。

現有聲學脫靶量測量系統均屬于標量測量［3］。如果將矢量傳感器技術引入到現有聲探測的研究中，可以實現聲脫靶量測量的三維矢量定位。要進行矢量測量就需要振速信息，國內現有矢量傳感器，主要針對水聲測試原理，不適用空氣范圍內，這樣就給直接獲取振速帶來一定困難。對此本文開展研究，分析聲壓、振速關系特性，利用現有聲壓傳感器構造了基于壓差原理的三維聲矢量傳感器，提出聲壓、質點振速聯合信息處理的空氣聲矢量定位思路，采用復聲強法利用聲壓、振速互譜實現了目標的到達方向(direction of arrival，DOA)估計，并通過概率法實現了多基陣的目標聲學定位。

1 矢量聲學傳感器的布陣方案設計

1.1 目標聲場聲壓與振速之間的關系

設聲場中某點r 處的聲壓為p(r，t)，振速為v(r，t)，聲源的目標方向為(β，θ)。系統坐標系如圖1 所示。對于均勻平面波聲場，聲學的運動方程［4］

在上式中可以由r 方向上距離為Δr 的相近兩點(kΔr?1，k 為波數)的聲壓值p1(r，t)，p2(r，t)近似求得振速［5］

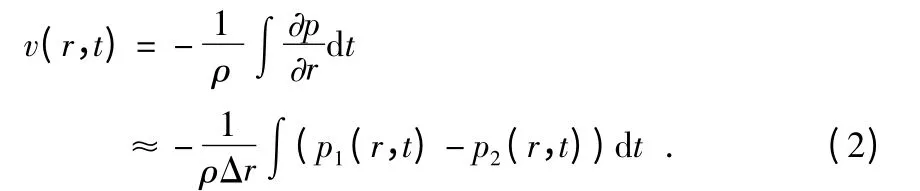
1.2 三維聲學矢量傳感器構建

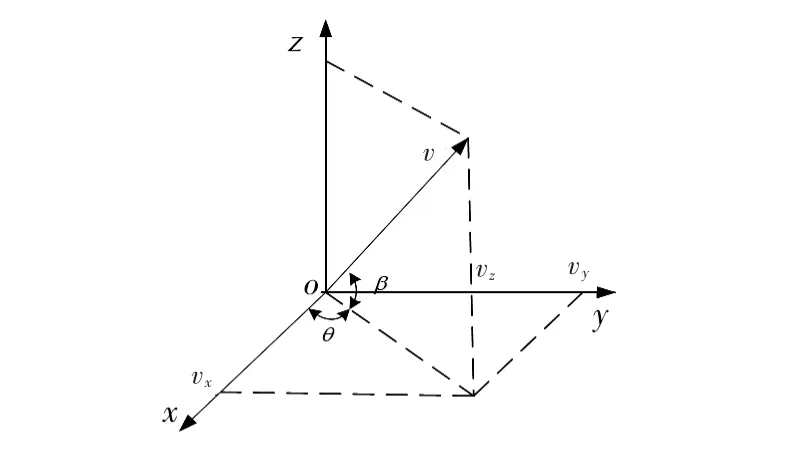
圖1 振速及其3 個正交分量的投影圖Fig 1 Projection of vibration speed and three orthogonal components

根據式(2)給出的同點聲壓、振速的關系特性，可以在3 個坐標軸上分別布設2 個近距離聲壓傳感器構建一個基于壓差原理的三維矢量傳感器，以獲取矢量振速信息。三維矢量傳感器與被測目標的聲源入射方向存在如圖2 的位置關系。設目標滿足遠場條件，矢量傳感器在x 軸方向上的陣元記為1，2，接收到的聲壓分別記為p1(t)，p2(t);y軸方向上的陣元記為3，4，接收到的聲壓分別記為p3(t)，p4(t);z 軸方向上的陣元記為5，6，接收到的聲壓分別記為p5(t)，p6(t)。

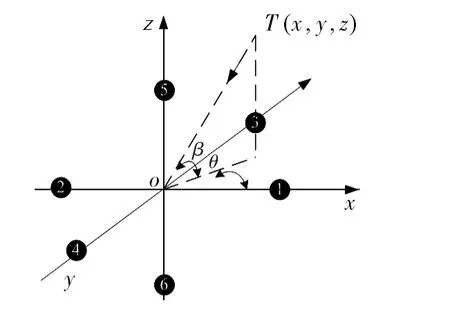
圖2 目標入射方向與矢量傳感器位置關系Fig 2 Position relationship between incident direction of target and vector sensor

1.3 空中脫靶量測量布陣設計

現有聲脫靶量測量系統采用直線一字型空中吊靶布陣方式，屬于二維測量，不能進行三維定位。這樣就限制了其試驗使用范圍。如果采用傳統聲壓傳感器進行空間大尺寸布陣，利用幾何關系進行結算來確定三維脫靶量坐標，既存在具體布站困難，又存在由于空中扭曲、型變所引起的誤差。如果將本文設計構建的矢量傳感器進行封裝、固化，選取一定數量組成線型陣布設于靶機下面可以實現脫靶量的三維矢量測量，其結果如圖3 所示。

2 基于聲壓與質點振速聯合的聲矢量波達方向估計

2.1 三維矢量傳感器目標定向原理

設矢量傳感器各陣元距陣中心o 的距離均為D，信號頻率為fo，根據矢量傳感器輸出的振速的三個分量可得到目標的俯仰角β 和方位角θ

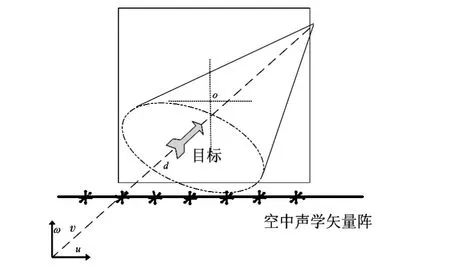
圖3 矢量傳感器空中脫靶量測量布陣示意圖Fig 3 Airy miss distance measurement embattle diagram of vector sensor

由于同一點的聲壓和質點振速是完全相關的，而其測量噪聲是不相關的。因此，可以聯合處理每個聲矢量傳感器測得的聲壓和質點振速信息，有利于減小噪聲的影響，提高聲矢量傳感器的定向能力。

由于［6］

其中，I 為聲強，即取能流密度的時間平均值表示聲波能量的強度;T 為平均時間;p 為聲壓。

可知，聲場中同一點處的聲強方向與該點處的質點振速方向相同，即每個聲矢量傳感器處的聲強方向也為目標相對于該聲矢量傳感器的方向。用聲場中某點r 處的聲強在3 個軸上的分量確定俯仰角和方位角為

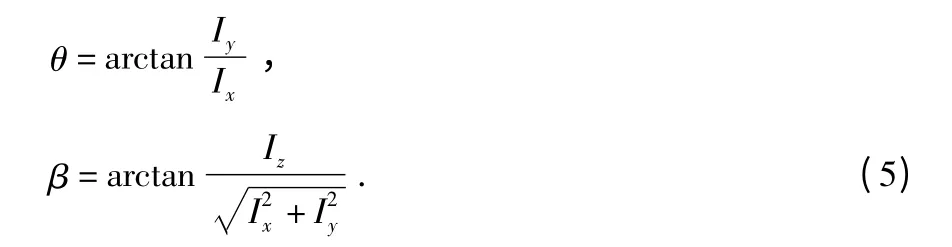
在無干擾的理想情況下，式(3)和式(5)給出相同的結果;在有干擾時，式(5)結果將優于式(3)。

2.2 基于矢量傳感器的目標DOA 估計

由于目標信號的聲壓和振速是相關的，而各種同性環境干擾中聲壓和振速是不相關的或相互很弱［7］，因此，利用聲強來確定波達方向具有良好的抗干擾性。基于平均聲強只能用于單目標的方位估計，復聲強測向可以分辨頻譜有差異的多目標方位，所以，采用聲壓、振速互譜來測向。

在時域中，聲強等于相同時刻聲壓與振速的相關函數，即

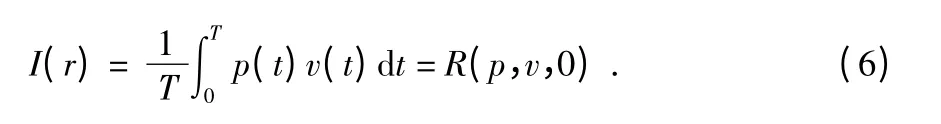
在頻域中，與互相關函數相對應的量為互譜密度函數，即

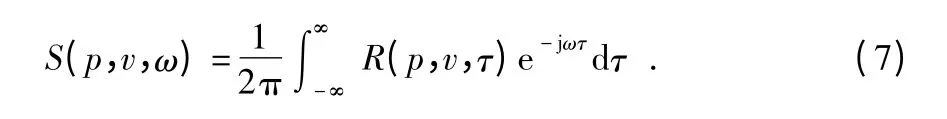
式(7)將時域中的互相關函數轉換為頻域中互譜密度函數。相反地進行傅里葉逆變換就可經頻域互譜密度函數轉換為時域對應的互相關函數，即為

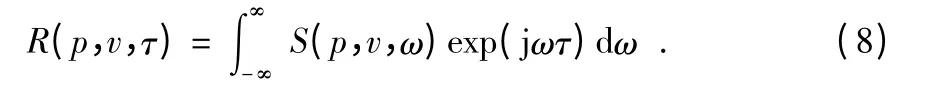
對p(t)和vi(t)(i=x，y，z)作Fourier 變換，得到相應的譜為p(ω)和Vi(ω)，則聲壓、振速互譜(互功率譜密度函數)為

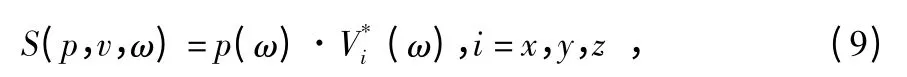
式中 *表示共軛運算。

將式(8)代入式(6)，有

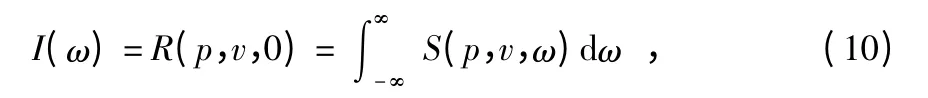
并根據傅里葉變換基本特性，2 個同相位輸入的能量集中在互譜的實部，即可得到原點o 處聲強在3 個軸上的分量

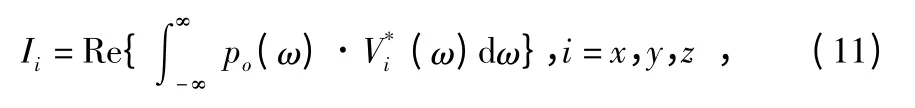
式中 po(ω)為原點o 處的聲壓的Fourier 變換，Vi(ω)為原點o 處的3 個振速分量的Fourier 變換。

下面分別計算po(ω)和Vi(ω):

由于兩點連線中點的聲壓可近似表示為兩參考點的平均值，所以，po(ω)可以表示為

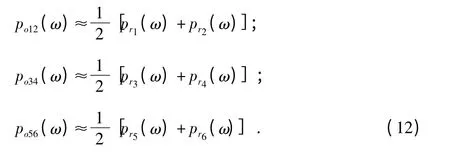
對式(2)取Fourier 變換，得

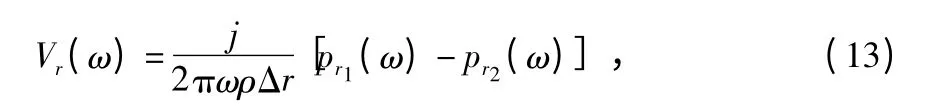
即得到原點o 處的三個振速分量的Fourier 變換。

綜合以上分析并代入式(5)可得到目標聲源的DOA 估計

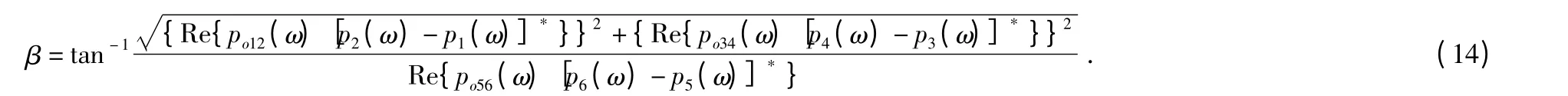
3 基于概率的多基陣被動聲定位原理

用概率的觀點來看，目標位置落在空間不同點的概率密度是不一樣的。目標位置落在測量子集上的概率要大一些，落在測量子集以外的區域，距測量子集越遠概率越小。多個基陣將形成多個測量子集，目標落在空間某一點的概率就應由多個測量子集對應的多個概率而定。根據分析，在整個空間內總的概率密度函數只有一個峰值，故可以將該峰值對應的位置作為多基陣的定位結果。系統布陣如圖4所示，聲源坐標為(x，y，z)。

由多種測量誤差所形成的實際誤差分布呈正態分布，即某個意義的測量ω 的具體測量結果為ω'，可以用ω 的概率密度函數來描述，即

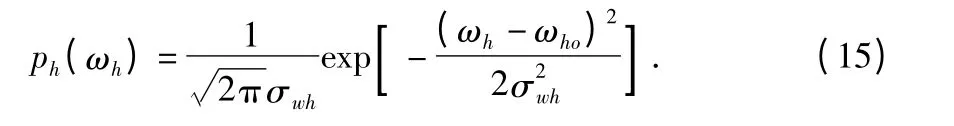
設具體的測量w 對應一個子集，它所給出的坐標點與測量值之間的關系為

下面需通過每個的測量基陣的結果來確定關系式(16)。系統的n 個基陣，其坐標為(xh，yh，zh)，h∈{1，2，3，…，n}，每個單基陣，其測得的目標俯仰角為βh、方位角為θh。這樣，對于單基陣h 可以用俯仰角為βh、方位角θh實際估計值為(βho，θho)。假設目標的方位角和俯仰角不相關，其概率密度函數可表示為

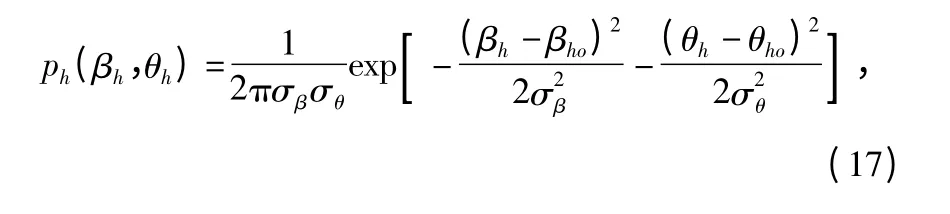
將復雜的非線性問題線性化。將(18)式在(x0，y0，z0)((x0，y0，z0)可取幾何交叉法的定位結果)附近的區域，采用泰勒級數展開的辦法，取一級近似并帶回式(17)，經計算得到單基陣定位的概率密度函數可寫成

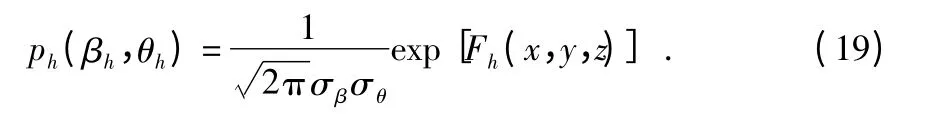
假設基陣與基陣之間相互獨立，對于多個基陣聯合估計目標位置的情況，其概率密度函數應為單個基陣概率密度函數的乘積。多基陣系統的概率密度函數可寫為

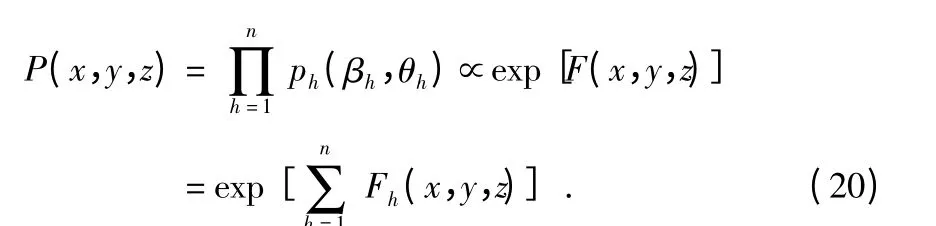
求解目標位置的過程為求解概率密度函數最大點的過程。對分別求總概率密度函數的指數F(x，y，z)對X，Y，Z的導數，并令其等于零，由此可得求解目標位置的方程組為

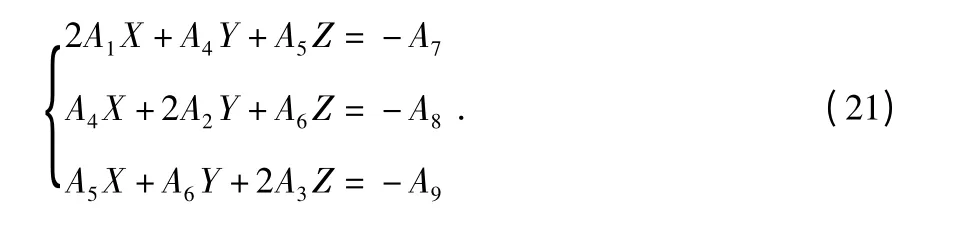
從上式可以看出，當線性方程組的行列式不為0 時，目標位置有唯一解。

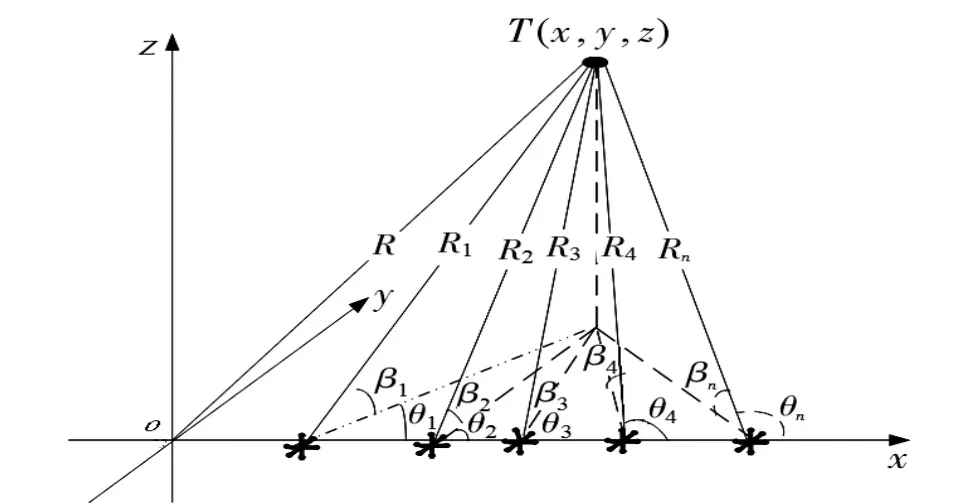
圖4 多基陣系統布陣示意圖Fig 4 Diagram of multi－array system embattle

4 仿真實驗與精度分析

采用實測的炮口聲音數據，對基于三維壓差式矢量傳感器復聲強測量的目標定位在各種條件下的估計精度進行仿真實驗研究。本節仿真實驗采用的炮口聲信號的采樣頻率為100 kHz，火炮距離矢量傳感器幾何中心的距離為1 000 m，空氣聲速取c=340 m/s。

4.1 不同矢量傳感器尺寸時的目標DOA 估計精度

取SNR=30 dB，積分時間取為T=1 s，目標的俯仰角為60°，方位角在-180°～180°之間變化時，不同矢量傳感器尺寸R 時的目標方位角估計精度如圖5 所示。目標的方位角為45°，俯仰角在0°～90°之間變化時，不同傳感器尺寸R時的目標俯仰角估計精度如圖6 所示。

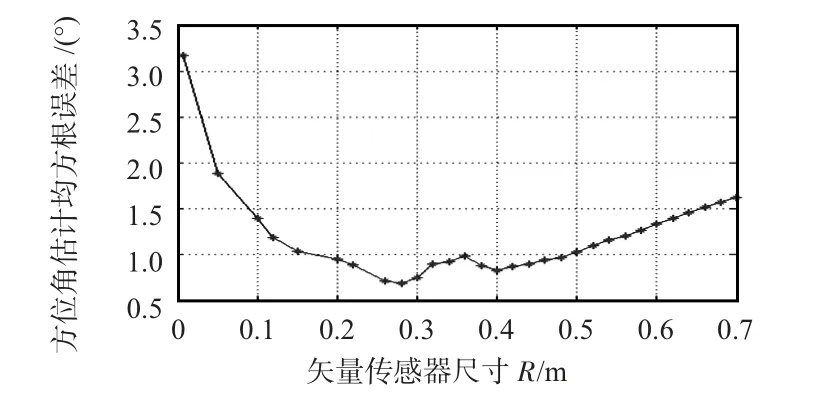
圖5 不同傳感器尺寸時的目標方位角估計精度Fig 5 Target azimuth angle estimation precision with varying size of sensor

圖6 不同傳感器尺寸時的目標俯仰角估計精度Fig 6 Target pitching angle estimation precision with varying size of sensor

通過仿真可以看出:在一定的信噪比和積分時間下，目標DOA 估計的精度隨矢量傳感器尺寸的增大先增大，后減小。陣的尺寸為D=0.15 m 時，目標的俯仰角估計精度最高。綜合考慮，選取式矢量傳感器的尺寸R=0.25 m 時，可以獲得最佳的DOA 估計精度。

4.2 不同積分時間時的目標DOA 估計精度

取SNR=30 dB，矢量傳感器尺寸取R=0.25 m。目標的俯仰角為60°，方位角在-180°～180°之間變化時，不同積分時間時的目標方位角估計精度如圖7 所示。目標的方位角為45°，俯仰角在0°～90°之間變化時，不同積分時間T 時的目標俯仰角估計精度如圖8 所示。

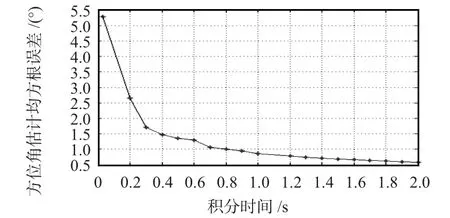
圖7 不同積分時間時的方位角估計精度Fig 7 Precision of target azimuth angle estimation at different integral times

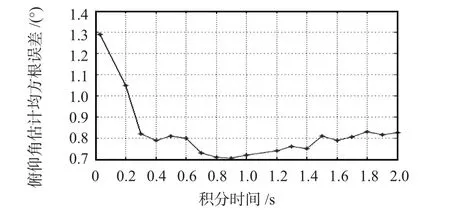
圖8 不同積分時間時的俯仰角估計精度Fig 8 Precision of target pitching angle estimation at different integral times

由實驗結果可知，目標方位角的估計精度隨積分時間的增大而提高，當積分時間大于0.8 s 時，目標方位角估計的均方根誤差小于1°;當積分時間小于1 s 時，目標俯仰角估計精度隨積分時間的增大而提高，但當積分時間大于1 s時，俯仰角估計精度有所降低;積分時間大于0.25s 時，目標俯仰角估計精度在1°以內;積分時間為1s 左右，俯仰角估計精度為0.8°。

4.3 矢量傳感器空中脫靶量定位精度分析

傳統聲脫靶量測量系統采用聲壓傳感器構成，測量中沒有利用聲波的矢量信息，只能進行垂直于入射方向的傳感器直線陣列所在平面的二維坐標定位，并且其垂直方向結果是應用水平方向傳感器時間差擬和得到的，往往誤差很大(最大可能達到十幾厘米)。假定聲脫靶量測量系統的脫靶量測試靶幅為8 m×8 m。矢量傳感器的定向精度為0.8°。就三維定位精度進行簡單推算，其可以實現定位誤差7 cm 以內的三維坐標定位，這樣就大大擴展了其設備的使用范圍。

5 結 論

1)基于聲壓、質點振速聯合信息處理的聲矢量定位方法，可以實現空氣中目標的聲學定位。矢量傳感器可以用于空中脫靶量測量，可是實現10 cm 以內誤差的三維坐標測試。

2)用聲壓、振速互譜實現目標的方向估計，可以抵消各項同性的噪聲干擾，信號不變，從而提高信噪比。

3)由于復聲強定向的多目標分辨優勢，可以利用矢量傳感器來進行多目標的定位、運動目標的軌跡跟蹤，并可以開展相關領域的矢量聲定位技術研究。

［1］ 趙 微.矢量傳感器陣高分辨方位估計及其穩定性研究［D］.哈爾濱:哈爾濱工程大學，2008:2-3.

［2］ 陳麗潔，張 鵬.矢量水聽器綜述［J］.傳感器與微系統，2006，25(6):5-8.

［3］ 綦笑微，張 軍.聲脫靶量測量系統誤差分析［J］.兵器試驗，2006(3):67-68.

［4］ 惠俊英，惠 娟.矢量聲信號處理基礎［M］.北京:國防工業出版社，2009.

［5］ Thompson J K，Tree D R.Finite difference approximation errors in acoustic intensity measurements［J］.J Sound and Vibration，1981，75(2):229-238.

［6］ 蔡宗義，趙俊渭.低頻小尺寸高精度空中運動目標定位算法［J］.火力與指揮控制，2008，33(11):148-149.

［7］ 白興宇.基于聯合信息處理的聲矢量陣測向技術［D］.哈爾濱:哈爾濱工程大學，2006:11-15.