魚雷錨的方向穩定性研究
董天宏,黃海科,柯鵬飛
(1.華南理工大學土木與交通學院,廣州 510640;2.廣州航通船業有限公司,江門 529145)
1 引 言
目前,烴類礦物的開采已進入3 000 m的超深水領域。為了穩定系泊用于開采的海洋平臺等水上結構物,需要開發更優越的錨固系統。魚雷錨與常規錨相比顯現出更有發展前景的深水系泊,解決方案的部件較少,更容易施工,更簡單的安裝,并能大幅度降低成本等優勢。重力錨的概念首先由Atturio和Valent在1977年提出[1],作為海洋熱能守恒(OTEC)電廠的成本有效且可行的系泊選項。巴西國家石油公司Petrobras對魚雷形重力錨的研究項目于1996年被首先提出,魚雷錨最早在2002年被投入商業應用于巴西的坎普斯盆地。最近針對魚雷錨的研究有所加深。大多數的研究都是為了更好地貫穿海床,從而找到在自由落體中增強尤其是方向穩定性這方面的水動力特性的方法。
本文提出了一種使用CFD模型魚雷錨下降的安裝過程,并分析水動力參數對重力錨的方向穩定性的影響的方法及其所得的結果。
2 方向穩定性的數值分析
魚雷錨的方向穩定性受許多參數如重量、重心、水動力中心等各結構形式的影響。它也可以由魚雷錨落下后的位移距離和旋轉角度進行評估。
2.1 重量和重心的影響
該研究對沒有連接纜繩錨鏈等連接裝置的未經改裝的母型魚雷錨進行了研究。該母型魚雷錨模型直徑和長度分別為1.2 m和13 m,如圖1所示。由于魚雷錨軸部添加加碴混凝土和廢金屬,配重會對方向穩定性產生一些影響。
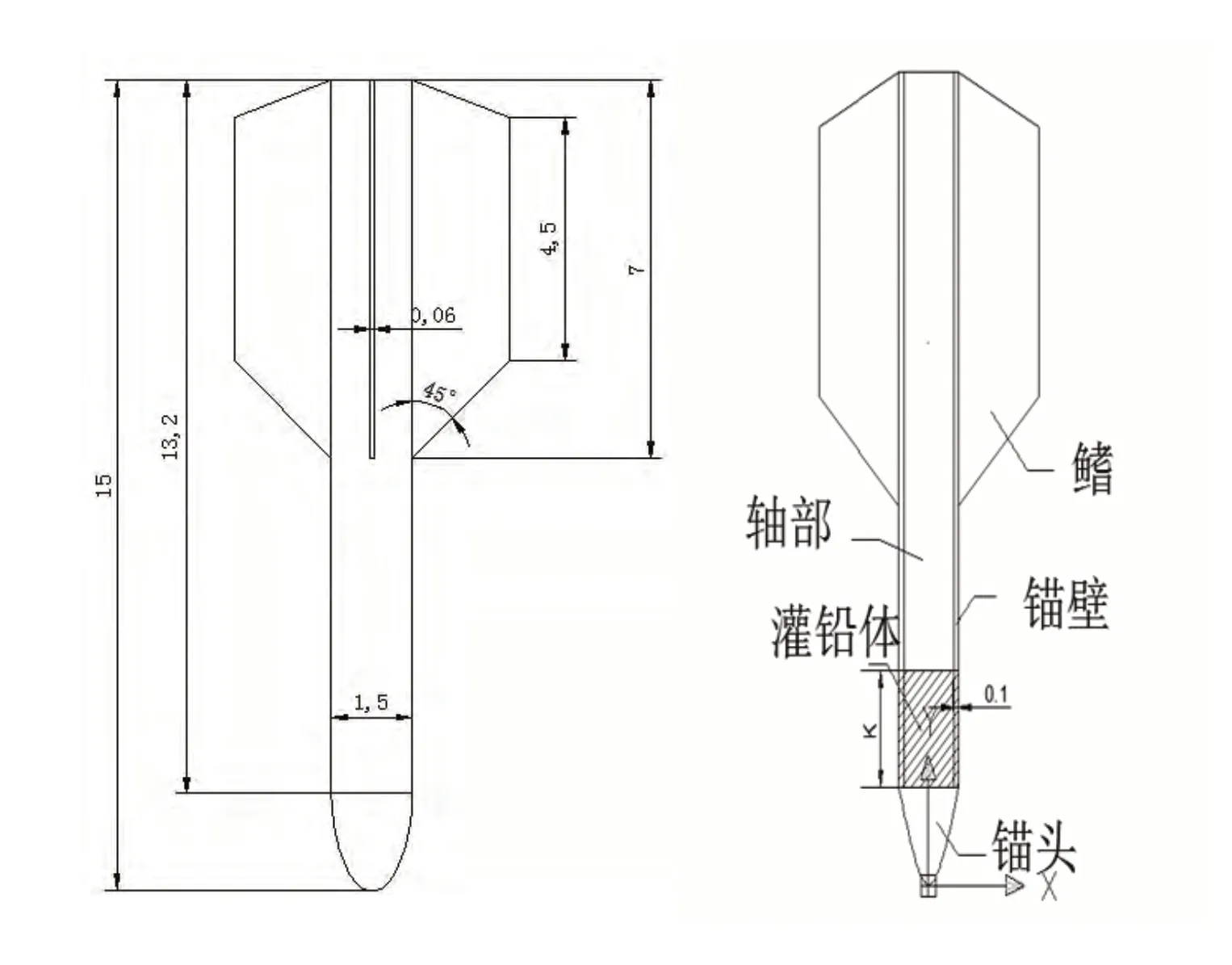
圖1 魚雷錨外形尺寸與配重尺寸圖
魚雷軸部的配重部分和其他結構部件的分別由鉛(密度11 300 kg/m3)和鋼制成(密度為7 850 kg/m3),如圖1所示。每個部分的重心為可以通過加入配重部分的高度k進行計算,然后,整個魚雷的重心高度CG(XG)通過推導可以表示為:
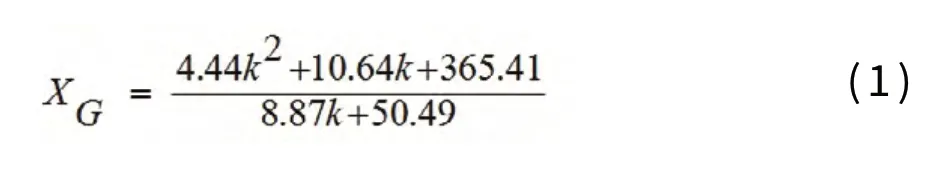
顯然,要如果能得到較小的XG,即可使魚雷的方向更加穩定。 XG得到最合適的值為2.8 m。該模型命名為H2.8,通過使用CFD軟件進行模擬該模型從2 700至3 100 m的海底模型的400m的高度的落下過程(用“H”和“k值”命名)。
而加大軸部配重重量的意義在于當小幅改變中心高度的情況下提高魚雷錨體的密度,令魚雷錨型保持不變,同時重量增大為原來的2倍,即將密度假設為原錨的2倍進行模擬得到結果如圖2、3。
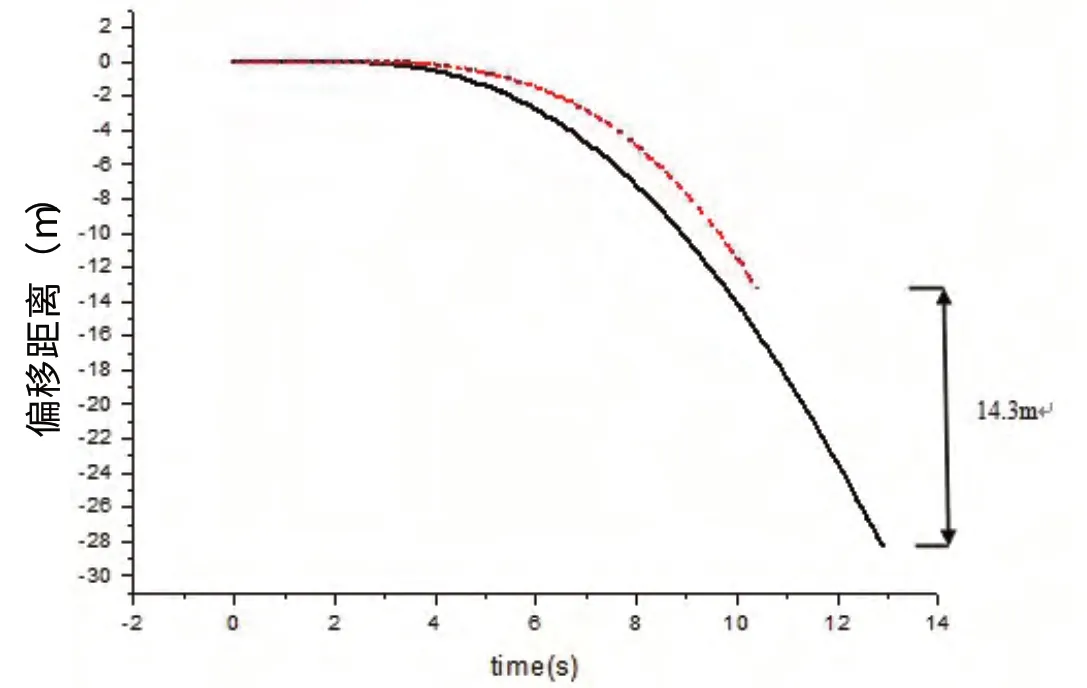
圖2 400 m下落后2倍重型與母型魚雷錨偏移距離對比

圖3 400 m下落后2倍重型與母型魚雷錨偏轉角度對比
圖2、3分別顯示在400 m下落安裝過程中的偏移距離和偏轉角度與母型錨數據的對比情況,其中虛線所代表的為2倍重魚雷錨的下落情況數據,實線代表母型錨的下落情況數據。
針對兩種錨型的方向穩定性對比如表1所示
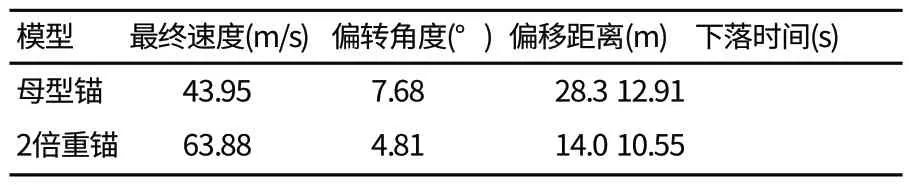
表1 2倍重魚雷錨與母型錨下落400 m時的方向穩定性對比
可以看到在密度增大一倍的前提下,魚雷錨方向穩定性大幅度提升且下落時間大大減少,但如果為了達到此目的必需要將魚雷錨空心的軸部填滿(因為只有這樣才能大幅提升密度,在自然界中并不存在成本與密度都能接近2倍原密度的假設情況的材料),很顯然這樣會使魚雷錨重心的位置又會過于偏高,那么絕對無法得到足夠的方向穩定性,故我們取k=2.8 m,此后研究中的母型錨均以軸部加入2.8 m的錨型為準。
2.2 尾翼的影響
為了評價尾翼對魚雷錨方向穩定性的影響,創建從H2.8的原型與0.064長寬比的模型,命名為SAR(小長寬比)。由于通過模擬發現在較小的下落距離里更小的展弦比的錨型率先加速度達到接近于零的數值,繼續下落只會增大偏移量與偏轉角度并可能損失當前達到的速度,故只取下落的前10.5 s的方向穩定性數據圖進行對比。
兩個模型(母型錨與SAR型)的仿真結果如圖4、圖5,結果數據對比見表2,可看出由于SAR具有較小展弦比使其在較小的下落時間段內的方向穩定性相對母型錨較好。
由數據對比可知,在較小的展弦比下原魚雷錨在與母型錨下落同樣的較小的距離時,其轉角相對增大,偏移距離相對減小,終速稍減,這說明在相對較小的下落距離中總的魚雷錨的水動力系數是弱于原母型錨的。在方向穩定性方面也同樣如此,雖然便宜的距離相對的減少但終態時的偏轉角度卻增大了近50%。而且這一切的數據還是在兩種錨型達到終速之前的對比結果,可以預見在同樣下落400 m的距離的情況下由于小展弦比錨率先達到終速,則繼續下去會進一步損失其本就相對較小的動能,而且在海洋環境的影響下不再繼續加速的新型錨將會大大損失其方向穩定性,由此可見,過小的展弦比在魚雷錨的結構中是不可取的。
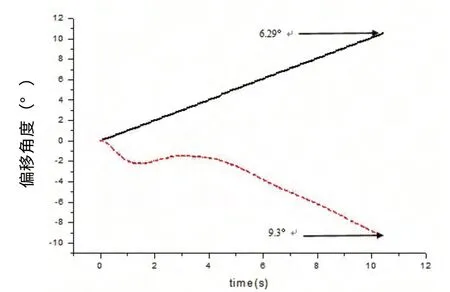
圖4 下落10.5 s內小展弦比型與母型魚雷錨平移距離對比
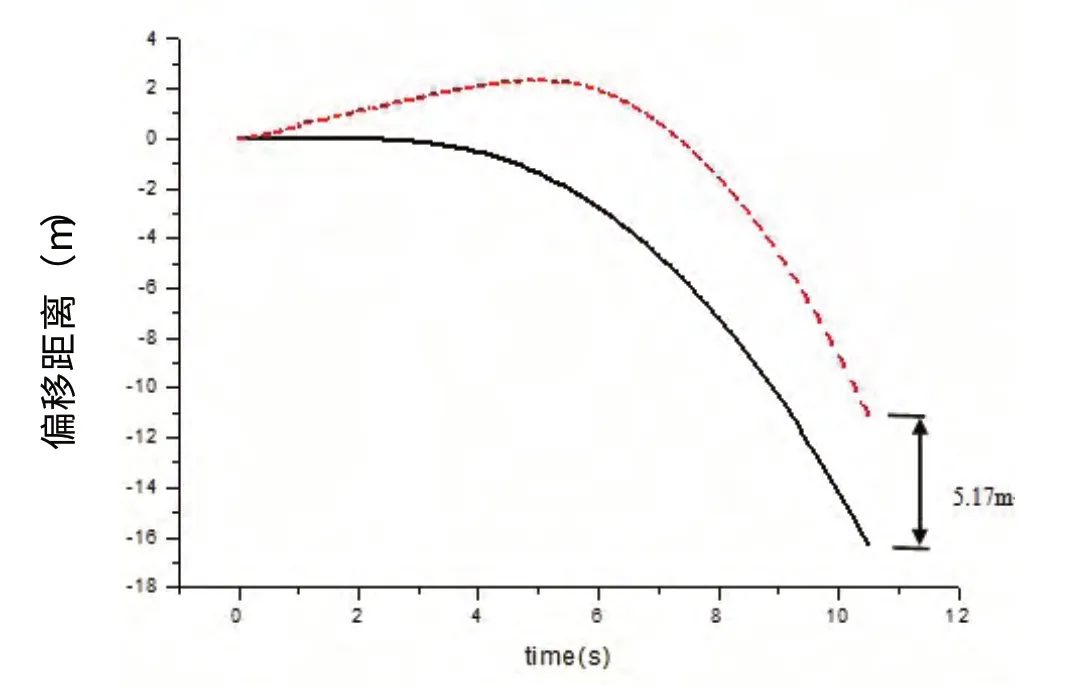
圖5 下落10.5 s內小展弦比型與母型魚雷錨平移距離對比
圖4 、圖5分別顯示在下落安裝過程的前10.5 s中的偏移距離和偏轉角度與母型錨數據的對比情況,其中虛線所代表的為小展弦比魚雷錨的下落情況數據,實線代表母型錨的下落情況數據。

表2 結果對比
2.3 細長體型長寬比對方向穩定性影響的討論
為保持除錨體主干部分以外的其他部分參數不變,加大錨體的長度至23.4 m,并同時減小寬度至1.2 m,則重心高度按比例變到14.23 m處,轉動慣量按長度平方比例變化為2 100 762.7 kg·m2。經過模擬發現細長體型魚雷錨在11.9 s的時間點就已經完成下落400 m的安裝任務,故細長體型魚雷錨的水動力數據只取11.9 s。
其模擬方向穩定性結果及模擬結果數據分別呈現于圖6、7與表3之中。
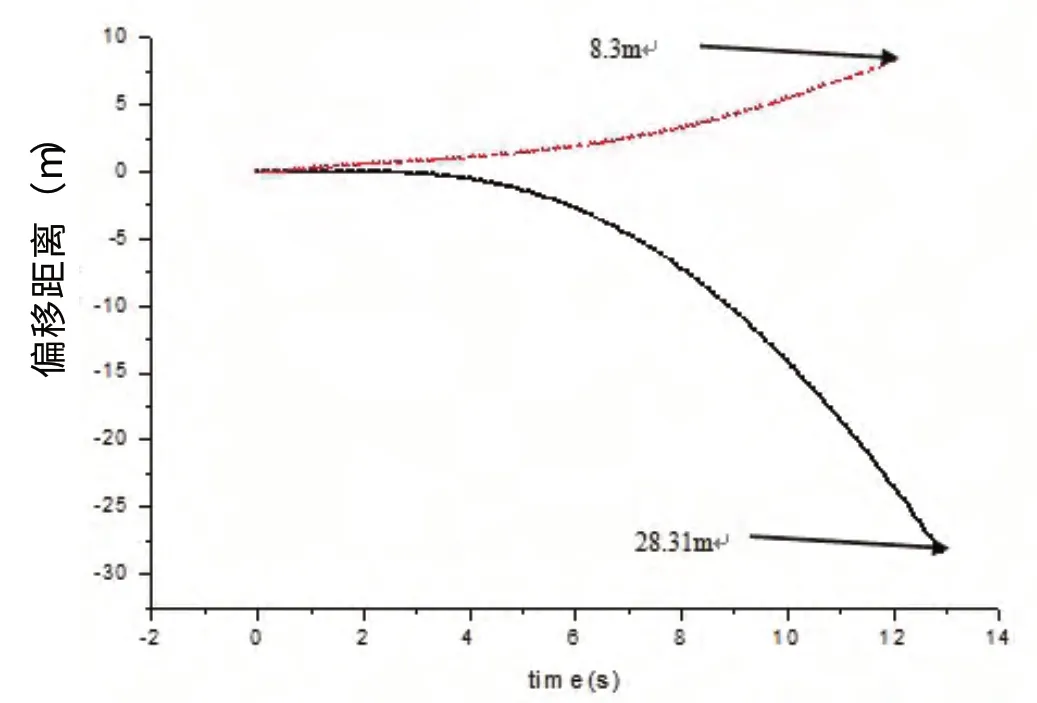
圖6 下落400 m 細長體型與母型魚雷錨平移距離對比
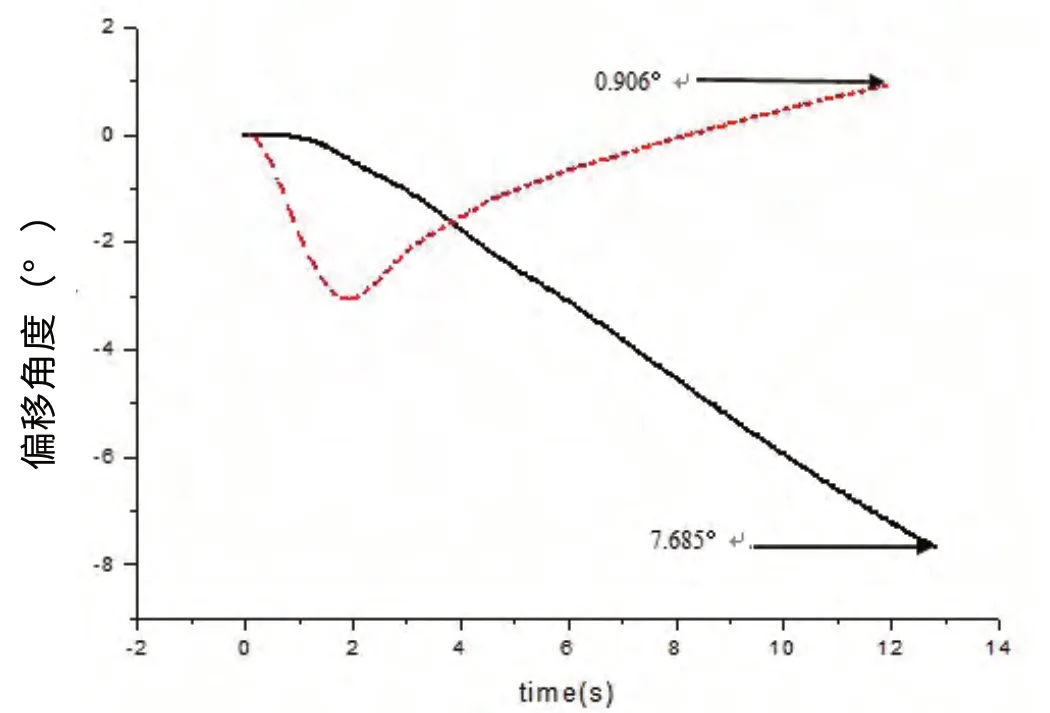
圖7 下落400 m 細長體型與母型魚雷錨偏轉角度對比
圖6 、7分別顯示細長體型魚雷錨在400 m下落安裝過程中的偏移距離和偏轉角度與母型錨數據的對比情況,其中虛線所代表的為細長體型魚雷錨的下落情況數據,實線代表母型錨的下落情況數據。

表3 細長體與母型錨下落方向穩定性參數對比
由以上結果對比可知改變成為細長體后,不但加快了終速減短了下落時長,同時又大大增強了方向穩定性。但實際應用中考慮到魚雷錨的抗折強度,一般不會取太大的長寬比,以防止出現不必要的損失。
2.4 對水動力中心和方向穩定性恢復能力之間的關系進行討論
當重力的魚雷錨的中心(CG)低于其流體動力學中心(CH)下,它被看作是定向的穩定,否則它是不穩定的。一般地,CG應比CH小錨長度[3]的10%左右。對于魚雷錨沒有尾鰭的情況,CH是從錨頭開始計算,計算公式如下:
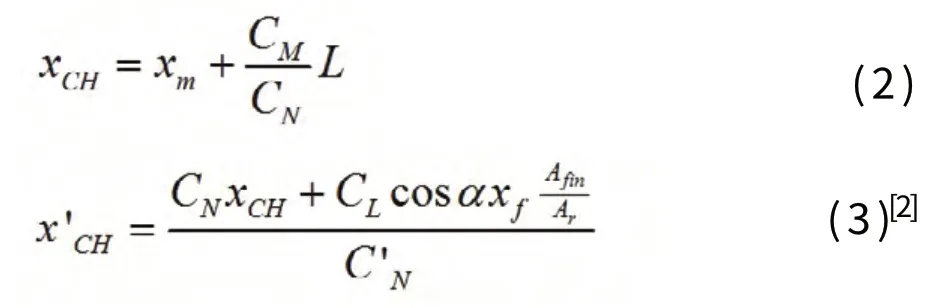
其中,CL是基于鰭平面形狀面積(Afin)的升力系數。
對小展弦比 的鰭可以使用瓊斯公式:

Afin為鰭平面面積,xf為魚雷錨前段端點至鰭平面中心的距離。式中的新系數C’N定義為:
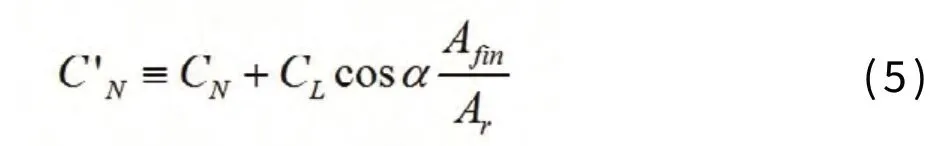
其中,Afin是尾翼所在區域的橫截面積,Ar是主體部分橫截面積,α是攻角。
3 結 論
我們對魚雷錨的方向穩定性進行了系統研究。模擬結果表明,重心和水動力中心的相對位置必須在評估錨的穩定性時加以考慮。且在不改變魚雷錨總體形狀的同時加大自身重力,可大大提升以方向穩定性為主的各種水動力性能。在實際應用中,一般采取在魚雷錨體中空軸部填充大密度配重,雖無法達到2倍原錨體平均密度的效果,但仍舊是很有效的方法之一。通過研究還可知,尾翼和細長體型魚雷錨可顯著提高方向穩定性,雖然隨前者的減小而這些優勢只適用于一定的下落范圍內,且相對于其對方向穩定性的作用并不明顯,下落速度的輕微犧牲是不可以接受的。而后者則可以說在符合穿透海床的允許范圍內并綜合考慮魚雷錨的壽命與造價的情況下可取的值越大越好,因為其可以對水動力系數尤其是方向穩定性的好處是巨大的。
[1]J.M.Atturio and P.J.Valent, “High-capacity, deep-water, free-fall anchor,”C.Proceedings of OCEANS’77 Conference (1977).
[2]Antonio Carlos Fernandes, “Torpedo Anchor Installation Hydrodynamics,” J.Journal of Offshore Mechanics and Arctic Engineering, Vol.128, No.4 (2006).
[3]Mohammad S.Raie, and John L.Tassoulas, “Installation of Torpedo Anchors:Numerical Modeling,” J.Journal of Geotechnical and Geoenvironmental Engineering (2009).

