不同加載速率下梁柱邊節點的抗震性能

范國璽，王德斌，楊樹桐，郭海燕，宋玉普

(1.中國海洋大學工程學院，山東青島266100;2.大連交通大學土木與安全工程學院，遼寧大連116028;3.大連理工大學海岸和近海工程國家重點實驗室，遼寧大連116024)

鋼筋混凝土梁柱節點，是影響整體結構抗震性能的重要構件，且梁柱節點變形對框架變形影響較大。國內外現行規范關于梁柱節點的抗震設計方法，主要以擬靜力試驗結果為基礎。事實上，這種擬靜力試驗的應變率水平往往低于地震作用下的應變率水平(10－4～10－1)［1］。

自Abrams［2］對混凝土進行動載(應變速率約為2×10－4/s)和靜載(應變速率約為8×10－6/s)壓縮試驗時發現混凝土抗壓強度存在速率敏感性以來，不少研究人員發現，混凝土和鋼筋具有速率敏感性。Bischoff［1］、Malvar等［3］分別總結了荷載速率對混凝土抗壓、抗拉特性的影響，指出10(°)/s左右是一個臨界值。我國《水工建筑物抗震設計規范》(DL5073-2000)［4］規定:除水工鋼筋混凝土結構外的混凝土，水工建筑物的抗震強度計算中，混凝土動態強度和動態彈性模量的標準值可較其靜態標準值提高30%。Manjoine［5］指出，低碳鋼的屈服應力隨應變率的提高而提高。Knobloch等［6］發現，溫度升高的情況下，應變率對低碳鋼應力－應變關系有顯著影響。

受材料速率敏感性的影響，鋼筋混凝土構件具有速率敏感性，其強度、剛度在不同應變率水平下均有所不同。Mutsuyoshi等［7］發現，鋼筋混凝土梁在較高應變率水平下，傾向于脆性剪切破壞。Adhikary等［8］指出，鋼筋混凝土梁的極限承載力隨應變率的提高而提高。Lamarche等［9］發現，高應變率提高了柱的屈曲與后屈曲強度。Bhowmick等［10］指出，較高應變率水平下，鋼板剪力墻的延性降低。然而，對于動態荷載作用下，鋼筋混凝土梁柱節點性能的研究相對較少。基于上述考慮，研究了地震荷載作用范圍內，加載速率和軸壓比對鋼筋混凝土梁柱邊節點動態性能的影響。

1 試驗概況

1.1 試件制作

試驗針對中間層邊節點進行研究，為方便試驗，不考慮橫梁的約束作用，從而將空間節點簡化為平面構件，試驗證明，這種簡化處理是偏于保守的［11］。分別在水平方向和豎直方向上，梁柱反彎點處將其截斷，得到梁柱節點組合體單元。框架梁與框架柱相交的部分為節點核心區，節點核心區以及節點核心區鄰近的框架梁端、柱端，稱為節點組合體。

試件柱和梁的抗彎承載力按照Mc＞1.4Mb設計。混凝土強度等級選用C30，縱筋選用HRB335級鋼筋，箍筋選用HPB235級鋼筋。梁柱截面形式均選擇矩形截面，其截面尺寸b×h分別為250 mm× 400 mm、350 mm×350 mm。試件長1.6 m、高3 m。試驗共制作3個試件，截面尺寸和配筋率相同，試件截面尺寸、配筋詳圖如圖1所示。試驗前測得材料參數見表1、2。

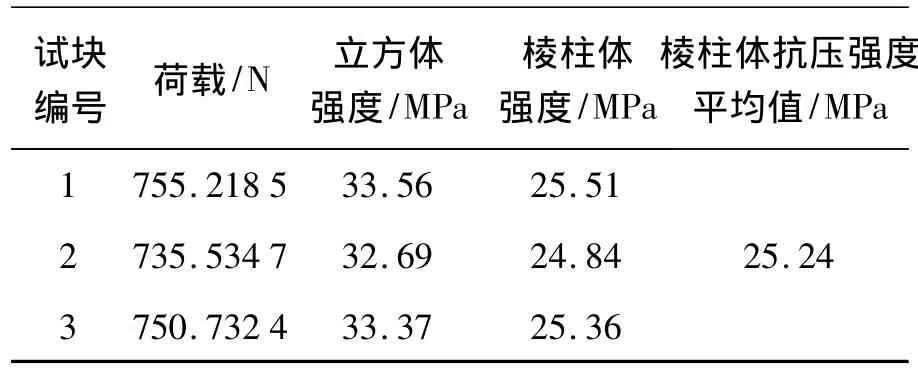
表1 混凝土材料試驗數據Table1 Compression strength of the concrete

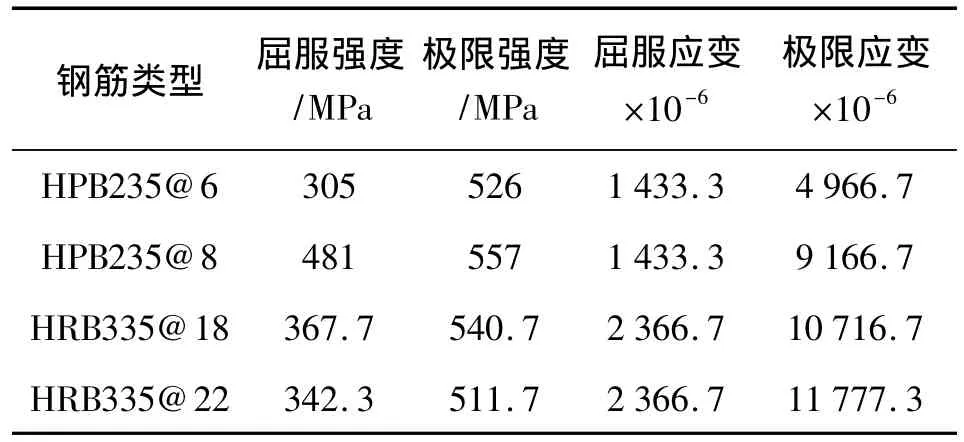
表2 鋼筋受拉強度試驗數據Table 2 Test data on the tensile strength of reinforcing bars

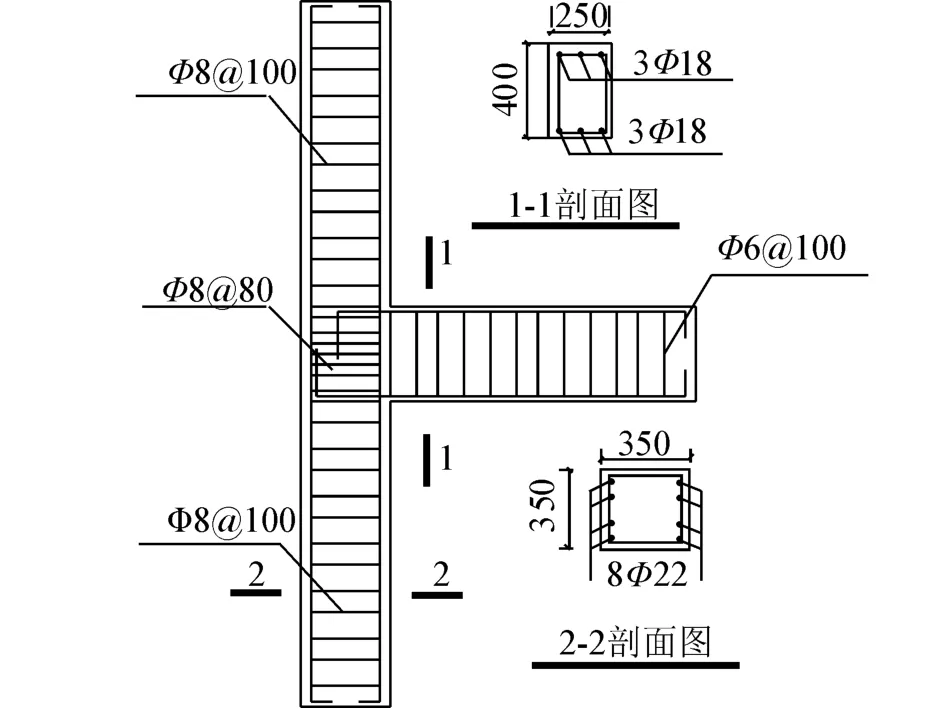
圖1 梁柱邊節點配筋圖Fig.1 Schematic diagram of reinforcement of the exterior beam-column joint

1.2 加載制度及加載設備

試驗采用電液伺服控制系統對試件進行動靜態加載。柱頂采用最大噸位為200 t的作動器通過荷載控制對柱身施加固定軸壓力，柱頂通過與加力架連接的鋼支撐固定以保證節點組合體平面內外的穩定性，柱底安放球鉸。梁端作動器通過位移控制施加往復荷載，作動器與梁端通過連接件連接，可實現往復拉壓。試驗加載裝置簡圖如圖2所示。

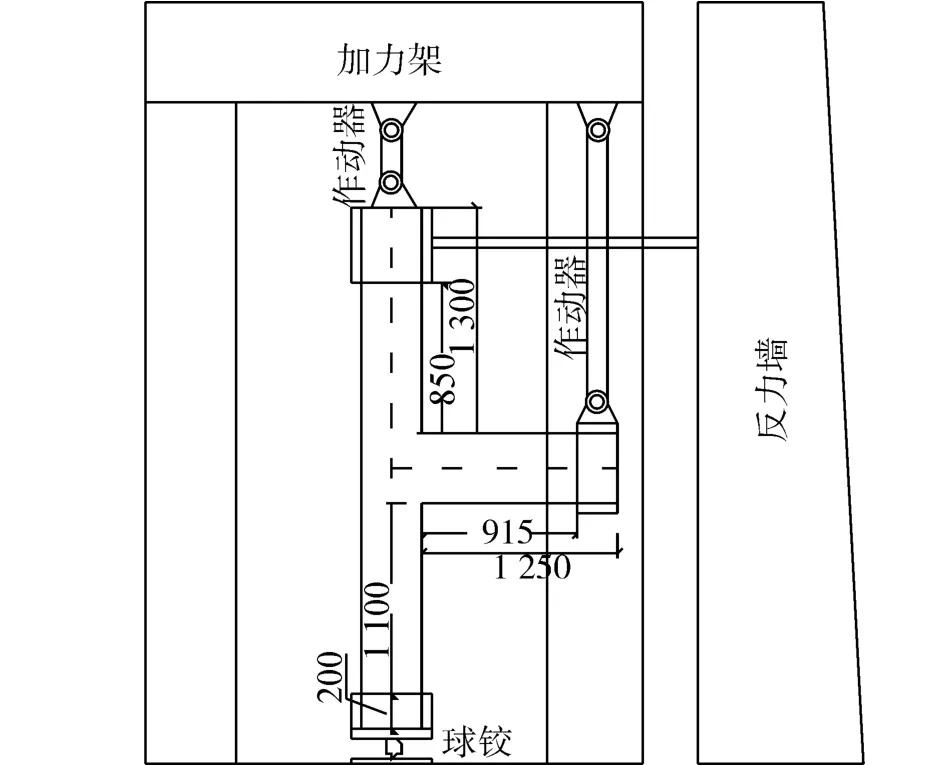
圖2 加載裝置Fig.2 Schematic diagram of the loading equipment

試件JM1-1a、JM1-1b、JM1-1c的軸壓比分別為0.05、0.1、0.05，梁端加載速度分別為0.4、0.4、40 mm/s。通過ABAQUS有限元軟件模擬，得到單調靜態加載下，梁端屈服位移為10 mm左右。由此確定試驗加載制度為:先在柱頂按照相應軸壓比施加軸向壓力，該軸向壓力加載到最大值需要20 s，試驗過程中軸力保持恒定不變，預壓(消除變形誤差等)60 s后，梁端按照位移控制變幅往復加載，幅值5、10 mm各循環一次，然后以 10 mm的倍數(20 mm、30 mm、...)加載，每個位移水平下循環2次，直到試件承載力下降至最大承載力的85%以下或者發生最終破壞為止。

2 試驗現象及理論分析

2.1 理論分析

基于經典桁架模型理論而發展起來的軟化拉－壓桿模型，可以用于混凝土結構中應力紊亂區的抗剪設計。該模型滿足平衡方程、協調條件以及本構關系［12-13］。圖3為軟化拉－壓桿模型中梁柱邊節點的抗剪機構。該抗剪機構由斜向機構、水平機構和豎向機構3部分構成。

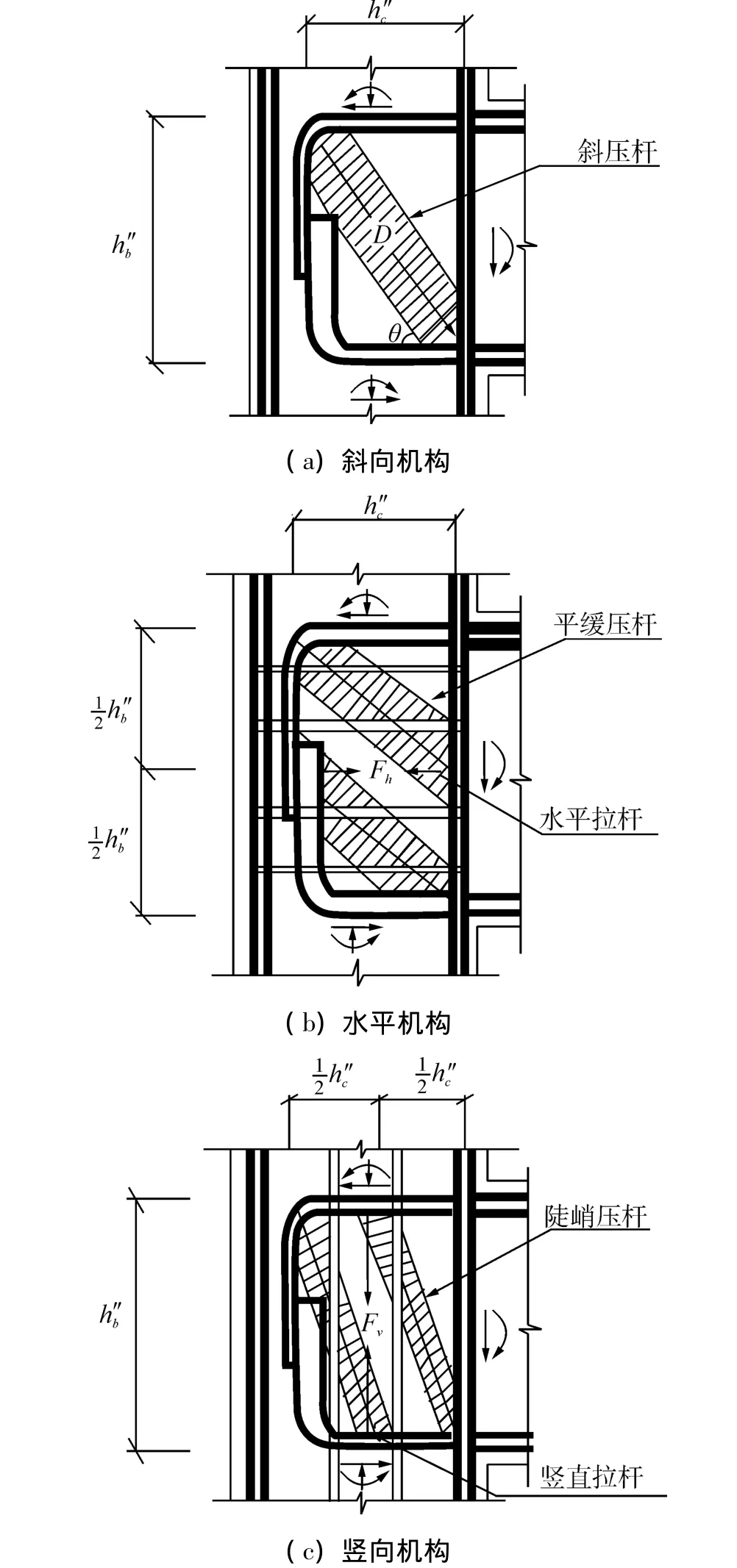
圖3 邊節點抗剪機構Fig.3 Exterior joint shear resisting mechanisms

試驗所采用的試件，柱側面中沒有構造筋，水平剪力只能由斜向機構和水平機構承擔。斜壓桿傾角定義為［12-13］

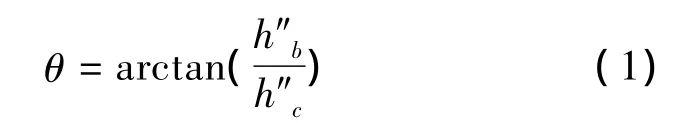
式中:h″b為梁內最外層縱筋之間的距離，h″c為柱內最外層縱筋中心線到最外層梁縱筋彎折部分中心線的距離。由式(1)可得θ=55.9°。此時水平拉桿的拉力與節點水平剪力的比值為［12－13］

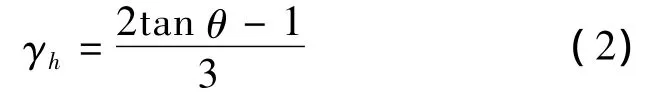
代入斜壓桿傾角，得γh=0.65。水平剪力Vjh作用下，水平拉桿的拉力Fh和斜壓桿的壓力D分別為［12-13］

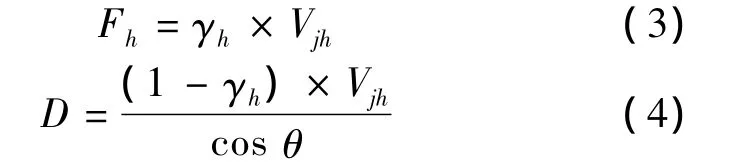
代入γh=0.65，可得Fh=0.65Vjh，D=0.62Vjh。

對于中等延性鋼筋混凝土結構，梁端位移延性系數可取4.0～6.0［14］。為與試驗試件的延性保持一致，此處近似取4.0。文獻［15］指出，梁破壞時曲率延性系數可按下式計算:

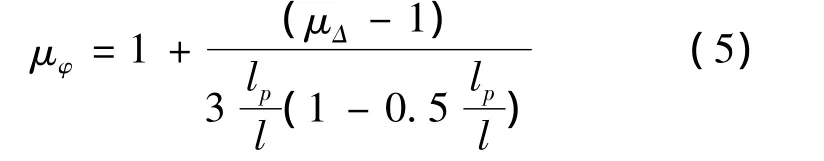
式中:μφ為梁的曲率延性系數;μ△為梁端位移延性系數;lp為梁的塑性鉸長度，計算方法見文獻［15］;l為梁最大彎矩截面到反彎點之間的距離。

反復荷載作用下，曲率延性系數與混凝土受壓區高度的關系為［15］

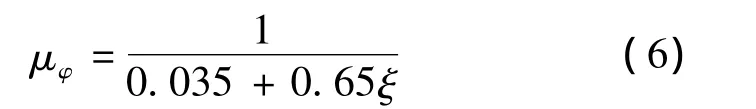
聯立式(5)、(6)得，梁相對受壓區高度ξ近似取0.2。由此可得梁的受壓區高度ab=0.2 h0。軟化拉－壓桿模型中，柱的受壓區高度可近似計算為［11-12］

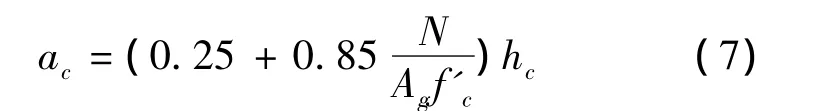
式中:N為柱承受的軸壓力，f'c為混凝土圓柱體標準試件的抗壓強度，Ag為柱毛截面面積，hc為加載方向上柱截面高度。斜壓桿寬度bs取節點的有效寬度，斜壓桿高度as為［12-13］

相應的斜壓桿有效面積Astr為［12-13］

根據式(7)～(9)，得到斜壓桿的極限承載力D=f'c×Astr=985.99 kN。由于節點內部箍筋應力分布不均勻，文獻［12］指出，計算水平拉桿面積時，節點核心區中心處箍筋取全截面面積，其他部分箍筋面積取一半。從而可得水平拉桿的極限承載力Fh= 2×(1+5×0.5)fs×As=196.12 kN。比較發現，斜壓桿的極限承載力遠大于水平拉桿的極限承載力。

混凝土的開裂強度與混凝土圓柱體抗壓強度的關系為［16］

斜壓桿的開裂荷載Dcr=fcr×Astr=69.92 kN，水平拉桿的屈服荷載 Fhy=2×(1+5×0.5)fy×As= 169.36 kN。水平拉桿屈服前，水平拉桿承擔的水平剪力較大，因此斜壓桿在水平拉桿屈服后，才能發生破壞。水平拉桿屈服后，由于軟化拉－壓桿模型中的抗剪機構是超靜定機構，斜壓桿可以繼續承載，節點內的水平剪力主要由斜壓桿承擔。理論分析可知，箍筋屈服前，節點核心區產生的第1條裂縫，位于斜壓桿區域內。試驗測得節點核心區產生裂縫時，中間箍筋的應變為655×10－6，該值小于箍筋的屈服應變1 433.3×10－6。

2.2 試驗現象

試件破壞形態如圖4所示。對試件JM1-1a進行慢速加載。Δ=5 mm時，試件內沒有裂縫產生; Δ=10 mm時，梁內產生彎曲垂直裂縫及剪切斜裂縫;Δ=20 mm時，節點核心區產生第1條斜裂縫，且該斜裂縫位于斜壓桿區域內;Δ=20 mm后的循環，梁內裂縫繼續增多，靠近節點核心區的梁端形成塑性鉸，混凝土被壓碎剝落。

圖4 試件的破壞形態Fig.4 Failure patterns of the specimens

節點組合體最終因梁塑性鉸區域過大變形而發生破壞，如圖4(a)所示。軸壓比增大后，試件JM1-1b的破壞形態沒有明顯不同，如圖4(b)所示。但軸壓比增大后，節點內裂縫數量減少，核心區裂縫的開展受到遏制，節點核心區斜裂縫與水平方向的夾角增大。此外，軸壓比增大后，試件損傷嚴重部分發生轉移。加載速率增大后，試件JM1-1c的破壞形態沒有發生變化，如圖4(c)所示。由于微裂縫的產生和發展過程對加載速率具有敏感性［17］，并且快速加載時，粘結應力分布更加局部［18］。加載速率提高后，試件斷裂面上，有越來越多的骨料被拉斷。并且，裂縫數量不斷減少，損傷基本上是由單一寬裂縫引起的。梁端塑性鉸區損傷更加嚴重，節點核心區損傷相對減弱。

3 試驗結果

3.1 荷載－位移滯回曲線

梁端荷載－位移滯回曲線，如圖5所示，滯回曲線均呈“捏攏”形狀，表明試件受到一定程度剪切變形的影響。

圖4 邊節點荷載－位移滯回曲線Fig.4 The load-deflection hysteresis curve of exterior beam-column joint

3.2 抗剪承載能力

梁柱邊節點受力簡圖，如圖6所示。梁端施加往復荷載F，相應柱端水平剪力為

式中:F為梁端荷載，L為梁端加載點到柱中心線之間的距離，Hc為柱的高度。節點水平剪力為

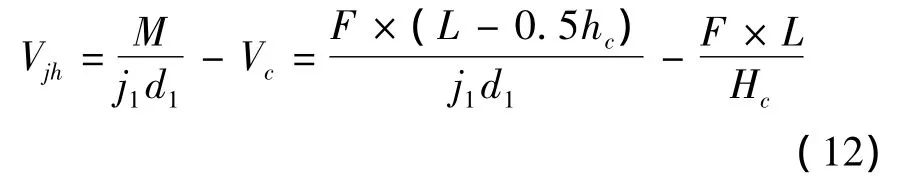
式中:hc為柱截面高度，j1d1為梁截面內力臂。梁端荷載取正反向加載時的平均值，根據試驗結果及式(12)可計算出節點的抗剪承載力，如表3所示。

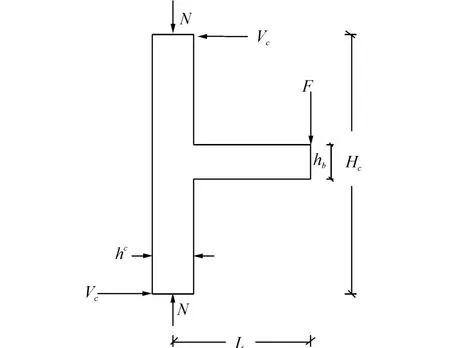
圖6 邊節點受力圖Fig.6 Force diagram of exterior joint specimen

由表3可知，軸壓比增大后，節點的水平抗剪承載力變化不明顯，原因在于，一方面軸壓比增大后可以增大斜壓桿的高度;另一方面，軸壓比增大后，斜壓桿與水平方向夾角變大，斜壓桿所提供的水平分力變小。與試件JM1-1a相比，試件JM1-1c的水平抗剪承載力增大了9.73%，說明加載速率提高后，節點的水平抗剪承載力增大。這與試驗中越來越多的骨料被拉斷，以及微裂縫的“遲滯作用”有關。

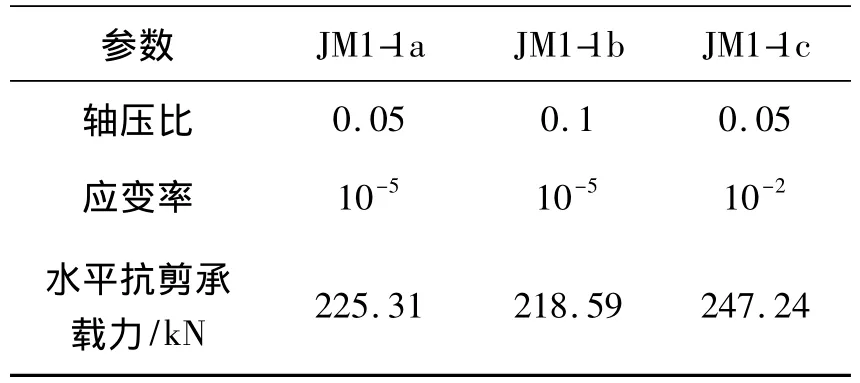
表3 梁柱邊節點水平抗剪承載力Table 3 Horizontal shear carrying capacity of exterior beam-column joints

3.3 位移延性

定義位移延性系數為μΔ=Δu/Δy，屈服位移與極限位移的定義見文獻［15］。通過荷載-位移滯回曲線，可以求得各試件的位移延性系數，如表4所示。由此可見，加載速率或軸壓比提高后，節點組合體的延性降低。變形能力減弱。

表4 梁柱邊節點位移延性系數Table 4 Displacement ductility coefficient of exterior beam-column joints

4 結論

1)軟化拉－壓桿模型可用于預測節點核心區裂縫的開展。邊節點組合體的破壞形態，不受軸壓比或加載速率的影響。軸壓比或加載速率增大后，節點組合體內的裂縫發展受到抑制，損傷嚴重部分發生轉移。

2)加載速率提高后，節點組合體的水平抗剪承載力提高，軸壓比增大后，節點組合體的水平抗剪承載力變化不明顯。

3)加載速率或軸壓比提高后，節點組合體的延性降低，變形能力減弱。

［1］BISCHOFF P H，PERRY S H.Compressive behaviour of concrete at high strain rates［J］.Material and Structures，1991，24(6):425-450.

［2］ABRAMS D A.Effect of rate of application of load on the compressive strength of concrete［C］//Proceedings of the 20th Conference on ASTM.West Conshohocken，USA: ASTM，1917:366-377.

［3］MALVAR L J，ROSS C A.Review of strain rate effects for concrete in tension［J］.ACI Materials Journal，1998，95 (6):735-739.

［4］中國水電水利科學研究院.DL 5073-2000，水工建筑物抗震設計規范［S］.北京:中國電力出版社，2001.

［5］MANJOINE M J.Influence of rate of strain and temperature on yield stresses of mild steel［J］.Journal of Applied Mechanics，1944，11:211-218.

［6］KNOBLOCH M，PAULI J，FONTANA M.Influence of the strain-rate on the mechanical properties of mild carbon steel at elevated temperatures［J］.Materials and Design，2013，49:553-565.

［7］MUTSUYOSHI H，MACHIDA A.Properties and failure of reinforced concrete members subjected to dynamic loading［J］.Transactions of the Japan Concrete Institute，1984，6: 521-528.

［8］ADHIKARY S D，LI B，FUJIKAKE K.Dynamic behavior of reinforced concrete beams under varying rates of concentrated loading［J］.International Journal of Impact Engineering，2012，47:24-38.

［9］LAMARCHE C P，TREMBLAY R.Seismically induced cyclic buckling of steel columns including residual-stress and strain-rate effects［J］.Journal of Constructional Steel Research，2011，67(9):1401-1410.

［10］BHOWMICK A K，DRIVER R G，GRONDIN G Y.Seismic analysis of steel plate shear walls considering strain rate and P-delta effects［J］.Journal of Constructional Steel Research，2009，65(5):1149-1159.

［11］UNAL M，BURAK B.Development and analytical verification of an inelastic reinforced concrete joint model［J］.Engineering Structures，2013，52:284-294.

［12］HWANG S J，LEE H J.Analytical model for predicting shear strengths of exterior reinforced concrete beam-column joints for seismic resistance［J］.ACI Structural Journal，1999，96(5):846-857.

［13］HWANG S J，LEE H J.Analytical model for predicting shear strengths of interior reinforced concrete beam-column joints for seismic resistance［J］.ACI Structural Journal，2000，97(1):35-44.

［14］傅劍平.鋼筋混凝土框架節點抗震性能與設計方法研究［D］.重慶:重慶大學，2002:88-208.

FU Jianping.Seismic behaviour and design of Joints in a reinforced concrete frame［D］.Chongqing:Chongqing U-niversity，2002:88-208.

［15］趙國藩.高等鋼筋混凝土結構學［M］.北京:機械工業出版社，2005:383-387.

［16］BELARBI A，HSU T T C.Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete［J］.ACI Structural Journal，1994，91(4):465-474.

［17］閆東明，林皋，王哲，等.不同應變速率下混凝土直接拉伸試驗研究［J］.土木工程學報，2005，38(6):97-103.

YAN Dongming，LIN Gao，WANG Zhe，et al.A study on direct tensile properties of concrete at different strain rates［J］.China Civil Engineering Journal，2005，38(6):97-103.

［18］TAKEDA J I.Dynamic fracture of concrete structures due to severe earthquakes and some consideration on countermeasures［C］//Proceedings of the 8th World Conference on Earthquake Engineering.San Francisco，USA，1984: 299-306.