應用TFLS算法尋找SBEGN模型具最多葉子生成樹

王曉敏，趙喜楊，姚 兵

（西北師范大學 數學與統計學院，甘肅 蘭州 730070）

0 引 言

現實世界中的自然、社會和科學系統均以網絡的形式存在，而且這些網絡大多數具有無標度性或小世界性，或者二者皆有［1－3］.當今的復雜網絡理論已成為很多學科發展的新視角和指導思想，如疾病傳播［4］.近年來一個活躍的研究課題是試圖運用生成樹來刻畫復雜網絡，從生成樹這一全新的視角出發，對復雜網絡的拓撲結構、物理意義和數學特性進行深入、廣泛的研究.新方法已在金融、生理醫學、生物等自然科學或社會科學領域得到深入淺出的探討.

通常，復雜網絡中含有很多的葉子，所以在網絡的結構研究中自然而然地使用了生成樹，使得生成樹能夠廣泛地用于網絡研究.例如，無線傳感器網絡的生成樹最大限度地提高了鏈路的質量度量的總和，并提供了與所有節點對之間的最短的最弱鏈路的路徑［5］.生成樹的最典型的應用之一是：Perlman［6］利用生成樹與網絡間的結構關系發明了廣泛用于網橋、交換機上的生成樹協議，以及各種使用路由算法的鏈路狀態機制.應用生成樹在復雜網絡中實現有效的搜索也是研究網絡的一個重要的課題.例如：生成樹被應用于網絡的搜索算法［5］.復雜網絡搜索的早期例子：著名的“六度分離”實驗在一定程度上揭示了實際網絡的可搜索性.Kleinberg［7］首先在理論上研究了復雜網絡的搜索能力，即在網絡中實現快速搜索的性質；之后Kleinberg、Watts、Adamic等［8］針對各自的特定模型提出了對應的搜索算法.值得注意的是，關于無標度生成樹的研究報道很少［9］，理解或給出網絡模型的無標度生成樹的文章幾乎見不到.

為更好地理解和認識復雜網絡，學者們經常采用建立動態網絡模型來逼近和模擬現實網絡.本文借用相似于文獻［3］的構造網絡模型的方法，采用初始網絡為一般的連通網絡，并使得新進入網絡的節點多于一個，從而構造出本文的研究對象SBEGN 模型.不難觀察到，新發表的文章更傾向于引用一些被廣泛引用的重要文獻，新的個人主頁上的超文本鏈接更有可能指向著名的站點，與強者恒強、弱者恒弱的網絡現象相吻合.受這些網絡現象的啟發，本文設計時間優先層次搜索算法來尋找具有最多葉子的生成樹，以期用算法優化研究網絡的生成樹，提高網絡的搜索效率，減少網絡的運算量，為尋找實際網絡模型的生成樹提供理論幫助.本文所考慮的圖均為有限、無向簡單圖，沒有定義的術語和符號均源于文獻［10］.對于一個圖G，它的葉子節點的集合用記號L（G）表示，nd（G）表示圖G中度數為d的頂點的個數.記號｜X｜表示集合X的元素個數.

1 SBEGN模型的建立及其基本性質

對任意給定的至少有2 個節點的連通網絡N（0），用d1，d2，…，da表示連通網絡N（0）不同的度，且 滿 足d1＞d2＞… ＞da.初 始 網 絡 為N（0），用記號nv（0）和ne（0）分別表示它的節點個數和邊數目，記號V（0）和E（0）分別表示初始網絡N（0）的節點集合和邊集合，使得nv（0）＝｜V（0）｜，ne（0）＝｜E（0）｜.對于初始網絡N（0）的每一條邊界邊uv∈E（0），新增加m個節點，并且將這m個節點與邊uv的端點u、v分別相連，產生t＝1時刻的網絡N（1），并將最后一個新節點w與節點u、v分別相連所得的2條邊wu和wv定義為網絡N（1）的邊界邊.記號X1代表給N（0）新增加的節點集合，Y1代表給N（0）新增加的邊集合，則有Y1＝｛wu，wv：uv∈E（0），w∈X1｝，以及V（1）＝V（0）∪X1，E（1）＝E（0）∪Y1，｜Y1｜＝2｜X1｜＝2mne（0）.

類似地，對于網絡N（1）的每條邊界邊xy∈E（1），新增加m個新節點，并且將這m個節點分別與邊xy的端點x、y相連，從而得到t＝2時刻的網絡N（2），并將最后一個新節點z與節點x、y分別相連所得的2 條邊zx和zy定義為網絡N（2）的邊界邊.顯然，N（2）的節點集合可表示為V（2）＝V（1）∪X2，它的邊集合為E（2）＝E（1）∪Y2.以此類推，按照上述構造方法，從網絡N（t－1）可得到網絡N（t），簡稱它為SBEGN 模型.下面給出SBEGN 模型N（t）的一些基本參數.記號Xk和Yk分別表示給N（k－1）新增的節點集合和邊集合.當t≥1時，SBEGN 模型N（t）的節點集合V（t）與邊集合E（t）可以分別表示為

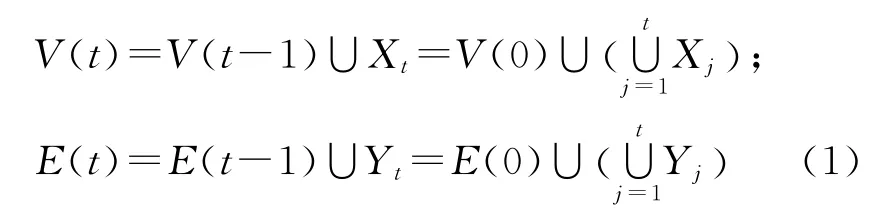
因為

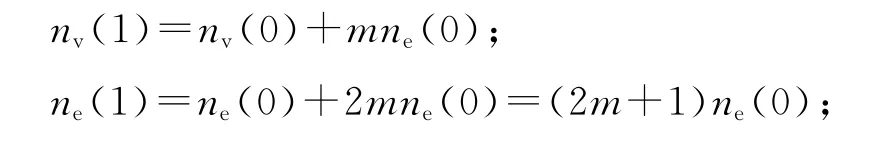
不難得到SBEGN 模型N（t）的節點數目和邊數目

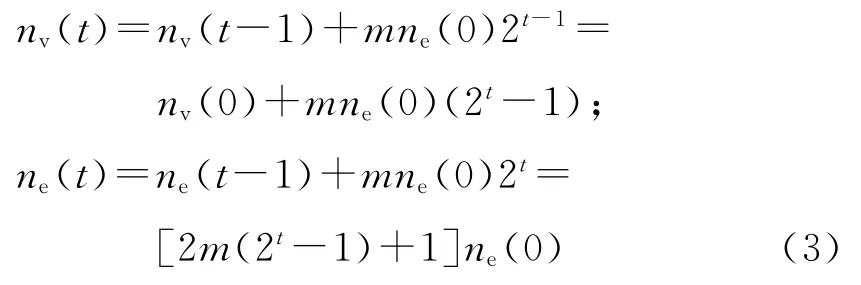
此外，SBEGN 模型N（k）的新增加節點數目為

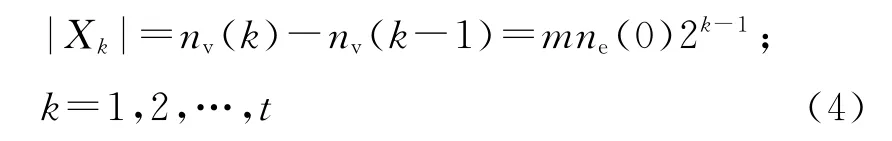
且有ne（0）2k條邊界邊，在SBEGN 模型N（t）中，最大度Δ（N（t））＝（tm＋1）·Δ（N（0）），最小度δ（N（t））＝2.則SBEGN 模型是一個稀疏網絡，因為它的平均度〈k〉滿足

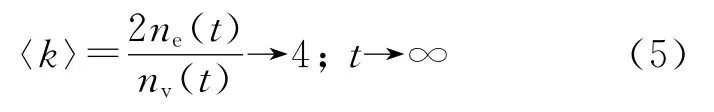
式（3）表明SBEGN 模型N（t）具有優先鏈接性，即新進入N（t）的節點與初始網絡N（0）中的節點相連的概率較大.同時，N（t）的構造表明N（t）具有增長性，說明N（t）屬于BA 無標度模型［3－4］.

以 下 用k（u，i）表 示 于 時 刻i節 點u在SBEGN 模型N（i）中所連接的邊數目，用kt（u，i）表示節點u在N（i）中的具有最多葉子生成樹中所連接的邊數目.

為證明SBEGN 模型N（t）是層次網絡，下面估算N（t）的每個節點的聚集系數.

（1）對初始網絡N（0）的節點u∈V（0），設k（u，0）＝dj，那么，這個節點u在N（t）中的鄰點的個數也就是它的度數，且k（u，t）＝（1＋tm）dj.記號Eu表示節點u的鄰點之間的邊集合，按照SBEGN 模型N（t）的構造，可計算出Eu的元素個數為｜Eu｜＝（1＋tm）dj.按照定義，節點u的聚集系數為

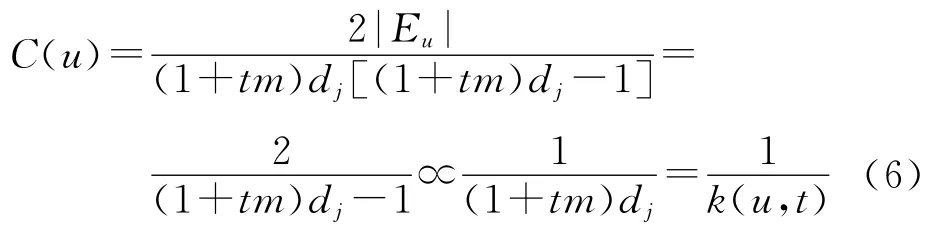
（2）對在i（＜t）時刻進入網絡N（i）的節點v，且節點v又是N（i＋1）的一條邊界邊的端點，那么，在N（t）中，節點v的度數為k（v，t）＝2［（ti）m＋1］，它的鄰點之間的邊集合Ev有2（t－i）m＋1個元素.節點v的聚集系數為

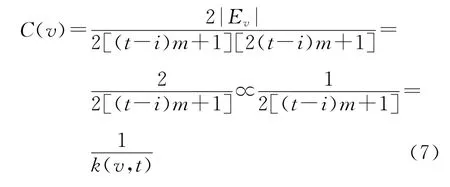
（3）對在j（＜t）時刻進入網絡N（j）的節點w，且節點w又不是N（j＋1）的一條邊界邊的端點，則在N（t）中它的度數為k（w，t）＝2，它的鄰點之間的邊集合Ew僅有一個元素，所以

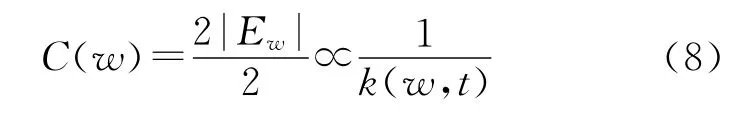
按照文獻［11］和［12］的定律，上述式（6）～（8）關于節點聚集系數分布的式子證明SBEGN模型是層次網絡，且對任何時刻t成立，即SBEGN 模型與好萊塢的演員網、WWW、代謝網絡等屬于同一類網絡［12］，從而為本文的時間優先層次搜索算法提供了理論依據.圖1給出SBEGN 模型的例子.

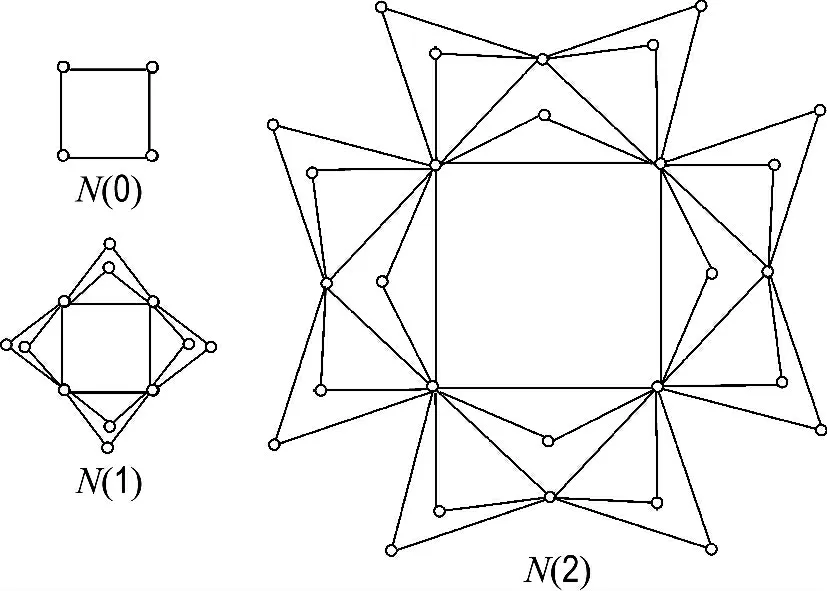
圖1 當m＝2時，SBEGN 模型的N（0）、N（1）及N（2）Fig.1 N（0），N（1）and N（2）of SBEGN models when m＝2

2 SBEGN 模型的生成樹

SBEGN 模型N（t）的生成樹是一個連通且邊數目最少的子網絡，本章尋找N（t）的具有最多葉子的生成樹.一般情形下，N（t）的具有最多葉子的生成樹是不唯一的.用L（TM（t））表示N（t）的具有最多葉子的生成樹TM（t）的全體葉子的集合.SBEGN 模型N（t）的生成樹TM（t）具有如下的性質：

引理1 SBEGN 模型N（t）的任意一棵具有最多葉子的生成樹TM（t）的葉子集合完全包含新進入N（t－1）的節點集合Xt.

證明 對任意時刻t≥1，假設存在節點w∈Xt，但wL（TM（t））.根據SBEGN 模型N（t）的構造，節點w的度數為k（w，t）＝2，且節點w與t－1時刻的SBEGN 模型N（t－1）的一條邊界邊uv的2個端點u和v分別相連.注意到，由于w不是TM（t）的葉子，則節點u和v至少有一個不是TM（t）的葉子，假設節點u不是葉子.則可以構造SBEGN 模型N（t）的另一棵生成樹H如下：在TM（t）中刪除邊wv，連接邊uv.顯然w，v∈L（H），且生成樹H的葉子數目｜L（H）｜≥｜L（TM（t））｜＋1，這違背TM（t）是N（t）的一棵具有最多葉子的生成樹.本引理得證.□

引理2 設N（0）是給定的連通初始網絡.對SBEGN 模型N（t），有

（Ⅰ）當t≥3 和L（TM（1））∩V（0）≠，則L（TM（t））∩V（0）＝.

（Ⅱ）當t≥2 和L（TM（1））∩V（0）＝，則L（TM（t））∩V（0）＝.

證明 為證結論（Ⅰ），假設存在葉子x∈L（TM（t））∩V（0），即L（TM（t））∩V（0）≠，設xy∈E（0），顯然，yL（TM（t））.根據SBEGN 模型N（t）的構造和引理1，存在N（t）的一個2度節點wt，i∈Xt與節點x、wt－1，i∈Xt－1分別相連，則有wt－1，iL（TM（t）），并且wt，i∈L（TM（t））.注意到，節點wt－1，i的度數k（wt－1，i，t）≥3，也就是說，節點wt－1，i與節點x、wt，i、wt－2，i均相連.因為t－2≥3，如果wt－2，i∈L（TM（t）），導致wt，i、wt－1，i與其他節點不連接，這矛盾于TM（t）是樹.下面構造N（t）的 另 一 棵 生 成 樹H＊：刪除邊wt，iwt－1，i和wt－1，iwt－2，i；如果節點x在TM（t）中與節點y連接，將節點x與節點wt，i和wt－1，i分別相連；如果節點x在TM（t）中與節點u（≠y）連接，則刪除邊xu，然后將節點x與節點y連接.此時，｜L（H＊）｜≥｜L（TM（t））｜，矛盾于TM（t）是具有最多葉子生成樹的事實.

結論（Ⅱ）的證明相同于結論（Ⅰ）的證明，故不贅述.□

定理1 當t≥3時，SBEGN 模型N（t）的每一棵具有最多葉子的生成樹TM（t）的葉子數目為

且它的直徑D（TM（t））不超過初始網絡N（0）的具有最多葉子生成樹TM（0）的直徑D（TM（0））加上（2t－1）.

證明 為證明此定理，先給出時間優先層次搜索算法.

時間優先層次搜索算法（time－first levelsearching algorithm），簡稱為TFLS算法.

輸入 一個SBEGN 模型N（t），t≥3.

輸出N（t）的全體具有最多葉子的生成樹TM（t），且每一棵TM（t）帶有一個關于節點的時間序函數p.

步驟1 當k＝1，2時，FM（k）←｛N（k）的全體具有最多葉子的生成樹｝.對每一棵具有最多葉子的生成樹T0∈FM（k），定義V（T0）節點的一個時間序函數p為：若在V（T0）中，節點x的位置前于節點y的位置，則p（x）＜p（y），且有1＝min｛p（x）｜x∈V（T0）｝，｜V（T0）｜＝max｛p（x）｜x∈V（T0）｝.以下記號Nei（x）為與節點x有連線的節點集合.

步驟2s←1若t為奇數，否則s←2.

步驟3 如果s＜t－2，Gs←，到步驟4.如果s＝t－2，到步驟5.

步驟4 若FM（s）＼Gs＝，s←s＋1，到步驟3.否則，取Ts∈FM（s）＼Gs，V″←V（Ts），E″←E（Ts），T″←（V″，E″），Xs←，到步驟4.1.

步驟4.1 如果V（Ts）＼Xs＝，TM（s＋1）←T″；FM（s＋1）←FM（s＋1）∪｛TM（s＋1）｝，Gs←Gs∪｛Ts｝，到步驟4.如果V（Ts）＼Xs≠，到步驟4.2.

步驟4.2 取x∈V（Ts）＼Xs，使得p（x）＝min｛p（y）｜y∈V（Ts）＼Xs｝.若Nei（x）∩（V（s＋1）＼V″）＝，Xs←Xs∪｛x｝，到步驟4.1；否則，到步驟4.3.

步驟4.3Nei（x）∩（V（s＋1）＼V″）＝｛ux，1，ux，2，…，ux，m｝（m≥1），執行：p（ux，1）←p（u′）＋1，u′是V″的最后一個節點，然后把ux，1放進V″的最后 一 個 位 置 上；從j＝2 到m，p（ux，j）←p（ux，j－1）＋1，把ux，j放進V″的最后一個位置上.E″←E″∪｛xy｜y∈V″｝，T″←（V″，E″）；Xs←Xs∪｛x｝，到步驟4.1.

步驟5FM（t）←，F←.

步驟5.1 如果FM（t－2）＼F≠，取Tt－2∈FM（t－2）＼F，由上面的過程，知V（Tt－2）的節點有 一 個 時 間 序 函 數p；VH←V（Tt－2），EH←E（Tt－2），H←（VH，EH）；Xt←，到步驟5.2.如果FM（t－2）＼F＝，到步驟6.

步驟5.2 如果V（Tt－2）＼Xt≠，到步驟5.3；如果V（Tt－2）＼Xt＝，F←F∪｛Tt－2｝，到步驟5.1.

步驟5.3 取x∈V（Tt－2）＼Xt，使得p（x）＝min｛p（y）｜y∈V（Tt－2）＼Xt｝，若Nei（x）∩（V（t）＼V（t－2））＝，Xt←Xt∪｛x｝，到步驟5.2；否則，到步驟5.4.

步驟5.4Nei（x）∩（V（t）＼V（t－2））＝｛vx，1，vx，2，…，vx，n｝（n≥1）.執 行：p（vx，1）←p（u′）＋1，u′是VH的最后一個節點，然后把vx，1放進VH的最后一個位置上；從j＝2到n，p（vx，j）←p（ux，j－1）＋1，把ux，j放進VH的最后一個位置上.EH←EH∪｛xy｜y∈VH｝，H←（VH，EH）.Xt←Xt∪｛x｝.FM（t）←FM（t）∪｛H｝，到步驟5.2.

步驟6 返回FM（t），且FM（t）的每一棵具有最多葉子的生成樹TM（t）帶有一個時間序函數p.

根據引理2，TFLS算法的步驟3中s＝t－2成立.因為SBEGN 模型N（k）中的Xk里有個節點成為N（k）的邊界邊的端點，則在SBEGN 模型N（k＋1）中，這些節點與新增加的節點連線，且當k≥2，它們不可能是TM（k＋1）的葉子.根據TFLS算法，有如下的遞歸公式：

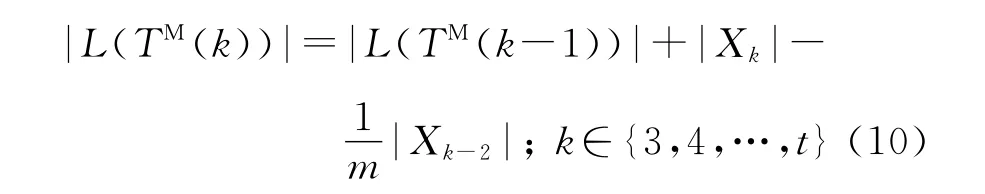
根據｜L（TM（2））｜＝｜X2｜＋｜X1｜，整理得

聯立式（4），可求得｜L（TM（t））｜的精確值為

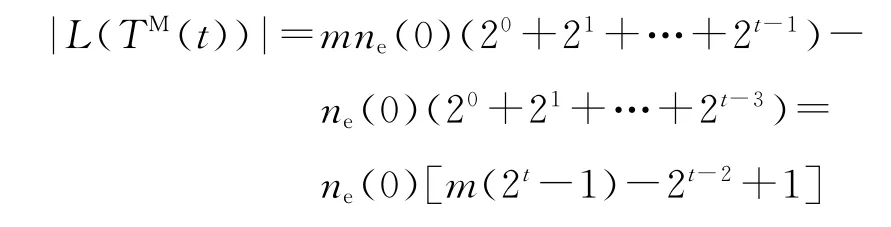
根據TFLS算法找到TM（t）的過程，是每次給TM（t－1）添加葉子得到生成樹TM（t），即給TM（t－1）的最長路徑增加了2.則當t≥3 時，D（TM（t））不超過初始網絡N（0）的具有最多葉子生成樹TM（0）的直徑加上（2t－1）.□

圖2給出用算法找到圖1中SBEGN 模型的3個具有最多葉子的生成樹.

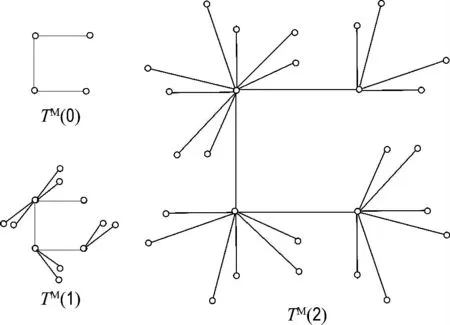
圖2 當m ＝2 時，3棵生成樹TM （0）、TM（1）和TM（2）Fig.2 Three spanning trees TM（0），TM（1）and TM（2）when m ＝2

3 TFLS算法找到的生成樹的性質

由定理1可得出下面2個極限.

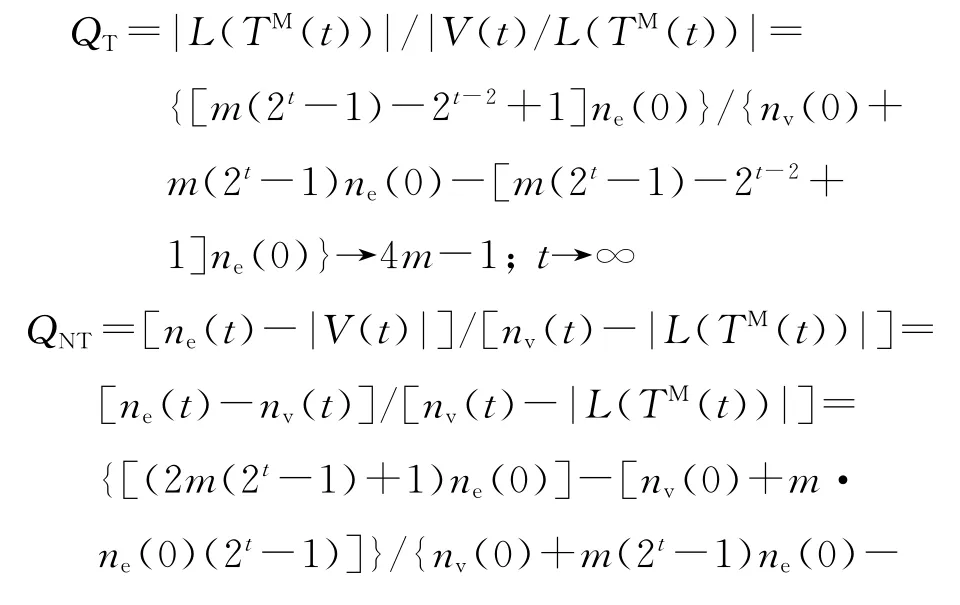
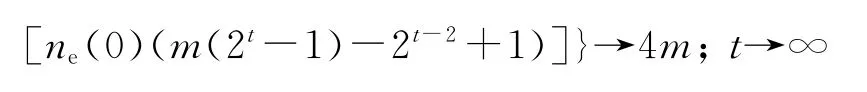
上述兩個極限說明，當時間t足夠大時，比值QT幾乎等價于比值QNT，即QT～QNT.因此可以嘗試用生成樹TM（t）來解釋SBEGN 模型N（t）的一些性質.

下面討論生成樹TM（t）的度譜.前面提到初始網絡N（0）節點不同的度數為d1，d2，…，da，且d1＞d2＞…＞da.TFLS算法找到的生成樹TM（t）的節點數目與度數的度譜在表1中給出，其中t時刻度數為d的節點個數為nd（t），f（di）＝tm（di

表1 TFLS算法找到的生成樹TM（t）的度譜Tab.1 The spectrum of spanning tree TM（t）by applying the TFLS algorithm

由于生成樹TM（t）的度譜是離散型，可以計算它的隨機選擇恰好有k邊的節點的概率P（k）.根據文獻［3］使用的統計技術和式（4），可得下面的式子：

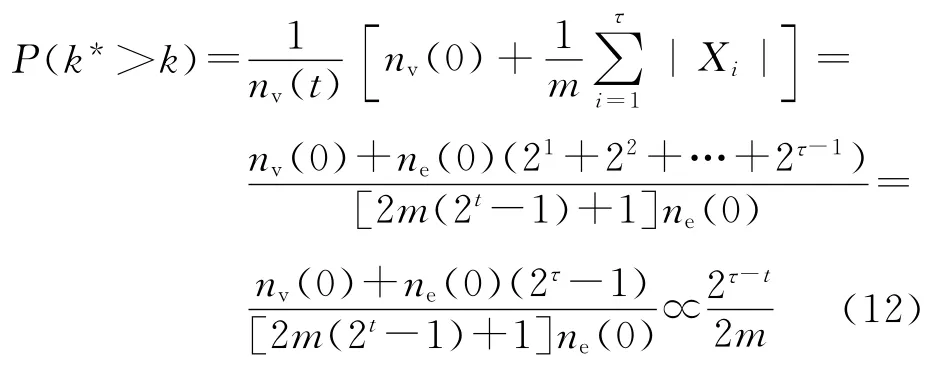
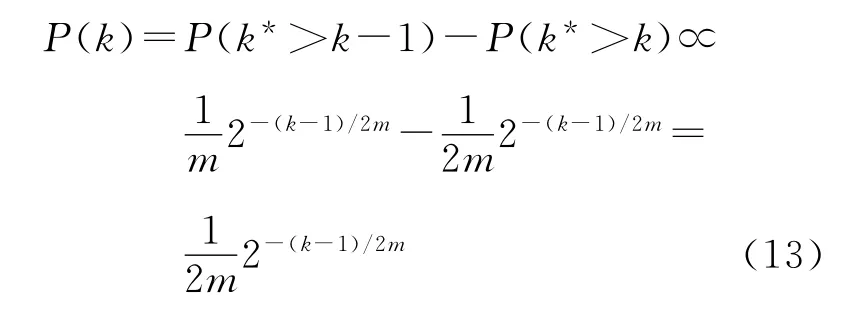
上式說明，最多葉子的生成樹TM（t）服從指數分布，TM（t）亦為指數型生成樹.

在j（＜t）時刻，最多葉子的生成樹TM（j）的頂點數目為｜V（TM（j））｜＝nv（j），則它的累積分布為

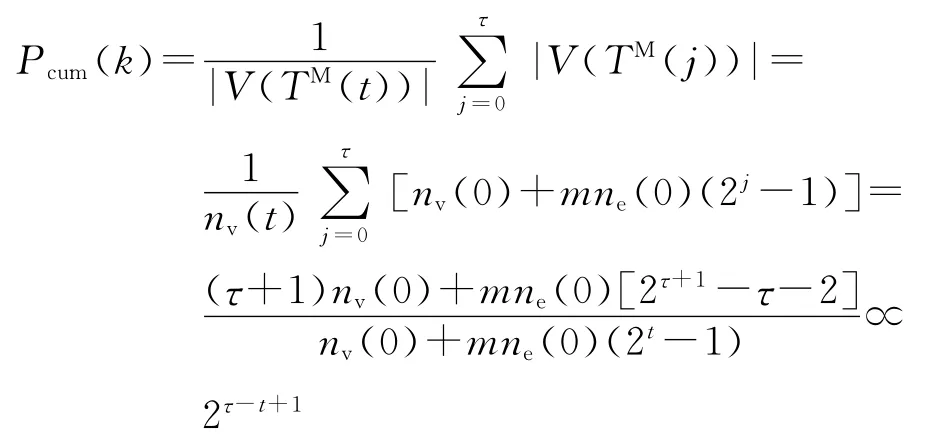
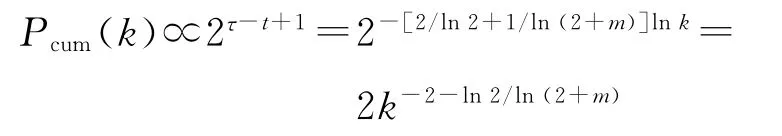
下面再給出關于SBEGN 模型的具有最多葉子的生成樹的結論.

定理2 當t≥3時，SBEGN 模型N（t）的任意2棵具有最多葉子的生成樹TMi（t）和TMj（t）擁有相同的葉子集合，即L（TMi（t））＝L（TMj（t））.

證明 令Li＝L（TMi（t））和Lj＝L（TMj（t））.注意到t≥3，由引理2，Li∩V（0）＝＝Lj∩V（0）.設有u∈Li，但uLj.由于Li∩N（0）＝，不妨設u是給N（k）的邊界邊xy添加的m個節點中的一個.它在Lj中的度數kt，j（u，t）滿足2［（t－k）m＋1］≥kt，j（u，t）≥2，它在N（t）中的度數k（u，t）＝2或k（u，t）＝2［（t－k）m＋1］.

情形1 如果u不是N（k＋1）的任何邊界邊的端點，則它在N（t）中的度數k（u，t）＝2，故kt，j（u，t）＝1.構造N（t）的另一棵生成樹H＝Lj－uy＋xy，即在Lj中刪去邊uy，然后將x和y連接.顯然，｜L（H）｜＞｜L（TMj（t））｜，矛盾.這是由于u是H的葉子，而Lj的其他節點的屬性在H中沒有發生變化.

情形2 如果u是N（k＋1）的邊界邊的端點，那么，度數kt，j（u，t）≥3，且它在N（t）中的度數為k（u，N（t））＝2［（t－k）m＋1］.根據上面節點u∈Li的屬性，在N（t）中，節點x和u與節點x1，x2，…，xm均相連，節點y和u與節點y1，y2，…，ym均相連.根據引理1和u∈Li，得xr，yr∈Li，r＝1，2，…，m.因為t≥3，則在N（t）中，有度數k（x，t）≥2和k（y，t）≥2.根據引理2，xLi和yLj.對TMj（t）實施如下運算：刪去邊uy將x與y連接，然后對r＝1，2，…，m，將xr與x連接，將yr與y連接，得到新的生成樹H′.由于u∈L（H′），而且TMj（t）的其余節點的屬性在H′中沒有發生變化，也就是說｜L（H′）｜＞｜L（TMj（t））｜，這與TMj（t）是最多葉子生成樹的假定矛盾.

綜合上述2種情形的推證，L（TMi（t））＝L（TMj（t））.□

由于SBEGN 模型是層次網絡，運用以上結論不難證明：當t≥3時，SBEGN 模型N（t）的一棵具有最多葉子生成樹TM（t）包含次一級SBEGN 模型N（t－1）的一棵具有最多葉子的生成樹TM（t－1）.

4 結 語

本文構造了SBEGN 模型N（t），并設計了時間優先層次搜索算法，隨后找出SBEGN 模型N（t）的具有最多葉子的生成樹TM（t），確定了任何具有最多葉子的生成樹的拓撲性質.需要指出的是，本文的SBEGN 模型具有良好的性質：當t≥3時，N（t）的任意2棵具有最多葉子的生成樹TMi（t）和TMj（t）擁有相同的葉子集合，且N（t）為層次網絡，它的直徑小于生成樹TM（t）的直徑，換句話說，N（t）是小世界網絡模型.這些良好的性質不僅為實際網絡建設提供了可靠的理論依據，更重要的是為模擬實際網絡提供了易于理解和掌握的工具，并不斷產生優化型算法.作為進一步研究的方向，將考慮模型的隨機增加連線或者隨機刪除連線，這樣的研究對實際網絡的模擬會更有價值.顯然，確定這種網絡模型的拓撲性質以及找到它們的具有最多葉子的生成樹將是研究的關鍵，也是研究的難點.

［3］ ZHANG Zhong－zhi，RONG Li－li，GUO Chong－hui.A deterministic small－world network created by edge iterations［J］.Physica A：Statistical Mechanics and its Applications，2006，363（2）：567－572.

［4］ Pastor－Satorras R，Vespignani A.Epidemic spreading in scale－free networks ［J］.Physical Review Letters，2001，86（14）：3200－3203.

［5］ ZHENG Geng－zhong，LIU San－yang，QI Xiaogang.Scale－free topology evolution for wireless sensor networks with reconstruction mechanism［J］.Computers and Electrical Engineering，2012，38（3）：643－651.

［6］ Perlman R.Hierarchical networks and the subnetwork partition problem ［J］.Computer Networks and ISDN Systems，1985，9（4）：297－303.

［7］ Kleinberg J.The small－world phenomenon：An algorithmic perspective［C］／／Proceedings of the 32nd Annual ACM Symposium on Theory of Computing，STOC 2000.New York：Association for Computing Machinery，2000：163－170.

［8］ Adamic L A，Adar E.How to search a social network［J］.Social Networks，2005，27（3）：187－203.

［9］ Kim Dong－hee，Noh Jae－dong，Jeong Ha－woong.Scale－free trees：The skeletons of complex networks［J］.Physical Review E—Statistical Nonlinear，and Soft Matter Physics，2004，70（42）：046126.

［10］ Bondy J A，Murty U S R.Graph Theory with Applications ［M］.Amsterdam：North Holland，1976.

［11］ Dorogovtsev S N，Goltsev A V，Mendes J F F.Pseudofractal scale－free web ［J］.Physical Review E—Statistical Nonlinear，and Soft Matter Physics，2002，65（6）：066122.