隨機變量非正態分布且相關的機械零件單模失效可靠度分析

劉華漢，蔣 瑋，楊光輝，呂海霆

（大連理工大學 機械工程學院，遼寧 大連 116024）

0 引 言

機械產品的可靠性設計不同于電子產品可靠性設計.對機械系統來說有3種不同形式的相關性問題：一是考慮引起零件單模失效的隨機變量相關性問題，二是考慮零件失效模式之間相關性問題，三是機械系統零件間的相關性問題.而對于機械系統中單個零件的可靠度分析，應充分考慮上述前兩種相關性問題.目前的研究工作集中在零件失效模式間相關性問題及機械零件（單模失效）間的相關性問題［1－10］的研究方面，而對于機械零件隨機變量相關的單模失效問題的研究鮮有報道.

機械零件可靠度計算的基本理論為應力－強度干涉理論（又稱為應力－強度相干模型），在以往的文獻中，此理論都是在應力和強度完全獨立的情況下導出的，但實際上并不是所有的零件可靠性問題中的應力和強度完全獨立，例如軸系零件設計變量的荷載、強度等因素之間存在程度不同的相關性［11］.同時，在需要考慮構件的自重時，構件的應力和強度之間也存在相關性［12］.喻天翔等［13］通過非線性變換，建立了僅考慮應力、強度兩個隨機變量相關時的零件單模失效可靠度模型，并探討了相關系數對零件單模可靠度的影響及相對誤差，但假設隨機變量的分布都為正態分布且只考慮應力、強度兩個變量相關.

引起機械零件廣義應力與強度隨機性的因素主要有材料、加工、制造、安裝、荷載等，如同種材料性能分布的不均勻、制造精度誤差.正是由于這些參數的隨機性才有了可靠度的概念.要想得到這些因素的實際隨機性參數是比較困難的，因此在理論分析中常常假設這些因素服從常見的分布，如正態分布、威布爾分布、指數分布等.現有的大多數文獻中假設隨機參數服從正態分布，但很多情況下并非如此.這時就需要探求隨機變量因素服從其他分布時的可靠度計算公式，探求將非正態分布轉化為正態分布的方法，利用正態分布運算的成熟的計算技術來求得零件可靠度.

本文針對引起機械零件單模失效的隨機變量為不相關正態隨機變量、相關正態隨機變量、不相關非正態隨機變量、相關非正態隨機變量4種情況，借鑒結構可靠性求解理論，尋求建立機械零件單模失效可靠度求解模型的統一方法.主要是建立相關非正態隨機變量的可靠度求解理論模型.不相關正態隨機變量的可靠度理論是求解其他3種情況的基礎.最后，通過齒輪傳動的實例說明本文所提方法的有效性.

1 零件單模失效可靠度求解統一模型建立

全面考慮引起機械零件單模失效的各個因素：隨機變量是否服從正態分布，隨機變量之間是否具有相關性，隨機變量之間是否為線性關系.機械零件單模失效可靠度求解統一模型框圖如圖1所示.設零件單模失效的極限狀態方程為M＝G（X），其中X＝（X1X2…Xn）T為隨機變量，它們共同影響失效狀態函數中的應力強度.這些隨機變量中可能含有非正態隨機變量，各個隨機變量之間可能存在相關性.下面將對統一模型由簡單到復雜展開說明.

圖1 機械零件單模失效可靠度模型Fig.1 Single failure mode reliability model of the mechanical components

1.1 隨機變量正態分布不相關時零件單模可靠度求解理論

此為求解零件可靠度最簡單也是基礎的模型，如圖1中Ⅰ框所示，計算步驟如下：

步驟1 正態隨機變量正則化為標準正態隨機變量.

假設影響極限狀態方程的隨機變量為Y＝（Y1Y2…Yn）T，極限狀態方程為

其中Yi～N（μi，σ2i），各隨機變量不相關，通過式（2）正則化為標準正態隨機變量Z＝（Z1Z2…Zn）T，則極限狀態方程轉化為式（3）的形式：

步驟2 零件單模可靠度的求解.

將極限狀態方程（1）以正則化后的標準正態隨機變量表示為式（3），則式（3）分為兩種情況：隨機變量Zi的線性組合或非線性組合，下面分別表述：

（1）若極限狀態方程（3）為n維標準正態隨機變量Zi的線性組合：

可靠度指數

可靠度

（2）若極限狀態方程（3）為非線性組合，則可采用兩種方法求解.

①一 次 二 階 矩（first－order second－moment，FOSM）法［17］.

將式（3）在平均值處一階泰勒展開，僅保留一階項：

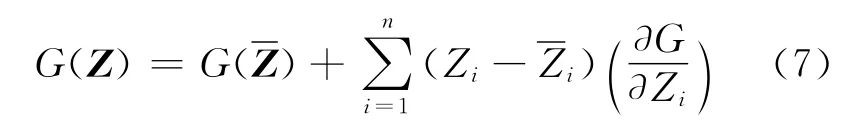
則

零件單模可靠度可由式（5）、（6）求得.

②改進的一次二階矩（advanced first－order second－moment，AFOSM）法［18］.

通過求解式（9）得到可靠度指數β，代入式（6）求得可靠度.對于式（9）的求解可以采用Lagrange乘子迭代法導出的公式進行迭代計算，將在2.1中詳細介紹.

1.2 隨機變量正態分布相關時零件單模可靠度求解理論

假設影響極限狀態方程的隨機變量為X＊＝（X＊1X＊2…X＊n）T，極限狀態方程為

步驟1 正態隨機變量正則化為標準正態隨機變量.

按照式（2）、（3）的形式將相關的非標準正態隨機變量X＊＝（X＊1X＊2…X＊n）T正則化為相關的標準正態隨機變量Y＊＝（Y＊1Y＊2…Y＊n）T，然后根據下述步驟2、步驟3進行零件單模可靠度的求解.

步驟2 相關的標準正態隨機變量轉化為不相關的正態隨機變量.

將相關的標準正態隨機變量Y＊＝（Y＊1Y＊2…Y＊n）T線性變換為不相關的正態隨機變量Y＝（Y1Y2…Yn）T，Yi～N（μi，σi2）.

變換過程如下：

設隨機變量Y＊＝（Y＊1Y＊2…Y＊n）T的協方差矩陣為

由線性代數理論可知，矩陣CY＊ 可通過式（12）線性變換成對角矩陣：

其中A是一個正交矩陣，它的列向量等于矩陣CY＊ 的特征向量，對角矩陣CY由式（13）計算：

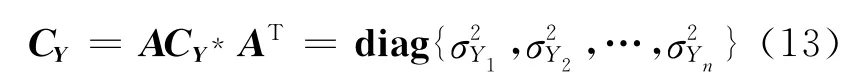
對角矩陣CY的對角元素σ2Yi等于矩陣CY＊ 的第i個特征值.由式（12）可得互不相關的正態隨機變量Y＝（Y1Y2…Yn）T.

步驟3 變量正態分布相關時零件單模可靠度求解.

經過步驟1、步驟2所述方法變換后，可靠度的求解轉化為1.1中討論的問題，按照1.1中提供的方法就可以得到考慮隨機變量正態分布且相關時的零件單模失效下的可靠度.

1.3 含有非正態隨機變量且相關時零件單模可靠度求解理論

研究發現，自然界中大多數的物理量在經過無數次的統計分析后都近似服從正態分布，因此有關正態分布函數的性質、特征、數字特征等研究也最多，發展了許多可用的結論及大量的可供參考查閱的數據.基于此現行對于由高維極限狀態函數表示的可靠度關系式的求解都是以各隨機變量服從正態分布為前提下得出的.然而面對多維極限狀態函數中含有非正態隨機變量的情形，只有將非正態隨機變量轉化為正態隨機變量，才能利用現有成熟的、計算精度高的可靠度理論進行機械零件可靠度的求解，本節將對隨機變量中含有非正態隨機變量的情形進行研究.

假設機械零件單模失效的極限狀態方程為

其中X＝（X1X2…Xn）T，為影響應力、強度分布的隨機變量，X中含有非正態隨機變量且各隨機變量之間具有相關性.此種情況下機械零件單模失效可靠度求解步驟如下：

步驟1 將X中的非正態隨機變量轉化為正態隨機變量.

（1）Rosenblatt變換（Rosenblatt transformation，RT）［14］

Rosenblatt證明：任意非正態隨機變量X，理論上都可以通過Rosenblatt變換轉化為線性無關的標準正態隨機變量Z.但這種變換具有局限性，需要知道n維隨機變量X的聯合累積分布函數，具體變換形式如下：

設n維隨機變量X的聯合累積分布函數為FX（X），則n維標準正態線性無關隨機變量Z可以通過式（15）得到：

按順序反求式（15）中的方程，可以得到n維標準正態線性無關隨機變量Z：

式（16）中的條件概率密度函數通過聯合概率密度函數按式（17）、（18）求得：

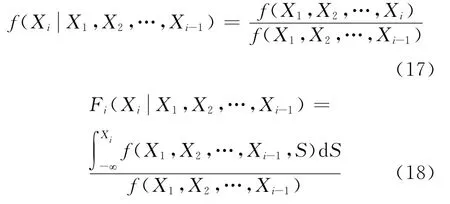
同理可通過逆變換按順序反求式（16）得到X＝（X1X2…Xn）T.由式（16）變換求得不相關標準正態隨機變量Z＝（Z1Z2…Zn）T.

（2）R－F變換［15］

設Xi為臨界破壞面上的特定點，通過令原始分布FXi（Xi）和當量正態分布在特定點Xi處具有相等的概率密度函數和累積分布函數，則可求得當量正態分布的均值和標準差

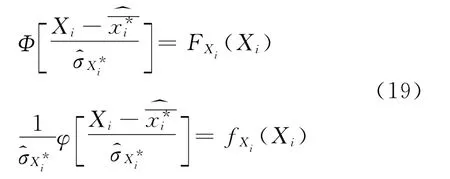
由式（19）得

變換得到正態隨機變量X＊＝ （X＊1X＊2…X＊n）T.

步驟2 含有非正態隨機變量且相關時零件單模可靠度求解.

利用Rosenblatt變換方法進行非正態隨機變量的正態化時，必須利用隨機變量的聯合概率密度函數，這一點在實際中較難實現；但經過此種變換后，含有非正態隨機變量且相關的隨機變量經轉換后直接轉化為不相關的標準正態隨機變量，此時利用1.1中所述的方法就可以快速地求出其可靠度.

R－F變換方法簡單，較容易在計算機上實現，并不需要聯合概率密度函數.將非正態隨機變量正則化為標準正態隨機變量Y＊＝ （Y＊1Y＊2…Y＊n）T；然后按照1.2中所述方法將相關正則化正態隨機變量Y＊＝ （Y＊1Y＊2…Y＊n）T線性變換為不相關正態隨機變量Y＝ （Y1Y2…Yn）T；最后按照1.1中所述方法求解得到考慮隨機變量為非正態分布且相關時機械零件單模可靠度值.

2 機械零件單模失效可靠度求解算法

本章將根據第1章介紹的機械零件單模失效可靠度求解統一模型理論探討可靠度求解的計算機實現算法，機械零件單模極限狀態方程為式（14）描述的n維方程，含有非正態隨機變量，且各隨機變量之間存在相關性.算法中非正態隨機變量利用R－F變換方法正則化為正態隨機變量；可靠度指數β的求解采用H－L 方法，利用Lagrange乘子迭代法導出的公式進行迭代計算.

2.1 Lagrange乘子迭代法推導

Lagrange乘子迭代法詳細敘述如下：

設

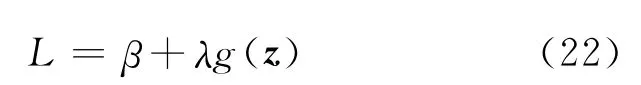
求L的極小值得

令

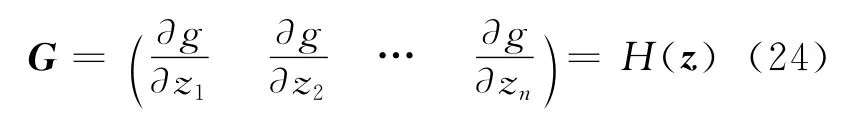
則式（23）可表示為

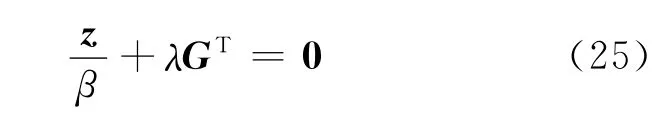
因此

所以

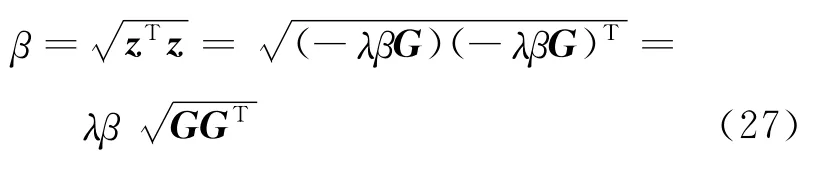
則

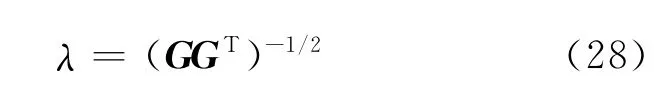
將式（28）代入式（26）得

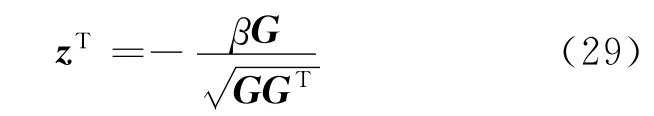
將式（29）代入式（21）得

采用數值方法可以計算出

則式（24）、（29）、（30）即可組成Lagrange乘子迭代法計算的迭代公式.

2.2 機械零件單模可靠度求解算法

假設影響零件單模可靠度的非正態隨機變量為X＝（X1X2…Xn）T，由以上敘述得到可靠度求解算法的完整步驟如下：

步驟1 設置初始點x＝（x1x2…xn）T.

步驟2 在設計點x＝（x1x2…xn）T處利用式（19）、（20）進行R－F 變換，得到，將非正態隨機變量在xi處轉換為正態隨機變量x＊i.

步驟4 對相關的標準正態隨機變量y＊＝（y＊1y＊2…y＊n）T按照式（11）～（13）線性變換為互不相關的正態隨機變量y＝ （y1y2…yn）T.

步驟5 將y＝（y1y2…yn）T由式（2）正則化為互不相關的標準正態隨機變量z＝（z1z2…zn）T，形成臨界破壞面g（z）＝0.

步驟6 在z處計算

步驟7 將zT＝βηα代入g（z）＝0并解得β＝β＋min.

步驟8 采用步驟7計算得到的β重新計算zT＝βηα.

重復步驟6～8直到計算結果收斂（以z穩定作為收斂指標）.

步驟12 由式（5）求得可靠度指數，式（6）求得機械零件單模失效可靠度.

3 算 例

本文以某1.6 MW 風力發電機平行級直齒圓柱齒輪傳動為研究對象，通過對風機齒輪箱傳動系統受力分析得到直齒圓柱齒輪傳動各項參數：齒輪材料及熱處理為17CrNiMo6低碳合金鋼、滲碳淬火，小齒輪轉矩T1＝2.542 8×107N·mm，小齒輪轉速n1＝1 600r／min，齒數Z1＝19，Z2＝94，齒輪模數m＝12mm，齒寬系數φd＝0.4，重合度εa＝1.36，齒輪精度7 級，表面粗糙度Ra＝3.2，使用壽命為20a，高速、輕微振動.本文僅針對齒輪傳動的齒面接觸疲勞可靠性進行分析.

按國家標準規定的方法計算或查線圖得到與齒面接觸疲勞可靠性相關各參量的均值［19］和文獻［20］中給出的方法估算原則得到各參量的均值和標準差如下：Ft＝（81 785.964 9，4 089.298 2）N，d1＝（228，1.14）mm，b＝（91.2，0.456）mm，KV＝（1.323，0.145 5），KHβ＝（1.348 4，0.044 5），KHα＝（1.225 4，0.040 4），ZV＝（0.949 2，0.031 3），KA＝（1.5，0.049 5），σHlim＝（1 450，174）MPa，ZN＝（1，0.033），ZL＝（1，0.033），ZR＝（2.783 6，0.091 9），ZW＝（1，0.005），ZX＝（0.958，0.004 8），ZH＝（2.494 6，0.012 473），ZE＝（189.8，0.949）定義極限狀態方程為

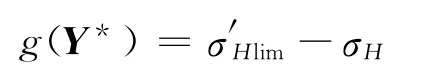
以上各參數的含義及應力σH、強度σ′Hlim的計算式參考國家標準GB 3480—1997.下面分3 種情況對該齒輪傳動的可靠度進行求解.

（1）假設各隨機變量均服從正態分布，其均值和方差如前所述，各隨機變量之間相互獨立，此種情況下根據文獻［21］提供的方法計算得到可靠度指標β＝1.374 112，R＝0.915 330 5.

（2）假設各隨機變量均服從正態分布，相關隨機變量之間的相關性以齒面接觸疲勞應力－強度干涉理論中應力σH與強度σ′Hlim之間的相關性代替，相關系數為ρ.由文獻［21］方法得到該齒輪傳動的齒面接觸疲勞應力S為σH～N（2 887.905 4，205.214 62），齒面接觸疲勞強度δ為σ′Hlim～N（3 670.270 5，531.088 12），則得到可靠度指標

當相關系數ρ在區間［－1，1］內變化，得到可靠度指數β、可靠度R隨ρ變化曲線如圖2所示.

圖2 ρ－β、ρ－R 曲線Fig.2 ρ－β，ρ－Rcurves

由圖2可知，在相關系數ρ從－1 增大到1（即應力、強度相互獨立到應力、強度完全相關）時，可靠度指數β從1.063 1增大到2.400 8，相應的可靠度R從0.856 010增大到0.991 802，可靠度R的相對變化率為15.86%，變化較大.此時若忽略應力、強度之間的相關性將會產生兩種結果：若實際為正相關，此時利用獨立假設理論就會低估系統本身可靠性，通過改變設計來提高其可靠度時設計成本增高，造成不必要的浪費；若實際為負相關，則高估了系統的可靠性，按照此可靠性設計的產品，因過早的失效破壞而達不到設計要求.

以簡單的應力、強度雙變量相關的模型為基礎，分析相關系數對不同零件單模可靠度的影響.以應力、強度相互獨立時可靠度為基準，求解可靠度隨相關系數在［0，1］內的變化曲線，通過對多種具有不同基準可靠度的機械零件ρ－R曲線分析知，基準可靠度越小，考慮與不考慮相關系數時的可靠度差別越大.因此可以得出結論，當在假設變量相互獨立情況下求得的可靠度較大時（如0.999），變量之間的相關性可以忽略，以它們相互獨立求得可靠度，這樣不僅簡化了計算，還不會影響機械零件可靠性優化設計的精度.

（3）假設各隨機變量服從正態分布，通過分析國家標準GB 3480—1997 中各隨機參數的計算知某些隨機變量之間具有相關性：Ft、KV、KHα、KHβ、ZV、b與d1具有相關性；KHβ與b具有相關性.

定義可靠度極限狀態方程中各隨機變量為

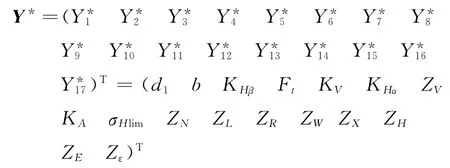
根據各隨機變量計算式設定相關隨機變量相關系數為

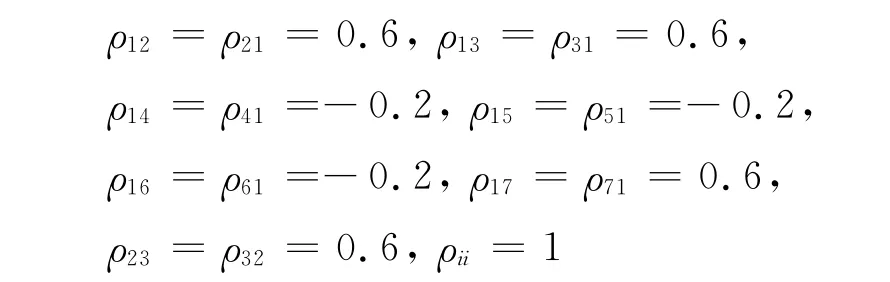
假設相關隨機變量線性變換為非相關變量后的隨機變量為z＝（z1z2…zn）T，利用本文介紹的求解算法求解此種情況下的可靠度，設初始值為z＝（1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1）T，以前后兩次迭代z向量之間的距離作為收斂判據：經過3次迭代后可靠度指數β穩定在4.216 7，并且經過6次迭代后距離L達到7.637 1×10－5.所以求得的可靠度為R＝Φ（4.216 7）＝0.999 987 6.

（4）假設隨機變量Ft、KV、KHα、KHβ、ZV、b、d1服從對數正態分布，7個變量間的相關性情況與（3）中所述相同；其他隨機變量服從正態分布；所有隨機變量的均值和標準差同上.利用本文介紹的求解算法，求解此種情況下的可靠度.外層經5次循環，內層循環分別為63、65、67、68、69次時，可靠度指數β穩定在4.202 1，此時精度為1×10－6.所以求得的可靠度為R＝Φ（4.202 1）＝0.999 987 2.

由以上討論可知，本文介紹的變量相關的機械零件單模可靠度求解算法是可行的，且具有較高的收斂速度，對于復雜的變量相關的可靠度的求解具有重要的應用價值.另外，從考慮各個變量之間的相關性與將只考慮廣義應力、強度之間單相關性求得的可靠度可以看出，差別很大，因此在求解變量相關可靠度時，為使求得的可靠度比較精確，應盡量將各個相關變量的相關性做單獨處理，不要將其等效為應力、強度之間的相關性.

4 結 論

（1）本文以系統中機械零件的單模失效為研究對象，通過探討影響單模失效極限狀態方程的隨機變量的不同特征：是否含有非正態隨機變量、隨機變量間是否相關，建立了考慮含有非正態隨機變量和隨機變量具有相關性時的機械零件單模失效下可靠度求解的統一模型，并對統一模型求解的理論進行了詳細的論述.

（2）基于所建立的機械零件單模失效下的可靠度求解統一模型，提出了高效的計算機求解算法.

（3）通過算例說明了隨機變量之間的相關性對零件單模失效可靠度的影響，表明在零件單模失效求解中忽略隨機變量的相關性將會帶來較大的誤差.通過分析得到，當基準可靠度較大時（如0.999 9），變量之間的相關性可以忽略，這樣在不影響優化設計精度的前提下簡化了可靠度的計算.

（4）本文提出的理論為含有非正態隨機變量時零件單模失效下可靠度的求解提供了一個很好的方法.實例證明，所提出的計算機實現算法收斂速度快，具有很強的實用性.

本文所建立的機械零件單模失效下可靠度求解模型可應用于機械零件任意一種失效模式下的可靠度求解，如熱疲勞、磨損、溫度失效等，這對機械零件考慮多模失效下可靠度理論的發展也具有指導作用.

［1］ Cornell C A.Bounds on the reliability of structural systems［J］.Journal of Structural Division，1967，93（1）：171－200.

［2］ Ditlevsen O.Narrow reliability bounds for structural systems ［J］.Journal of Structural Mechanics，1979，7（4）：453－472.

［3］ FENG Yuan－sheng.A method for computing structural system reliability with high accuracy［J］.Computers ＆Structures，1989，33（1）：1－5.

［4］ 董 聰.現代結構系統可靠性理論［D］.西安：西北工業大學，1993.DONG Cong.The reliability theory of modern structural system ［D］.Xi′an：Northwestern Polytechnical University，1993.（in Chinese）

［5］ 孫玉秋，張祖明.機械系統可靠度計算方法——階段連續界限理論［J］.機械設計與制造，2001（2）：3－5.SUN Yu－qiu，ZHANG Zu－ming.Reliability calculation method of the mechanical system—phases sequence bounds theory ［J］.Machinery Design ＆ Manufacture，2001（2）：3－5.（in Chinese）

［6］ 喻天翔，孫玉秋，張祖明.多模式失效的機械零件可靠度計算新理論［J］.機械工程學報，2003，39（3）：134－138.YU Tian－xiang，SUN Yu－qiu，ZHANG Zu－ming.Reliability computing new theory of mechanical elements with multi failure mode ［J］.Chinese Journal of Mechanical Engineering，2003，39（3）：134－138.（in Chinese）

［7］ 王 正，謝里陽，李 兵.多種失效模式下的機械零件動態可靠性模型［J］.中國機械工程，2007，18（18）：2143－2146.WANG Zheng，XIE Li－yang，LI Bing.Timedependent reliability model of component with multiple failure modes ［J］.China Mechanical Engineering，2007，18 （18）：2143－2146.（in Chinese）

［8］ 王 正，謝里陽，李 兵.考慮載荷作用次數的失效相關系統可靠性模型［J］.東北大學學報：自然科學版，2007，28（5）：704－707.WANG Zheng，XIE Li－yang，LI Bing.Reliability model of failure－dependent system with frequency of loading taken into account ［J］.Journal of Northeastern University：Natural Science，2007，28（5）：704－707.（in Chinese）

［9］ Neves R A，Mohamed－Chateauneuf A，Venturini W S.Component and system reliability analysis of nonlinear reinforced concrete grids with multiple failure modes［J］.Structural Safety，2008，30（3）：183－199.

［10］ 閆 明，張義民，李 鶴，等.機械零件相關失效可靠度計算的二重積分模型［J］.東北大學學報：自然科學版，2011，32（10）：1460－1463.YAN Ming，ZHANG Yi－min，LI He，etal.Double integration model for reliability computation of mechanical components at dependent failure modes［J］.Journal of Northeastern University：Natural Science，2011，32（10）：1460－1463.（in Chinese）

［11］ 吳 波.軸的多失效模型與可靠性研究［J］.機械設計，1998，15（6）：47－48，57.WU Bo.Study on the multi－failure mode model and reliability of the shaft ［J］.Journal of Machine Design，1998，15（6）：47－48，57.（in Chinese）

［12］ 何水清，王 善.結構可靠性分析與設計［M］.北京：國防工業出版社，1993.HE Shui－qing，WANG Shan.Structure Reliability Analysis and Design［M］.Beijing：National Defense Industry Press，1993.（in Chinese）

［13］ 喻天翔，成剛虎，張選生，等.考慮變量相關的機械零件可靠度計算［J］.西安理工大學學報，2003，19（1）：73－75.YU Tian－xiang，CHENG Gang－hu，ZHANG Xuansheng，etal.Reliability computation of mechanical parts in considering variable correlations ［J］.Journal of Xi′an University of Technology，2003，19（1）：73－75.（in Chinese）

［14］ Rosenblatt M.Remarks on a multivariate transformation ［J］.Annals of Mathematical Statistics，1952，23（3）：470－472.

［15］ Rackwitz R，Fiessler B.Structural reliability under combined random load sequences ［J］.Computers and Structures，1978，9（5）：489－494.

［16］ Cramér H.Mathematical Methods of Statictics［M］.New Jersey：Princeton University Press，1999.

［17］ Cornell C A.Structural safety specifications based on second－moment reliability analysis［J］.IABSE Reports of the Working Commissions，1969，4：235－245.

［18］ Hasofer A M，Lind N C.Exact and invariant second－moment code format ［J］.Journal of Engineering Mechanical Division，ASCE，1974，100（EM1）：111－121.

［19］ 《現代機械傳動手冊》編輯委員會.現代機械傳動手冊［M］.2版.北京：機械工業出版社，2002.Editing Committee of Modern Handbook of Mechanical Transmission.Modern Handbook of Mechanical Transmission ［M］.2nd ed.Beijing：China Machine Press，2002.（in Chinese）

［20］ 張義民.汽車零部件可靠性設計［M］.北京：北京理工大學出版社，2000.ZHANG Yi－min.Reliability Design of the Auto Components ［M］.Beijing：Beijing Institute of Technology Press，2000.（in Chinese）

［21］ 芮延年，傅戈雁.現代可靠性設計［M］.北京：國防工業出版社，2007.RUI Yan－nian，FU Ge－yan.Modern Reliability Design ［M］.Beijing：National Defense Industry Press，2007.（in Chinese）