激光修銳砂輪工藝參量的預測和優化算法

周 聰，張 玲，陳根余，2，鄧 輝，蔡 頌

(1.湖南大學激光研究所，湖南大學410082;2.湖南大學汽車車身先進設計制造國家重點實驗室，長沙410082)

引 言

近年來，國內外學者在激光修銳砂輪方面展開了大量的研究，主要采取有兩種方法:一是通過使用不同的激光器和不同的工藝參量進行大量的修銳試驗［1-3］，分析激光修銳后砂輪表面形貌和其磨削性能，積累經驗。此方法成本高、消耗大、見效慢。二是通過理論分析，建立相關的數學模型指導試驗［4-7］。由于激光修銳砂輪是一個復雜的加工過程，建立準確的數學模型難度大、投入多，因此，需要找尋一種結合試驗與仿真的方法，快速找到良好的工藝參量組合。本文中基于神經網絡和粒子群算法研究激光修銳砂輪工藝參量優化模型，使該模型能在一定程度上實現工藝參量預測與優化，這對建立激光修銳砂輪的專家數據庫系統，實現自動化激光修銳砂輪具有重大的現實意義。

目前在工程中應用較為廣泛的預測方法包括:規則推理、案例推理、遺傳算法、人工神經網絡等，這些推理方法有各自的優缺點和適用領域。由于激光修銳砂輪領域研究還不是十分深入，可以用來進行規制推理、實例推理或遺傳算法的專家數據較少，因此，基于人工神經網絡方法建立推理模型比較適合于激光修銳砂輪。這主要有以下幾個原因:(1)人工神經網絡模型很適合于研究非線性關系領域，激光修銳砂輪過程中工藝參量與修銳質量的關系是典型的非線性;(2)人工神經網絡的數據獲取可以來自于數據庫或現場實驗，較為容易實現;(3)建立激光修銳工藝參量與修銳質量關系的神經網絡模型，有助于后續實現基于粒子群算法的工藝參量優化。其具體優化原理是:在用戶提交砂輪型號和所期望的修銳質量時，粒子群算法啟動尋優功能，通過不斷變化粒子的位置和速度并輸入至神經網絡的輸入層，比較網絡的輸出值和期望值，當已實現設定的精度要求或已達到最大的迭代次數時，優化過程結束。

1 激光修銳工藝參量神經網絡模型的研究

1．1 神經網絡模型原理

反向傳播(back propagation，BP)神經網絡(neural network，NN)，即誤差反向傳播算法的學習過程，由信息的正向傳播和誤差的反向傳播兩個過程組成［8］。與傳統的統計學建模相比，BP神經網絡的預測性能更加優越。由于BP神經網絡不需要反應具體的數學模型，并且具有強大的非線性表達能力以及能夠進行復雜邏輯操作等優點，因此，可利用神經網絡模型建立激光修銳工藝參量與工件表面粗糙度之間映射關系來評價砂輪的修銳質量。該模型結合數據庫的原理如圖1所示。由試驗或經驗獲取的工藝參量數據存儲在神經網絡樣本數據庫中，從中調取工藝參量組合建立神經網絡的模型，再根據網絡輸出值和樣本值進行比較，不斷調整神經網絡中的權值V和W，以達到訓練神經網絡模型的目的。

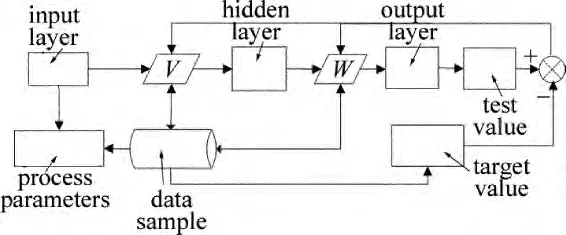
Fig.1 Diagram of laser dressing neural network model combined with database

1．2 激光修銳工藝參量神經網絡模型的建立

1.2.1 BP神經網絡參量的設計 首先是輸入層設計。網絡中數據的緩沖寄存主要靠輸入層來完成，輸入層節點數目主要由容易檢測控制的物理量且對輸出影響較大的參量如激光功率、重復頻率、離焦量、“走刀次數”來決定。因此可將輸入層的節點數確定為4個。

然后是隱含層設計。隱含層設計包含兩方面:層數的選取和節點數的確定。在設計BP網絡時，根據HORNIK等學者［9］的研究成果，隱含層采用 Sigmoid轉換函數。隱含層節點數是通過試驗的方法來選取的，試驗發現隱含層節點數是8時，系統精度最高。

最后是輸出層設計。輸出層的設計主要是依據待解決問題的輸出量來決定輸出層節點數。在激光修銳砂輪過程中，評價砂輪修銳質量的標準有很多，但考慮到實際操作方便，本文中選取砂輪修銳后磨削工件表面粗糙度作為網絡輸出層。

1.2.2 BP神經網絡模型構建 基于BP神經網絡建立了激光修銳工藝參量與工件表面粗糙度之間的3層神經網絡預測模型，如圖2所示。選取激光功率P、離焦量Δf、重復頻率f、走刀次數N為神經網絡的輸入值，工件表面粗糙度Ra為網絡輸出值。

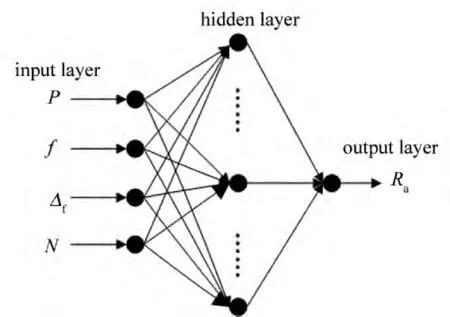
Fig.2 Neural network model of process parameters and surface roughness

基于已建立的神經網絡模型，從樣本數據中選取A組數據作為神經網絡的訓練樣本，而B組數據作為神經網絡的測試樣本，將選取的樣本數據進行歸一化處理。歸一化處理能夠使網絡具有更強的泛化能力，有利于網絡的訓練并加快網絡的收斂。利用訓練樣本對神經網絡進行訓練，輸入層和隱層的傳遞函數分別為tansig和pureline函數，同時用Levenberg-Marquardt算法訓練網絡，當均方誤差達到10-6時，網絡停止訓練。

2 粒子群算法的工藝參量優化的研究

2．1 粒子群算法概述

粒子群算法是基于迭代的優化工具，首先系統初始化一組隨機解，然后通過迭代方式搜尋最優值，最后通過計算評價解的質量。整個搜索更新的過程即跟蹤當前最優解(最優粒子)的過程，它是通過跟蹤當前搜索到的最優解來尋找全局最優。因此，與遺傳算法比較，粒子群算法更為簡單并易操作實現，適合工程領域和科學研究的應用［10-11］。

粒子群算法的鄰域函數在每一個迭代周期根據個體自身位置向量、速度向量、個體歷史信息、群體信息和擾動來產生新的位置狀態。標準的粒子群算法中第i個粒子在k+1時刻的第d維鄰域函數計算公式如下:

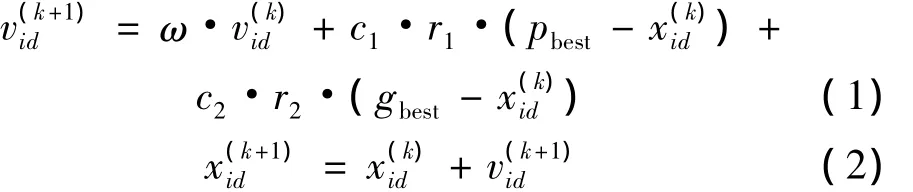
式中，d=1，2，…，D;k是迭代次數;ω稱為慣性因子，ω起著權衡局部最優能力和全局最優能力的作用，ω線性遞減使算法在搜索初期擁有較大的搜索能力，在后期又能夠得到較精確的結果，因此本文中ω的取值隨著算法進行0．9到0．4線性衰減;c1和 c2為學習因子，也稱為加速因子，通常c1=c2=2;r1和r2是［0，1］之間的隨機數，用來保持群里的多樣性;pbest是粒子個體位置最優值，gbest是群體位置最優值。

2．2 數學模型的描述

通過第1.2節中的分析可知，考慮激光功率P、離焦量Δf、重復頻率f、走刀次數N作為網絡的輸入量，則輸入向量矩陣可表示為:X=［x1x2x3x4］T。由于輸出層只有磨削試件表面粗糙度一個節點，因此網絡輸出向量可表示為:

通過BP神經網絡建立兩者之間的關系后，那么輸出向量則可以用輸入向量來表示，模型的數學表達式可以表述為:

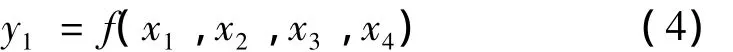
式中，x1，x2，x3，x4分別代表激光功率、離焦量、重復頻率以及走刀次數的上下范圍，y1即代表模型輸出的磨削試件表面粗糙度。

在激光修銳過程的工藝參量優化過程中，對于給定的加工條件，即在加工目標確定的條件下，在約束條件內求解出一組合適的工藝參量，并且使用這組工藝參量使磨削工件表面粗糙度與設定的目標值盡可能接近，即二者相對誤差盡可能小，本質就是求解函數的最小值。

由于采集的數據樣本有限，因此并不是完全準確的整個樣本空間，通過已得到的神經網絡預測模型僅能反映出網絡在限定的樣本空間所建立的模型，并非能十分準確地描述其它樣本空間的工藝參量與磨削工件表面粗糙度值之間的數學模型，所以應該在約束的樣本空間之內進行尋優計算，否則優化的結果就可能不可靠。從試驗過程的工藝參量表可以確定各工藝參量的范圍，0W≤P≤48W，0mm≤Δf≤2.0mm，50kHz≤f≤200kHz，0≤N≤50，那么優化問題的數學表達式可以表示為:

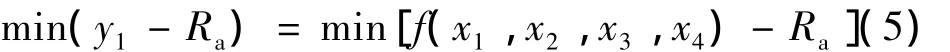
式中，Ra為設定的磨削試件表面粗糙度期望值。

2．3 適應度函數的建立

適應度函數是評價優化結果好壞的依據，因為在優化過程中，粒子的每次迭代是依據適應度函數來進行的。基于已分析可知，本文中所需找尋的是模型的最小值，網絡計算值用y1，期望輸出的磨削試件表面粗糙度為Ra，則適應度函數可構造為:

根據建立的適應度函數，優化問題的數學模型可表示為:

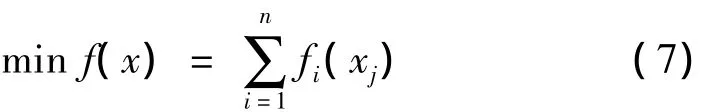
式中，xj表示第j個粒子，變量約束條件為a≤xj≤b，a和b為變量范圍。

2．4 基于神經網絡與粒子群算法的工藝參量優化的實現

采用粒子群算法對激光修銳砂輪工藝參量進行優化的流程如圖3所示。

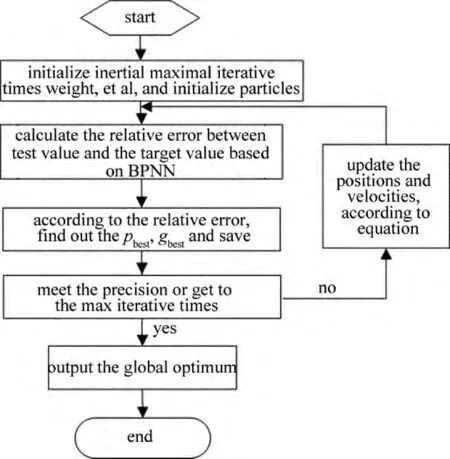
Fig.3 Flow chart for particle swarm optimization algorithm

具體步驟如下。

步驟1:初始化粒子的慣性因子參量、種群規模、加速常數、粒子飛行速度以及最大迭代次數等。初始化粒子群時，為了使粒子更快搜索，與實際值更加接近，可以先從激光工藝參量庫中調取較好參量作為初始值。

步驟2:調用已建立的激光修銳工藝參量與工件表面粗糙度之間的神經網絡模型，計算各粒子的網絡輸出值，比較其與期望值的相對誤差，并把粒子作為每組粒子的個體位置最優值，從這些極值中找出種群的位置最優值，保存當前的最優值。

步驟3:根據(1)式、(2)式更新粒子群的位置和速度，產生新的粒子群，通過計算比較相對誤差獲得新的個體位置最優值pbest和種群位置最優值gbest，將其與已保存的最優值相比較。假如第i個粒子計算得到的相對誤差比原來的小，則保存粒子的新位置，否則仍保留原來的值;假如所有粒子的新位置都比種群的最優值好，則用新的最優值代替原來的種群的最優值。

步驟4:判斷相對誤差是否到達設定的精度或已達到最大迭代次數，若滿足條件則停止計算，此時的粒子位置為優化得到的解，并輸出全局最優值。否則，返回第3步重新計算。

3 優化模型的使用驗證

采集樣本數據的試驗平臺描述如下:激光器由德國IPG公司生產的YLP型脈沖摻鐿光纖激光器。輸出脈沖寬度為210ns，重復頻率為50kHz～150kHz，輸出功率為0W～48W。激光經過焦距為180mm的凸透鏡聚焦后作用于砂輪表面，其焦斑直徑為38μm。激光頭集成了直徑1mm的同軸和側向側吹圓口噴嘴，通過激光夾持器安裝定位在2維電動平臺上，通過2維電動平臺可實現激光頭的精確對焦和軸向進給，其重復定位精度小于0.005mm，分辨率為1.25μm。試驗中采用HZ-74型號的精密臥軸矩臺平面磨床，其主軸最高轉速為2850r/min。試驗平臺示意圖4所示。經激光修銳后的砂輪磨削硬質合金試件，采用由上海泰明光學儀器有限公司生產的高精度激光位移傳感器測量工件表面粗糙度，其型號為JB-4C。

Fig.4 Laser dressing setup

基于采集樣本數據的試驗平臺，開展激光修銳青銅金剛石砂輪試驗。砂輪型號為1A1 100×10×31.75×5 MBD 120 M 100，將修銳后的砂輪磨削硬質合金試件，其牌號為YT5、尺寸規格為50mm×20mm×18mm。磨削試驗過程中工作臺進給速率為80mm/s，砂輪轉速為2000r/min，線速率約為10.5m/s，切削深度為10μm。砂輪修銳后磨削硬質合金，采用高精度激光位移傳感器測量其表面粗糙度。選取25組較成功的試驗數據樣本建立神經網絡預測模型，其中20組數據作為預測模型的訓練集，剩下5組為測試集，當網絡訓練完成后，將5組測試集對網絡進行仿真測試。結果表明:樣本值與仿真值的相對誤差在3%以內，因此神經網絡建立完成。在已訓練好的預測模型上，采用粒子群算法進行工藝參量尋優計算，以5組硬質合金試件的表面粗糙度值為期望值，采用在設定適應度函數值為0.01的的情況下尋優得到的工藝參量值開展激光修銳砂輪試驗，而后多次測量每組青銅金剛石砂輪磨削的硬質合金試件表面粗糙度求平均值。結果如表1所示。

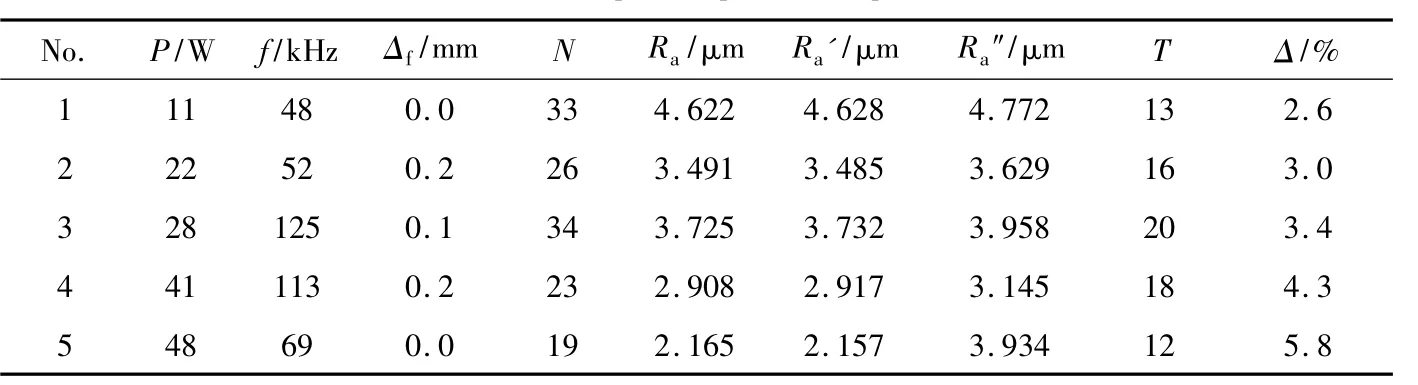
Table 1 Verification of process parameter optimization results

表1中，Ra為表面粗糙度期望值，Ra′為仿真輸出值(即前文中的y1)，Ra″為試驗測量值，T為優化過程中粒子群的迭代次數，Δ為Ra″與Ra的相對誤差。從表中可以看出:粒子群的迭代次數比較少，體現出了粒子群算法搜索能力強的特點;當設定的適應度值為0.01時，優化模型輸出仿真值Ra′與期望值Ra的最大差值為0.009，說明此模型具有較強的優化能力;試驗值Ra″與期望值Ra的相對誤差保持在6%以內，說明優化模型具有一定的指導價值。同時分析優化模型誤差產生的幾大原因:(1)由于選擇的算法并沒有根據本模型特點進行改進，所以建立的優化模型存在著局限性;(2)本優化算法是基于建立的神經網絡模型而開展的，而網絡預測模型本身存在著誤差，因此利用粒子群算法尋優時，會產生誤差積累;(3)在采集數據樣本過程中，由于人為操作測量儀器也會造就數據誤差，這必然影響到所建模型的準確性;(4)影響激光修銳砂輪的工藝參量有許多，而建立模型時只考慮了幾個主要的工藝參量。

4 小結

利用神經網絡建立了激光修銳砂輪工藝參量與工件表面粗糙度之間的神經網絡模型，將5組測試集對網絡進行仿真測試。結果表明，5組測試集的樣本值與輸出值之間的誤差控制在3%以內，這說明該模型具有良好的預測功能。基于預測模型，采用粒子群算法在適應度值為0.01時進行5組工藝參量尋優，利用優化得到工藝參量進行激光修銳試驗。發現試驗值與期望值的相對誤差小于6%，這說明基于粒子群算法的優化模型輸出的工藝參量有較好的現實指導意義。

［1］ BABU N R，RADHAKRISHNAN V，MURTI Y V G S.Investigation on laser dressing of grinding wheels——Part Ⅰ:preliminary study［J］.Journal of Engineering for Industry，1989，111(3):244-252.

［2］ CHEN G Y，LI Z G，BU C，et al.The experiment studies of dressing of bronze-bonded diamond grinding wheels using a pulsed fiber laser［J］.Laser Technology，2013，37(4):705-711(in Chinese).

［3］ MA H L，CHEN G Y，LIU L，et al.Truing and dressing super-abrasive wheels by acoustic-optic Q-switched YAG pulsed laser［J］.Journal of Hunan University(Natural Science Edition)，2004，31(2):56-59(in Chinese).

［4］ DOLDA C，TRANSCHEL R，RABIEYA B M，et al.A study on laser touch dressing of electroplated diamond wheels using pulsed picosecond laser sources［J］.Manufacturing Technology，2011，60(1):363-366.

［5］ CHRISTIAN W，MOHAMMAD R，MAXIMILIAN W，et al.Dressing and truing of hybrid bonded CBN grinding tools using a short-pulsed fiber laser［J］.Manufacturing Technology，2011，60(1):279-282.

［6］ CHEN G Y.The research on mechanism and technology for laser truing and dressing of bronze-bonded diamond grinding wheels by acoustic-optic Q-switched Nd∶YAG pulsed laser［D］.Changsha:Hunan University，2006:28-34(in Chinese).

［7］ CHEN G Y，CHEN C，BU C，et al.Numerical simulation and experiment for online truing and dressing of bronze-bonded diamond grinding wheels with laser［J］.Laser Technology，2012，36(4):433-437(in Chinese).

［8］ YIN C Q.Methods and applications of artificial intelligence［M］.Wuhan:Huazhong University of Science and Technology Press，2007:224-237(in Chinese).

［9］ HORNIK K，STINCHCOME M，WHITE H.Multilayer feed-forward networks are universal approximators［J］.Neural Networks，1989，2(5):359-366.

［10］ LEI D M，YAN X P.Intelligent multi-objective optimization algorithm and its application［M］.Beijing:Science Press，2009:78-80(in Chinese).

［11］ PAN F.Particle swarm optimizer and multi-object optimization［M］.Beijing:Beijing University of Technology Press，2013:9-14(in Chinese).