一維噪聲子空間算法在DOA應用中局限性的研究*

劉建新

(中國空空導彈研究院 洛陽 471000)

?

一維噪聲子空間算法在DOA應用中局限性的研究*

劉建新

(中國空空導彈研究院 洛陽 471000)

對一種應用于DOA中的“一維噪聲子空間算法”進行了討論,指出了現有關于該算法某些結論的失誤,同時討論了在不同入射角情況下時,該算法的應用局限性。計算表明,雖然一維噪聲子空間算法存在理論和應用上的局限性,但在符合應用條件時仍計算出了較為滿意的DOA的結果,同時大大降低了計算量,所以仍有其實用價值。

相控陣通信天線; 經典MUSIC算法; 一維噪聲子空間算法

Class Number TN82

1 引言

在軍用無線通信領域,由于相控陣天線具有傳統天線難以比擬的優勢,因而越來越被人們重視。相控陣通信天線很多能力的實現需要依靠對當前來波方向的自主估計,因此,來波方向估計(Direction of Arrival,DOA)的算法被研究者們所關注。

MUSIC算法是DOA估計中的經典算法之一。MUSIC算法在運算時采用循環迭代的形式,依次估計到達角矩陣的參數直至收斂。在這類循環迭代中,對于各種估計都需要通過多維搜索獲得,這種運算的計算量本就很龐大,而且隨著陣元數增加,計算量會呈指數增長。因而,對算法的簡化是有意義的。

近年來,一種旨在簡化經典MUSIC算法的“一維噪聲子空間算法”被提出,但是現有的諸多文獻在此方面的分析還不夠準確,但這種思想可以為改進DOA算法提供一些啟示和改進途徑。

2 一維噪聲子空間的算法推導

在眾多的信號DOA估計算法中,基于接收信號相關矩陣特征分解的MUSIC算法,具有良好的DOA估計性能,其估計方差接近Cramer-Rao下界[6～7]。但是,在實際應用中,由于快采樣拍數有限,其所接收到的含有噪聲信號,總是與理想信號有一些差值,快拍數越少、信噪比越小,這種差值可能越顯著。這樣的結果就是,在實際運算中出現了被稱作“特征值泄露”的問題。通過計算機仿真計算也可以看到,當信噪比較低和快拍數有限時,陣列相關矩陣的特征分解結果,并不像MUSIC算法理論上所期待的那樣,噪聲子空間中M-D個小特征值相等且等于噪聲方差,而是變成了一系列大小不一的分布。這樣,就很難根據小特征值的重數來確定噪聲子空間的維數,也無法根據小特征值所對應的特征向量構造準確的噪聲子空間,這使算法對到達角的估計性能嚴重下降。為了克服這個問題,一種經過修正MUSIC算法被提出。

在理想情況下,接收信號協方差矩陣的每個噪聲特征向量都分別正交于陣列的每個信號向量和信號子空間,即當陣列流型a(θi)與任意一個噪聲特征向量正交時,所對應的θi即為入射信號的來波方向估計值。也就是說,MUSIC算法是陣列流型a(θi)應與任意一個噪聲特征向量相正交,即:

‖aH(θ)UN‖2=0

(1)

此時,接收信號矩陣的特征值可以排列為

λ1>λ2>…>λD=λD+1=…=λM=σ2

(2)

文獻[5,8]中認為,在實際計算時,由于信噪比較低和快拍數有限、記錄的接收信號不準確等原因,對相關矩陣的特征分解已不能理想地反映應有的正交情況,原有的噪聲特征向量已不再最小、相等且等于噪聲方差,而是變成:

λ1>λ2>…>λD>λD+1>…>λM=σ2

(3)

也就是發生了所謂“特征值泄露”現象。此時,顯然已經沒法根據小特征值的重數來判斷入射信號個數,更無法利用原有的正交特性來估計到達角,進而,就沒法據此估計來波方向了。文獻[5]等認為,各個特征值中,只有最小的特征值及其特征向量,最接近真實值,那么可以假設,此時只有最小特征值是實際噪聲特征值。在這種情形下,原有的由噪聲特征值所對應的特征向量所張成的M-D維噪聲子空間,就由最小特征值對應的特征向量構成的一維空間所代替了。那么,原有的正交關系,變成這樣了這樣:

‖aH(θ|φ)uM‖2=0

(4)

其中uM是最小特征值λM所對應的特征向量。

此時,經典MUSIC算法中的對到達角的估計偽譜:

(5)

就將被修正為

(6)

從上面的偽譜可以看出,由于原有的搜索是在由M-D個特征向量所構成的區間上進行計算,而一維噪聲子空間法相當于只在一個向量上進行運算,所以這種改進型DOA方法被稱作一維噪聲子空間方法。文獻[5,8]等認為,這種方法不僅在一定程度上克服了由于信噪比和采樣數限制而產生的“特征值泄露”問題,在計算量上也有了很大改善。

但是,經過反復驗證,上述結論并不準確。

3 對一維噪聲子空間算法理論局限性的討論

首先,由“特征值泄露”而導致的噪聲特征值分化,并不像文獻[5,8]以及其他文獻中所提到的那樣——只有最小特征值仍接近真實值,全部噪聲特征值從大到小排列變為式(6)的形式。大量的計算表明,分化后的M-D個噪聲特征值實際上是圍繞σ2兩側分布,并且,分化后的噪聲特征值的均值接近σ2。也就是說,在遞減排列的噪聲特征值中,最接近理論值的,并不是最小的噪聲特征值,而是居于多個隊列中間位置附近的某個特征值;并且,最接近理論特征值的實際值,可能大于也可能小于理論值。這樣,就不能簡單的僅以最小特征值來判定理論計算值,而需另外的數學手段來確定了,比如,可以先計算小特征值的均值,再尋找最接近此均值的特征值。

其次,在M-D個小特征值中,與其他特征矢量相比,最接近理論值σ2的噪聲特征值所對應的特征向量,與當前方向下的陣列流型矢量的正交性并不一定是最好的。一系列計算表明,與陣列流型矢量有著最佳正交性的特征矢量所對應的特征值,在固定的排序中呈現某種隨機分布。

從上面的分析可以看到,實際上對一維噪聲子空間進行推導的前提并不正確。但是,作為一種富有啟發性的思路,仍有借鑒性。

再回頭分析一下因受“特征值泄露”影響而不準確的噪聲特征值。前面提到過,此時的噪聲特征值已經不再“相等且等于噪聲的方差”,而是圍繞理論上的特征值上下進行分布。相應的,原有的特征向量也會變得不再與陣列流型矢量嚴格正交。如果按照原有的計算步驟,將噪聲子空間與陣列流型正交運算并搜索極值的話,計算偏差顯然很大。但是可以發現,雖然“特征值泄露”后每個特征向量都產生了一定的偏差,但是任意單個特征向量的正交性都優于“特征值泄露”后的整個噪聲子空間的正交性。也就是說,任選一個特征向量,如最小特征值所對應的特征向量,然后將其替換原有的噪聲子空間,所得的結果就應比替換前要好。從這個角度來看,雖然文獻[5,8]所述的以為噪聲子空間方法的理論基礎并不完全正確,但是其對計算結果確實有一定的改善,同時,也確實大大降低了計算量,所以,對于這種應用于DOA中的一維噪聲子空間思想,仍可以借鑒。

4 對一維噪聲子空間算法應用局限性的討論

事實上,一維噪聲子空間算法除了理論上存在商榷之處外,應用中也有局限性。下面計算采用一維噪聲子空間方法時,一個入射信號和兩個入射信號的MUSIC譜。以8元均勻直線陣為例,設有兩個信號分別從0°和30°方向入射,接收端信噪比為10dB,其MUSIC譜如圖1。

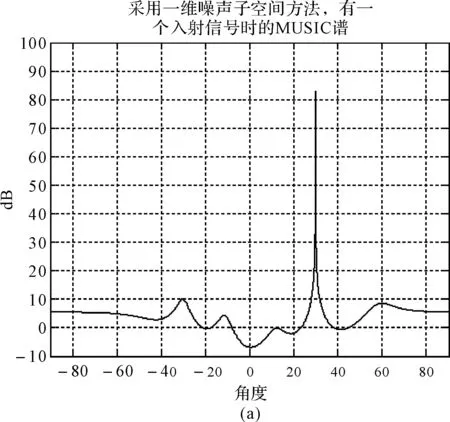
圖1 有一個和兩個信號入射時的MUSIC譜

圖1計算了有一個和兩個入射信號時,采用一維噪聲子空間計算得到的MUSIC譜。圖1(a)可以看出,當有一個入射信號時,可以根據譜峰搜索將來波方向成功的計算出來,所得的偽譜尖銳,且與角度對應比較準確,結果令人滿意;但是圖1(b)中,當有0°和30°兩個入射信號時,雖然在這兩個方向出現了峰值,但是沒有信號的一個方向-33°附近也出現了一個峰值,而且該峰值比0°方向的峰值更高。從這兩個圖的對比可以看到,當入射信號超過一個時,譜峰高度可能會低于沒有入射信號的方向,此時就會使計算發生錯誤。

通過觀察和分析可以知道,雖然一維噪聲子空間能夠減小計算量,同時也可以提高MUSIC的譜峰高度,但是在有多個入射信號或者低信噪比的情況下,非期望的峰值可能會高于期望方向的峰值,從而導致計算失敗,這是一維噪聲子空間方法的應用局限性。

5 結語

論文分析了一種“一維噪聲子空間算法”在DOA估計方面的優點和應用局限性,然后DOA結果進行了計算。計算表明,該種改進型自校準算法在只有一個入射波時仍能有效地估計出來波方向,且計算量有了較大的改善,但入射波在某些情況下時,可能會出現計算錯誤的情況。

[1] Robert J Mailloux.相控陣天線手冊[M].北京:電子工業出版社,2007.

[2] 劉鳴,袁超偉,賈寧,等.相控陣天線技術與應用[M].北京:機械工業出版社,2007.

[3] 蘇衛民,顧紅,倪晉麟.通道失配對MUSIC空間譜及其分辨力的影響[J].電子學報,1998,26(9):142-145.

[4] 王鴻興.天線陣列自校正算法研究[D].長沙:國防科學技術大學,2006.

[5] 羅利春.基于一維噪聲子空間的空間譜估計算法[J].中國空間科學技術,1994(1):1-8.

[6] Haykin S, Reilly J P, Kezys. Some aspects of array[J]. Signal processing, IEEE Proceeds-F,1992,139(1):1-26.

[7] Hill D S. Multiple signal DF using super resolution: a practical assessment. ECEJ, DEC,1990:221-232.

[8] 張浩,張志軍,朱國軍.采樣數據重構的修正一維噪聲子空間算法[J].電聲技術,2006(11):4-6,11.

[9] 李海鵬.基于空間譜估計的陣列誤差校正方法研究[D].西安:西安電子科技大學,2011.

[10] 閔永生,羅景青,吳世龍.基于均勻圓陣的方位估計及互耦自校正算法[J].探測與控制學報,2011,33(6):66-70.

[11] 張志軍,張浩,朱國軍.陣列幅相誤差影響下的一維噪聲子空間算法[J].兵工自動化,2006,25(12):45-47.

Limitations of the Application of One-dimensional Noise Subspace Algorithm in DOA

LIU Jianxin

(China Airborne Missile Academy, Luoyang 471009)

The one dimension noise subspace algorithm are discussed. Some mistakes of that algorithm are pointed out, and limitations of that algorithm are studied under different conditions. Conclusion is that although there are limitations on the theory and application, but under certain conditions results of DOA are satisfied, meanwhile the amount of calculation is greatly reduced, so there is still values for that algorithm.

phased array antenna, classic MUSIC algorithm, one-dimensional noise subspace algorithm

2015年6月8日,

2015年7月29日

總裝“十二五”高技術支撐項目(編號:6190102503)資助。

劉建新,男,碩士,助理工程師,研究方向:彈載制導數據鏈等。

TN82

10.3969/j.issn.1672-9730.2015.12.011