純黏土與砂-黏土混合物滲透特性差異及機理分析

吳子龍 朱向陽 江舜武 劉華山 鄧永鋒

(1 東南大學巖土工程研究所，南京210096)

(2 連云港贛榆港區建設現場指揮部，連云港222100)

(3 江蘇新蘇港投資發展有限公司，連云港222042)

土體的滲透系數是巖土體材料的一個重要參數，因此定量評價土體的滲透特性且提出簡單有效的定量表達式顯得尤為重要.到目前為止，國內外大量學者對其進行了研究，取得了豐碩的成果.Taylor［1］和Mesri 等［2］通過一系列的滲透試驗指出，重塑黏土滲透系數k 的對數值隨孔隙比e 的變化呈線性關系;Mesri 等［2］和Nagaraj 等［3-5］針對含水率為液限附近的飽和重塑黏土，以各級荷載下的孔隙比與液限狀態下的孔隙比之比值(e/eL)作為歸一化指標，建立了其與滲透系數k 之間的線性關系，且提出了一個定量表達式;而Achari 等［6］在Nagaraj 試驗基礎上，提出了40% ～60%液限范圍內重塑黏土滲透系數的預測方法，進一步提高了滲透系數的預測精度.

在地基土體中不可避免地含有一定含量的砂，尤其是以人造吹填土作為地基土時，土體中砂含量很大且分布極其不均勻.針對這種砂-黏土混合物，目前大部分學者重點研究了砂含量(黏土含量)對其液限［7］、滲透特性［8-11］的影響，而關于如何定量評價砂-黏土混合物的滲透特性以及其與純黏土滲透特性之間是否存在差異性，目前尚未見報道.

本文依托連云港贛榆港區吹填工程，在室內配制了一系列的純黏土和砂-黏土混合試樣，在常規固結實驗基礎上反演了其滲透系數;將常用于評價重塑純黏土滲透特性的歸一化指標e/eL拓展運用于砂-黏土混合物中，發現此指標也能夠評價砂-黏土混合物的滲透特性，但是純黏土與砂-黏土混合物歸一化滲透特性之間存在明顯的差異性.本文結合砂-黏土混合物四相模型，從砂孔隙比和黏土孔隙比等角度對此現象進行了詳細的機理分析;最后，基于室內試驗數據提出了一種經驗公式，使其既能預測重塑純黏土的滲透系數，亦能夠預測砂-黏土混合物的滲透系數.

1 試驗

1.1 試驗材料

本次試驗材料由砂和黏土組成.試驗所用砂為標準石英砂，其主要成分為SiO2.黏土由商用膨潤土(Bentonite)和高嶺土(Kaolin)復配而成，膨潤土主要成分為SiO2和Al2O3，而高嶺土主要成分為Al2O3和CaO，同時還有少量的Fe2O3.其基本物理指標如表1所示.

1.2 試驗方案

本次試驗中，黏土是在實驗室配置而成的.首先按照質量控制法，分別稱取一定質量的膨潤土和高嶺土，然后將它們充分攪拌均勻，以此來模擬現場黏土，膨潤土和高嶺土的質量比為7/3 和5/5.當黏土配制完成后，將一定質量的黏土和砂混合在一起使之形成砂-黏土混合物.本次試驗共設定了5 種不同含量Wc(干燥狀態下黏土質量與混合試樣總質量之比)的黏土，分別為30%，40%，50%，60%以及100%.為了消除砂級配對混合物滲透特性的影響，設定所有混合物試樣的砂級配一致，配制的純黏土和砂-黏土混合物的粒徑累積曲線(膨潤土質量mB與高嶺土質量mK之比為7/3)如圖1所示.圖中，S 表示試驗所用標準砂，C 表示復配黏土.具體的試驗方案以及復配土的參數見表2，表中，砂比重Gss與復配黏土比重Gsc均是根據ASTM D854 測試所得，而砂-黏土混合物比重Gs則是按照加權平均值法計算所得.

表1 膨潤土和高嶺土基本物理指標

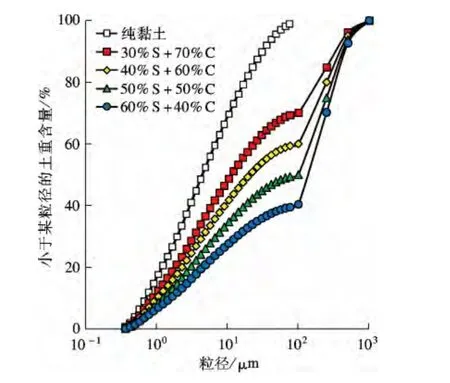
圖1 粒徑累積曲線

表2 試驗方案與復配土參數

1.3 試驗方法

本文中重塑純黏土和砂-黏土混合物的滲透系數是根據常規固結試驗數據反演所得，而在進行固結試驗之前，需先制作固結試樣，其制備方法與文獻［9］相同:首先根據預設的質量配比將黏土和石英砂充分混合均勻，然后加入一定量的蒸餾水，使混合試樣的含水率等于其液限(以此來模擬現場吹填土高含水率情況).配樣完成后，將配置好的混合試樣裝在密封袋中，放置在標準養護室內24 h，養護溫度為(20 ±2)℃，相對濕度為95%.最后將養護后的混合土緩慢填入環刀，為了排除試樣中的氣泡，試樣分3 次填充，且每次填充后，輕微壓實試樣.當試樣制作完成后，按照標準的規范流程將其裝置在標準固結儀上開始進行固結試驗，其試驗加載按加載率(加載增量與前一級荷載的比值)為1 進行，即荷載為12.5，25.0，…，1 600 kPa.

當固結試驗結束后，根據太沙基一維固結理論計算純黏土和砂-黏土混合物試樣的滲透系數，計算式為

式中，Cv為固結系數;mv為體積壓縮系數;γw為水的重度，取9.81 kN/m3.文獻［10，12］對砂-黏土混合物的滲透系數計算亦常采用以上理論方法.

2 試驗結果及機理分析

2.1 滲透特性及歸一化分析

當固結試驗結束后，根據式(1)計算純黏土和砂-黏土混合物的滲透系數k，滲透系數k 與孔隙比e 的關系如圖2所示.

圖2 孔隙比e 與滲透系數k 的關系

圖2表明，在相同的黏土礦物配比和孔隙比下，試樣的滲透系數隨著砂含量的增加而增加;黏土礦物組成也是影響試樣滲透系數的重要因素，隨著膨潤土含量的增加，滲透系數變小.對于這種試驗現象，Mesri 等［2］從黏粒粒徑和滲透通道直徑等方面給出了詳細的解釋說明:蒙脫石粒徑最小而高嶺石粒徑最大，粒徑越小致使滲透通道直徑越小，而滲透系數的大小與滲透通道的直徑成正比［13］.

此外，從圖2也可以看出，砂-黏土混合物滲透系數的對數值與孔隙比之間呈現非線性關系，這與重塑純黏土的滲透特性不一致(重塑純黏土滲透系數的對數值隨孔隙比的變化呈直線關系［1-2］).

為了更加方便地評價混合物的滲透特性，本文將常用于評價重塑純黏土滲透特性的歸一化指標e/eL拓展運用到含水率為液限的混合物中，從而建立e/eL與滲透系數之間的聯系.所有試樣的e/eL與k 的關系如圖3所示，其中eL為液限狀態孔隙比.

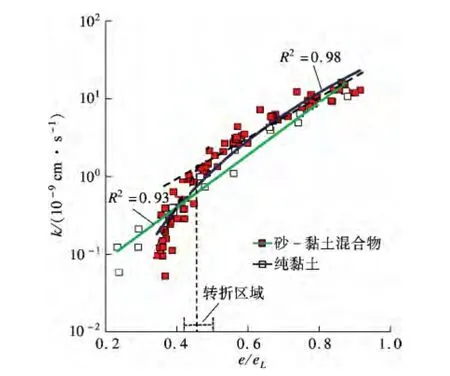
圖3 e/eL 與k 之間的關系

由圖3可見，針對純黏土能夠建立e/eL與k之間的線性關系(擬合系數R2=0.93)，這與Mesri等［2］和Nagaraj 等［3-5］所得到的結論相一致.與此同時，建立了砂-黏土混合試樣e/eL與k 之間特定的擬合經驗關系(擬合系數R2=0.98)，但是它們之間呈現非線性關系，這明顯不同于重塑黏土的線性關系.從圖3中還可以發現，純黏土與砂-黏土混合物2 條擬合線之間存在一個明顯的轉折區域，在轉折區域的右邊，2 條擬合曲線吻合性較好，而在轉折區域的左邊兩者差異性較大.而轉折區域即是砂骨架形成區域，骨架形成之前，混合物表現出黏土性質，使純黏土和砂-黏土混合物的2 條擬合曲線吻合性良好;而在骨架形成后，砂顆粒的接觸抑制了混合物孔隙比的減小［9］，導致兩者之間的差異性，即混合土擬合曲線位于純黏土擬合曲線的右邊.

砂骨架的形成亦可以從試樣固結系數Cv的變化規律(見圖4)得到輔證.從圖4可以看出，砂含量和黏土礦物組成是影響試樣固結系數的內在因素，隨著砂含量的增加或者mB/mK比例的減小，試樣的固結系數變大;荷載是影響固結系數的外在因素，隨著荷載P 的增加，所有試樣的固結系數均增加，但是砂-黏土混合物和純黏土固結系數的變化規律不一致，其轉折區域在400 kPa 左右.當荷載小于400 kPa 時，固結系數的變化規律大致相同，均隨著荷載緩慢增加，因為此時混合土并沒有形成砂骨架，其表現出黏土性狀;而當荷載大于400 kPa 時，混合土在荷載的作用下形成了砂骨架，部分砂顆粒彼此接觸，表現出砂土的性狀，致使混合土的固結系數明顯要大于純黏土的固結系數.

圖4 固結系數Cv 與荷載P 之間的關系

2.2 砂骨架形成機制及機理解釋

通過建立各種參數之間的關系，可發現純黏土和砂-黏土混合物滲透性狀會產生一定的差異性，其本質原因在于混合物在加載后期形成了砂骨架，轉折區域在400 kPa 左右.本文在四相模型(見圖5)以及黏土孔隙比ec計算式［14-16］的基礎上推導出砂孔隙比es的計算公式，并從ec和es等角度對砂骨架的形成機制進行詳細的說明.混合土的四相模型ec以及es的計算公式分別為

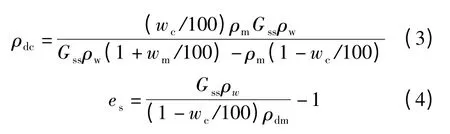
式中，ρw為水的密度;ρm為混合土的密度;ρdm為混合土的干密度;wm為混合土的含水率;wc為混合土中黏土的含量.通過對式(2)～(4)的計算，得到了混合土的es與ec值.它們與荷載的變化關系如圖6和圖7所示.

圖5 砂-黏土混合物四相模型

圖6 砂孔隙比es 與荷載P 之間的變化關系

由圖6可以看出，混合物的es隨著荷載的變化，出現了明顯的轉折點(荷載為400 kPa)，當荷載小于400 kPa 時，es隨著荷載的增加呈直線降低，因為此時的混合物在荷載作用下并沒有形成砂骨架;而當荷載大于400 kPa 時，混合物形成了砂骨架，砂顆粒的彼此接觸抑制了es的減小，致使其變化明顯變緩.由圖7可見，當荷載小于400 kPa時，砂-黏土混合物和純黏土擬合曲線基本一致，而當荷載大于400 kPa 后，混合物擬合曲線位于純黏土擬合曲線的上方，其本質原因亦是砂骨架形成后，由于砂顆粒的彼此接觸，抑制了ec的減小，導致了以上現象的發生.圖7中，ecL為液限狀態(即起始狀態)下的黏土孔隙比.

圖7 ec/ecL與荷載P 之間的關系

2.3 滲透系數的預測公式

由圖3可以看出，針對不同黏土含量和黏土礦物組成的砂-黏土混合物能夠建立e/eL與k 之間的擬合經驗公式，以此公式可以預測混合土的滲透系數，然而該公式卻不能預測純黏土的滲透系數.因此，有必要提出一種新型的經驗公式，使其既能預測混合土，亦能預測純黏土的滲透系數.本文參照Kozeny-Carman 公式，即

式中，SSA 為比表面積，SSA= (2.0 × 105Gs)為水的黏滯系數;CK-C為系數.以所有試樣的e3/(1 + e)為橫坐標，以滲透系數k 為縱坐標，得到其關系如圖8所示.圖8顯示，針對所有純黏土與砂-黏土混合試樣均能夠建立e3/(1 +e)與k 之間的關系，即

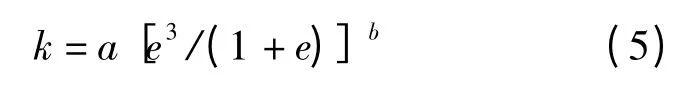
經過數據分析與處理后發現，系數a、指數b與液限之間具有良好的統一性(見圖9).其中，指數b 幾乎不發生改變，接近于2.0，而系數a 能用液限wL表示，即

將b=2 和式(6)代入式(5)，即可建立滲透系數k 與液限wL及e3/(1 +e)之間的表達式，即

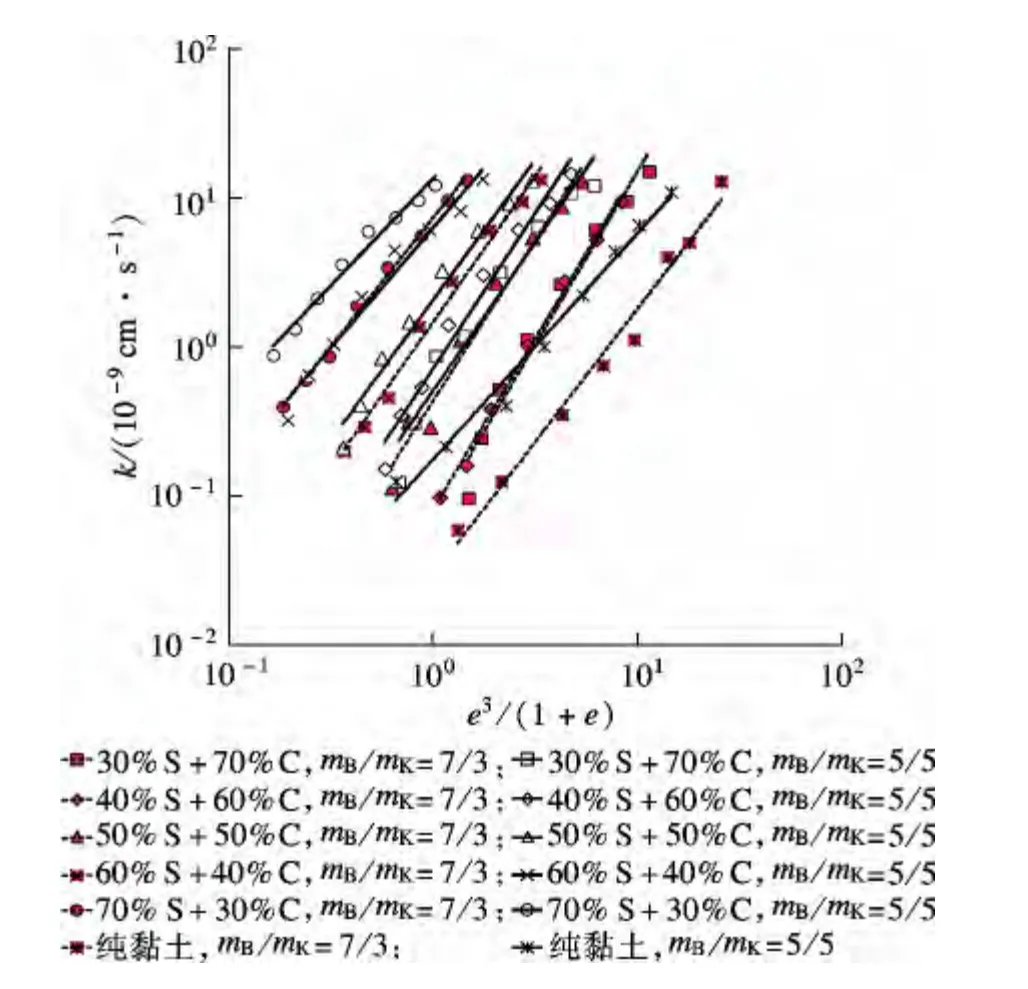
圖8 e3/(1 +e)與k 之間的關系

圖9 表達式參數與液限wL 之間的關系

為了驗證式(7)和式(8)的合理性和有效性，將試驗反演值與公式預測值進行了對比分析，如圖10所示.由圖可以發現，兩者吻合性極好(擬合系數R2=0.95)，這證明了以式(7)和(8)預測純黏土和混合土滲透系數的準確性和可行性.

此外，從式(8)還可以發現，滲透系數k 與液限wL之間呈負相關性，而其與孔隙比e 之間呈正相關性，這與Kozeny-Carman 公式一致，但是其特定系數卻有明顯區別.首先，k 與e3/(1 +e)這一組合為2 次方關系，而在Kozeny-Carman 公式中為1次方;其次，k 與液限wL之間呈－4.94 次冪關系，而Kozeny-Carman 公式中卻為－2.90 次冪關系，這種現象需要在后續的研究中進行深入的探討.

圖10 滲透系數試驗值與經驗公式預測值之間的關系

3 結論

1)常用于評價純黏土滲透特性的歸一化指標e/eL能夠運用于砂-黏土混合物中，以此指標能夠建立其與滲透系數k 之間特定的關系式.

2)純黏土與砂-黏土混合物歸一化滲透特性之間存在明顯的差異性，其本質原因在于混合土在荷載作用下形成了砂骨架;骨架形成之前，表現出似黏土性狀，而在骨架形成之后，砂顆粒彼此接觸，抑制了孔隙比的減小，致使它們的擬合曲線出現明顯差異.對于本次研究而言，當e/eL=0.40 ～0.42或豎向荷載P=400 kPa 左右時，混合土的滲透性狀發生明顯改變.

3)本文提出了一種預測純黏土和混合土滲透系數的經驗公式;同時通過室內試驗數據驗證了以此公式預測滲透系數的可行性和準確性.

References)

［1］ Taylor D W.Fundamentals of soil mechanics［J］.Soil Science，1948，66(2):161.

［2］ Mesri G，Olson R E.Mechanisms controlling the permeability of clays ［J］.Clays and Clay Minerals，1971，19(3):151-158.

［3］ Nagaraj T S，Miura N.Soft clay behavior:analysis and assessment［M］.Rotterdam:A A Balkema，2001.

［4］ Nagaraj T S，Murthy B R S.A critical reappraisal of compression index equations［J］.Géotechnique，1986，36(1):27-32.

［5］ Nagaraj T S，Pandian N S，Raju P S R N.Stress statepermeability relationships for fine-grained soils［J］.Géotechnique，1993，43(2):333-336.

［6］ Achari G，Joshi R C.A reexamination of the permeability index of clays:discussion［J］.Canadian Geotechnical Journal，1994，31(1):140-141.

［7］ Sivapullaiah P V，Sridharan A.Liquid limit of soil mixtures［J］.Geotechnical Testing Journal，1985，8(3):111-116.

［8］ Yeo S S，Shackeiford C D，Evans J C.Consolidation and hydraulic conductivity of nine model soil-bentonite backfills［J］.Journal of Geotechnical and Geoenvironmental Engineering，2005，131(10):1189-1198.

［9］ Fukue M，Okusa S，Nakamura T.Consolidation of sand-clay mixtures［J］.ASTM Special Technical Publication，1986 (892):627-641.

［10］ Sivapullaiah P V，Sridharan A，Stalin V K.Hydraulic conductivity of bentonite-sand mixtures［J］.Canadina Geotechnicd Journal，2000，37(2):406-413.

［11］ Pandian N S，Nagaraj T S，Raju P S R N.Permeability and compressibility behavior of bentonite-sand/soil mixtures［J］.American Society for Testing and Materials，1995，18(1):86-93.

［12］ Watabe Y，Yamada K，Saitoh K.Hydraulic conductivity and compressibility of mixtures of Nagoya clay with sand or bentonite［J］.Géotechnique，2011，61(3):211-219.

［13］ Lamb H.Hydrodynamic［M］.6th ed.London:Cambridge University Press，1932:160-172.

［14］ Lee J O，Cho W J，Chun K S.Swelling pressures of a potential buffer material for high-level waste repository［J］.Journal of the Korean Nuclear Society，1999，31(2):139-150.

［15］ Dixon D A，Gray M N，Thomas A W.A study of the compaction properties of potential clay-sand buffer mixtures for use in nuclear fuel waste disposal［J］.Engineering Geology，1985，21(3):247-255.

［16］ Wang Q，Tang A M，Cui Y J，et al.The effects of technological voids on the hydro-mechanical behavior of compacted bentonite-sand mixtures［J］.Soils and Foundations，2013，53(2):232-245.

［17］ Mbonimpa M，Aubertin M，Chapuis R P，et al.Practical pedotransfer functions for estimating the saturated hydraulic conductivity［J］.Geotechnical and Geological Engineering，2002，20(3):235-259.