附加δ勢(shì)壘對(duì)一維半無(wú)限深勢(shì)阱影響的研究
唐義甲,韓修林
(阜陽(yáng)師范學(xué)院 物理與電子工程學(xué)院,安徽 阜陽(yáng) 236037 )
?
附加δ勢(shì)壘對(duì)一維半無(wú)限深勢(shì)阱影響的研究
唐義甲,韓修林
(阜陽(yáng)師范學(xué)院 物理與電子工程學(xué)院,安徽 阜陽(yáng) 236037 )
摘要:通過(guò)對(duì)添加δ勢(shì)壘的一維半無(wú)限深勢(shì)阱的薛定諤方程進(jìn)行求解,得到了粒子運(yùn)動(dòng)的波函數(shù)和能級(jí)的相關(guān)公式,分析發(fā)現(xiàn),δ勢(shì)壘的添加以及它的強(qiáng)度與位置的變化對(duì)能級(jí)都有影響。對(duì)比不含δ勢(shì)壘的一維半無(wú)限深勢(shì)阱的能級(jí),探究δ勢(shì)壘的添加對(duì)原能級(jí)產(chǎn)生的影響,并利用Mathematica作圖來(lái)直觀顯示這一影響。
關(guān)鍵詞:δ勢(shì)壘;一維無(wú)限深勢(shì)阱;能級(jí)
薛定諤方程大致可以分為兩類(lèi):定態(tài)薛定諤方程和含時(shí)薛定諤方程。定態(tài)薛定諤方程的研究主要利用橢圓偏微方程理論和變分法理論,這方面的結(jié)果非常豐富[1-2]。含時(shí)薛定諤方程在上世紀(jì)70年代以后,隨著調(diào)和分析手段的引入而發(fā)展迅速,尤以著名數(shù)學(xué)家J. Bourgain,T. Tao,C. Kenig和F. Merle等人的工作備受矚目[3-4]。
由于δ函數(shù)的特殊性,δ(x)勢(shì)在原子、分子、固體及多體等問(wèn)題中均有廣泛應(yīng)用[5-6],而在量子力學(xué)定態(tài)薛定諤問(wèn)題中引入δ(x)勢(shì)卻鮮有報(bào)道[7-8]。本文在已有嚴(yán)格解的一維半無(wú)限深方勢(shì)阱內(nèi)引入δ(x)勢(shì), 采用理論分析、數(shù)值計(jì)算與作圖顯示相結(jié)合的方法,對(duì)δ勢(shì)引起的能級(jí)及波函數(shù)進(jìn)行修正。
1附加δ勢(shì)的半無(wú)限深方勢(shì)阱
設(shè)質(zhì)量為m的粒子,作一維運(yùn)動(dòng),在半無(wú)限深方勢(shì)阱中附加δ勢(shì)后,如圖1所示,勢(shì)能為
(1)
其中,μ是描述勢(shì)阱位置的無(wú)量綱參數(shù),取值區(qū)間為(0,1)。
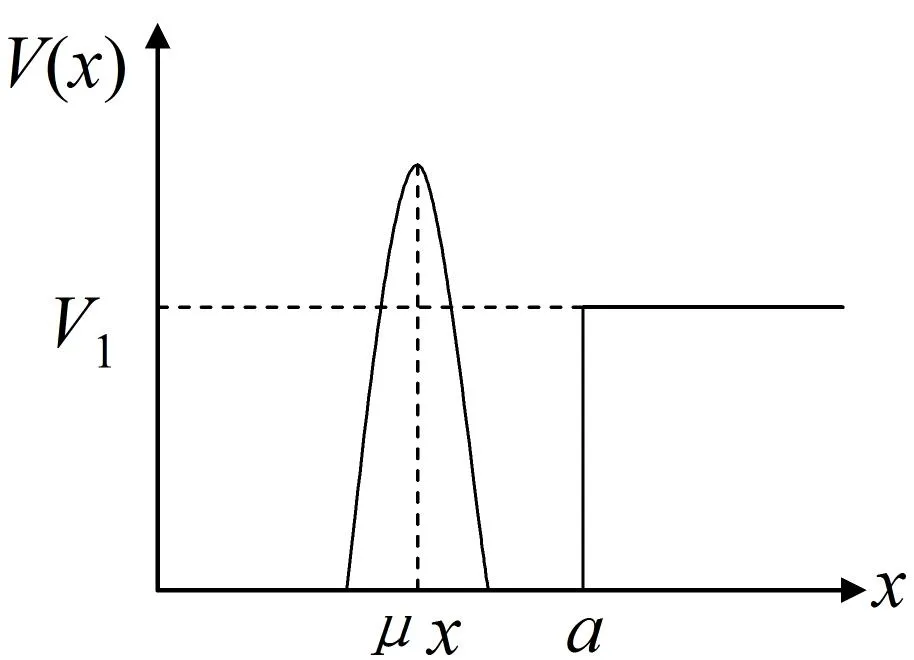
圖1 附加δ勢(shì)壘的一維半無(wú)限深勢(shì)阱
粒子的波函數(shù)與能量滿足定態(tài)薛定諤方程:
(2)
由于勢(shì)能不連續(xù),定態(tài)薛定諤求解可分為四個(gè)區(qū)域:
(3)
由于束縛態(tài)粒子的能量有限性,在區(qū)域Ⅰ內(nèi)波函數(shù)應(yīng)為零,即波函數(shù)ψ0(x)=0。
在區(qū)域Ⅱ,Ⅲ內(nèi),定態(tài)薛定諤方程為
(4)
上式可以簡(jiǎn)化為
(5)
其中,
(6)
在區(qū)域Ⅳ內(nèi),定態(tài)薛定諤方程為
(7)
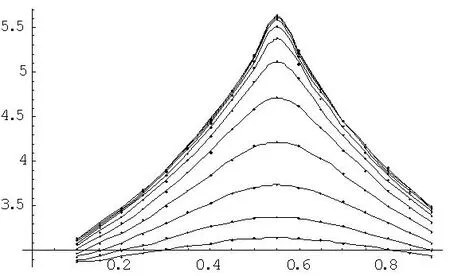
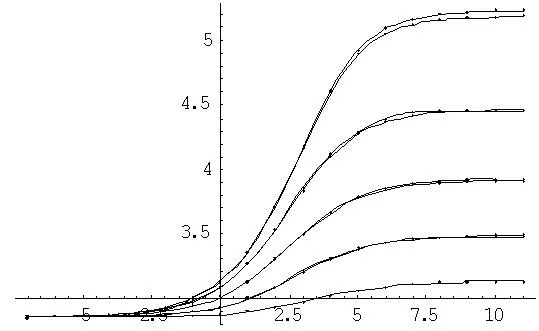
由束縛態(tài)條件知E ψ″-β2ψ=0 (8) 其中 (9) 由波函數(shù)的連續(xù)性,得到在邊界x=0處 ψ1(0)=ψ0(0)=0 (10) x=μa是方程(5)的奇點(diǎn),ψ′(μα)不連續(xù),利用波函數(shù)連續(xù)條件并對(duì)(5)式積分,得 ψ2(μa+0)+ψ1(μa-0)= ψ(μa) (11) 在x=a處,由波函數(shù)一階導(dǎo)數(shù)連續(xù),可得到 (12) 2半無(wú)限深方勢(shì)阱中附加δ勢(shì)的粒子的波函數(shù)與能級(jí) 2.1定態(tài)波函數(shù) 方程(5)的通解為 ψ1(x)=Asin(kx)+A′cos(kx) (14) 考慮到邊界條件(10),可得當(dāng)A′=0,所以區(qū)域II內(nèi) ψ1(x)=Asin(kx) (15) 由方程(8),得到區(qū)域Ⅳ內(nèi)的波函數(shù)為 ψ3(x)=Ce-βx+Deβx (16) 當(dāng)x→∞時(shí),波函數(shù)應(yīng)有限,所以 D=0 (13) ψ3(x)=Ce-βx (17) 方程(5)在區(qū)域Ⅲ內(nèi)的通解為 ψ2(x)=Bsin(kx+φ) (18) 結(jié)合銜接條件(12)得 kcot(kx+φ)=-β (19) 為簡(jiǎn)單起見(jiàn),假定λ=0,則銜接條件(11)變?yōu)?/p> ψ′(μα+0)=ψ′(μα-0) (20) 勢(shì)阱過(guò)渡為半無(wú)限深方勢(shì)阱,如果存在波函數(shù)在μα處為零,則(20)同樣適用于λ≠0,因此假定先波函數(shù)在μα處為零,采用迭代法求解,易解得 (21) A,C可由波函數(shù)連續(xù)性條件和歸一化條件確定,參數(shù)k,β與能量有關(guān),其他參數(shù)可由(19)和(20)式確定。 2.2定態(tài)能量 2017年,聯(lián)盟成員立項(xiàng)或在研創(chuàng)新項(xiàng)目39項(xiàng),形成自主知識(shí)產(chǎn)權(quán)多項(xiàng),包括發(fā)明專(zhuān)利9項(xiàng),實(shí)用新型專(zhuān)利4項(xiàng),軟件著作權(quán)18項(xiàng)。形成技術(shù)標(biāo)準(zhǔn)多項(xiàng),包括行業(yè)標(biāo)準(zhǔn)2項(xiàng),地方標(biāo)準(zhǔn)3項(xiàng),企業(yè)標(biāo)準(zhǔn)2項(xiàng),團(tuán)體標(biāo)準(zhǔn)14項(xiàng)。 將(21)式代入條件(11),得到 (22) (23) (24) 進(jìn)一步化簡(jiǎn)得 (25) 或 (26) 令k(α-2μα)=ω,則k=ω/(α-2μα),(26)式可化為 (27) 解超越方程(27)可求出各能量,結(jié)果表明,若勢(shì)阱內(nèi)有束縛態(tài)能量是量子化的,勢(shì)阱內(nèi)至少有一個(gè)束縛態(tài)的基態(tài)能的條件是 作出函數(shù)y=|sinω|和函數(shù)y=Pω的圖像,其交點(diǎn)即為超越方程(27)的解 圖2 超越方程(27)圖解示意圖 3運(yùn)用mathematica作圖顯示δ勢(shì)壘的影響 添加δ勢(shì)壘后,能級(jí)的相關(guān)公式為 (29) 令n=log2H,取K1= 10不變, 運(yùn)用mathematica求解。 3.1勢(shì)壘位置的影響 當(dāng)n為0,1,2,3,……,10,μ分別取0.1到0.9之間的數(shù)值時(shí),計(jì)算K的數(shù)值解(只取基態(tài)值),結(jié)果如圖3所示。 圖3 K隨μ的變化曲線 由圖3可以看出:當(dāng)n=0時(shí)H=1,即(勢(shì)壘很低時(shí),μ值的變化對(duì)基態(tài)能級(jí)的影響并不大,隨著n的增大,μ值的影響也越明顯,當(dāng)μ處于0.55左右時(shí)對(duì)基態(tài)能級(jí)的影響最大,兩側(cè)逐漸減小。 3.2勢(shì)壘強(qiáng)度的影響 當(dāng)μ分別取0.1 ,0.2,……,0.9之間的數(shù)值,n為0,1,2,3,……,10時(shí),計(jì)算K的數(shù)值解(只取基態(tài)值)如圖4所示。 圖4 K隨n的變化圖形 由圖4知,在一定范圍內(nèi)K值隨著n值的增大而增大,而當(dāng)n增大到某個(gè)值或減小到某個(gè)值時(shí)K值達(dá)到穩(wěn)定不再變化。K的最小值與μ無(wú)關(guān)約為2.85,而K的最大值隨著μ的不同而有所不同。 4特殊情形 4.1情形一 當(dāng)n→-∞時(shí)H→0,此時(shí)模型變?yōu)橐痪S半無(wú)限深勢(shì)阱。由上文討論的不含勢(shì)壘的一維半無(wú)限深勢(shì)阱的情況可知,與能級(jí)有關(guān)的表達(dá)式為 (36) 同樣,取K1= 10,求得基態(tài)時(shí)K≈2.852 3,這與圖4中n→-∞時(shí)所得結(jié)果一致。 4.2情形二 表1 又由一維半無(wú)限深勢(shì)阱能級(jí)的相關(guān)公式得kcot[k(1-μ)a]=-κ,即無(wú)量綱化后為 同樣,取K1= 10,運(yùn)用mathematica求得μ取不同的值時(shí)對(duì)應(yīng)的基態(tài)K值如表2所示。 表2 綜上所述,當(dāng)μ取不同的值時(shí),整個(gè)一維半無(wú)限深勢(shì)阱中當(dāng)n→∞時(shí)對(duì)應(yīng)的基態(tài)K值如表3所示。 表3 這與圖4中n→∞時(shí)所得結(jié)果一致。 當(dāng)μ=1/2,V1=∞,即K1=∞時(shí),我們的模型成為中央有δ勢(shì)壘的無(wú)限深勢(shì)阱,將條件代入(29)式得到 (33) (34) (35) 這個(gè)結(jié)果與文獻(xiàn)[7]所得結(jié)果完全一致。 5結(jié)束語(yǔ) 通過(guò)理論推導(dǎo)與數(shù)值分析,研究了在添加δ勢(shì)壘的一維半無(wú)限深勢(shì)阱中運(yùn)動(dòng)的粒子的能級(jí)的影響因素,得到了該勢(shì)能下的波函數(shù)和能級(jí)的相關(guān)公式。對(duì)于給定勢(shì)壘高度K1的一維半無(wú)限深勢(shì)阱,δ勢(shì)壘的添加會(huì)使束縛態(tài)能級(jí)的量值增加,能級(jí)個(gè)數(shù)減少;勢(shì)壘的強(qiáng)度與位置對(duì)能級(jí)都會(huì)產(chǎn)生影響,當(dāng)勢(shì)壘處于勢(shì)阱中心偏右位置時(shí)能級(jí)最大,在K1=10的情況下,μ≈0.55,δ勢(shì)壘的強(qiáng)度H越大,位置的影響越明顯;當(dāng)δ勢(shì)壘的位置一定時(shí),δ勢(shì)壘的強(qiáng)度H越大,能級(jí)越大。當(dāng)H→∞時(shí)勢(shì)阱分裂為一維無(wú)限深勢(shì)阱和一維半無(wú)限深勢(shì)阱兩部分,并且由這兩部分求的基態(tài)能級(jí)與本文公式(29)中當(dāng)H→∞時(shí)求得的結(jié)果一致;適當(dāng)選取參數(shù)發(fā)現(xiàn)文獻(xiàn)[5-7]中的結(jié)果都是本文結(jié)果的特例,這表明了本文結(jié)論的普遍性和正確性。 參考文獻(xiàn): [1] M. Willem. Minimax theorems[M]. Basel Boston Berlin: Birkhaüser,1996. [2] I. Kuzin, S. Pohozaev. Entire solutions of semilinear elliptic equations[M]. Basel Boston Berlin: Birkhaüser,1997. [3] T.Tao,M.Visan,Xiaoyi Zhang.The nonlinear Schr?inger equation with combined power-type nonlinearities[J].Communications in Partial Differential Equations, 2007,32(8):1281-1343. [4] L.Ma,J.Wang. Inhomogeneous problem for the Ginzburg-Landau equation on two dimensional compact manifolds[J]. Dynamics of Partial Differential Equations, 2010, 7(2):175-185. [5] 曾謹(jǐn)言.量子力學(xué)[M].北京:科學(xué)出版社,1982:69. [6] 史守華.量子力學(xué)考研輔導(dǎo)教材[M]. 北京:清華大學(xué)出版社,2003:4-5. [7] 李明明,陳崗.無(wú)限深方勢(shì)阱附加δ勢(shì)后的定態(tài)解[J].山東師范大學(xué)學(xué)報(bào),2004,12(4):96-97. [8] 井孝功,陳碩,趙永芳.方形勢(shì)與δ勢(shì)解的關(guān)系[J].大學(xué)物理,2004,12(12):18-20. [5] 錢(qián)伯初,曾謹(jǐn)言.量子力學(xué)習(xí)題精選與剖析[M] .2版. 北京:科學(xué)出版社,1999:2-4. [6] 周世勛.量子力學(xué)教程[M] .1版.北京:高等教育出版社,1979:19-20. [7] 朱文熙,王玉平.對(duì)稱(chēng)雙方勢(shì)阱無(wú)簡(jiǎn)并[J] .大學(xué)物理,1999,2(2):33. [8] 尹健武,馮杰,陳嬌. 一維高低不對(duì)稱(chēng)方勢(shì)阱問(wèn)題的數(shù)值方法[J] .黃岡師范學(xué)院報(bào),2005,12(6):26-29. Research on the Effects of Additional Delta Barrier to One Dimensional Semi-infinite Deep Potential Well TANG Yi-jia,HAN Xiu-lin (School of Physics and Electronic engineering,F(xiàn)uyang Teachers College, Fuyang 236037, China) Abstract:By adding the delta barrier of one dimensional semi-infinite deep potential well,and solving the schrodinger equation, the related formula of particle movement of wave function and energy level are obtained. Through analysis we found that the delta barrier to add and its change on the energy level of the position and strength are affected. Contrast does not contain the delta barrier in one dimensional semi-infinite deep trap energy level. In addition, we explore the delta barrier to add to the impact of the original energy level, and use the Mathematica graphic visual indication to this effect. Key words:δ potential barrier, one dimensional semi-infinite deep potential well, energy level 文章編號(hào):1007-4260(2015)03-0060-04 中圖分類(lèi)號(hào):O469 文獻(xiàn)標(biāo)識(shí)碼:A DOI:10.13757/j.cnki.cn34-1150/n.2015.03.017 作者簡(jiǎn)介:唐義甲,男,安徽樅陽(yáng)人,碩士,阜陽(yáng)師范物理與電子工程學(xué)院助理實(shí)驗(yàn)師,研究方向?yàn)榉蔷€性光學(xué)材料、高能粒子束輻照改性及防護(hù)。 基金項(xiàng)目:國(guó)家自然科學(xué)基金項(xiàng)目( 11273008) ,阜陽(yáng)師范學(xué)院教學(xué)研究項(xiàng)目(2012JYXM61),(2013ZYJS08)和阜陽(yáng)師范學(xué)院基礎(chǔ)教育研究項(xiàng)目(2012JCJY21)。 收稿日期:2015-01-11 網(wǎng)絡(luò)出版時(shí)間:2015-8-25 15:40網(wǎng)絡(luò)出版地址:http://www.cnki.net/kcms/detail/34.1150.N.20150825.1540.017.html
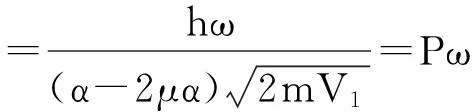
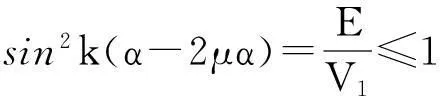

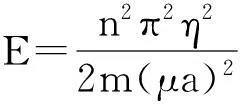



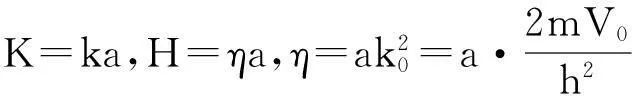
 安慶師范大學(xué)學(xué)報(bào)(自然科學(xué)版)2015年3期
安慶師范大學(xué)學(xué)報(bào)(自然科學(xué)版)2015年3期
- 安慶師范大學(xué)學(xué)報(bào)(自然科學(xué)版)的其它文章
- 國(guó)內(nèi)節(jié)能減排評(píng)價(jià)指標(biāo)體系及構(gòu)建方法述評(píng)
- 高三數(shù)學(xué)復(fù)習(xí)的策略探討
- 實(shí)變函數(shù)中集合外測(cè)度三種定義的等價(jià)性
- 開(kāi)關(guān)磁阻電機(jī)調(diào)速系統(tǒng)的設(shè)計(jì)與實(shí)現(xiàn)
- 非均勻圓環(huán)形薄膜的離散模型軸對(duì)稱(chēng)振動(dòng)的定性性質(zhì)
- 基于場(chǎng)景切換的B幀量化參數(shù)分配方法
