諧振式光子晶體光纖陀螺環路建模與仿真

李建華，于懷勇，雷 明，吳衍記

(北京自動化控制設備研究所，北京100074)

?

諧振式光子晶體光纖陀螺環路建模與仿真

李建華，于懷勇，雷 明，吳衍記

(北京自動化控制設備研究所，北京100074)

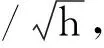
諧振式光子晶體光纖陀螺；PI控制器；相對頻率噪聲；隨機游走系數

0 引言

隨著武器裝備系統的發展，特別是在小型化飛航導航、高精度常規武器等領域，對小型化下高精度光纖陀螺提出了新的需求，迫切需要一種新型的小體積、高精度光纖陀螺產品。諧振式光纖陀螺原理上利用長度僅為幾米至十幾米的光纖諧振腔就可以實現很高的精度[1]，成為光纖陀螺小型化、高精度方向發展的潛力方案之一，也引起了研究者的廣泛關注。但國內外研究單位三十幾年的研究表明：非線性克爾噪聲、熱致偏振耦合噪聲及光源相對頻率噪聲等因素嚴重制約了諧振式光纖陀螺的技術發展，其性能還不能滿足應用需求[2-3]。

隨著光子晶體光纖技術的發展，諧振式光子晶體光纖陀螺越來越受到人們的重視，為抑制非線性克爾噪聲與熱致偏振耦合噪聲提供了一條嶄新的技術途徑。目前，國外光子晶體光纖陀螺研究的代表單位是美國Honeywell公司、Northrop Grumman公司、Standford大學等，其中Honeywell公司和Northrop Grumman公司將諧振式光子晶體光纖陀螺列到光纖陀螺中長期發展規劃中，作為小型化下實現高精度光纖陀螺的主要技術方案[4]。

在非線性克爾噪聲與熱致偏振耦合噪聲受到抑制的情況下，光源相對頻率噪聲成為制約諧振式光子晶體光纖陀螺精度的主要因素，對隨機游走系數造成嚴重影響。為有效地改善系統的動態和精度指標，引入PI控制器設計回路控制系統，PI控制器在控制領域有著最廣泛的應用[5]。本文通過設計PI控制器的控制參數，對環路模型進行仿真與優化。在此基礎上，通過對檢測帶寬的設計，對相對頻率噪聲進行抑制，以減小隨機游走系數，提高諧振式光子晶體光纖陀螺系統的檢測精度，最終對不同精度諧振式光子晶體光纖陀螺設計提供指導。

1 基本原理

諧振式光子晶體光纖陀螺的檢測原理為光學Sagnac效應，主要是通過敏感順、逆時針兩方向的頻率差Δf來實現旋轉角速度Ω檢測[6]。諧振頻率差Δf正比于旋轉角速度，表示為

(1)

其中，D為環形諧振腔的直徑，n為光纖折射率，λ為輸入光的工作波長。

圖1給出了諧振式光子晶體光纖陀螺系統框圖。諧振式光子晶體光纖陀螺必須鎖定順、逆時針至少一個方向傳播的光波，使其始終處于諧振狀態。在逆時針方向上，光束通過分束器C1進入光子晶體光纖環形諧振腔，再通過耦合器C4由光電探測器PD1進行檢測，進而由伺服回路驅動光源中心頻率的改變，使其鎖定在諧振腔逆時針諧振頻率上；同理，在順時針方向上，光束從諧振腔輸出之后通過耦合器C3，由光電探測器PD2轉化為電信號，并在第二個相敏解調器中進行解調。解調器輸出的信號通過與光源的光波頻率進行比較，給出了諧振腔相對于慣性空間旋轉的幅值和方向。

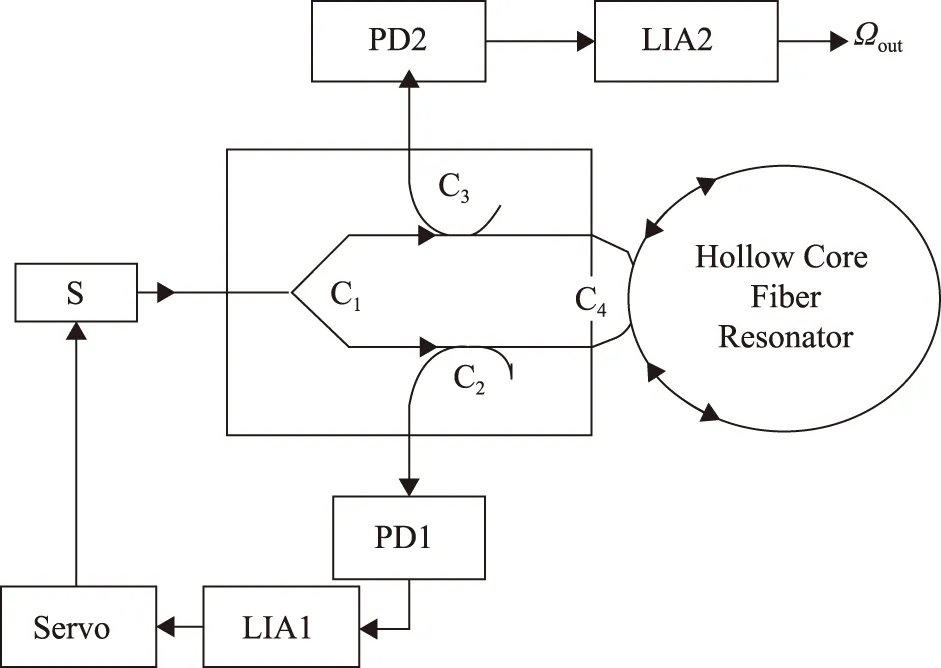
圖1 諧振式光子晶體光纖陀螺系統框圖Fig.1 The structure of resonatorphotonic crystal fiber optical gyro

2 陀螺環路模型建立

2.1 陀螺環路理想狀態模型

為便于系統分析，需建立諧振式光子晶體光纖陀螺環路模型，順時針和逆時針方向環路結構相似，可以進行同等等效。理想情況下，在順時針(CW)環路模型中，可以將光束頻率調制及經過諧振腔到光電探測器輸出的過程等效為增益KCW，將解調(DM)電路的增益等效為K1，將低通濾波器(Filter)等效為一階慣性環節。根據以上分析，建立諧振式光子晶體光纖陀螺環路簡化模型，如圖2所示。

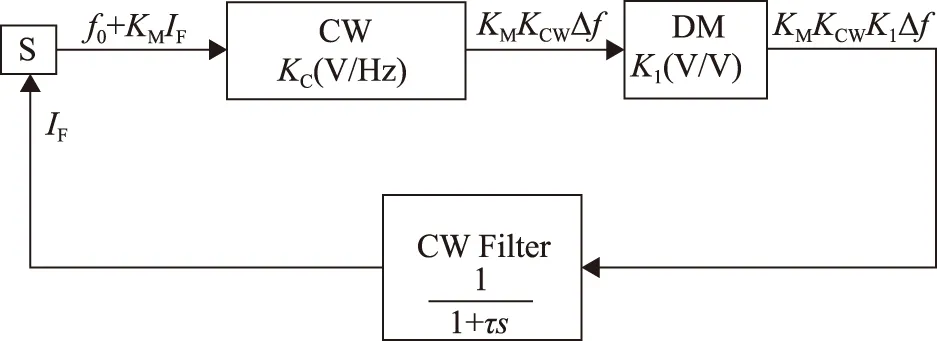
圖2 諧振式光子晶體光纖陀螺順時針理想環路模型Fig.2 The ideal clockwise loop model ofresonator photonic crystal fiber optical gyro

在諧振式光子晶體光纖陀螺工作的過程中，光源發出的激光(中心頻率為f0)經過相位調制器之后，耦合進入環形諧振腔，形成順時針方向上的諧振光束。順時針方向的光波在環形諧振腔中環繞多次傳輸之后，由光電探測器轉化成電信號輸出。鎖相放大器對光電探測器輸出的電信號進行解調，解調輸出信號作為反饋回路的誤差信號，將光源的中心頻率調節為f0+KMIF(KM為激光器頻率調制系數，IF為控制激光器頻率的反饋電流信號)。只要存在解調輸出信號，反饋伺服將一直運行，直到光源的中心頻率鎖定在諧振腔順時針方向的諧振頻率上達到環路的平衡狀態。根據上述順時針工作機理的分析，順時針環路開環傳遞函數表示為

(2)

式中，KL=KMKCWK1稱為環路增益，τ為濾波器時間常數。可以看出諧振式光子晶體光纖陀螺系統為一典型的慣性系統。對于諧振式光子晶體光纖陀螺，雖然能夠有效抑制非線性克爾噪聲與熱致偏振耦合噪聲，但光源的相對頻率噪聲會嚴重影響隨機游走系數，從而降低陀螺對旋轉角速率的測量精度[4]。

2.2 陀螺相對頻率噪聲環路抑制模型

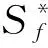
(3)

其中，G為環路系統頻率響應的幅值，Sf為激光光源的初始頻率噪聲功率譜密度。Sf由洛倫茲激光線性光譜的半高全寬(FWHM)Δν決定

(4)

由式(3)與式(4)可得

(5)

系統頻率響應的幅值是頻率的函數。對于一階環路來說，頻率每降低十倍頻程，環路增益會增加20dB，相應的頻率噪聲會隨著頻率的降低而減小。單純的慣性環節無法消除階躍響應的穩態誤差[7]，也就無法較好地抑制相對頻率噪聲。因此，需要通過設計PI控制器提高系統的型別，來抑制可控頻率噪聲功率譜密度，此時順時針環路新的模型如圖3所示。

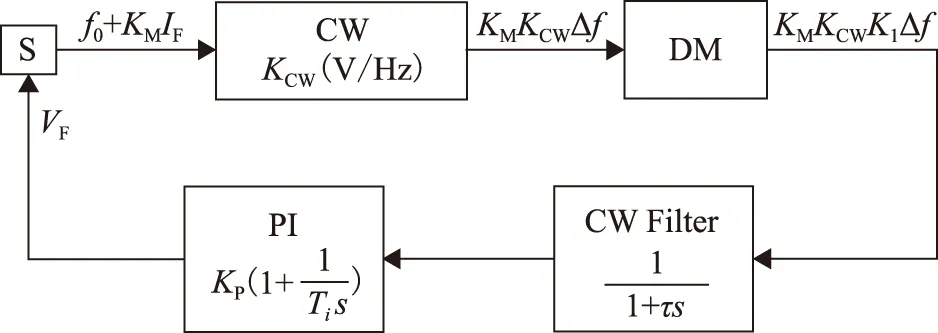
圖3 諧振式光子晶體光纖陀螺順時針環路相對頻率噪聲抑制模型Fig.3 The relative frequency noise control model of resonator photonic crystal fiber optical gyro clockwise loop

圖3中PI控制器的數學描述為

(6)

式中，u(t)為控制器輸出信號；e(t)=x(t)-o(t)為系統誤差信號，x(t)為系統輸入信號，o(t)為系統輸出信號；Kp為比例系數；Ti為積分時間常數。通過調節比例系數Kp可以降低系統的穩態誤差，而Ti決定積分作用強弱，積分環節能起到提高系統無差度的作用。因此，可以通過調節PI控制器的系數Kp和Ti來控制頻率響應的幅值，進而實現對可控頻率噪聲功率譜密度的控制。

PI控制器的傳遞函數可以表示為

(7)

此時，系統開環傳遞函數表示為

(8)

系統的閉環傳遞函數及開環幅頻響應的值為：

(9)

(10)

式中，定義K=KPKL為新的環路增益。加入PI控制器之后，系統由慣性系統變為二階系統，提高了系統的型別[7]。

3 環路模型仿真與優化

在模型仿真的過程中關鍵是PI控制器參數的選取，包括比例和積分兩個環節的參數Kp和Ti。從PI控制器對環路的影響考慮，PI參數選擇應該滿足超調量較小、帶寬較大的原則，超調量也不能太小，否則會增大系統阻尼影響響應時間，故超調量一般選取為5%～15%[7]。

對于二階系統，跟據式(9)可求得無阻尼振蕩頻率ωn和阻尼比ξ：

(11)

(12)

阻尼比ξ與超調量σP之間的表達式為

(13)

控制系統的閉環頻率特性可以由閉環傳遞函數得出，并且可以寫成

(14)

其中，A(ω)為閉環幅頻特性。由式(8)可知開環傳遞函數中含有串聯積分環節，則閉環幅頻特性在ω=0處的值為A(0)=1。當閉環幅頻特性降至0.707A(0)時，對應的角頻率ωb為閉環系統的帶寬[7]。此時系統閉環幅頻特性的值為

(15)

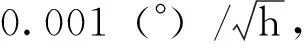
系統的幅頻響應如圖4所示，通過對頻率響應的分析可知，系統帶寬分別為39.1kHz、38.3kHz、37.4kHz、36.7kHz、36.1kHz、35.6kHz，可知隨著超調量的增加，系統帶寬越來越小，諧振式光子晶體光纖陀螺系統能夠獲得大帶寬，帶寬越大，響應時間越小，預示著系統有較小的響應時間；系統的相角裕度分別為69°、67°、63°、59°、57°、55°，可見隨著超調量的增加，系統的相角裕度越來越小，相角裕度是控制系統的重要指標，反映閉環系統遠離臨界穩定狀態的程度，通常要求大于30°，故該諧振式光子晶體光纖陀螺系統能夠得到較大的相角裕度。

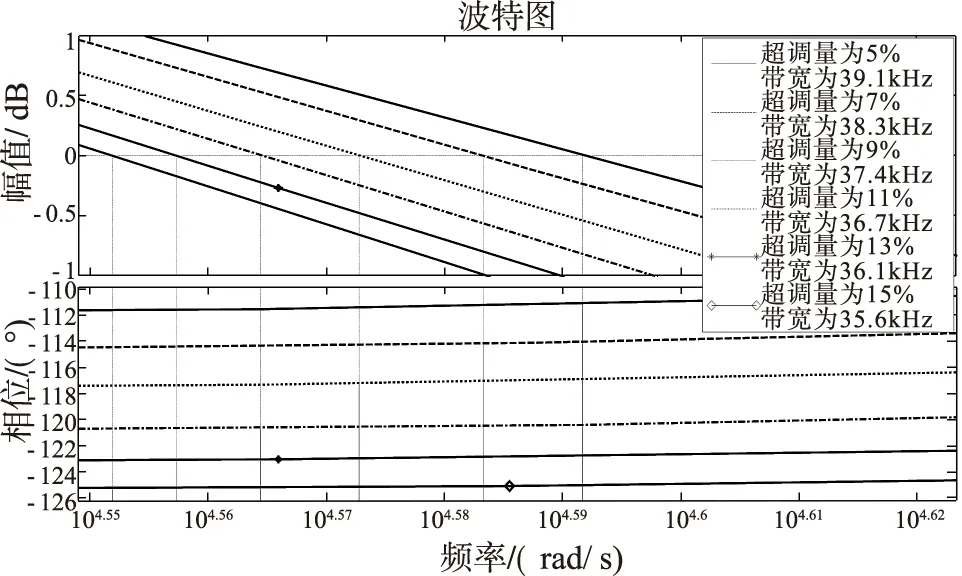
圖4 系統幅頻響應示意圖Fig.4 Magnitude response of the system

設計的諧振式光子晶體光纖陀螺系統帶寬和相角裕度均能滿足要求，可以用閉環系統的單位階躍響應曲線，進一步檢驗系統的性能。系統的階躍響應如圖5所示，在不同的參數下諧振式光子晶體光纖陀螺系統都能很好地跟蹤上階躍響應，響應時間為1.3×10-4s(±3%)；系統的超調量越來越大，從8%增加到17%，超調量過大會造成陀螺的偽轉動，使檢測精度降低。綜上可知，當將超調量設定為5%進行仿真時系統的性能最優，此時K=1.68，Ti=2.5×10-5s，得到的帶寬為39.1kHz，且響應時間為1.24×10-4s，超調量為最小的8%，環路無震蕩，滿足諧振式光子晶體光纖陀螺系統設計的性能指標要求。

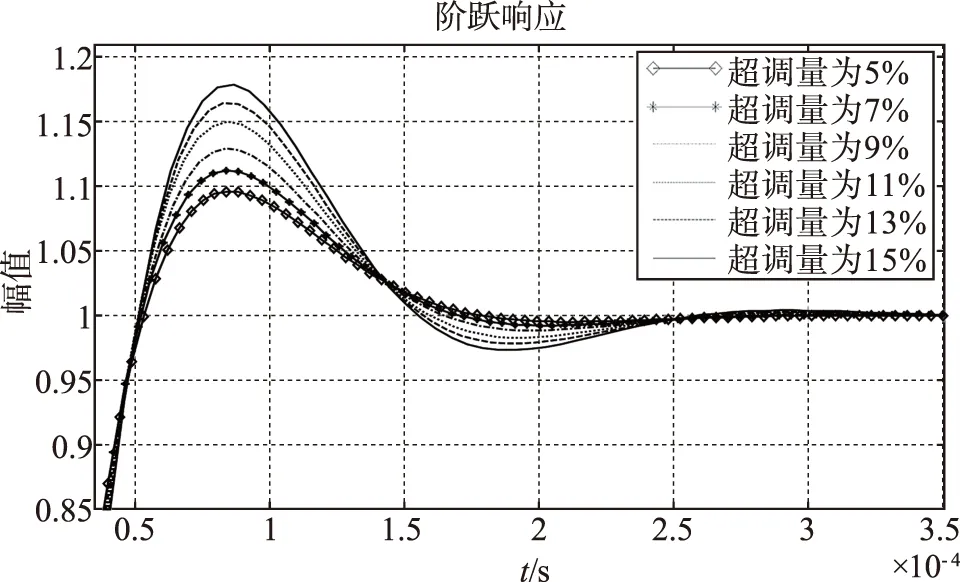
圖5 系統階躍響應示意圖Fig.5 Step response of the system

獲得理想閉環系統參數之后，進行檢測帶寬的設計，實現對隨機游走系數的控制，通過推導得到隨機游走系數與檢測帶寬及可控頻率噪聲功率譜密度之間的關系為

(16)

其中，ωf為檢測帶寬。因此，利用式(5)、式(10)、式(16)計算可得系統檢測帶寬與隨機游走系數之間的關系如圖6所示。

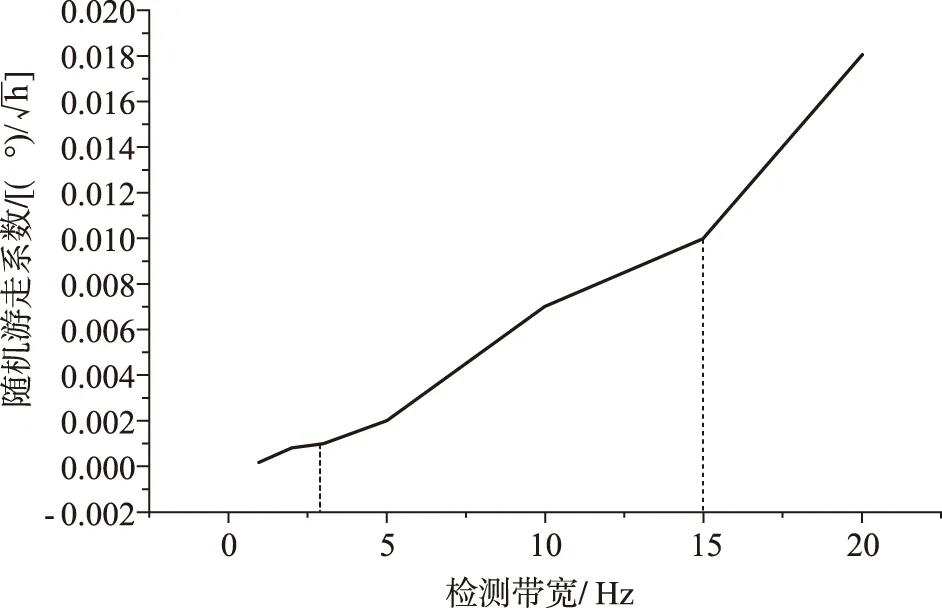
圖6 檢測帶寬與隨機游走系數關系圖Fig.6 The relationship bwtweendetecting bandwidth and RWC

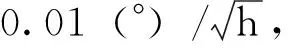
4 結論

本文對諧振式光子晶體光纖陀螺環路模型進行了仿真與優化，并進行檢測帶寬的設計，得到如下結論：

1)通過對相對頻率噪聲的分析，將經典控制理論運用于諧振式光子晶體光纖陀螺模型中，引入PI控制器，與理想情況下的一階慣性環節構成反饋控制回路；

2)經過優化PI參數，得到諧振式光子晶體光纖陀螺模型的系統帶寬為39.1kHz，響應時間為1.24×10-4s，超調量為8%，滿足系統動態性能指標的要求；

3)將仿真得到的結果應用于諧振式光子晶體光纖陀螺模型中，根據諧振式光子晶體光纖陀螺性能指標的要求，通過檢測帶寬的設計實現不同精度諧振式光子晶體光纖陀螺，當檢測帶寬小于15Hz，諧振式光子晶體光纖陀螺精度滿足戰術級陀螺的要求，當檢測帶寬小于3Hz，諧振式光子晶體光纖陀螺精度滿足導航級陀螺的要求。

[1] 張維敘.光纖陀螺及其應用[M].北京：國防工業出版社，2008：1-20.

[2] Glen A Sanders，Lee K Strandjordand，Tiequn Qiu.Hollow Core fiber optic ring resonator for rotation rensing[J]. OSA，2006：1-2.

[3] 于懷勇，吳衍記，雷明，李宗利.硅基波導諧振腔特性分析與實驗研究[J].導航定位與授時，2015，2(2)：46-53.

[4] Glen A Sanders，Scottsdale，AZ(US)；Lee K Str-andjord，Tonka Bay，MN(US).System and met-hod forstabilizing light sources in resonator gyro[P].U.S.Patant NO.7372574，2008.

[5] 顏文俊，陳素琴，林峰.控制理論CAI教程[M].北京：科學出版社，2003：212-217.

[6] 孫眾.諧振式激光學陀螺雙路閉環信號檢測技術研究[D]. 碩士學位論文.杭州，浙江大學，2012.

[7] 裴潤，宋申民.自動控制原理[M].哈爾濱：哈爾濱工業大學出版社，2006：74-271.

Modeling and Simulation of Resonator Photonic Crystal Fiber Optical Gyro Structure Based on Multi-source

LI Jian-hua，YU Huai-yong，LEI Ming，WU Yan-ji

(Beijing Institute of Automatic Control Equipment，Beijing 100074，China)

Resonator photonic crystal fiber optical gyro； PI controller； The relative frequency noise； The random walk coefficient

2015 - 04 - 09；

2015 - 04 - 28。

李建華(1990 - )，男，碩士，主要從事光纖陀螺的研究。

TP273

A

2095-8110(2015)05-0058-05