多分類敏感問題RRT模型下分層三階段抽樣的統(tǒng)計(jì)方法及應(yīng)用*
蘇州大學(xué)公共衛(wèi)生學(xué)院(215123) 楊少春 高 歌范玉波 陳科錦 杜俏俏 陳向宇 傅 穎 施佳琛
多分類敏感問題RRT模型下分層三階段抽樣的統(tǒng)計(jì)方法及應(yīng)用*
蘇州大學(xué)公共衛(wèi)生學(xué)院(215123) 楊少春 高 歌△范玉波 陳科錦 杜俏俏 陳向宇 傅 穎 施佳琛
目的為實(shí)際需要的多分類敏感性問題的復(fù)雜抽樣提供信度高效度高的調(diào)查方法及其統(tǒng)計(jì)公式;為制訂艾滋病預(yù)防控制措施提供科學(xué)依據(jù)。方法根據(jù)抽樣理論、RRT模型、全概率公式等理論方法推導(dǎo)統(tǒng)計(jì)公式;對(duì)北京市MSM人群進(jìn)行實(shí)例調(diào)查;用SAS編程分別對(duì)6個(gè)調(diào)查指標(biāo)各類別,各模擬多分類敏感問題RRT模型下分層三階段抽樣調(diào)查100個(gè)樣本,按本文給出的統(tǒng)計(jì)公式計(jì)算100個(gè)總體比例的可信區(qū)間。結(jié)果推導(dǎo)出多分類敏感問題RRT模型下分層三階段抽樣各類別總體比例估計(jì)量及其方差的計(jì)算公式;調(diào)查得到北京市MSM人群6項(xiàng)敏感問題指標(biāo)各類別樣本比例及其標(biāo)準(zhǔn)誤。各指標(biāo)各類別各模擬得到的100個(gè)總體比例95%可信區(qū)間幾乎均包含其模擬總體比例。結(jié)論本文研究的敏感問題調(diào)查方法及其公式具有良好的信度和效度,值得推廣應(yīng)用;MSM人群具有艾滋病的高危性行為,應(yīng)加強(qiáng)對(duì)其的預(yù)防控制。
敏感問題 隨機(jī)應(yīng)答技術(shù)(RRT) (分層)三階段抽樣 MSM效度與信度
抽樣調(diào)查一直作為醫(yī)學(xué)科研及衛(wèi)生工作中的一種重要方法及獲取統(tǒng)計(jì)資料的重要手段[1-3]。在抽樣調(diào)查研究中,經(jīng)常會(huì)遇到各種各樣的敏感性問題。所謂敏感性問題是指高度私人機(jī)密性或大多數(shù)人認(rèn)為不便在公開場(chǎng)合表態(tài)及陳述的問題[4],例如:吸毒、賣淫、嫖娼、男男性行為、性病、艾滋病等。敏感性問題按總體的特征可分為分類特征敏感問題和數(shù)量特征敏感問題,分類特征敏感問題又分為兩分類敏感性問題和多分類敏感性問題[5]。隨機(jī)應(yīng)答技術(shù)(random ized response technique,RRT)巧妙地運(yùn)用一個(gè)隨機(jī)裝置,在保護(hù)個(gè)人隱私的情況下,通過概率計(jì)算估計(jì)敏感問題特征的比例或均值,消除減小調(diào)查對(duì)象回答敏感問題時(shí)的拒答或說謊偏倚。國外已將各種RRT廣泛使用于流產(chǎn)率、女性飲酒量以及偷稅漏稅等各類敏感問題的調(diào)查,并得到了較好的調(diào)查結(jié)果[6-10]。
在本團(tuán)隊(duì)研究前,國內(nèi)外關(guān)于敏感問題調(diào)查的研究,主要局限于簡(jiǎn)單隨機(jī)抽樣調(diào)查和隨機(jī)化裝置的改進(jìn)等理論研究[11-13]。本團(tuán)隊(duì)對(duì)非敏感問題各種復(fù)雜抽樣和敏感問題多種復(fù)雜抽樣的統(tǒng)計(jì)方法進(jìn)行過系列研究[14-15]。本文對(duì)敏感問題實(shí)際抽樣調(diào)查中常常采用的多分類敏感問題RRT模型下分層三階段抽樣:從數(shù)學(xué)上推導(dǎo)出其統(tǒng)計(jì)公式;在北京市男男性行為人群的調(diào)查中取得了成功的實(shí)際應(yīng)用效果;采用SAS編程進(jìn)行大樣本個(gè)數(shù)大樣本量的計(jì)算機(jī)模擬抽樣調(diào)查與分析,得到了高信度和高效度的評(píng)價(jià)結(jié)果。
多分類敏感問題RRT模型下分層三階段抽樣的統(tǒng)計(jì)方法
1.分層三階段抽樣方法
假定總體劃分成L層。第h層由N1h個(gè)一級(jí)單位組成;h層第i個(gè)一級(jí)單位由Ni2h個(gè)二級(jí)單位組成,h層平均每個(gè)一級(jí)單位包含2h個(gè)二級(jí)單位;h層第i個(gè)一級(jí)單位內(nèi)第j個(gè)二級(jí)單位包含Nij3h個(gè)三級(jí)單位,h層平均每個(gè)二級(jí)單位包含3h個(gè)三級(jí)單位,h層共有Nh個(gè)三級(jí)單位,總體中共有N個(gè)三級(jí)單位;這里,h=1,2,…,L;i=1,2,…,N1h;j=1,2,…,Ni2h。第一階段從h層隨機(jī)抽取n1h個(gè)一級(jí)單位;第二階段從h層第i個(gè)被抽中的一級(jí)單位內(nèi)隨機(jī)抽取ni2h個(gè)二級(jí)單位,平均從h層每個(gè)被抽中的一級(jí)單位內(nèi)隨機(jī)了抽取2h個(gè)二級(jí)單位;第三階段從h層第i個(gè)抽中的一級(jí)單位內(nèi)第j個(gè)抽中的二級(jí)單位中隨機(jī)抽取nij3h個(gè)三級(jí)單位,平均從h層每個(gè)抽中的二級(jí)單位中隨機(jī)抽取了3h個(gè)三級(jí)單位;這里h=1,2,…,L,i=1,2,…,n1h,j=1,2,…,ni2h。對(duì)每個(gè)被抽中的三級(jí)單位(人),采用多分類敏感問題隨機(jī)應(yīng)答模型進(jìn)行調(diào)查。
2.多分類敏感問題隨機(jī)應(yīng)答模型
設(shè)某敏感問題分為K種互斥的類別1,2,…,K。設(shè)計(jì)一隨機(jī)化裝置,如:將分別寫有0,1,2,…,K的K+1種按數(shù)量比例P0:P1:P2.…Pk(P0+P1+P2+…+Pk=1)的若干卡片混合放入袋中。無旁人在場(chǎng)時(shí)每個(gè)抽中的人(三級(jí)單位)有放回地從袋中隨機(jī)抽出一張卡片,若卡片上寫有0則真實(shí)回答自己屬于敏感問題的那一類的序號(hào);若卡片上寫有0以外的某個(gè)數(shù)則回答該數(shù)。
3.統(tǒng)計(jì)公式
(1)總體比例的估計(jì)量及其方差計(jì)算公式
假定pk為第k類敏感特征總體比例的估計(jì)量,ph-k為h層第k類總體比例ph-k的估計(jì)量,pih-k為h層第i個(gè)抽中一級(jí)單位第k類總體比例pijh-k的估計(jì)量,pih-k為h層第i個(gè)抽中一級(jí)單位內(nèi)第j個(gè)抽中二級(jí)單位第k類總體比例pijh-k的估計(jì)量,h=1,2,…,L,i=1,2,…,n1h,j=1,2,…,ni2h,k=1,2,…,nij3h。
根據(jù)抽樣理論,雖然原始分類多于兩類,但當(dāng)調(diào)查的目的是要估計(jì)總體中任何一類的個(gè)數(shù)占總數(shù)的比例時(shí),實(shí)質(zhì)上這些比例是按兩類得到的,所以兩分類的理論均適合于此種情況[2]。根據(jù)高歌、金丕煥給出的公式可得[1]:

(2)pijh-k的計(jì)算公式
設(shè)pijh-k為h層第i個(gè)一級(jí)單位第j個(gè)二級(jí)單位k類敏感問題的總體比例,mijh-k、λijh-k分別表示h層樣本中第i個(gè)一級(jí)單位第j個(gè)二級(jí)單位回答數(shù)字k的頻數(shù)、概率,根據(jù)全概率公式:
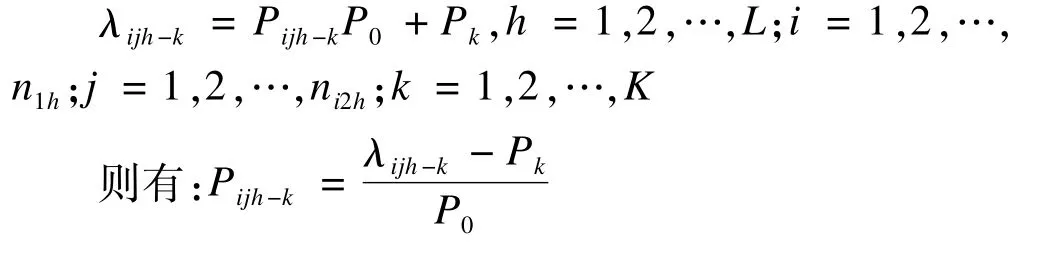
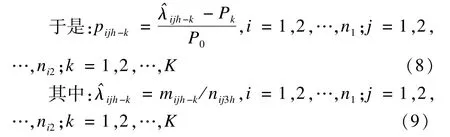
應(yīng)用實(shí)例
1.調(diào)查設(shè)計(jì)
(1)調(diào)查對(duì)象與調(diào)查指標(biāo)
調(diào)查對(duì)象為2010年9-10月出入北京市男同性戀活動(dòng)場(chǎng)所的15~49歲男男性行為(men who have sex with men,MSM)人群,總體數(shù)量約67750人。調(diào)查指標(biāo)1為男男性行為各方式的比例;調(diào)查指標(biāo)2為安全套全程使用情況各類別的比例;調(diào)查指標(biāo)3為HIV病毒檢測(cè)結(jié)果各類別的比例;調(diào)查指標(biāo)4為性病檢測(cè)結(jié)果各類別的比例;調(diào)查指標(biāo)5為最近一年男男商業(yè)性性行為次均費(fèi)用不同等級(jí)的比例;調(diào)查指標(biāo)6為安全套破損情況各類別的比例。
(2)抽樣方法
采用分層三階段抽樣,將北京市MSM人群按年齡分為15~29歲和30~49歲兩層,各自所占比例分別為W1=58.24%,W2=41.76%;在各層內(nèi)分別以北京的16個(gè)區(qū)縣為一級(jí)單位(N11=N12=16),以男同性戀活動(dòng)場(chǎng)所(如男同浴室、會(huì)所、酒吧、公園等)為二級(jí)單位(調(diào)查點(diǎn)),以男男性行為者作為三級(jí)單位。兩個(gè)年齡層內(nèi)平均每個(gè)區(qū)縣男同性戀人數(shù)分別約為2466人=1768人。第一階段從各年齡層的16個(gè)區(qū)縣中分別隨機(jī)抽取3個(gè)區(qū)縣(n11=n12=3);第二階段在所抽取的區(qū)縣各隨機(jī)抽取5個(gè)調(diào)查點(diǎn)(n=21=n22=5);第三階段從被抽中的5個(gè)調(diào)查點(diǎn)中共隨機(jī)抽取2062人,在各層內(nèi)平均從每個(gè)抽中調(diào)查點(diǎn)分別抽取了
(3)RRT模型
采用多分類敏感問題隨機(jī)應(yīng)答模型進(jìn)行調(diào)查,以商業(yè)性男男性行為平均費(fèi)用等級(jí)比例調(diào)查為例,設(shè)計(jì)一套隨機(jī)化裝置:將10個(gè)大小、重量、觸感完全相同的小球貼上數(shù)字標(biāo)簽,5個(gè)寫上數(shù)字0、剩余5個(gè)分別寫上數(shù)字1、2、3、4、5,即P0:P1:P2:P3:P4:P5為0.5:0.1:0.1:0.1:0.1:0.1(P0+P1+P2+P3+P4+P5=1),10個(gè)小球混合放入袋中;每個(gè)被抽中的三級(jí)單位有放回地從袋中隨機(jī)抽出一個(gè)小球,若抽中的小球上寫有0,真實(shí)回答自己“最近一年商業(yè)性男男性行為的平均費(fèi)用的等級(jí)序號(hào)k;若抽中的小球上寫有0以外的數(shù)字則直接回答該數(shù)字。
3.調(diào)查結(jié)果
按式(1)至(9)計(jì)算得:最近一年男男商業(yè)性性行為的次均費(fèi)用<200元、200~399元、400~599元、600元以上、無男男商業(yè)性性行為的比例分別為5.65%、4.86%、2.67%、6.48%、80.34%,其標(biāo)準(zhǔn)誤分別為0.70%、0.49%、0.57%、0.76%、2.20%;最近一個(gè)月男男肛交中從不全程使用安全套、有時(shí)全程使用安全套、每次全程使用安全套、沒有肛交的比例分別為6.46%、31.78%、51.81%、9.96%,其標(biāo)準(zhǔn)誤分別為0.77%、0.71%、0.95%、0.44%;最近一年HIV病毒檢測(cè)結(jié)果為陽性、陰性、結(jié)果不確定、沒有檢查過的比例分別為6.31%、78.67%、2.89%、6.45%,其標(biāo)準(zhǔn)誤分別為0.42%、1.96%、0.28%、0.45%;最近一年到正規(guī)醫(yī)療機(jī)構(gòu)性病檢測(cè)結(jié)果有性病、無性病、結(jié)果不確定、沒有檢查過的比例分別為16.79%、67.02%、6.25%、5.23%,其標(biāo)準(zhǔn)誤分別為0.66%、1.98%、0.46%、0.33%;男男性行為的方式為肛交、口交、其他的比例分別為65.83%、18.70%、15.47%,其標(biāo)準(zhǔn)誤分別為0.930%、0.658%、0.316%;安全套使用有破損、無破損、沒有使用安全套的比例分別為5.49%、70.26%、24.25%,其標(biāo)準(zhǔn)誤分別為0.57%、2.89%、1.89%。
信度效度評(píng)價(jià)
1.建立模擬總體
按照北京市的區(qū)縣數(shù)、北京市MSM活動(dòng)場(chǎng)所數(shù)、出入北京市男同性戀活動(dòng)場(chǎng)所的15~49歲MSM人數(shù)(67750人)及年齡構(gòu)成(15~29歲、30~49歲所占比例分別為W1=58.24%、W2=41.76%),以本文調(diào)查的6項(xiàng)多分類敏感問題各類別樣本比例、二項(xiàng)分布方差的數(shù)值作為模擬總體參數(shù),基于蒙特卡洛方法,用SAS編程建立模擬總體。模擬總體的一級(jí)單元為16個(gè)區(qū)縣,模擬總體的二級(jí)單元為男同性戀活動(dòng)場(chǎng)所(調(diào)查點(diǎn)),模擬總體的三級(jí)單元為男男性行為者。
2.模擬抽樣調(diào)查
模擬多分類敏感問題隨機(jī)應(yīng)答模型下分層三階段抽樣調(diào)查。第一階段模擬從16個(gè)區(qū)縣隨機(jī)抽取3個(gè)一級(jí)單元(區(qū)縣);第二階段抽樣從每個(gè)抽中的一級(jí)單元中隨機(jī)抽取5個(gè)二級(jí)單元(調(diào)查點(diǎn))。第三階段從被抽中的5個(gè)調(diào)查點(diǎn)中共隨機(jī)抽取2062人。
對(duì)敏感問題分層三階段抽樣的調(diào)查方法及其統(tǒng)計(jì)公式,各進(jìn)行100個(gè)樣本(每個(gè)樣本平均包含2533名模擬調(diào)查對(duì)象)的模擬抽樣調(diào)查,對(duì)模擬總體的抽樣由另外輸入的隨機(jī)數(shù)控制,根據(jù)這個(gè)隨機(jī)數(shù)計(jì)算機(jī)在模擬總體中進(jìn)行了分層三階段抽樣,并對(duì)抽中的三級(jí)單位進(jìn)行模擬調(diào)查。RRT調(diào)查過程的模擬再次用到了計(jì)算機(jī)產(chǎn)生確定范圍的隨機(jī)數(shù)的功能。例如,將北京市MSM人群按年齡分為15~29歲和30~49歲兩層,各自所占比例分別為W1=58.24%,W2=41.76%,根據(jù)模擬總體的比例,對(duì)虛擬調(diào)查對(duì)象進(jìn)行賦值,對(duì)于一個(gè)已經(jīng)被賦值為1的虛擬被調(diào)查者,計(jì)算機(jī)按一定比例單獨(dú)為它賦予一個(gè)0~3范圍的隨機(jī)整數(shù)(隨機(jī)化裝置),這相當(dāng)于此虛擬被調(diào)查者有放回地從袋中隨機(jī)摸出一個(gè)0~3范圍的任意標(biāo)號(hào)的小球。若計(jì)算機(jī)單獨(dú)為它賦予的隨機(jī)數(shù)是0,則真實(shí)回答自己屬于敏感問題的那一類的序號(hào),即是1;若被賦予的值是0以外的某個(gè)數(shù)則回答這個(gè)數(shù)。所得結(jié)果即為該虛擬被調(diào)查者的應(yīng)答值。每一個(gè)抽中的單位都產(chǎn)生了應(yīng)答值后,按照有關(guān)公式進(jìn)行統(tǒng)計(jì)計(jì)算,得到模擬調(diào)查結(jié)果計(jì)算樣本統(tǒng)計(jì)量及其估計(jì)方差、總體參數(shù)95%的置信區(qū)間。
3.信度和效度評(píng)價(jià)
對(duì)于本領(lǐng)域內(nèi)相關(guān)的一些研究結(jié)果進(jìn)行了相關(guān)的比較,商業(yè)性男男性行為比例為19.66%,略高于陳向宇[17]的19.11%;男男性行為的方式為肛交、口交的比例分別為65.83%、18.70%,高于杜俏俏[18]得出的肛交占60.95%、口交占16.85%;男男性行為時(shí)沒有使用安全套的比例為24.25%,高于于波[19]的沒有使用安全套的比例19.77%,并且最近一年HIV病毒檢測(cè)結(jié)果為陽性為6.31%,低于于波的最近一年HIV檢測(cè)的結(jié)果為陽性的比例8.03%;同時(shí),本文對(duì)于每個(gè)指標(biāo)都進(jìn)行了信度和效度評(píng)價(jià),分別對(duì)各調(diào)查指標(biāo)各類別100個(gè)模擬樣本,得到的100個(gè)總體比例95%可信區(qū)間,幾乎全部包含其模擬總體比例(真值),更加說明了測(cè)量結(jié)果的準(zhǔn)確性和可靠性。例如,對(duì)指標(biāo)1分類一(肛交),100個(gè)模擬樣本中有96個(gè)(樣本1、65、95、100除外)得到的該分類總體比例95%可信區(qū)間包含其模擬總體比例(真值),見圖1對(duì)指標(biāo)1分類二(口交),100個(gè)模擬樣本中有99個(gè)樣本(樣本95除外)得到的該分類總體比例95%可信區(qū)間包含其模擬總體比例(真值);對(duì)指標(biāo)1分類三(其他方式),100個(gè)模擬樣本中有97個(gè)(樣本1、4、95除外)得到的該分類總體比例95%可信區(qū)間包含其模擬總體比例(真值)。說明本文給出的多分類敏感問題隨機(jī)應(yīng)答技術(shù)模型下分層三階段抽樣的調(diào)查方法及其統(tǒng)計(jì)公式具有較高的效度,同時(shí)具有較高的信度(因幾乎所有的樣本均數(shù)均接近它們的均值)。
對(duì)調(diào)查指標(biāo)1的分類一,以樣本序號(hào)為橫坐標(biāo),以總體比例95%可信區(qū)間為縱坐標(biāo)繪圖,并以模擬總體比例做水平輔助線,見圖1。
討 論
1.本團(tuán)隊(duì)對(duì)多分類敏感問題RRT模型整群抽樣、二階段抽樣、分層兩階段整群抽樣等復(fù)雜抽樣的統(tǒng)計(jì)方法進(jìn)行過研究。在此研究基礎(chǔ)上,本文對(duì)多分類敏感問題RRT模型分層三階段抽樣,從數(shù)學(xué)上首次推導(dǎo)出各類別總體比例的估計(jì)量及其方差、估計(jì)方差的統(tǒng)計(jì)公式,具有統(tǒng)計(jì)理論方法學(xué)意義。
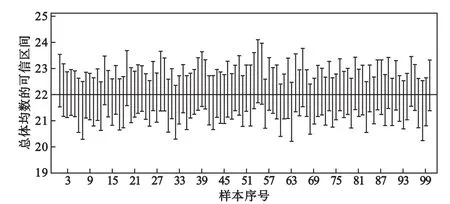
圖1 多分類敏感問題RRT分層三階段抽樣模擬
2.本團(tuán)隊(duì)研究之前,國內(nèi)外對(duì)敏感問題抽樣調(diào)查的信度與效度評(píng)價(jià)極少涉及。本文首次對(duì)多分類敏感問題RRT模型分層三階段抽樣的調(diào)查方法及其統(tǒng)計(jì)公式,采用SAS編程建立仿真模擬總體,進(jìn)行計(jì)算機(jī)大樣本個(gè)數(shù)(100個(gè))大樣本量(每個(gè)樣本含有2000多例)模擬抽樣,獲得高信度高效度的評(píng)價(jià)結(jié)論。說明本文研究的調(diào)查方法及其統(tǒng)計(jì)公式準(zhǔn)確可靠。
3.本文研究得北京市MSM人群:男男商業(yè)性性行為的比例高達(dá)19.66%,每次全程使用安全套的比例僅為51.81%,HIV陽性比例高達(dá)6.31%,有性病比例高達(dá)16.79%,肛交比例高達(dá)65.83%,未使用安全套的比例高達(dá)24.35%,安全套使用中有破損的比例高達(dá)7.25%。本文為有關(guān)部門制定性病、艾滋病預(yù)防控制規(guī)劃、措施提供了科學(xué)依據(jù)。說明本文研究的調(diào)查方法及其統(tǒng)計(jì)公式具有較大的實(shí)際意義。
4.評(píng)價(jià)結(jié)果表明,通過多分類敏感問題RRT模型分層三階段抽樣敏感問題調(diào)查方法能獲得大量真實(shí)數(shù)據(jù),將為有關(guān)部門制訂HIV/AIDS防治等社會(huì)、公共衛(wèi)生問題的政策、規(guī)劃提供科學(xué)的依據(jù)。
附 錄
模擬分層三階段抽樣并運(yùn)用多項(xiàng)選擇敏感問題隨機(jī)應(yīng)答模型進(jìn)行調(diào)查的宏程序代碼如下:





填入相應(yīng)的宏參數(shù),并執(zhí)行編寫的宏程序,即可獲得100次運(yùn)用多項(xiàng)選擇敏感問題隨機(jī)應(yīng)答模型對(duì)模擬抽樣的樣本進(jìn)行RRT調(diào)查所得的(每類別)100個(gè)樣本比例及其估計(jì)方差、(每類別)100個(gè)總體比例的95%可信區(qū)間,100個(gè)卡方檢驗(yàn)的P值。宏參數(shù)如下:
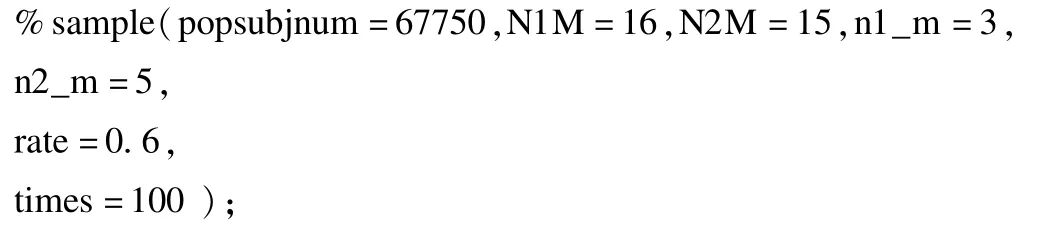
[1]高歌,金丕煥,王旭輝.分層三階段抽樣樣本大小的研究及應(yīng)用.中國衛(wèi)生統(tǒng)計(jì),2000,17(6):325-327.
[2]科克倫W.G.著,張堯庭,吳輝譯.抽樣技術(shù).中國統(tǒng)計(jì)出版社,1985:87.
[3]溫長(zhǎng)松.試述抽樣調(diào)查方法在歷史研究中的應(yīng)用.沈陽大學(xué)學(xué)報(bào),2006,18(1):40-41.
[4]王建華.實(shí)用醫(yī)學(xué)科研方法.人民衛(wèi)生出版社,2003:440-450.
[5]高歌,范玉波.敏感問題Simmons模型的(分層)整群抽樣研究.中國衛(wèi)生統(tǒng)計(jì),2008,25(6):562-565.
[6]Warner SL.Randomized response:a survey technique for eliminating evasive answer bias.JAm Stat Assoc,1965:60(309):63-66.
[7]Tourangeau R,Smith TW.Asking sensitive questions:The impact of date collection mode,question format,and question context.Public Opinion Quarterly,1996;(60):275-304.
[8]Stephen EE,Samuel H,Karen LD.Validity of Forced Responses in a Random ized Response Model.Sociological Methods&Research,1982,11(1):89-100.
[9]Liu PT,Chow LP.The efficiency of themultiple trial random ized response technique.Biometrics,1976,32(3):607-618.
[10]Chow LP,Gruhn W,Chang WP.Feasibility of the random ized response technique in rural Ethiopia.Am J Public Health,1979,69(3):273-276.
[11]孫山澤,孫明舉,段鋼.二項(xiàng)選擇敏感性問題調(diào)查的基本方法.?dāng)?shù)理統(tǒng)計(jì)與管理,2000,19(1):58-64.
[12]洪志敏,閆在在.一種定量敏感性問題的隨機(jī)化調(diào)查方法.內(nèi)蒙古工業(yè)大學(xué)學(xué)報(bào),2006,25(3):178-182.
[13]張權(quán),閆在在.二項(xiàng)抽樣下隨機(jī)化調(diào)查的比估計(jì)模型.內(nèi)蒙古工業(yè)大學(xué)學(xué)報(bào),2009,28(2):81-85.
[14]Wang M,Gao G.Quantitative sensitive question survey in cluster sampling and its application.Recent Advance in Statistics Application and Related Areas,Sydeny:Aussino Academ ic Publishing House 2008:648-652.
[15]Liu W,Gao G,Wang L.Stratified random sampling on simmons model for sensitive question survey.Data Processing and Quantitative Economy Modeling,Sydeny:Aussino Academ ic Publishing House,2010:22-26.
[16]陳向宇,高歌,于明潤,等.北京市商業(yè)性男男性行為Simmons模型調(diào)查.中國公共衛(wèi)生,2013,2:259-260.
[17]杜俏俏,高歌,靳宗達(dá),等.蒙特卡洛模擬在多分類敏感問題兩階段整群抽樣信度與效度評(píng)價(jià)中的應(yīng)用.中國衛(wèi)生統(tǒng)計(jì),2013,30(2):227-229.
[18]于波,高歌,賀志龍,等.北京市MSM人群RRT模型的兩階段抽樣調(diào)查.中國衛(wèi)生統(tǒng)計(jì),2012;06:351-352.
(責(zé)任編輯:劉 壯)
*:國家自然科學(xué)基金項(xiàng)目(項(xiàng)目編號(hào):81273188)
△通信作者:高歌,E-mail:gaoge@suda.edu.cn

