Aalen模型在醫學研究中的應用

曹志強王 楊李 衛△

Aalen模型在醫學研究中的應用

曹志強1，2王 楊1李 衛1△

Cox比例風險模型［1］是生存分析中最常用的模型，很多實際問題中的協變量并不滿足比例風險，而且協變量的效應可能隨時間變化。基于這些情況的考慮，Aalen提出了加法危險率模型［2-3］，Aalen模型是Cox模型的補充。Aalen模型一個重要的特征就是其回歸系數是隨時間變化的函數，這種函數沒有特定的形式，也不依賴任何參數假定。相對于Cox模型的半參數本質，Aalen模型是非參的，適合用于模型中含隨時間變化的協變量效應的研究。

原理與方法

Aalen模型的基本形式如下［4］：

其中α0（t）是基線函數，Zj（t）是第j個協變量在t時刻的值。αj（t），j＝1，…，k是回歸參數，其作用等價于Cox模型中的回歸系數。在實際中，直接估計αj（t）是困難的，因而轉向估計與其等價的累積回歸系數，定義如下：

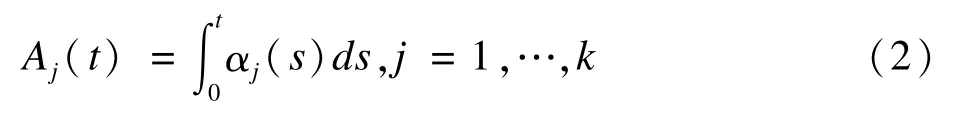
假設數據樣本的形式是［Tj，δj，Zj（t）］，j＝1，…，n，其中0＝T0＜T1＜T2＜…是排序好的時間，δj是判斷Tj是否刪失的示性變量是協變量向量。對于第j個個體，定義Yj（t）：如果個體j在t時刻是存活的，Yj（t）為1，否則為0。一般利用最小二乘法估計Aj（t），具體做法是先定義一個n×（k＋1）的設計矩陣X（t），其構造如下：對于X（t）的第i行，令Xi（t）＝Yi（t）（1，Zj（t）），即如果第i個個體在t時刻是存活的，那么Xi（t）＝（1，Zj1（t），…，Zjk（t）），否則Xi（t）就是k＋1維的0向量。設I（t）是一個n× 1維的向量，如果第i個個體在t時刻死了，那么I（t）的第i個元素為1，否則為0。基于上面的構造，累積回歸系數矩陣A（t）＝（A0（t），A1（t），…，Ak（t））T的最小二乘估計為：

在這個矩陣中，ID（t）是一個n×n的對角矩陣，其對角線元素等于I（t）。A（t）估計的最大時間Tmax是矩陣Xt（Ti）X（Ti）變為不可逆的最小時間。

為了檢驗協變量有無統計學意義，Aalen提出了下面的假設檢驗，原假設為：

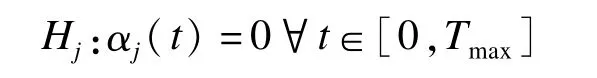
用向量U的第j個元素Uj檢驗Hj：

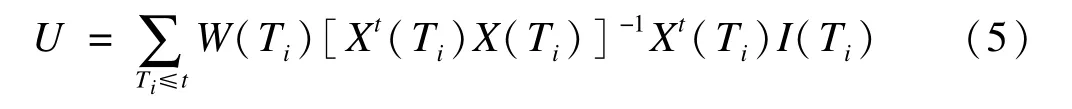
其中，W（t）是一個對角矩陣的權重函數，對角線元素為Wj（t），j＝1，2，…，k＋1。這種非參數檢驗方法只能檢驗Xt（Ti）X（Ti）是滿秩的這段時間。Aalen考慮了兩種權重函數，一種是W（t）等于t時刻存活的人數，另一種為下面的（6）式。

Aalen從理論上證明了檢驗統計量U服從漸近多元正態分布，用（6）式作為權重函數構造出來的檢驗統計量被稱之為TST。對于模型的擬合優度檢驗，Aalen提出了廣義殘差法和Arjas plot法。第j個個體的廣義殘差定義如下：

其中Sj是第j個個體的確定或者刪失時間，Z0＝（1，Z01，…，Z0k）T是0時刻協變量的取值。如果模型擬合的好，那么可視為來自標準指數分布的樣本。Arjas圖的思想是比較累計度（cumulative intensity）和真實死亡數，假如模型正確，那么它們的值應該差不多。具體做法是在Aalen模型中，對于每一確定時間Ti≤R，畫相對于i的圖像，如果模型正確，那么圖像近似為一條直線。

實例分析

一項以治療H1N1流感為目的的研究［5］，比較奧司他韋（達菲）和傳統中藥湯（麻杏石甘湯和銀翹散加減方）的治療效果，410例確診為輕癥H1N1流感的成年患者被隨機非盲分成4組：對照組、達菲組、中藥組、達菲加中藥組。目標變量time為從入組治療到結束的時間；status指發熱是否消退；age是患者的年齡；g2、g3、g4是三個啞變量，分別指患者服用的是達菲、中藥湯、達菲加中藥；fb48h是發病至入組時間是否大于48小時的二值變量；s2、s3、s4是三個中心啞變量。為了解決結點問題，將time每個值加上［0，1］之間的隨機數。

首先用age、g2、g3、g4、fb48h、s2、s3、s4作為協變量，進行Cox回歸，結果見表1。

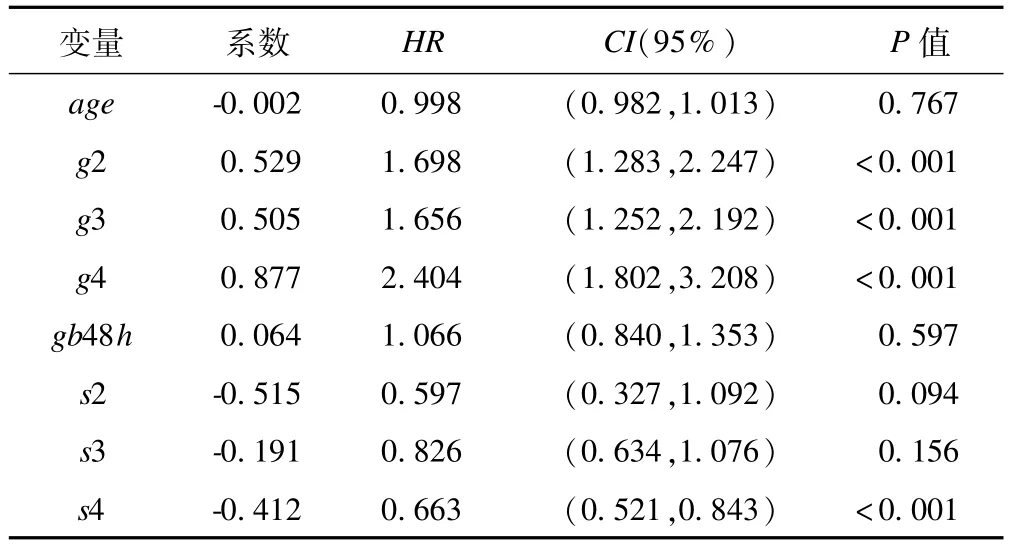
表1 Cox回歸結果

從表1可知，age、fb48h、s3無統計學意義，s2在0.1水平下有統計學意義，其他變量在0.05水平下均有統計學意義。本文研究的目標變量是發熱持續時間，相對不吃藥，如果吃了某種藥后發熱時間能夠顯著降低，說明該藥有效（此時HR＞1）。從結果來看，達菲、中藥湯、達菲加中藥都能有效治療H1N1流感。從表1還能得出，達菲的HR值比中藥湯的要高一點，達菲加中藥的HR值比單純達菲或中藥湯的都要高。然而，通過Wald檢驗發現，達菲相對中藥湯的HR值不顯著，但達菲加中藥相對達菲的HR是顯著的，HR置信區間為［0.072，0.871］，P＝0.014；達菲加中藥相對中藥湯的HR值也是顯著的，HR值的置信區間為［0.098，0.919］，P＝0.009。

用log-log圖檢驗Cox模型中的組別變量是否服從比例風險假定。可見中藥組的與其它三組有交叉，因此，模型的比例風險假定可能存在問題。文獻［6］指出，當Cox模型中的協變量不滿足比例風險時，可采用Aalen模型分析。

在具體運用Aalen模型之前，根據模型原理可以推斷出累積回歸系數的一些特征。如果Aalen模型中某個協變量的回歸系數是常數，即α（t）＝a，那么其在t時刻的累積回歸系數應為A（t）＝at這樣的一條直線。假設風險因子超過了t0時刻，比如t0＝20小時之后，對風險函數不再有影響，則其累積回歸系數在20小時后應該等于常數。如果變量在模型中有統計學意義，那么其累積回歸系數的置信區間不應該包含0。

表2 Aalen模型變量的檢驗結果

表2是用TST統計量檢驗Aalen模型中的變量有無統計學意義。從P值來看，age、fb48h、s3無統計學意義，其他變量均有統計學意義，這和Cox模型選擇變量的結果類似。

三組藥的累積回歸系數圖展示了三組藥在各時段如何影響風險函數。達菲的累積回歸系數在前38小時持續遞增，但超過38小時后斜率趨平且有降低趨勢，表明達菲對治療H1N1流感的效果主要體現在前38小時。中藥湯的累積回歸系數在前19小時顯著遞增，之后出現類似的轉平和減低趨勢，表明中藥湯的療效在前19個小時體現更為明確。至于達菲加中藥，其累積回歸系數在前38小時平穩增加，之后增加的趨勢減緩。因此達菲加中藥在前38小時的療效顯著，38小時后療效趨弱。

達菲、中藥湯、達菲加中藥的累積回歸系數的斜率均為正數，說明相對不吃藥，它們對治療H1N1流感都有效。有些學者［7］提出根據累積回歸系數的斜率來度量協變量的影響，目前這在文獻中不常見，在此我們不提倡根據斜率的大小就定量地確定達菲、中藥湯、達菲加中藥的療效到底有多好。

達菲加中藥的累積回歸系數圖的趨勢一直遞增，而達菲或中藥湯的在后面時段下降，以至于達菲在50小時時的置信下限包含0，中藥湯在37小時時的置信下限包含0。該信息是對各藥物特點（即持續有效時間）的體現，也說明樣本量隨時間減少，在一定程度上影響估計的精度。達菲、達菲加中藥比較好地符合Cox比例風險假定，這一點與之前log-log圖中所得的信息一致。

討 論

在醫學研究中，生存資料的多因素分析常采用Cox模型，其回歸系數度量的是相對風險。Aalen模型是從絕對風險的角度考慮生存時間和協變量之間的關系。在對兩種模型結果進行比較時，如果基于非參數模型在同一變量上給出的P值，大于半參數和參數模型（或前者無、而后者有統計學意義），而下結論Aalen模型不如Cox模型好，這是不合理的，其原因是兩個模型對應的檢驗本身不同。

實例分析表明，當Cox模型的比例風險假定不滿足時，我們可以用Aalen模型分析。在檢驗協變量有無統計學意義時，兩個模型得出了相似的結果。如果協變量在不同的時段對風險函數有不同的影響，成比例風險或者不成比例風險，用Aalen模型分析累積回歸系數圖是有幫助的。Aalen提倡將累加回歸系數圖作為診斷工具，觀察各變量在各時段如何影響風險函數。在本篇的例子中，通過觀察累積回歸系數圖，可以判斷藥物間的療效是否大致符合比例風險，以及了解治療H1N1流感中各藥物療效發揮時段的特點。可以說，累積回歸系數圖直觀展示了協變量影響風險函數的本質。

實際應用中，Aalen模型遠沒有Cox模型應用廣，一個原因是SAS和SPSS軟件中沒有現成Aalen模型的程序，而Cox模型的程序幾乎在每一款統計軟件中都早已存在。如今R軟件的兩個包survival和timereg提供了處理Aalen模型的程序，讓使用Aalen模型作為Cox模型的有效補充成為了可能。很多有關Aalen模型的文獻，包括Aalen的原創，都是提倡將Aalen模型視為Cox模型的補充，把兩個模型結合起來分析問題。總之，這兩個模型提供了數據的不同信息，它們不應該視為相互替代，而應是相互補充。這樣，我們對數據和問題就會有更全面和更深刻的認識和理解。

1.Cox DR.Regression models and life-tables.Journal of the Royal Statistical Society，Series B（Methodological），1972：187-220.

2.Aalen OO.A linear regression model for the analysis of life times.Statistics in medicine，1989，8（8）：907-925.

3.Aalen OO.Further results on the non-parametric linear regression model in survival analysis.Statistics in medicine，1993，12（17）：1569-1588.

4.Klein J，Moeschberger M.Survival Analysis：Techniques for Censored and Truncated Data，Springer，1997.

5.Wang C，Cao B，Liu QQ，et al.Oseltamivir compared with the Chinese traditional therapy maxingshigan-yinqiaosan in the treatment of H1N1 influenza：a randomized trial.Annals of Internal Medicine，2011，155（4）：217-25.

6.Abadi A，et al.Comparison of Aalen′s additive and Cox proportional hazards models for breast cancer survival：analysis of population-based data from British Columbia，Canada.Asian Pacific Journal of Cancer Prevention，2011，12：3113-3116.

7.Torner A.Proportional hazards and additive regression analysis of survival for severe breast cancer.Stockholm University，2004.

附錄：本文的R程序

（責任編輯：郭海強）

1中國醫學科學院，北京協和醫學院，國家心血管病中心，阜外心血管病醫院，心血管疾病國家重點實驗室（100037）

2北京師范大學數學科學學院

△通信作者：李衛，E-mail：liwei＠m rbc-nccd.com