葉片有限元分析中彈塑性過渡區應力奇異產生原因及解決方法

仲繼澤,徐自力,方宇,范小平,趙世全

?

葉片有限元分析中彈塑性過渡區應力奇異產生原因及解決方法

仲繼澤1,2,徐自力1,2,方宇3,范小平3,趙世全3

葉片在高溫、高壓蒸汽的推動下驅動汽輪機轉子轉動,將蒸汽的熱能轉化為機械能。為了提高單機的出力和機組的效率,長葉片和超長葉片不斷應用于汽輪機末級,例如:國內研發的全轉速鋼制1 092 mm葉片已應用在1 000 MW汽輪機中[1],并開發出了全轉速鋼制1 200 mm葉片;日本三菱重工開發了轉速為3 000 r/min的1 524 mm鋼制長葉片[2]。葉片長度增加,加上轉速高,葉片將承受更大的離心力,葉片根部會產生大應力,在應力集中部位甚至產生了塑性變形[3-4],由此降低了葉片疲勞壽命,且容易發生事故。因此,準確計算葉片,特別是葉根的應力水平,是葉片設計中至關重要的環節。

文獻[5]研究了葉根接觸應力計算的彈性有限元模型,即先用稀疏網格對整個葉片進行計算,然后對葉根接觸面局部進行第2次加密計算。文獻[6]研究了葉根和輪緣接觸邊界應力的典型特征。文獻[7]采用彈性有限元方法對某汽輪機末級長葉片進行了優化設計,使背弧側葉根圓角處最大應力由1 241 MPa下降到1 172 MPa,但該葉根圓實際上角最大應力位置已經發生屈服,進入塑性狀態。文獻[8]采用彈性和彈塑性有限元方法對某葉片進行了應力分析,得出彈性計算值和彈塑性計算值差別較大。文獻[9]發現采用彈塑性有限元法進行壽命評估更加符合實際。綜上所述,當葉片應力較大且局部進入塑性時,要準確計算葉片的應力必須采用彈塑性計算方法。采用彈塑性有限元法計算多個汽輪機末級長葉片應力時,在葉片根部彈塑性過渡區的應力計算值有時會大于塑性區的應力計算值,即應力奇異現象。這種應力奇異現象對葉片的安全評價會造成困擾,影響葉片疲勞、壽命評估的準確性。

針對葉片有限元分析中在彈塑性過渡區產生應力奇異的問題,本文研究了有限元法單元節點應力的計算過程,發現有限元法通常采用高斯積分點應力外推插值得到單元節點應力,當單元一部分位于彈性區、另一部分位于塑性區時,這種外插算法就會導致節點應力計算值大于結構的實際值,甚至超出彈塑性材料的屈服極限,使得節點應力計算值出現奇異,同時給出了消除葉片根部彈塑性過渡區應力奇異現象的方法。

1 彈塑性過渡區應力奇異現象

某葉片根部的三維實體及有限元網格見圖1。假定材料為理想彈塑性的,彈性模量為2.1×105MPa,泊松比為0.3,屈服極限為800 MPa,密度為7 850 kg/m3,材料的應力應變曲線見圖2。在葉根齒承載面(見圖1b中的加黑部位)上,施加分布力使葉片在離心力的作用下滿足力和力矩平衡條件。由于該葉片離心力近4.9×106N,在離心力作用下葉片背弧側、內弧側葉根圓角處部分區域的應力達到材料屈服極限,進入塑性區。

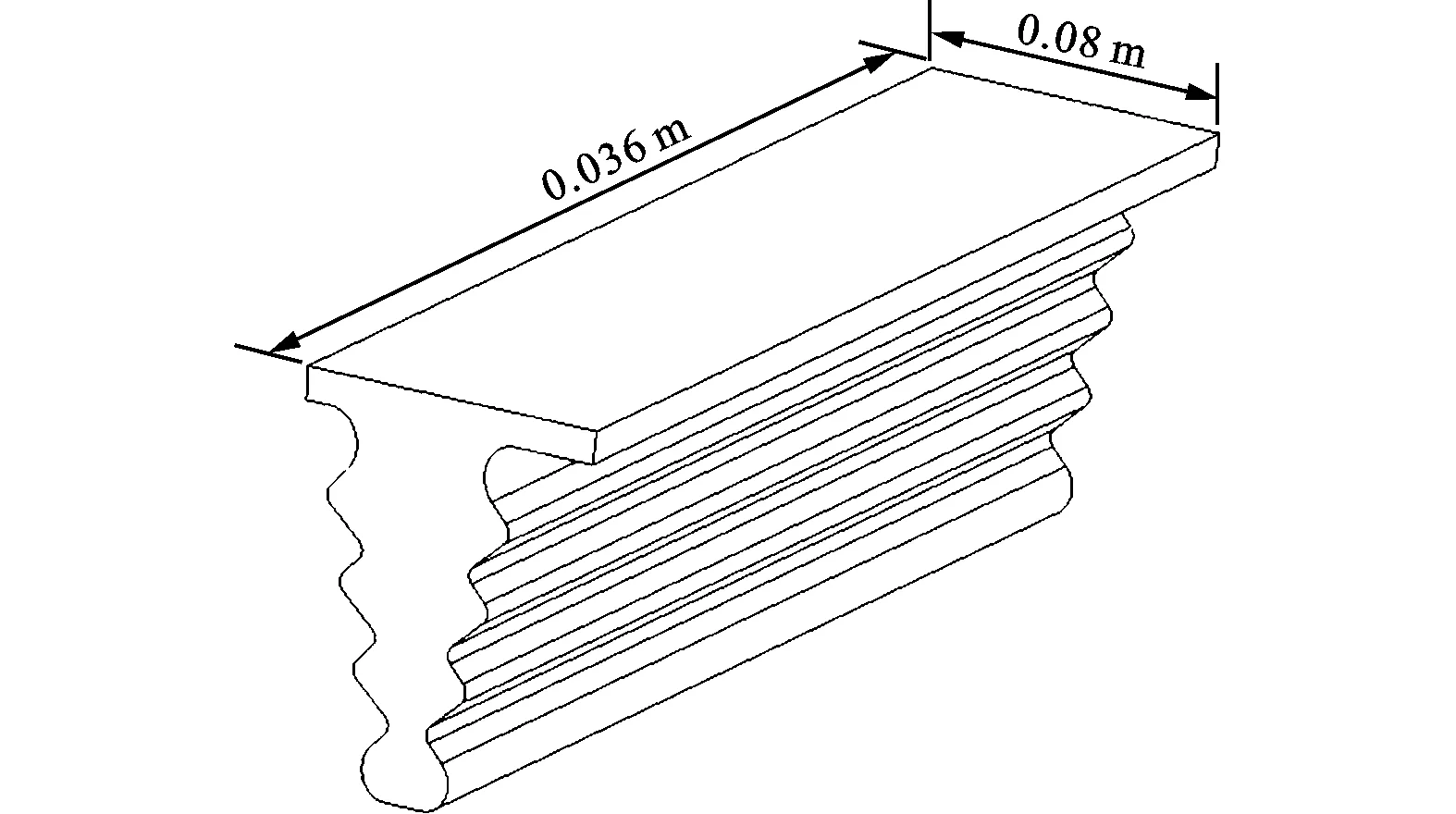
(a)三維實體

(b)有限元網格圖1 葉根三維實體及有限元網格

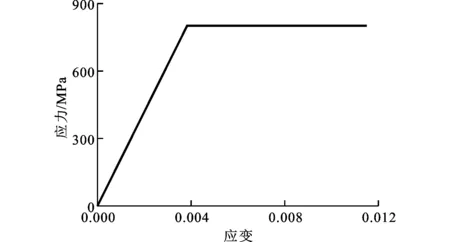
圖2 葉片材料應力-應變曲線

采用三維彈塑性有限元法計算了葉片的應力,葉片背弧側葉根圓角處應力沿軸向的分布見圖3。從圖3中可以看出,在彈性和塑性過渡的2個區域出現了2個類似“貓耳朵”的突起,其所表示的應力明顯大于理想彈塑性材料的屈服極限800 MPa,顯然是不合理的,即出現了應力奇異現象。

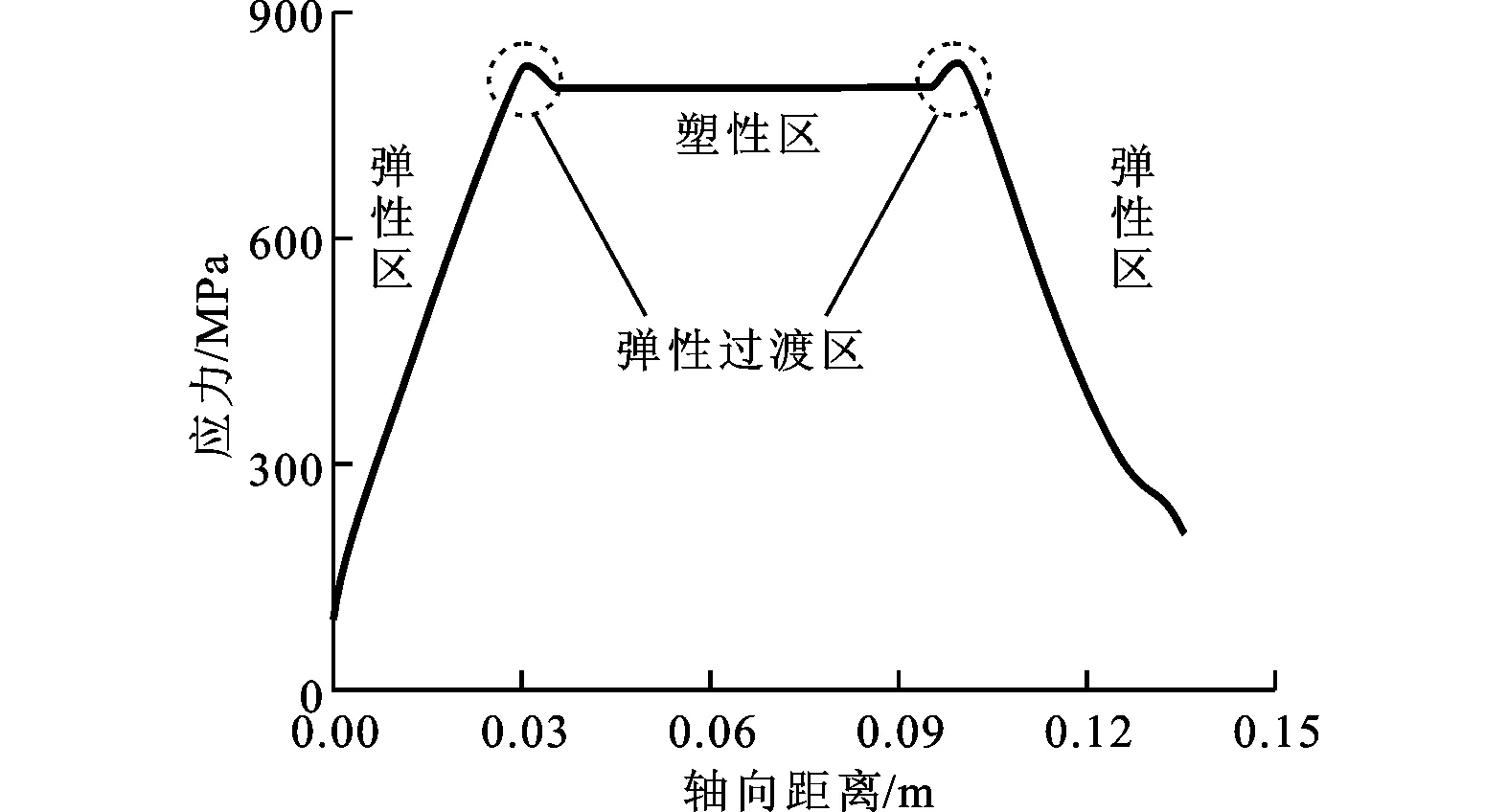
圖3 葉根圓角處應力沿軸向的分布

2 彈塑性過渡區應力奇異產生的原因

采用有限元法對葉片結構應力場進行分析時,通常先根據結構靜力平衡的有限元方程,計算得到葉片上所有單元節點的位移,然后基于位移場計算得到各單元高斯積分點上的應力,最后將高斯積分點的應力進行外推插值得到單元節點的應力[10]。本文將以六面體單元為例說明產生應力奇異的原因。

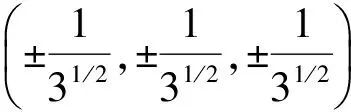
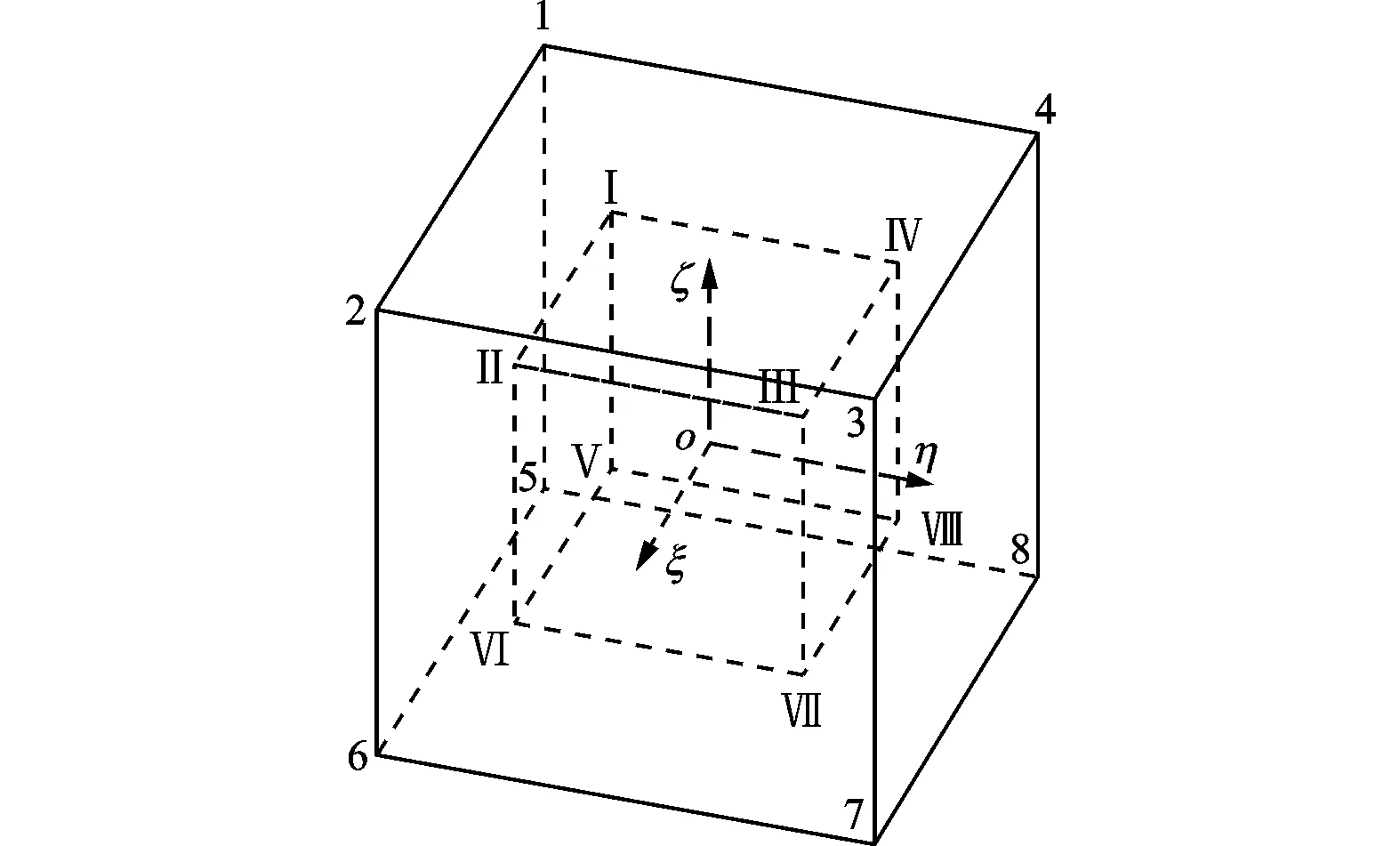
圖4 六面體單元及其高斯積分點示意

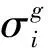
(1)

式中:Nij為形函數

(2)

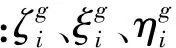
不失一般性,先設定一個簡單的應力場。該應力場包含塑性區和彈性區,并假設:彈性區與塑性區的交界面為平面;彈性區應力梯度大小(k=32 MPa)保持不變;塑性區為理想塑性,應力梯度為0,應力σs=800 MPa。那么,彈性區內任意一點P的應力

(3)

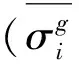
為方便分析,以彈性區應力梯度的方向由單元坐標系原點o指向單元節點1為例,研究了單元在應力場中的3種情況:單元整體位于彈性區;單元被彈塑性交界面分割成兩部分,一部分位于彈性區,另一部分位于塑性區;單元整體位于塑性區。

2.1 單元整體位于彈性區

單元整體位于彈性區時,根據單元與彈塑性交界面的距離可以分成多種情況。為方便分析,以節點1位于交界面上為例,比較節點的應力有限元值和實際應力值。

在應力場中,根據單元節點到彈塑性交界面的距離、采用式(3)可計算得到單元節點的實際應力,見表1。根據高斯積分點到彈塑性交界面的距離,先采用式(3)計算出高斯積分點的實際應力,然后將高斯積分點的應力代入到式(1)中,可計算得到單元節點應力的有限元計算值,見表1。

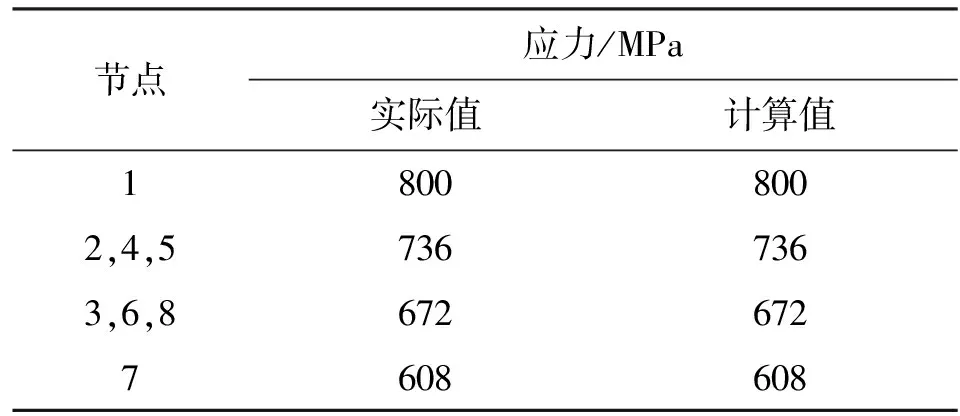
表1 位于彈性區時單元節點應力

從表1可以看出,單元各個節點應力的有限元計算值與單元節點的實際應力值相等,在此情況下單元節點應力沒有產生奇異現象。

2.2 單元跨過彈塑性交界面

單元一部分位于彈性區、另一部分位于塑性區,根據兩部分高斯積分點數及單元節點數又可以分成很多種情況。為了簡潔說明單元節點應力奇異的問題,結合式(3)、式(1)計算對以下4種情況進行分析。

(1)彈塑性交界面過高斯積分點Ⅰ。此時,只有單元節點1在塑性區,節點應力計算結果見表2。

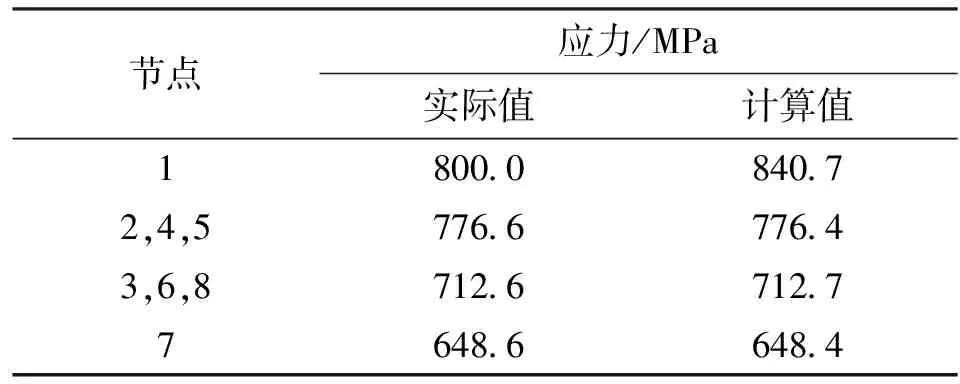
表2 交界面過高斯積分點I時單元節點應力

從表2可以看出,采用有限元插值公式計算出的單元節點1的應力超出了實際應力40.7 MPa,顯然是不合理的,即出現了應力奇異情況,這是由有限元節點應力的插值方式造成的。

(2)彈塑性交界面過高斯積分點Ⅱ、Ⅳ、Ⅴ。此時,單元節點1、2、4、5和高斯積分點Ⅰ在塑性區,單元高斯積分點Ⅱ、Ⅳ、Ⅴ在彈塑性交界面上,其余節點和高斯點在彈性區。節點應力計算結果見表3。

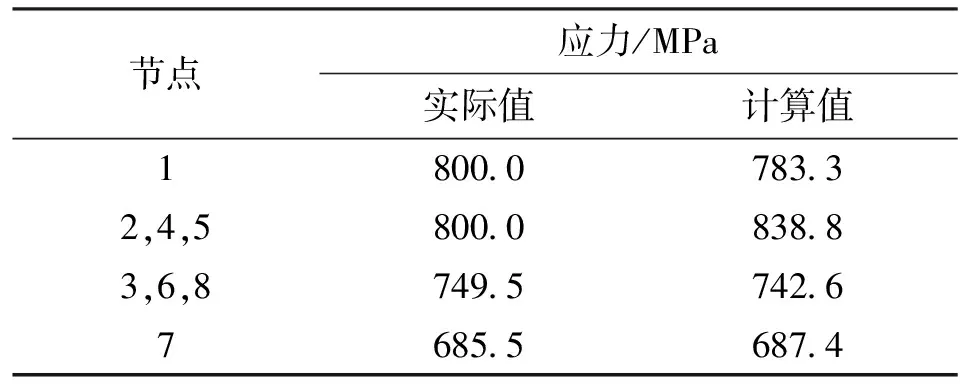
表3 交界面過高斯積分點Ⅱ、Ⅳ、Ⅴ時單元節點應力

從表3可以看出,節點1應力的有限元計算值比實際應力低16.7 MPa,單元節點2、4、5應力的有限元計算值超出實際應力38.8 MPa。這些計算結果是不合理的,即出現了應力奇異,這也是由有限元節點應力的插值方式造成的。

(3)彈塑性交界面過高斯積分點Ⅲ、Ⅵ、Ⅷ。此時,單元節點1、2、4、5和高斯積分點Ⅰ、Ⅱ、Ⅳ、Ⅴ在塑性區,高斯積分點Ⅲ、Ⅵ、Ⅷ在彈塑性交界面上,其余高斯積分點和節點在彈性區。節點應力計算結果見表4。

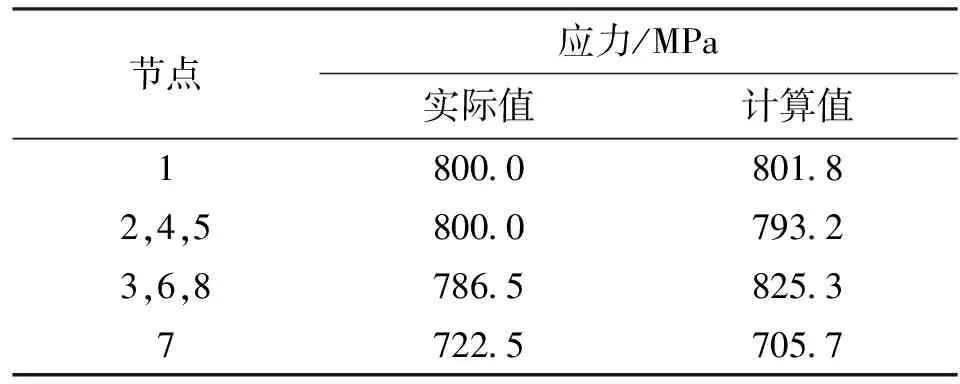
表4 交界面過高斯積分點Ⅲ、Ⅵ、Ⅷ時單元節點應力

從表4可以看出:單元節點2、4、5應力的有限元計算值比實際應力小6.8 MPa;單元節點3、6、8的應力有限元計算值超出實際應力38.8 MPa,應力奇異最為嚴重;單元節點7應力的有限元計算值比實際應力小16.8 MPa;單元節點1的應力沒有出現奇異。

(4)彈塑性交界面過高斯積分點Ⅶ。此時,只有單元節點7位于彈性區,所有高斯積分點和其余節點在塑性區。節點應力計算結果見表5。

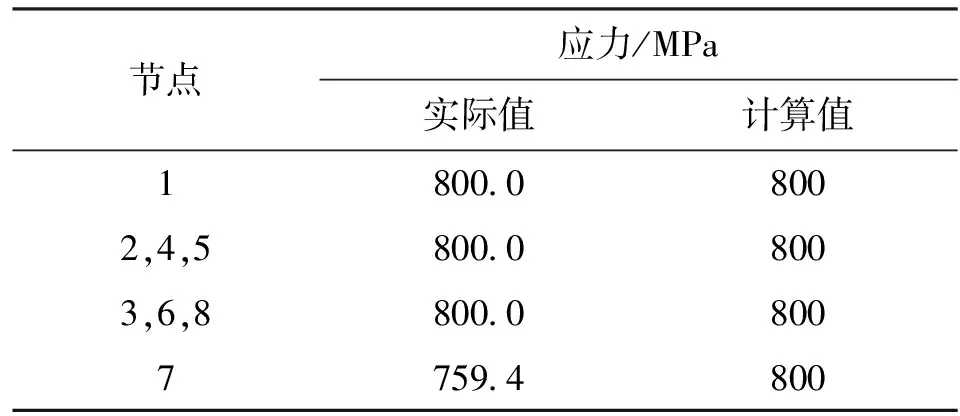
表5 交界面過高斯積分點Ⅶ時單元節點應力

從表5可以看出:單元節點7應力的有限元計算值超出實際應力40.6 MPa,產生應力奇異;其他節點應力沒有出現奇異。

2.3 單元整體位于塑性區

全部節點和高斯積分點都在塑性區。單元節點應力的有限元值和實際應力均等于屈服應力,單元節點應力沒有產生奇異。

綜上所述,單元整體處于彈性區或塑性區時,采用有限元法計算單元節點應力不會產生應力奇異現象。當單元跨過彈塑性交界面,即一部分處于彈性區域內、另一部分處于塑性區域內時,單元節點應力計算值會超出實際應力值,此時產生了應力奇異現象。分析認為,應力奇異是由有限元法計算單元節點應力時采用的外推插值算法造成的。

3 彈塑性過渡區應力奇異解決方法

在有限元方法中,不管是在彈性區和塑性區,還是在彈塑性過渡區,高斯積分點應力的有限元計算值都不會產生奇異。采用單元節點附近不同單元內的高斯積分點應力的加權平均值作為單元節點的應力,可以消除單元節點應力奇異現象。加權平均方法計算單元節點應力的計算式為

(4)

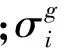
以六面體單元的高斯積分點I位于彈塑性交界面上為例,采用有限元節點應力公式計算得到節點1的應力為840.7 MPa,超出節點實際應力800 MPa,即產生了應力奇異。根據高斯積分點到彈塑性交界面的距離,采用式(3)計算出節點1附近高斯積分點的應力,然后將各個高斯積分點應力代入到式(4)中,計算出節點1的應力為800 MPa,與節點1的實際應力800 MPa一致,即節點1應力的計算值沒有發生奇異。

以圖1中所示的葉根為例對葉片進行應力分析,得到葉片根部圓角處應力的分布曲線,見圖5。從圖5可以看出,在葉片根部彈塑性過渡區,采用加權平均方法計算出的應力未出現奇異現象。因此,對葉片進行彈塑性有限元分析時節點應力可采用與節點相鄰的高斯積分點應力的加權平均進行計算。

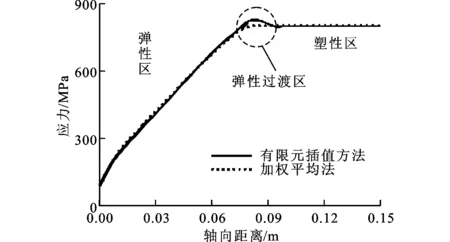
圖5 采用加權平均方法得到的應力沿軸向的分布

4 結 論

本文基于理想彈塑性模型,對葉片有限元分析中根部彈塑性過渡區應力奇異的問題進行了研究。研究表明,當單元一部分位于彈性區、另一部分位于塑性區時,有限元節點應力的外插算法會造成節點應力計算值高于結構的實際應力,甚至超出理想彈塑性材料的屈服極限,使應力產生奇異。研究也發現,在葉片有限元分析中,采用節點相鄰的高斯積分點應力的加權平均方法計算節點應力,能有效避免葉片彈塑性過渡區的應力奇異現象。該研究可為大型汽輪機、重型燃機及航空發動機葉片強度設計提供參考。

[1] 王為民, 潘家成. 東方-日立型超超臨界1 000 MW汽輪機可靠性設計 [J]. 熱力透平, 2006, 35(1): 8-12. WANG Weimi, PAN Jiacheng. Reliability of ultra-supercritical 1 000 MW steam turbine designed by DFSTW and Hitachi [J]. Thermal Turbine, 2006, 35(1): 8-12.

[2] HISASHI F, HIROHARU O, TOSHIHIRO M, et al. Development of 3,600-rpm 50-inch/3,000-rpm 60-inch ultra-long exhaust end blades [J]. Mitsubishi Heavy Industries Technical Review, 2009, 46(2): 18-25.

[3] RAO J S, SURESH S. Blade root shape optimization [J]. Proceedings of Future of Gas Turbine Technology, 2006, 13(2): 1-11.

[4] 徐自力, 李辛毅, 安寧, 等. 相關參數對汽輪機低壓葉片疲勞壽命的影響 [J]. 動力工程, 2004, 24(1): 33-36. XU Zili, LI Xinyi, AN Ning, et al. Effect of relative factors on fatigue life for low pressure blades of steam turbines [J]. Power Engineering, 2004, 24(1): 33-36.

[5] SINCLAIR G B, CORMIER N G, GRIFFIN J H, et al. Contact stresses in dovetail attachments: finite element modeling [J]. ASME Journal of Engineering for Gas Turbines and Power, 2002, 124: 182-189.

[6] SINCLAIR G B, CORMIER N G. Contact stresses in dovetail attachments: alleviation via precision crowning [J]. ASME Journal of Engineering for Gas Turbines and Power, 2003, 125: 1033-1041.

[7] 李彬, 宋立明, 李軍, 等. 長葉片透平級多學科多目標優化設計 [J]. 西安交通大學學報, 2014, 48(1): 1-5. LI Bin, SONG Liming, LI Jun, et al. Multidisciplinary and multi objective optimization design of long blade turbine stage [J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 1-5.

[8] RAO J S, KISHORE C B, MAHADEVAPPA V. Weight optimization of turbine blades [C]∥Proceedings of the 12th International Symposium on Transport Phenomena and Dynamics of Rotating Machinery. Honolulu, Hawaii, USA: Altair Engineering Inc., 2008: 1-19.

[10]ZIENKIEWICZ O C, TAYLOR R L, ZHU J Z. The finite element method: its basis and fundamentals [M]. 6th Edition. Oxford, UK: Butterworth-Heinemann, 2005: 462-467.

[11]COOK R D, MALKUS D S, PLESHA M E, et al. Concepts and applications of finite element analysis [M]. 4th ed. New York, USA: Wiley, 2001: 198-200.

(編輯 苗凌)

(1.西安交通大學航天航空學院,710049,西安;2.西安交通大學機械結構強度與振動國家重點實驗室,710049,西安;3.東方汽輪機有限公司,618000,四川德陽)

采用彈塑性有限元法、借助大型商業有限元軟件對汽輪機葉片進行應力分析時,彈塑性過渡區應力的計算值有時會高于塑性區應力的計算值,即會產生應力奇異現象。為分析產生這一現象的原因,以8節點六面體單元為例,研究了有限元法計算應力的過程,并在理想彈塑性的條件下,采用有限元法和解析法計算了彈塑性過渡區單元節點應力。研究發現,有限元法通常采用高斯積分點應力值外推插值法得到單元節點應力,當單元一部分位于彈性區、另一部分位于塑性區時,這種外插算法會導致節點應力計算值高于結構的實際應力,甚至超出理想彈塑性材料的屈服極限,從而造成應力奇異。研究表明,在葉片彈塑性的有限元分析中,采用相鄰高斯積分點應力加權平均的方法計算單元節點應力,可有效避免彈塑性過渡區應力產生奇異的現象。

葉片;有限元;彈塑性過渡區;應力奇異

Origin and Elimination of Stress Singularity in Blade Elasto-Plastic Transition Region in Finite Element Analysis

ZHONG Jize1,2,XU Zili1,2,FANG Yu3,FAN Xiaoping3,ZHAO Shiquan3

(1. School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China; 2. State Key Laboratory for Strength and Vibration of Mechanical Structures, Xi’an Jiaotong University, Xi’an 710049, China; 3. Dongfang Turbine Co., Ltd., Deyang, Sichuan 618000, China)

When stresses of steam turbine blades are computed with the finite element method, sometimes the calculated stress in elasto-plastic transition region gets higher than the calculated stress in plastic region, namely there exits stress singularity. To explain this fact, the calculation process of nodal stress with finite element method is discussed in detail, where a kind of 8-node hexahedron element and an ideal elasto-plastic material model are chosen as the example. Nodal stresses of the elements in elasto-plastic transition region are comparatively calculated. It is found that in the finite element method the nodal stress is calculated via extrapolation of stresses at Gauss integration point in an element, and the calculated nodal stress maybe exceed the actual stress even the yield limit of ideal elasto-plastic material when one part of an element is located in elastic zone and the other part remains in plastic zone, thus stress singularity is brought out by the extrapolation algorithm. It is suggested that the nodal stresses are calculated in terms of weighted average stress at Gauss integration points of neighboring elements to effectively eliminate stress singularity.

blade; finite element method; elastic-plastic transition region; stress singularity

2014-12-17。 作者簡介:仲繼澤(1988—),男,博士生;徐自力(通信作者),男,教授,博士生導師。 基金項目:國家“973計劃”資助項目(2011CB706505);國家自然科學基金資助項目(51275385)。

時間:2015-06-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20150617.0902.010.html

10.7652/xjtuxb201509009

TK263.3;TB125

A

0253-987X(2015)09-0047-05