新型磁鏈觀測算法及其在永磁同步電機無位置傳感器控制中的應(yīng)用

李彪,李黎川

(西安交通大學電氣工程學院,710049,西安)

?

新型磁鏈觀測算法及其在永磁同步電機無位置傳感器控制中的應(yīng)用

李彪,李黎川

(西安交通大學電氣工程學院,710049,西安)

針對傳統(tǒng)電壓型磁鏈觀測器在對電機內(nèi)普遍存在的橢圓形磁場磁鏈進行觀測時存在穩(wěn)態(tài)幅值相位誤差的問題,依據(jù)穩(wěn)態(tài)時磁鏈與感應(yīng)電動勢在時域的基本關(guān)系,提出了2種結(jié)構(gòu)簡單、易于工程實現(xiàn)的新型磁鏈觀測算法。新算法在同步角頻率處與純積分具有相同的頻率特性,α、β兩相磁鏈觀測不存在耦合,不再需要兩相對稱或感應(yīng)電動勢矢量與磁鏈矢量正交,因此能夠?qū)A形和橢圓形磁鏈進行準確觀測。對新算法進行了仿真,結(jié)果表明:新算法有效地消除了積分漂移,不存在穩(wěn)態(tài)誤差。將新算法應(yīng)用于一臺表貼式永磁同步電機無位置傳感器調(diào)速系統(tǒng)的轉(zhuǎn)子位置估算,并利用數(shù)字信號處理器TMS320F2812DSP對算法進行了數(shù)字化實現(xiàn),結(jié)果表明:新算法在10%額定轉(zhuǎn)速以上時具有良好的轉(zhuǎn)速和位置跟蹤效果,但在低速區(qū)估算結(jié)果不穩(wěn)定;新算法具有良好的幅值、相位觀測精度,從而使系統(tǒng)具有良好的穩(wěn)態(tài)特性;當電機轉(zhuǎn)速突變時,新算法具有良好的磁鏈觀測精度,從而使系統(tǒng)具有良好的動態(tài)特性。

磁鏈觀測器;橢圓形旋轉(zhuǎn)磁場;永磁同步電動機;無位置傳感器控制

準確的磁鏈觀測是實現(xiàn)交流電機磁場定向控制和直接轉(zhuǎn)矩控制的關(guān)鍵。電壓型磁鏈觀測器由于算法簡單,易于實現(xiàn),對參數(shù)依賴小(僅需要電機定子電阻參數(shù)),從而在工業(yè)中獲得了廣泛的應(yīng)用。但是,電壓型磁鏈觀測器中的純積分環(huán)節(jié)會在觀測的磁鏈中引入初始相位誤差和直流偏置誤差,產(chǎn)生積分漂移,從而引起轉(zhuǎn)矩脈動,影響系統(tǒng)運行的穩(wěn)定性。為了解決此純積分存在的問題,常用一階低通濾波器(LPF)來代替純積分,從而消除初始相位誤差并抑制直流偏置誤差,但是在穩(wěn)態(tài)時,尤其是當電機運行在低通濾波器截止頻率以下時,又會存在幅值相位誤差。文獻[1]提出根據(jù)電機轉(zhuǎn)速動態(tài)調(diào)整濾波器的截止頻率來降低低速時觀測磁鏈的穩(wěn)態(tài)幅值相位誤差,但是隨著電機轉(zhuǎn)速降低,算法中低通濾波器的截止頻率也隨之降低,大的時間常數(shù)導(dǎo)致在輸入變化時觀測結(jié)果又存在漂移問題。文獻[2-7]采用一階低通濾波器代替純積分,用一個補償環(huán)節(jié)來補償穩(wěn)態(tài)幅值相位誤差。文獻[5,8]指出,交換低通濾波環(huán)節(jié)與補償環(huán)節(jié)的相對位置,可以增強磁鏈觀測器動態(tài)時的觀測精度。文獻[9]采用一階高通濾波器(HPF)代替純積分,用一個坐標變換環(huán)節(jié)補償穩(wěn)態(tài)幅值相位誤差。文獻[10-13]采用一階低通濾波器與一階高通濾波器串聯(lián)代替純積分,再串聯(lián)補償環(huán)節(jié)來補償穩(wěn)態(tài)幅值相位誤差。文獻[14]采用帶通濾波器(BPF)代替純積分環(huán)節(jié),并對觀測磁鏈的穩(wěn)態(tài)幅值相位誤差進行補償。文獻[15]中的算法采用五階低通濾波器串聯(lián)一階高通濾波器和一個邏輯轉(zhuǎn)換模塊,消除了積分漂移,同時抑制了系統(tǒng)中的高頻干擾。

關(guān)于濾波器截止頻率的選取,文獻[4-6,9-12,15]中的可編程濾波器采用的截止頻率是同步角頻率的某一倍數(shù),而不是取某一固定值,從而使算法在低速時兼顧了對直流偏置的抑制能力與動態(tài)過程中磁鏈觀測的精度。關(guān)于穩(wěn)態(tài)時幅值與相位誤差的補償,文獻[3-7,12,14]中的補償環(huán)節(jié)采用了旋轉(zhuǎn)空間矢量的方法,文獻[2,8,10-11,13,15]中的補償環(huán)節(jié)通過分析相關(guān)時間相量之間的關(guān)系得到,而文獻[9]則采用坐標變換實現(xiàn)補償。文獻[7]還引入定子磁鏈的電流模型和電壓模型之間的誤差對定子感應(yīng)電動勢進行補償。文獻[16]采用低通濾波器代替純積分,并用另一個低通濾波器進行幅值相位補償,但2個低通濾波器的截止頻率要求嚴格,需滿足一定關(guān)系,且在低速時無法使2個濾波器的時間常數(shù)同時較低。文獻[17-18]采用低通濾波器代替純積分,用經(jīng)過低通濾波的磁鏈反饋補償穩(wěn)態(tài)時的幅值相位誤差,通過檢測感應(yīng)電動勢矢量和磁鏈矢量的正交程度來決定反饋補償程度。

對文獻[2-15,17-18]]中的算法進行分析后發(fā)現(xiàn),在穩(wěn)態(tài)時觀測磁鏈的準確性必須基于以下條件之一:

(1)在時域,α、β兩相對稱;

(2)在空間,感應(yīng)電動勢矢量與磁鏈矢量的幅值之比等于同步角頻率,磁鏈矢量滯后于感應(yīng)電動勢矢量90°(電機反轉(zhuǎn)時則超前90°)。

分析可知這2個條件等價,且只在圓形磁場時成立。

一般情況下,電機本體設(shè)計和實時控制都期望電機中的磁場呈圓形,而在實際中,由于電機電阻、電感參數(shù)的不對稱,逆變器電壓-電流的非線性特性,逆變器開關(guān)量所加死區(qū)的影響,各相電流檢測電路及調(diào)理電路的不對稱,AD采樣轉(zhuǎn)換電路的不對稱,負載不對稱等各種因素的影響,以及在調(diào)速系統(tǒng)動態(tài)調(diào)整過程中,電機磁場都會呈橢圓形。

當電機磁場呈橢圓形時,通過分析可知前述算法不再有效,從而出現(xiàn)磁鏈觀測穩(wěn)態(tài)誤差。圖1所示為α、β兩相感應(yīng)電動勢存在5%幅值誤差和10%相位誤差時(具體參數(shù)見本文仿真部分),傳統(tǒng)典型算法的穩(wěn)態(tài)觀測結(jié)果。本文依據(jù)穩(wěn)態(tài)時磁鏈相量與感應(yīng)電動勢相量的基本關(guān)系,提出2種新的算法。新算法在同步角頻率處與純積分具有相同的頻率特性,α、β兩相磁鏈觀測不存在耦合,不再需要兩相對稱或感應(yīng)電動勢矢量與磁鏈矢量正交,因此對圓形橢圓形磁鏈均能夠進行準確觀測。將新算法用于永磁同步電機無位置傳感器調(diào)速系統(tǒng)的轉(zhuǎn)子位置估算,通過仿真與實驗證明了新算法的正確性和實用性。

(a) 文獻[14]算法的觀測結(jié)果 (b) 文獻[15]算法的觀測結(jié)果圖1 傳統(tǒng)磁鏈觀測算法對橢圓形磁鏈的觀測結(jié)果

1 新算法的原理

在靜止兩相α-β坐標系下,交流電機電壓模型的磁鏈表達式為

(1)

式中:Ψα,β、eα,β、vα,β、iα,β分別為磁鏈、感應(yīng)電動勢、端電壓與電流的α、β軸分量;R為繞組電阻。

1.1 穩(wěn)態(tài)時磁鏈與感應(yīng)電動勢的關(guān)系

穩(wěn)態(tài)時感應(yīng)電動勢相量與磁鏈相量的關(guān)系為

(2)

式中:ωe為同步角頻率。無論圓形磁場或橢圓形磁場,式(2)所示相量關(guān)系均成立。因此,本文將式(2)作為基本關(guān)系,在此基礎(chǔ)上提出新的磁鏈觀測算法。

1.2 新磁鏈觀測算法

1.2.1 算法1 初始相位誤差和直流偏置誤差作為直流量存在于純積分觀測磁鏈時的輸出中,引起漂移。因此,在純積分輸出端串聯(lián)一個帶通濾波器,利用其原點處的零點使帶通濾波器對直流量增益為零,以解決漂移問題,再通過輸出負反饋以補償串聯(lián)帶通濾波器后引入的穩(wěn)態(tài)幅值相位誤差。算法1的原理框圖如圖2所示,其中b為待定反饋系數(shù),ωe為同步角頻率,GBPF為帶通濾波器的傳遞函數(shù)

(3)

式中:ωn為帶通濾波器的中心頻率,ωn=kωe;ξ為阻尼系數(shù)。

圖2 算法1的原理框圖

算法1采用中心頻率為同步角頻率k倍的可編程帶通濾波器,k值的選取會影響系統(tǒng)的動、靜態(tài)性能。

由圖2可得算法1的傳遞函數(shù)為

(4)

為消除穩(wěn)態(tài)時的幅值相位誤差,通過選取適當?shù)姆答佅禂?shù)b,使算法的傳遞函數(shù)在同步角頻率處與積分具有相同的頻率特性,即

(5)

由式(4)、式(5)可得反饋系數(shù)

(6)

1.2.2 算法2 算法1中利用帶通濾波器在原點處的零點對消掉積分在原點處的極點,因此可以消除初始相位誤差,但對直流偏置誤差卻只能抑制而無法徹底消除。要徹底消除直流偏置誤差,則算法需要有一個原點處的零點。

在相量平面,任一相量都可以通過2個方向不同的非零相量的線性運算得到。依據(jù)磁鏈相量與感應(yīng)電動勢相量的關(guān)系,算法2的原理如圖3a所示:先讓感應(yīng)電動勢經(jīng)過一個帶通濾波器以徹底消除積分漂移,同時濾除系統(tǒng)高頻干擾,帶通濾波器中心頻率選擇等于同步角頻率,這樣對感應(yīng)電動勢的基波幅值與相位均無影響;然后,再利用濾波后的感應(yīng)電動勢相量和感應(yīng)電動勢經(jīng)過一移相網(wǎng)絡(luò)后得到的相量進行線性運算,得到磁鏈相量。各相量之間的關(guān)系如圖3b所示。

(a)算法2原理示意圖

(b)相量關(guān)系圖圖3 算法2的原理框圖

算法2中帶通濾波器的傳遞函數(shù)為

(7)

式中:B為帶寬,B=2ξωe。

假設(shè)選取的移相網(wǎng)絡(luò)在同步角頻率ωe處的頻率特性為F∠-θ,則有

(8)

(9)

式中:k1、k2為線性運算系數(shù)。通過解三角形可得

(10)

(11)

算法2在仿真與實驗中選擇的移相網(wǎng)絡(luò)傳遞函數(shù)為

(12)

則有:F=1;k1=-k/ωe;k2=(1+k2)1/2/ωe。

新磁鏈觀測算法中α、β兩相不存在耦合,不要求兩相對稱,因此對圓形和橢圓形磁鏈均可以進行準確觀測。

2 仿 真

為了驗證新算法的有效性,在Matlab/Simulink中進行離散系統(tǒng)仿真,采樣頻率為12 kHz。算法1取k=0.4,ξ=0.5;算法2取k=1.2,ξ=0.5。

圖4a所示為仿真所加感應(yīng)電動勢:在0～0.25 s,感應(yīng)電動勢幅值為7.97 V,頻率為20 Hz;在0.25 s,感應(yīng)電動勢幅值躍變?yōu)?5.94 V,頻率躍變?yōu)?0 Hz;在0～0.5 s,感應(yīng)電動勢均疊加了大小為幅值1%的直流偏置。圖4b所示為純積分法的磁鏈觀測結(jié)果,可見存在明顯的初始相位誤差與直流偏置誤差。圖4c所示為算法1的磁鏈觀測結(jié)果,圖4d所示為算法2的磁鏈觀測結(jié)果,從中可以看出,新算法有效地消除了積分漂移,不存在穩(wěn)態(tài)誤差。

(a)感應(yīng)電動勢

(b)純積分法的觀測結(jié)果

(c)算法1的觀測結(jié)果

(d)算法2的觀測結(jié)果圖4 新磁鏈觀測算法與純積分法的磁鏈觀測結(jié)果比較

圖5所示為兩相感應(yīng)電動勢不對稱、磁鏈軌跡為橢圓形時,新磁鏈觀測算法的穩(wěn)態(tài)觀測結(jié)果。所加感應(yīng)電動勢頻率為20 Hz,α相幅值為7.97 V,β相幅值為α相的0.95倍,β相感應(yīng)電動勢的相位滯后于α相9π/20,同時兩相感應(yīng)電動勢均疊加了大小為各自幅值1%的直流偏置。仿真結(jié)果證明,新算法可以對橢圓形磁鏈進行準確觀測。文獻[14-15]中算法的觀測結(jié)果如圖1所示,由于這2種算法是基于圓形磁場的,因此對于橢圓形磁鏈的觀測結(jié)果存在穩(wěn)態(tài)誤差。

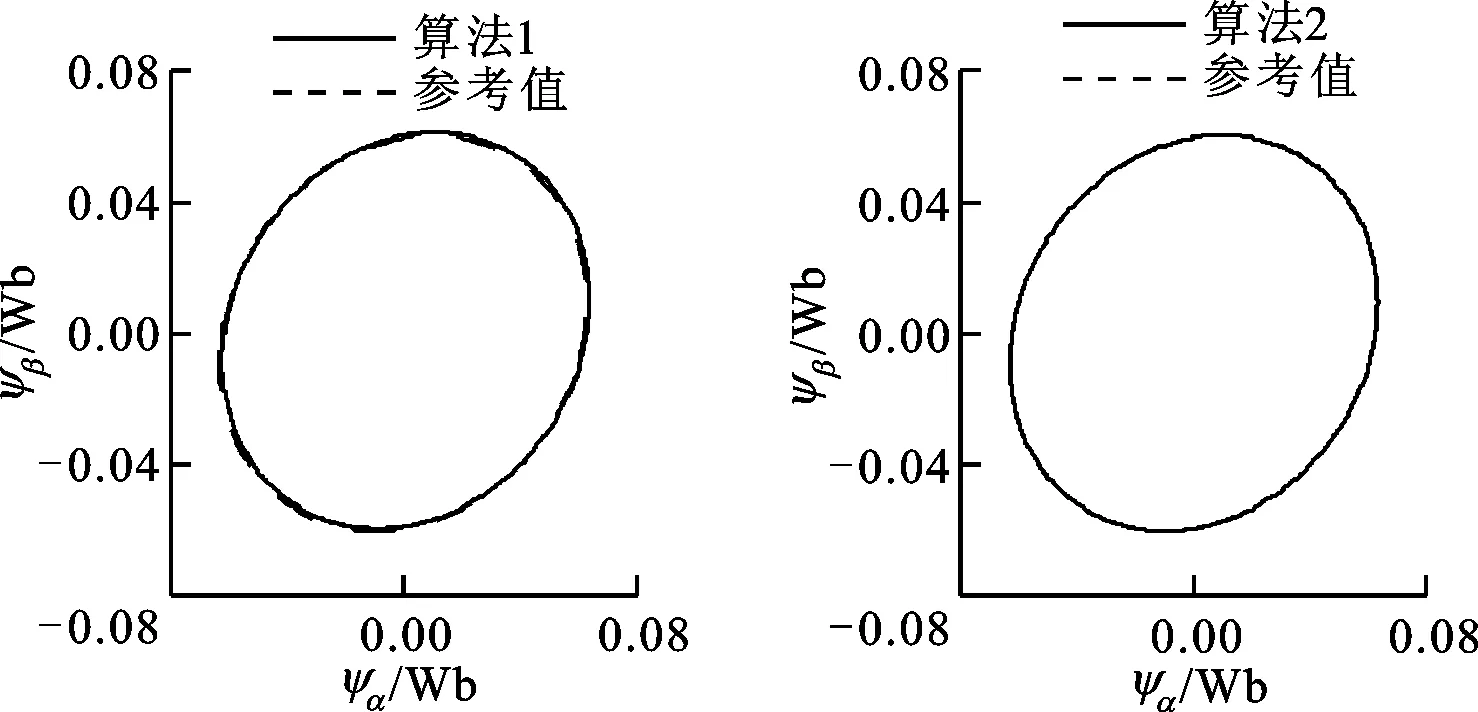
(a)算法1的觀測結(jié)果(b)算法2的觀測結(jié)果圖5 新磁鏈觀測算法對橢圓形磁鏈的觀測結(jié)果

3 實驗研究

將本文的新磁鏈觀測算法應(yīng)用于一臺表貼式永磁同步電機無位置傳感器調(diào)速系統(tǒng)的轉(zhuǎn)子位置估算,系統(tǒng)控制框圖如圖6所示。系統(tǒng)采用速度-電流雙閉環(huán)矢量控制,電流環(huán)采用id=0控制策略。電機繞組電流采用霍爾傳感器實時檢測。系統(tǒng)控制周期,電流采樣及調(diào)節(jié)周期,磁鏈、位置與速度的估算周期均取83.3μs;速度環(huán)調(diào)節(jié)周期為10Ts(Ts為系統(tǒng)控制周期),為抗積分飽和,速度環(huán)采用積分分離的PI調(diào)節(jié)器。實驗平臺實物圖如圖7所示,逆變器主電路由MOSFET構(gòu)成,主控芯片采用TI公司的TMS320F2812型數(shù)字信號處理器,片內(nèi)集成有A/D轉(zhuǎn)換模塊。實驗電機參數(shù):額定功率為0.4kW;額定電壓為106V;額定電流為2.5A;額定轉(zhuǎn)速為3 000r/min;交、直軸電感為5.55mH;定子電阻為1.4Ω;極對數(shù)為4;永磁體磁鏈為0.063 419 7Wb。

調(diào)速系統(tǒng)采用磁鏈法估算轉(zhuǎn)子的位置

(13)

(14)

式中:p為極對數(shù)。

圖6 永磁同步電機無位置傳感器控制系統(tǒng)框圖

(a)控制器部分 (b)電機部分圖7 實驗平臺實物圖

新磁鏈觀測算法中需要的同步角頻率從感應(yīng)電動勢信號中提取。當磁鏈軌跡為圓形或近似橢圓形時,同步角頻率就等于感應(yīng)電動勢矢量在空間的旋轉(zhuǎn)角速度,可通過下式計算

(15)

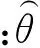
(16)

上述方法雖然簡單、易實現(xiàn),但當電機磁場的橢圓度較大時,得到的感應(yīng)電動勢矢量空間旋轉(zhuǎn)角速度并不等于同步角頻率。此時,橢圓形旋轉(zhuǎn)感應(yīng)電動勢矢量可以分解為2個轉(zhuǎn)速相等、轉(zhuǎn)向相反的圓形旋轉(zhuǎn)分量,同步角頻率就等于其中正向旋轉(zhuǎn)分量的空間旋轉(zhuǎn)角速度。正向旋轉(zhuǎn)分量在時域?qū)?yīng)的是感應(yīng)電動勢相量的正序分量,可以由式(17)、式(18)計算得到

(17)

(18)

式中:jeα、jeβ屬于算法2中計算磁鏈過程的中間變量,如圖8所示。

圖8 算法2計算磁鏈的原理框圖

對感應(yīng)電動勢的正序分量進行低通濾波后,代入式(19)得到感應(yīng)電動勢矢量正向旋轉(zhuǎn)分量的空間角度,再經(jīng)過式(20)估算同步角頻率。

(19)

(20)

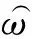
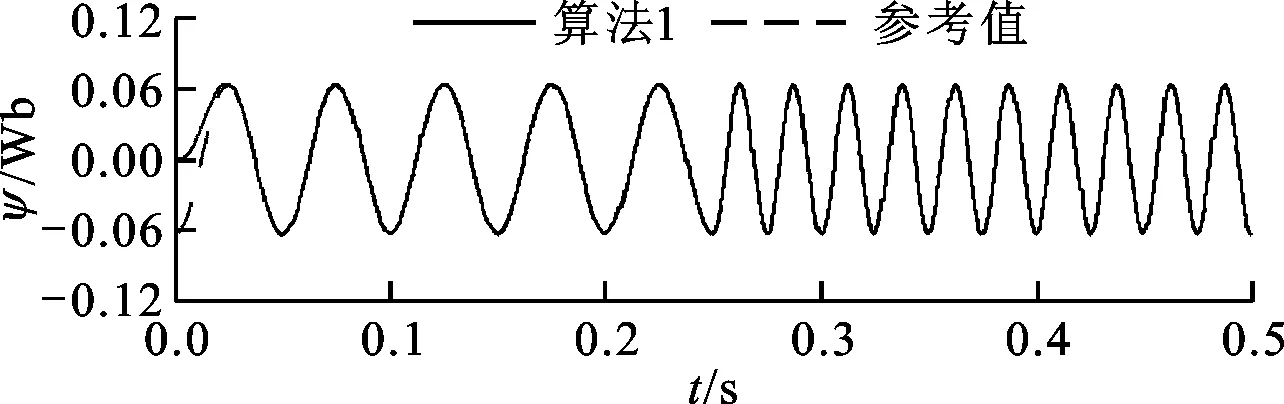
(a)算法1的磁鏈觀測結(jié)果 (b)算法2的磁鏈觀測結(jié)果圖9 參考轉(zhuǎn)速為450 r/min時的感應(yīng)電動勢波形與 新磁鏈觀測算法觀測的磁鏈波形

(a)轉(zhuǎn)速躍變時算法1的磁鏈觀測結(jié)果

(b)轉(zhuǎn)速躍變時算法2的磁鏈觀測結(jié)果圖10 參考轉(zhuǎn)速在450至1 000 r/min之間躍變時的 電機轉(zhuǎn)速估算波形與新算法觀測的磁鏈波形

圖10為當電機參考轉(zhuǎn)速在450至1 000 r/min之間躍變時,電機轉(zhuǎn)速的估算值與新磁鏈觀測算法觀測的定子磁鏈波形。由圖可見,當電機轉(zhuǎn)速躍變時,新算法均具有良好的磁鏈觀測精度,從而使系統(tǒng)具有良好的動態(tài)特性。

圖11為電機參考轉(zhuǎn)速在450至1 000 r/min之間躍變時,電機轉(zhuǎn)速估算波形與新磁鏈觀測算法估算的電機轉(zhuǎn)子位置角波形。

(a)轉(zhuǎn)速躍變時算法1的轉(zhuǎn)子位置角估算結(jié)果

(b)轉(zhuǎn)速躍變時算法2的轉(zhuǎn)子位置角估算結(jié)果圖11 參考轉(zhuǎn)速在450至1 000 r/min之間躍變時的 電機轉(zhuǎn)速估算波形與新磁鏈觀測算法估算的 轉(zhuǎn)子位置角波形

4 結(jié) 論

(1)電壓型磁鏈觀測器中的純積分存在漂移問題。傳統(tǒng)磁鏈觀測算法的推導(dǎo)要求α、β兩相對稱,或要求磁鏈矢量與感應(yīng)電動勢矢量正交,這雖然可以解決漂移問題,但算法僅對圓形磁場是準確的,而對實際中更普遍存在的橢圓形磁場,進行觀測時則存在穩(wěn)態(tài)誤差。

(2)本文提出的2種新磁鏈觀測算法不需要α、β兩相對稱或磁鏈矢量與感應(yīng)電動勢矢量空間正交,因此對圓形與橢圓形磁鏈均可以進行準確觀測。算法1具有簡單的優(yōu)點,適用于低成本應(yīng)用場合;算法2的計算量相對稍大,但是可以完全消除積分漂移,并且實驗證明算法2具有更好的動、靜態(tài)性能。

(3)新算法編程實現(xiàn)簡單,可以應(yīng)用于工業(yè)的實時控制系統(tǒng)。將新算法應(yīng)用于永磁同步電機無位置傳感器調(diào)速系統(tǒng)中的轉(zhuǎn)子位置估算,系統(tǒng)運行穩(wěn)定可靠,證明了算法的實用性。

[1] 張旭, 瞿文龍. 一種低速下磁鏈觀測補償?shù)男路椒?[J]. 電工電能新技術(shù), 2003, 22(3): 50-54. ZHANG Xu, QU Wenlong. A novel compensation method of stator flux estimating in low speed region [J]. Advanced Technology of Electrical Engineering and Energy, 2003, 22(3): 50-54.

[2] NIK I N R, MOHAMED Y A H. An improved stator flux estimation in steady-state operation for direct torque control of induction machines [J]. IEEE Transactions on Industry Applications, 2002, 38(1): 110-116.

[3] LI Yong, HUANG Wenxin, HU Yuwen. A low cost implementation of stator-flux-oriented induction motor drive [C]∥Proceedings of the Eighth International Conference on Electrical Machines and Systems. Piscataway, NJ, USA: IEEE, 2005: 1534-1538.

[4] SHIN M H, HYUN D S, CHO S B, et al. An improved stator flux estimation for speed sensorless stator flux orientation control of induction motors [J]. IEEE Transactions on Power Electronics, 2000, 15(2): 312-318.

[5] HINKKANEN M, LUOMI J. Modified integrator for voltage model flux estimation of induction motors [J]. IEEE Transactions on Industrial Electronics, 2003, 50(4): 818-820.

[6] COMANESCU M L, XU L. An improved flux observer based on PLL frequency estimator for sensorless vector control of induction motors [J]. IEEE Transactions on Industrial Electronics, 2006, 53(1): 50-56.

[7] 陳振鋒, 鐘彥儒, 李潔, 等. 基于改進磁鏈觀測器的感應(yīng)電機轉(zhuǎn)速辨識 [J]. 電工技術(shù)學報, 2012, 27(4): 42-47. CHEN Zhenfeng, ZHONG Yanru, LI Jie, et al. Speed identification for induction motor based on improved flux observer [J]. Transactions of China Electrotechnical Society, 2012, 27(4): 42-47.

[8] 何志明, 廖勇, 何大為. 定子磁鏈觀測器低通濾波器的改進 [J]. 中國電機工程學報, 2008, 28(18): 61-65. HE Zhiming, LIAO Yong, HE Dawei. Improvement of low-pass filter algorithm for stator flux estimator [J]. Proceedings of the CSEE, 2008, 28(18): 61-65.

[9] 王宇, 鄧智泉, 王曉琳. 一種新穎的電機磁鏈辨識算法 [J]. 中國電機工程學報, 2007, 27(6): 39-44. WANG Yu, DENG Zhiquan, WANG Xiaolin. A novel algorithm of motor flux estimation [J]. Proceedings of the CSEE, 2007, 27(6): 39-44.

[10]張星, 瞿文龍, 陸海峰. 一種能消除直流偏置和穩(wěn)態(tài)誤差的電壓型磁鏈觀測器 [J]. 電工電能新技術(shù), 2006, 25(1): 39-43. ZHANG Xing, QU Wenlong, LU Haifeng. Method for elimination of DC offset and steady state error for voltage module flux observer [J]. Advanced Technology of Electrical Engineering and Energy, 2006, 25(1): 39-43.

[11]李彪, 劉新正, 李黎川. 具有低通濾波的改進電壓模型磁鏈觀測器 [J]. 西安交通大學學報, 2009, 43(12): 91-95. LI Biao, LIU Xinzheng, LI Lichuan. Modified algorithm for voltage module flux estimation with low pass filter [J]. Journal of Xi’an Jiaotong University, 2009, 43(12): 91-95.

[12]孫大南, 林文立, 刁利軍, 等. 改進型感應(yīng)電機電壓模型磁鏈觀測器設(shè)計 [J]. 北京交通大學學報, 2011, 35(2): 94-98. SUN Danan, LIN Wenli, DIAO Lijun, et al. Improved voltage model flux observer design of induction machine [J]. Journal of Beijing Jiaotong University, 2011, 35(2): 94-98.

[13]史黎明, 王珂, 李耀華. 基于改進磁鏈觀測器的直線異步電動機直接牽引力控制 [J]. 電工技術(shù)學報, 2008, 23(9): 45-50. SHI Liming, WANG Ke, LI Yaohua. Direct thrust control of linear induction motor based on improved flux observer [J]. Transactions of China Electrotechnical Society, 2008, 23(9): 45-50.

[14]李紅, 羅裕, 韓邦成, 等. 帶通濾波器法電壓積分型定子磁鏈觀測器 [J]. 電機與控制學報, 2013, 17(9): 8-16. LI Hong, LUO Yu, HAN Bangcheng, et al. Voltage integral model for stator flux estimator based on band-pass filter [J]. Electric Machines and Control, 2013, 17(9): 8-16.

[15]WANG Yu, DENG Zhiquan. An integration algorithm for stator flux estimation of a direct-torque-controlled electrical excitation flux-switching generator [J]. IEEE Transactions on Energy Conversion, 2012, 27(2): 411-420

[16]文曉燕, 鄭瓊林, 韋克康, 等. 帶零漂補償和定子電阻自校正的磁鏈觀測器 [J]. 中國電機工程學報, 2011, 31(12): 102-107. WEN Xiaoyan, ZHENG Qionglin, WEI Kekang, et al. Flux observer with offset compensation and stator resistance self-correction [J]. Proceedings of the CSEE, 2011, 31(12): 102-107.

[17]韋立祥, 劉叢偉, 孫旭東, 等. 一種消除電壓型磁鏈觀測器中直流偏置誤差的新方法 [J]. 清華大學學報: 自然科學版, 2001, 41(9): 51-54. WEI Lixiang, LIU Congwei, SUN Xudong, et al. New integral error correction method for rotor flux identification of AC drives [J]. Journal of Tsinghua University: Sci & Tech, 2001, 41(9): 51-54.

[18]賈洪平, 賀益康. 一種適合DTC應(yīng)用的非線性正交反饋補償磁鏈觀測器 [J]. 中國電機工程學報, 2006, 26(1): 101-105. JIA Hongping, HE Yikang. A new nonlinear perpendicular flux observer with compensation feedback suit-

able for DTC application [J]. Proceedings of the CSEE, 2006, 26(1): 101-105.

[19]王子輝, 葉云岳. 反電勢算法的永磁同步電機無位置傳感器自啟動過程 [J]. 電機與控制學報, 2011, 15(10): 36-42. WANG Zihui, YE Yunyue. Research on self-startup states process of back-EMF based sensorless vector control of PMSM [J]. Electric Machines and Control, 2011, 15(10): 36-42.

(編輯 葛趙青)

New Flux Estimation Algorithms for Position Sensorless Control of Permanent Magnet Synchronous Motors

LI Biao,LI Lichuan

(School of Electrical Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Aiming at the problem that traditional flux estimation algorithms based on the voltage model would introduce magnitude and phase errors in steady state in the elliptical rotating magnetic field commonly existing in motors, two novel flux estimation algorithms were proposed based on the basic relationship between the back electromotive force (EMF) and the flux in steady state in time domain. They are simple in structure and easy to implement in industrial applications. The new algorithms have the same frequency characteristics as that of pure integrator at synchronous frequency, and there is no coupling inαandβphases. The new algorithms can estimate flux exactly either in circular rotating magnetic field or in elliptical rotating magnetic field, since neither the symmetry of theαandβphases nor the orthogonality of the flux vector and the back EMF vector is needed. Simulation results show that the new algorithms could effectively eliminate the integration drift, and realize errorless flux estimation in steady state. The new algorithms were used for the rotor position estimation in the position sensorless vector control of a surface-mounted permanent magnet synchronous motor (SPMSM). Experiment was performed using a digital signal processor TMS320F2812DSP. Experimental results show that the new algorithms have fine speed and position tracking effect when operating at a speed 10% above the rated value, but in the low-speed region, there will be unstable estimation results. The speed control system has good steady-state performance since the new algorithms can exactly estimate the magnitude and phase of flux. The speed control system also has good dynamic characteristics due to the high flux estimation accuracy of the new algorithms when the motor speed has an abrupt change.

flux estimation; elliptical rotating magnetic field; permanent magnet synchronous motor; position sensorless vector control

2015-02-04。

李彪(1983—),男,博士生;李黎川(通信作者),男,教授,博士生導(dǎo)師。

時間:2015-08-26

10.7652/xjtuxb201511017

TM301.2

A

0253-987X(2015)11-0102-08

網(wǎng)絡(luò)出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20150826.1117.002.html