精密軌道定位方法的改進

任 鍇，唐穎哲，馮來平，歐陽明達

精密軌道定位方法的改進

任 鍇1，2，唐穎哲3，馮來平3，歐陽明達1，2

( 1．信息工程大學地理空間信息學院，河南鄭州450052; 2．西安測繪信息技術總站，陜西西安710054; 3．西安測繪研究所，陜西西安710054)

一、引言

文獻［1］在GPS動態定位應用中，推導了一種利用多參考站和高精度軌道，采用非差觀測值，同步計算測站位置和衛星鐘差的定位方法，且將此方法命名為精密軌道定位( precise orbits positioning，POP)方法。對距基站數百千米至上千千米長度的流動站，比較了該方法與PPP( precise point positioning)方法的計算結果，結果表明在收斂速度、測站精度方面，該方法都有一定優勢。

本文對該方法進行了分析，在兩個方面進行了擴展:一是通過對靜態測站數據處理，將對高精度軌道的要求進行了擴展，計算表明，完全可以采用廣播星歷;二是對包括基站同步處理的非差觀測數據進行整周模糊度約束，將結果由模糊度實數解擴展到固定解。采用IGS網站數據進行了計算，結果表明，本文在這兩方面的擴展是合理的，方法具有一定參考價值。

二、POP原理

PPP解算需要高精度的衛星軌道和鐘差產品［2］，在實時應用中，高精度的軌道可以通過預報得到。如IGS的超快速軌道產品，它就是通過24 h的實測數據定軌并外推24 h，提供48 h軌道產品，每6 h更新一次，超快速軌道產品預報軌道的精度可以達到5 cm［3］。而預報衛星高精度鐘差產品是比較困難的，原因是衛星鐘噪聲影響難以建模，因此，在沒有高精度衛星鐘差的情況下，無法進行基于非差方法的PPP解算。

文獻［1］利用多個位置已知的基站，采用高精度軌道產品，仍采用非差觀測數據，同步估計衛星鐘差和流動站位置，以達到流動站高精度定位的目的。由于所有衛星鐘差和接收機鐘差設為未知參數時，將使法方程病態，因此只能計算相對鐘差。即將其中的一個基站接收機鐘差固定，該站稱為主站，因此在該方法中，數據處理包括主站、基站和待定站。

觀測值采用無電離層影響的偽距和載波相位組合，主站0觀測衛星j的觀測方程為

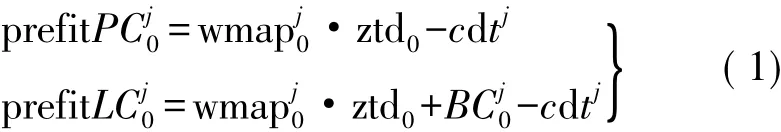
式中，左側分別為偽距和相位的觀測值減計算值，計算值的各項改正處理除衛星鐘差外與PPP方法相同; ztd0為對流層天頂延遲參數; wmapj0為濕延遲映射函數值; dtj為衛星鐘差; c為真空中光速; BCj0為初始模糊度參數。

基站i觀測衛星j的觀測方程為

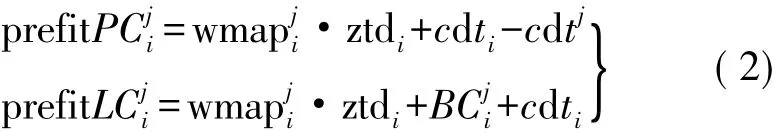
式中，dti為接收機鐘差;其余量含義同主站，只是對應于基站i。

待定站r觀測衛星j的觀測方程為

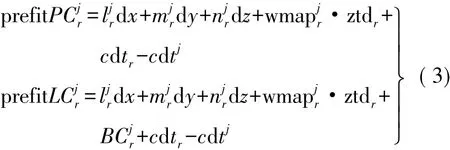
式中，( dx，dy，dz)為測站位置參數(相對于初始值的改正值) ; ( l，m，n)為測站到衛星的方向余弦;其余量定義同前，對應為測站r。

對上述3組方程分析可見，雖采用的是非差觀測值，但通過衛星鐘差這個參數，將3組方程聯系到一起。文獻［1］認為可相似于組差。

既然可相似于組差，那么組差主要在高精度相對定位中應用，在相對定位中，尤其是中短距離的基線解中，軌道精度影響有限，廣播星歷計算的軌道即可滿足高精度的基線解算。因此，可以將POP方法擴展到利用廣播星歷進行處理，本文算例支持了這種擴展。

由于有同步處理的主站和基站觀測值，因此，在事后處理中，在得到高精度的非差模糊度實數解之后，可以進一步利用多站同步觀測值，構建雙差觀測值，利用雙差模糊度的整數特性，構建對原始非差模糊度的約束值，從而利用這種約束值得到非差模糊度固定解。這是本文對POP方法的第二處擴展。

三、非差模糊度固定原理

對主站、基站、待定站組成的測站網，本文采用的非差模糊度固定解算法，有的文獻稱為MW方法［4］。在實數解之后，主要的數據處理過程包括:非差到雙差的映射關系確定，獨立雙差模糊度集的確定，雙差寬巷、窄巷模糊度整數值的確定，雙差無電離層相位模糊度約束值的確定，加入這些約束值后的平差計算。要詳細進行闡釋則需較長篇幅，本文對處理過程中用到的有關關系式進行簡述，對于細節讀者可參考有關文獻［5-6］。

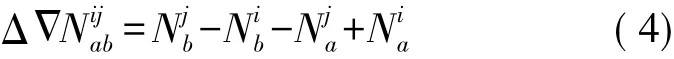
式中，下標a、b代表測站;上標i、j代表衛星;ΔΔ表示雙差算子;式中右側為有關站星非差模糊度，左側為組合的雙差模糊度，一個雙差由4個非差構成。式( 4)為非差到雙差的映射關系，通過該映射，可以將寬巷、窄巷、無電離層組合非差模糊度映射到相應的寬巷、窄巷、無電離層組合雙差模糊度。對于一個雙差，可形成一個映射向量，對于全部雙差可得到一個映射矩陣。

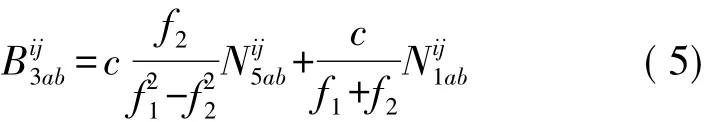
式中，f1、f2代表GPS的兩個載波頻率值; Ni5jab為寬巷雙差模糊度; N1ijab為窄巷雙差模糊度; B3ijab為無電離層組合雙差模糊度。式( 5)即反映了寬巷、窄巷、無電離層組合雙差模糊度關系，在數據處理過程中，先通過原始觀測值的MW組合計算非差寬巷模糊度，再利用映射關系得到寬巷雙差模糊度值。初始無電離層組合雙差模糊度由平差解算后的非差實數解映射得到，通過該關系式計算得到窄巷雙差模糊度。

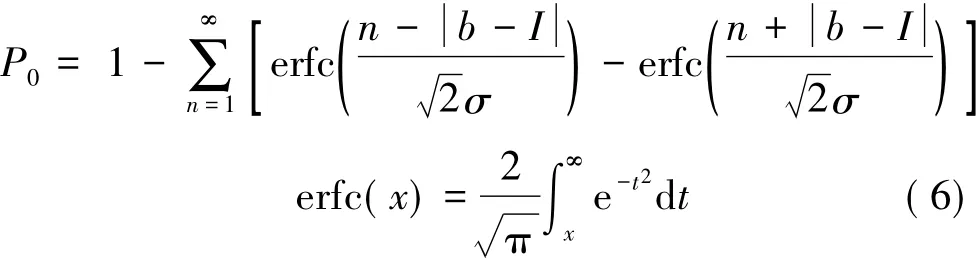
式中，b、σ為雙差模糊度實數值及其方差; I為取整后的雙差模糊度整數值; P0為概率值; n的上限實用上取一個小值［7］。式( 6)即為寬巷、窄巷模糊度實數值能否取為整數值的判定函數。由于計算精度有保證，因此可直接采用取整法來確定模糊度整數值，但需對取整是否合理進行判定。在一定置信水平α下，滿足P0＞1－α關系的認為是合理的，否則，雙差模糊度仍按實數處理。在取得雙差寬巷、窄巷整數模糊度值后，利用式( 5)，計算無電離層組合雙差模糊度新值，可得

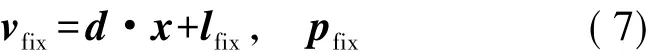
式中，d為式( 4)形成的非差到雙差的映射向量; x為待定非差模糊度參數; lfix為初始無電離層組合雙差模糊度與無電離層組合雙差模糊度新值之差; pfix為權; vfix為驗后殘差。式( 7)構成對非差模糊度參數的約束關系。與相對定位不同，無電離層組合雙差模糊度新值不能直接固定后重解其他參數，而只能是通過式( 4)的映射關系，對相應非差模糊度參數進行約束，采用附有約束條件的平差方法處理，解算全體參數。

四、計算與比較

1．數據情況

本文算例采用IGS網站提供的4個測站2013 年40天GPS觀測數據，采樣間隔為30 s，測站分布如圖1所示。將BLYT設為待定站，其余為基站，待定站與最近的基站BILL距離為218．3 km，與最遠的基站AZUl距離為299．8 km，設AZUl為主站。所有測站坐標通過IGS事后產品采用PPP計算，并作為已知值。廣播星歷和IGS快速星歷由IGS網站下載，并將快速星歷進行拼接，得到40天僅含快速預報軌道的精密星歷文件。

2．計算方法

首先進行靜態處理。對全天數據進行處理，分別采用1 h、2 h、3 h時段長度，每1 h滑動一個計算窗口，分別得到23、22、21個時段的計算結果，統計計算值與已知值差的RMS(均方差)。計算時分別采用IGS事后星歷、快速星歷和廣播星歷，并進行實數解和模糊度固定解計算。

之后進行動態解算。將BLYT設為動態站，利用快速星歷和廣播星歷進行了0～3 h的動態定位，統計模糊度實數解結果。

3．計算結果

( 1)靜態定位結果

BLYT測站靜態定位結果與已知值差E、N、U分量RMS統計情況見表1。

圖1 測站分布

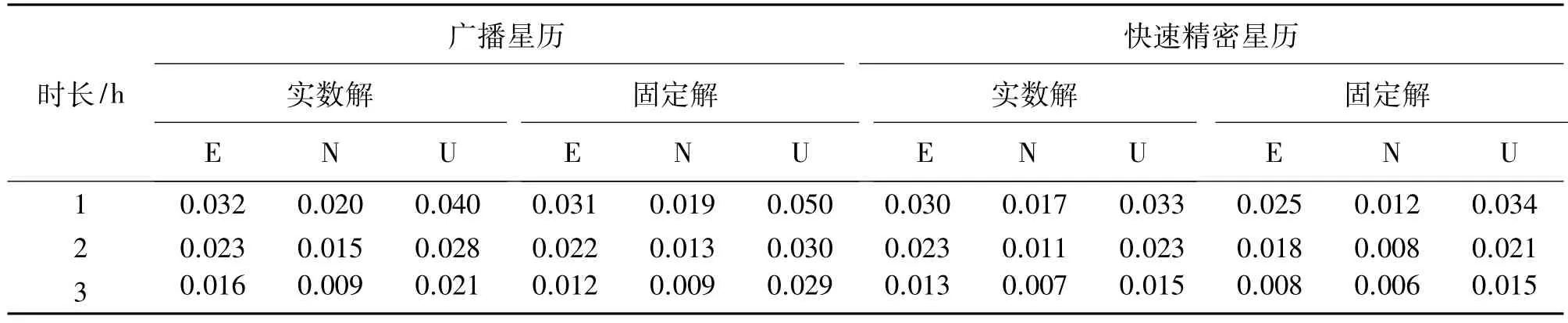
表1 靜態定位結果RMS值統計m

由計算結果可以看出，增加觀測時長對提高定位精度有幫助;軌道精度對提高點位精度有明顯影響;模糊度固定解在E分量相對實數解精度提高明顯，N分量精度略有提高，U分量有的時段精度有下降情況; 3 h時段快速精密星歷模糊度固定解，水平分量RMS達到毫米級精度，U分量精度達到1．5 cm; 3 h時段廣播星歷模糊度固定解，水平分量RMS達到1．2 cm，U分量精度達到2．9 cm。

采用事后精密星歷結果與快速精密星歷結果完全相同，說明快速預報的軌道精度已較高，與事后軌道計算結果一致。

( 2)動態定位結果

統計BLYT站分別利用廣播星歷和快速精密星歷的動態定位結果，統計時均去除了前30 min數據，對余下的300個歷元計算結果與已知值差E、N、U分量RMS、最大值、最小值進行統計，結果見表2。

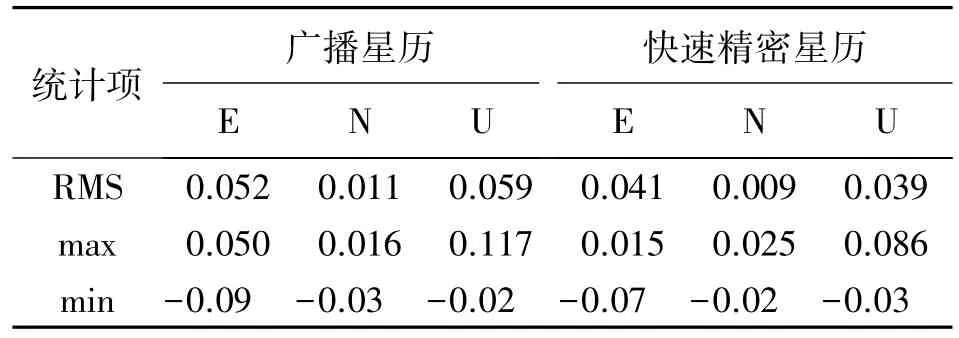
表2 動態定位結果統計 m

由計算結果可知，軌道精度對定位結果有明顯影響;廣播星歷動態定位結果E分量RMS達到5．2 cm，N分量RMS達到1．1 cm，U分量RMS達到5．9 cm，均在厘米級。

五、結束語

本文對POP方法進行了擴展，在距基站中短距離的待定站靜態、動態數據處理中，通過廣播星歷的應用，避免了對高精度軌道的依賴;在靜態數據處理中，利用模糊度固定解，可以在水平分量精度上比模糊度實數解有所提高。實例表明了本文方法的可行性，具有一定的應用價值。

［1］ SALAZAR D．Precise GPS-based Position，Velocity and Acceleration Determination: Algorithms and Tools［D］．Spain: Technical University of Catalonia，2010．

［2］ KOUBA J．A Guide to Using International GNSS Service ( IGS) Products［R］．［S．l．］: NASA，2009．

［3］ IGS．IGS_strategic_plan_2013_Final［EB/OL］．［2014-07-20］．http:∥www．igs．org/publications/IGS_ Strategic _Plan_2013_Final．pdf．

［4］ 周巍，馮來平，王永收，等．QIF和MW模糊度分解方法的比較［J］．大地測量與地球動力學，2013，33 ( 5) : 86-90．

［5］ GE M，GENDT G，DICK G，et al．A New Data Processing Strategy for Huge GNSS Global Networks［J］．Journal of Geodesy，2006，80( 4) : 199-203．

［6］ GE M，GENDT G，DICK G，et al．Improving Carrierphase Ambiguity Resolution in Global GPS Network Solutions［J］．Journal of Geodesy，2005，79( 1-3) : 103-110．

［7］ ESOC．NAPEOS Mathematical Models and Algorithms ［M］．European Space Agency:［s．n．］，2009．

The Improvement of Precise Orbit Positioning Method

REN Kai，TANG Yingzhe，FENG Laiping，OUYANG Mingda

通過對精密軌道定位( POP)方法的深入分析，從兩個方面對其進行了擴展:一是利用廣播星歷進行數據解算，使得在距基站中短距離的待定站高精度定位時，避免了對高精度軌道的依賴;二是利用模糊度固定方法，將模糊度實數解擴展到模糊度固定解，解算精度得到了進一步提高。通過一組實際觀測數據的處理，驗證了本文方法的可行性，具有一定的實用價值。

GPS;精密軌道定位; PPP;模糊度固定

任 鍇( 1973—)，男，博士生，工程師，主要從事GNSS理論研究和數據處理。E-mail: Rpvt1204@ 163．com

P228．4

B

0494-0911( 2015) 11-0008-03

任鍇，唐穎哲，馮來平，等．精密軌道定位方法的改進［J］．測繪通報，2015( 11) : 8-10．

10．13474/j．cnki．11-2246．2015．0334

2014-11-16

國家自然科學基金( 41474015)