線陣CCD傾斜布置敏捷衛星輻射定標的姿態計算方法

李海超 滿益云

（錢學森空間技術實驗室，北京 100094）

線陣CCD傾斜布置敏捷衛星輻射定標的姿態計算方法

李海超 滿益云

（錢學森空間技術實驗室，北京 100094）

針對搭載傾斜布置的多片線陣CCD相機的敏捷衛星上所有探測器對同一區域成像的相對輻射定標，提出了基于地面成像軌跡重合的偏航角速度計算模型與方法，充分利用敏捷衛星對偏航角速度的控制潛力。建立了地面物點到相機焦平面的空間坐標變換關系；推導了斜視成像時地心角的計算公式；給出了對同一區域成像的敏捷衛星偏航角速度計算方法。以5片線陣CCD共30 000個探測器、相鄰兩片傾斜0.3°的敏捷衛星作為仿真對象，給出了所有探測器在約30 s的定標成像過程中的地面軌跡間隔寬度，結果表明：為了實現所有探測器對同一區域成像，需要間隔一定周期調整偏航角速度，當調整周期為0.36 s時，對應的地面軌跡寬度在赤道附近優于1個像元、在緯度50°附近優于6個像元。文章對敏捷衛星基于同一區域成像的相對輻射定標可提供一定的參考價值。

敏捷衛星；線陣CCD相機；相對輻射定標；地面軌跡；偏航角速度

1 引言

遙感圖像的質量由獲取的圖像數據質量與圖像處理的質量兩方面決定，而圖像數據的獲取質量由遙感器的綜合性能決定。由于光學遙感器中各探測器之間的響應特性不一致，對于同樣輸入的輻射能量其輸出響應存在一定差異，在獲取的圖像中表現為條帶現象［1］。因此，為獲取高質量的遙感圖像，遙感器有必要進行相對輻射定標，給出每個探測器的相對輻射定標系數，以消除或降低各個探測器之間的響應不一致性帶來的影響。目前，在軌衛星的相對輻射定標主要通過地面均勻場地、在軌遙感圖像統計等手段實現。然而，地面均勻場地法需要尋找或鋪設足夠大的均勻場地，如自然湖泊、草原、冰川、人工定標場等，其特點是尋找難度大、建設成本高；目前應用較廣的在軌遙感圖像統計方法［2-3］，需要多軌圖像數據，因此，該類方法的前提是確保各軌圖像數據的穩定性。

隨著遙感衛星技術的發展，具備敏捷機動能力的衛星已經成為遙感衛星的一個重要發展方向［4］。國外近幾年廣泛應用的Side-Slither定標方法［5］，正是利用了衛星敏捷的姿態控制將衛星偏航角旋轉90°，使得多片線陣CCD對同一區域成像成為可能，實現了所有的探測器對同一區域成像的相對輻射定標。近年來，以法國昴宿星（Pleiades）為代表的敏捷衛星，為減小光學畸變的影響，該衛星的全色譜段探測器采取將5片線陣CCD陣列傾斜布置在焦平面上，用“弧線”形狀代替常用的“直線”形狀布置方式［6］。因此，對于這類傾斜布置的線陣CCD實現Side-Slither定標，需要借助衛星較強的敏捷能力。

本文為實現對同一區域成像的相對輻射定標，提供一種多片傾斜布置的敏捷衛星偏航角速度計算方法：建立了衛星斜視成像的空間坐標變換關系；在此基礎上，給出了基于空間坐標變換關系的對同一區域成像的衛星偏航角速度計算方法；定標成像過程中根據敏捷衛星姿態控制能力不斷調整衛星偏航角速度。

2 衛星斜視成像坐標系轉換

2.1 坐標系定義

從地面景物到光學遙感器的坐標變化過程中，需要定義如下7個坐標系［7］，本文中坐標系一律采用右手坐標系：

（1）衛星軌道坐標系B（B0-B1B2B3）：原點B0在軌道上，B1軸在軌道面上指向衛星飛行方向，B3軸過地心并指向天頂，B2軸與軌道面垂直，衛星以角速度Ω在軌道上運動。

（2）衛星本體坐標系S（S0-S1S2S3）：原點S0與B0重合，衛星無姿態運動時S與B系重合，滾動角φ、俯仰角θ、偏航角ψ即指S系在B系內的三軸姿態（順序φ→θ→ψ）。

（3）相機坐標系C（C0-C1C2C3）：無安裝誤差時相機坐標系與本體坐標系重合。

（4）焦平面坐標系P（P0-P1P2P3）：多片線陣CCD的中點P0為焦平面坐標系的原點；P1，P2，P3三個坐標軸過P0點，且分別平行于本體坐標系的滾動軸、俯仰軸和偏航軸。

（5）地面坐標系G（G0-G1G2G3）：原點G0為P0在地面的成像點，G1軸平行于衛星飛行方向，G3軸過地心指向天頂，G2軸垂直于G1G3構成的平面。

（6）參考坐標系I（O-I1I2I3）：原點O在地心，I2軸指向北極，I3軸指向衛星軌道升交點，I1軸垂直I2和I3構成的平面。

（7）固定坐標系E（O-E1E2E3）：該坐標系固聯于地球，原點O與I系原點重合（在地心），E2軸指向北極，與I2軸重合，該坐標系在I坐標系內繞E2（即I2）、逆時針方向以地球角速度ω自轉，該坐標系在起始時刻與I系重合。

2.2 衛星斜視成像的坐標變換

為適應衛星斜視成像的需求，本文給出了非星下點斜視成像的坐標變換模型。圖1為斜視成像示意圖，其對應的從地面坐標系G到焦平面坐標系P的坐標轉換順序見表1。

根據表1和圖1，可得到地面坐標系G中的點（G1，G2，G3）到焦平面坐標系P中的點（P1，P2，P3）的變換關系，為表示兩個坐標系間的平移、旋轉和縮放，采用齊次坐標變換矩陣表示見式（1）。

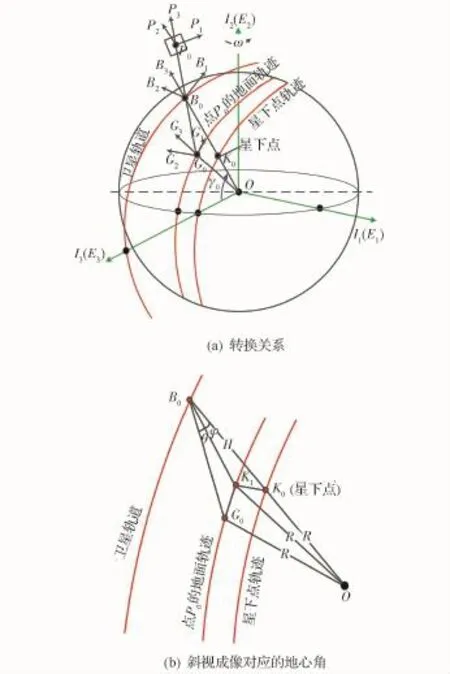
圖1 從地面坐標系G到焦平面坐標系PFig.1 Transformation from ground coordinate G to focal plane coordinate P

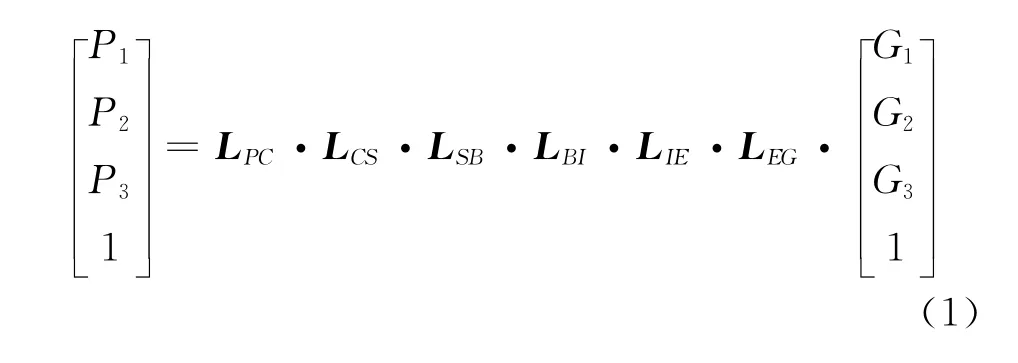
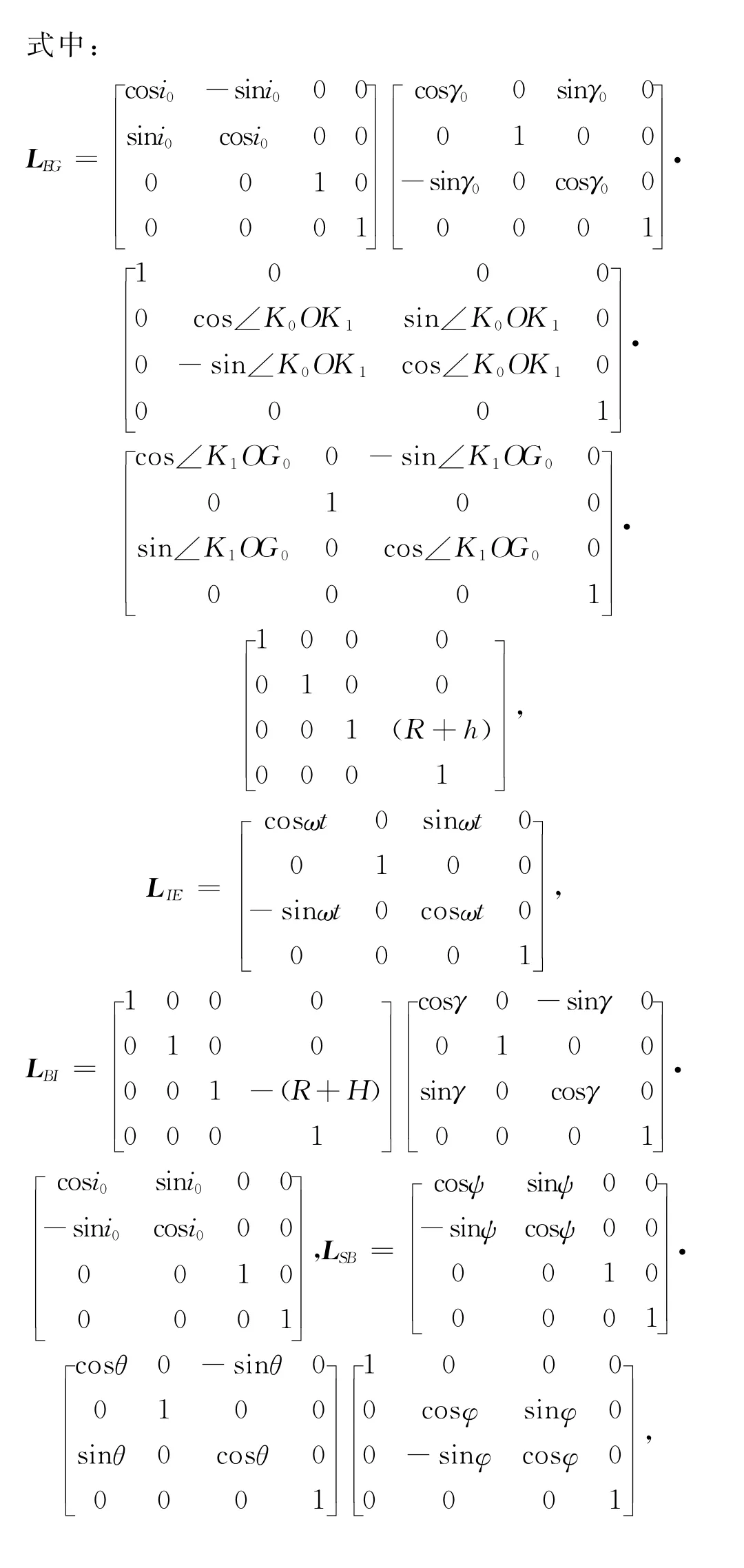
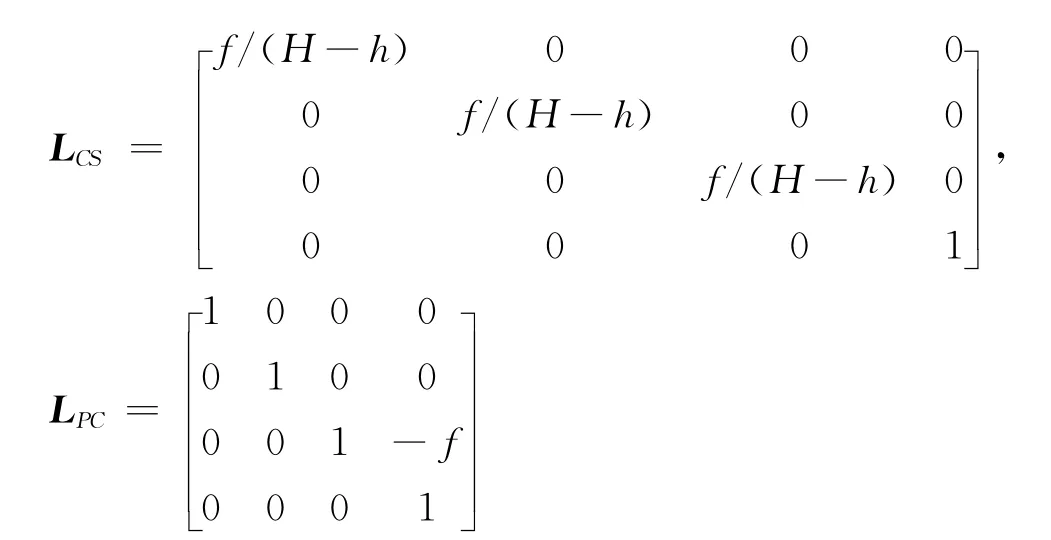
其中，R為地球半徑；h為地面點G0的地形高度；H為航天器的軌道高度；f為相機焦距；γ＝γ0＋Ωt，γ0為攝影時刻升交點與衛星之間所對應的地心角，Ω為衛星軌道運行相對地心的角速度；i0為衛星軌道傾角；ω為地球自轉角速度；ψ＝ψ0＋dψt，θ＝θ0＋dθt，φ＝φ0＋dφt；ψ0、θ0、φ0分別表示衛星的初始偏航角、俯仰角、滾動角，dψ，dθ，dφ分別表示衛星的偏航、俯仰和滾動角速度。

圖1（b）所示，∠K0OK1和∠K1OG0是衛星斜視成像對應的地心角，計算方法如下。

在ΔB0OK1中：

3 衛星偏航角速度計算方法

圖2是衛星從常規成像模式進入在軌定標成像模式的示意圖，其中，軌道S位置為常規成像模式，此時首先計算衛星對應的初始偏流角：

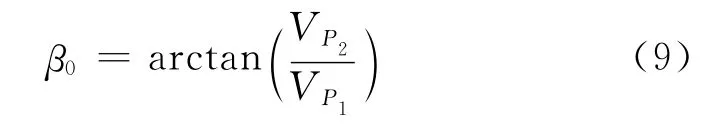
其中，VP1和VP2分別為相機像面的前向像移速度和橫向像移速度。設定某一時刻地面上一物點經過相機成像，對應的像點的坐標為（P11，P21），經過足夠短的時間Δt之后，該地面上的物點在像平面上的像點運動到（P12，P22）位置處，利用差分法計算像移速度［8］：

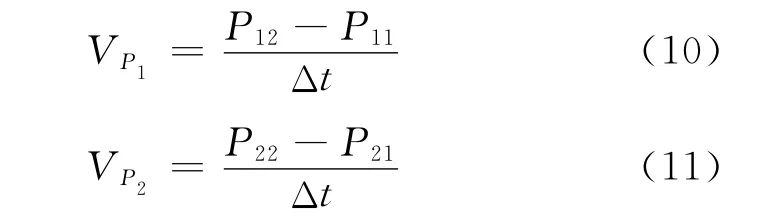
然后，經過衛星偏航角旋轉90°―β0的姿態調整，在S0位置衛星進入相對輻射定標成像模式。考慮偏流角β0的主要目的是消除地球自轉對成像的影響［9-10］。

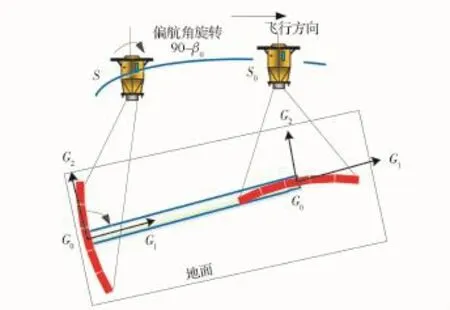
圖2 從常規成像模式進入在軌定標成像模式Fig.2 From conventional imaging to on-orbit calibration imaging

3.1 傾斜布置的線陣CCD相對輻射定標原理

根據Side-Slither相對輻射定標原理［5］，線陣CCD的所有探測器應該依次對地面同一區域成像（即要求所有探測器的地面成像軌跡理論上應該重合），獲取同一區域的成像數據。對于傾斜布置的多片線陣CCD的相對輻射定標原理描述如下：

如圖3（a）所示，設定位置S0為衛星進行相對輻射定標成像的起始位置（對于時刻t0＝0）；如圖3（b）所示，該位置所對應的焦平面坐標系作為原焦平面坐標系P0-P1P2P3，對應的地面坐標系作為原地面坐標系G0-G1G2G3。則此時線陣CCD對應的地面軌跡稱為初始地面軌跡。

隨著衛星在軌道的運動，原焦平面坐標系以線陣CCD的像元尺寸de作為步長沿著衛星飛行方向進行平移，同時原焦平面坐標系繞著坐標原點P0以偏航角速度進行旋轉。經過時間t1＝n1×te后，原焦平面坐標系的原點P0運動到新焦平面坐標系P0＇-P1＇P2＇P3＇的原點P0＇，衛星到達位置S1，如圖3（c）所示，其中te為曝光時間，n1為原焦平面坐標系移動的像元個數。此時刻線陣CCD對應的地面軌跡理論上應該要求與初始地面軌跡重合。

由于本文中多片線陣CCD的傾斜布置，為確保所有探測器先后依次對地面同一區域成像，因此，成像過程中必須對衛星偏航角速度進行不斷調整。

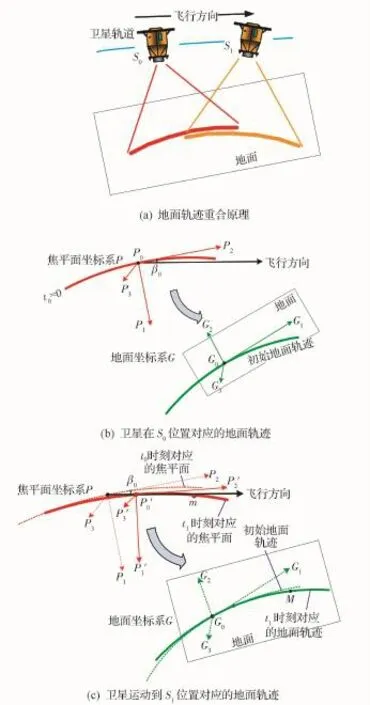
圖3 其地面軌跡作為條件計算偏航角速度的示意圖Fig.3 Diagram of satellite YAV computation for all CCD detectors passed through the same trajectories

3.2 偏航角速度計算步驟

為實現對同一區域成像的偏航角速度計算方法分為以下6個步驟：

（1）在t0時刻根據式（1）計算傾斜布置的線陣CCD對應的初始地面軌跡，如圖3（b）所示。

（2）經過時間t1到達位置S1之后，如圖3（c）所示，P0＇在原焦平面坐標系中的坐標P0＇_old（p10＇_old，p20＇_old，0）計算為：

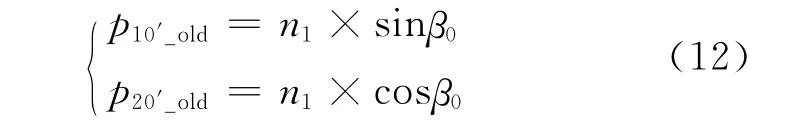
（3）設定從t0時刻（位置S0）開始，衛星以偏航角速度運動，則從t0到t1時間段內，衛星偏航角旋轉的大小為Δβ＝t1×，即P0＇-P1＇P2＇P3＇坐標系相對P0-P1P2P3坐標系旋轉的角度。

（4）計算t1時刻傾斜布置的線陣CCD對應的地面軌跡：①設線陣CCD的任意點m在新焦平面坐標系中的坐標表示為（p1m_new，p2m_new，0），該坐標由線陣CCD在焦平面上的數學模型計算得到；②根據P0-P1P2P3和P0＇-P1＇P2＇P3＇之間的旋轉與平移關系，點m在原焦平面坐標系中的坐標（p1m_old，p2m_old，0）計算公式見式（13）；③根據式（1）計算（p1m_old，p2m_old，0）在原地面坐標系G0-G1G2G3中對應的坐標（g1M，g2M，0）；④重復步驟①～③計算其它點的坐標，得到線陣CCD對應的地面軌跡。

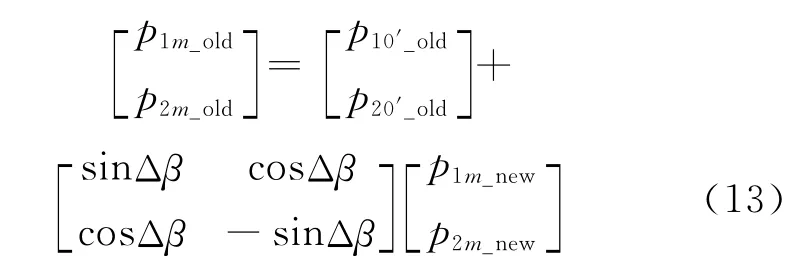
（6）計算（5）中與初始地面軌跡距離最近的地面軌跡，其所對應的角速度即所求的偏航角速度。

4 仿真實驗與分析

本文仿真數據：5片線陣CCD傾斜布置，相鄰兩片夾角0.3°，每片CCD有L＝6000個探測器，一共30 000個探測器，焦距2.6 m，積分時間362.59μs；衛星軌道高度H＝645.338 km，地球半徑R＝6 378.137 km，衛星軌道周期98min，軌道傾角98°。

焦平面坐標系如圖4所示，其中實際在軌運行時，5片傾斜布置的線陣CCD的數學模型可以通過在軌定標得到，本仿真實驗中用圓擬合來建立線陣CCD的數學模型，將5片CCD的首末端點和中點共11個探測器，即圖中的點A～J，作為分析對象，根據它們的地面軌跡來計算偏航角速度。

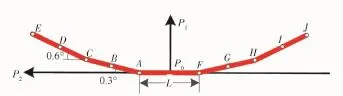
圖4 焦平面坐標系Fig.4 Focal plane coordinate

4.1 赤道附近、偏航角速度調整周期

在t0＝0時刻成像對應的緯度是0°、滾動角0°、控制偏航角速度的調整周期為0.36 s條件下，得到在大約32 s時間內成像的地面軌跡如圖5所示，5片CCD中11個探測器的地面軌跡用不同的曲線表示。其中，圖5（a）為大約32 s時間內的整個軌跡，圖中紅色虛線框區域是11個探測器都經過的區域，統計得到整個紅色虛線框區域內的地面軌跡間距均值為2.157 m（其中，地面軌跡間距定義為11個探測器地面軌跡的最大距離，如圖5（b）所示）；為了清楚表示多個探測器之間的地面軌跡情況，如圖5（b）給出了圖5（a）中的區域1的放大圖；圖5（c）是調整周期0.36 s下的衛星偏航角速度變化曲線，可以看出，為獲得圖5（a）的地面軌跡，偏航角速度變化趨勢先增大后減小，從―0.067 61（°）/s增大到―0.066 17（°）/s，再降低到―0.067 47（°）/s。

4.2 緯度40°附近、偏航角速度調整周期

在t0＝0時刻成像對應的緯度是北緯40°、滾動角0°、控制偏航角速度的調整周期為3.6 s條件下，得到線陣CCD中的11個探測器對應的地面軌跡如圖6所示。其中，圖6（a）中的紅色虛線框區域是11個探測器都經過的區域，統計得到整個紅色虛線框區域內的軌跡距離平均值為31.05 m；圖6（b）給出了圖6（a）中區域2的放大圖，在該區域內探測器點E與點J對應的地面軌跡間距最大，約為21 m；圖6（c）是偏航角速度變化曲線。

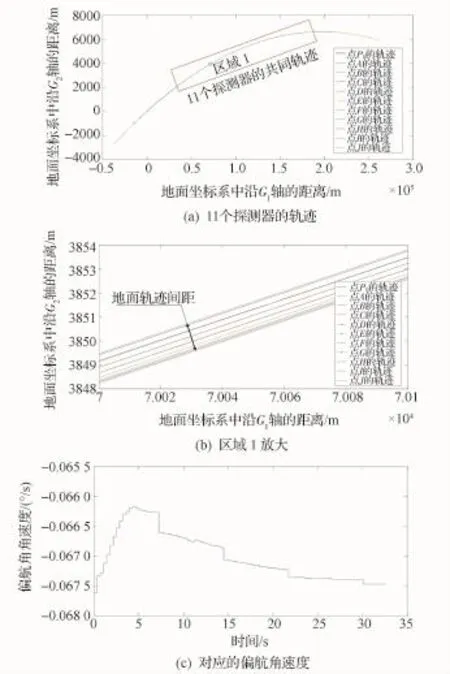
圖5 五片陣列中11個探測器的地面軌跡（赤道附近，偏航角速度調整周期為0.36 s）Fig.5 Trajectories of 11 detectors in 5 arrays（latitude 0°，YAV adjusting period is 0.36s）

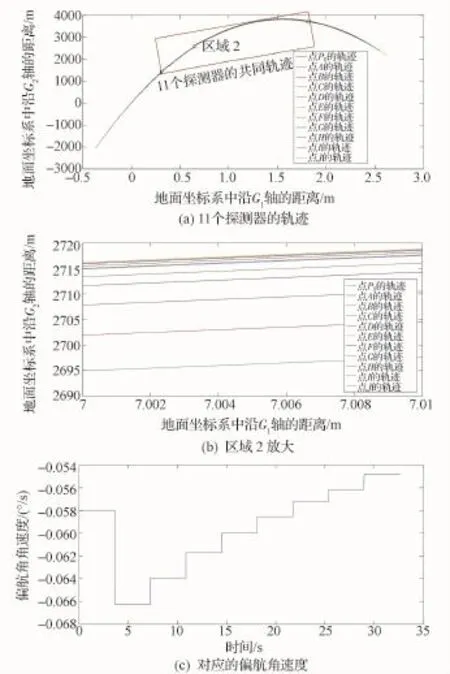
圖6 五片陣列中11個探測器的地面軌跡（北緯40°，偏航角速度調整周期為3.6 s）Fig.6 Trajectories of 11 detectors in 5 arrays（latitude 40°N，YAV adjusting period is 3.6s）

4.3 不同緯度不同滾動角下的地面軌跡間距分析

表2給出偏航角速度調整周期0.36 s條件下，給出了在不同緯度、不同滾動角成像時所對應的地面軌跡間距。可以看出，赤道附近對應的地面軌跡間距非常窄，例如緯度0°對應的地面軌跡間距2.157 m，5°對應的地面軌跡間距為1.378 m，因此低緯度區域的地面軌跡間距優于1個像元（對于2.5 m分辨率來說）。隨著緯度的增大，地面軌跡間距越來越寬，達到50°時，間距達到了15 m（對于2.5 m分辨率來說為6個像元）。低緯度赤道附近的軌跡間距隨著滾動角的增大變化明顯，例如，滾動角從0°到40°其對應的軌跡間距從2.157 m變化到22.287 m。

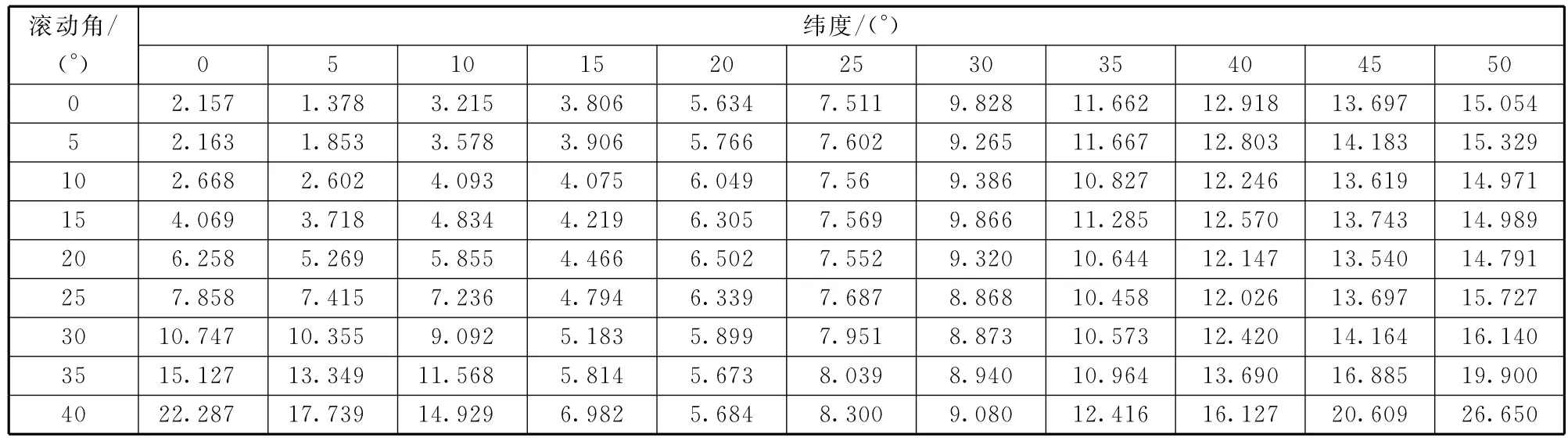
表2 不同緯度不同滾動角下的地面軌跡間距Table 2 Trajectory interval at different latitudes and roll angles m

4.4 地面軌跡間距誤差影響因素及不確定性分析

由于軌跡計算的不確定性，計算軌跡與實際軌跡引起了誤差，引起偏航角速度計算誤差的主要影響因素有姿態角（設定最大測量誤差0.01°）、姿態角速度（設定最大測量誤差0.001°）、軌道高度（設定最大測量誤差100 m）、地心角（設定最大測量誤差0.1°）等。

本部分對衛星在緯度0°、滾動角0°執行定標成像時，各個誤差因素引起的地面軌跡間距的不確定性進行定量分析。由于各個誤差因素的最大測量誤差不一致，為便于在圖中表示，用橫坐標表示最大誤差的倍數（0.1、0.2、……1.0），如圖7所示。

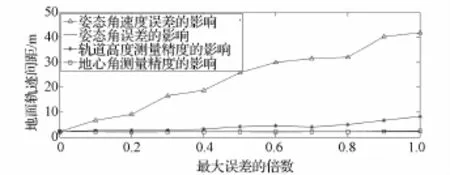
圖7 不同參數誤差帶來的地面軌跡間距的誤差Fig.7 Trajectory interval error caused by various error factors

從圖7中可以看出，姿態角速率測量誤差對地面軌跡間距的影響程度最大，隨著姿態角速率測量精度的下降，引起的地面軌跡間距急劇增大，軌跡間距從2.157 m（姿態角速率無誤差）下降到41.837 m（姿態角速率誤差0.001（°）/s），因此，為確保所有探測器對同一區域成像，姿態角速率測量精度應該嚴格要求；軌道高度測量精度對地面軌跡間距也有一定的影響，軌跡間距從2.157 m（軌道高度無測量誤差）下降到8.347 m（軌道高度誤差100 m）；姿態角和地心角測量精度對軌跡間距幾乎不產生影響。因此，為滿足相對輻射定標需求的同一區域成像這一條件，應該重點減小姿態角速率的測量誤差。

5 結束語

在定標成像模式下執行傾斜布置線陣CCD的Side-Slither相對輻射定標時，需要所有探測器對同一個區域進行成像，較目前傳統的相對輻射定標方法，建立了相同的輸入數據源。本文提出了基于嚴密數學模型的傾斜布置多片線陣CCD相機的相對輻射定標方法，建立了斜視成像條件下從地理坐標系到焦平面坐標系的轉換關系，據此計算衛星偏航角速度，適應于斜視成像的相對輻射定標。

從仿真實驗可以看出，理論上通過控制衛星姿態可以得到較小的地面軌跡間距，使得所有探測器近似地依次對地面同一區域成像，但是，對衛星姿態控制要求較高，這對于在軌衛星實現難度大。因此，在軌進行Side-Slither相對輻射定標時，為降低對衛星姿態控制的要求，可以選擇具有一定寬度的均勻地面場景，從而可以適當放寬對地面軌跡間距的限制約束，根本上降低對衛星姿態控制的要求。

（References）

［1］Corsini G，Diani M，Walzel T.Striping removal in MOS-B data［J］.IEEE Transactions on Geoscience and Remote Sensing，2000，38（3）：1439-1446

［2］Horn B K P，Woodham R J.Destriping Landsat MSS images by histogram modification［J］.Computer Graphics and Image Processing，1979，10：69-83

［3］Gadallah F L，Csillag F，Smith E J M.Destriping multi sensor imagery with moment matching［J］.International Journal of Remote Sensing，2000，21：2505-2511

［4］張新偉，戴君，劉付強.敏捷遙感衛星工作模式研究［J］.航天器工程，2011，20（4）：32-38 Zhang Xinwei，Dai Jun，Liu Fuqiang.Satellite with agile attitude control［J］.Spacecraft Engineering，2011，20（4）：32-38（in Chinese）

［5］Cody A，Denis N，Andreas B，et al.Radiometric correction of Rapid Eye Imagery using the on-orbit sideslither method［C］//SPIE 8180，Image and Signal Processing for Remote Sensing XVII.Bellingham：SPIE，2011

［6］Baillarin S，Lebegue L，Kubik P.PLEIADES-HR system qualification：a focus on ground processing and image products performances，a few months before launch［C］.Proceedings IGARSS.New York：IEEE，2009

［7］王家騏，于平，顏昌翔，等.航天光學遙感器像移速度矢計算數學模型［J］.光學學報，2004，24（12）：1585-1588 Wang Jiaqi，Yu Ping，Yan Changxiang，et al.Space optical remote sensor image motion velocity vector computational modeling［J］.Acta Optica Sinica，2004，24（12）：1585-1588（in Chinese）

［8］王運，顏昌翔.基于差分法的空間相機像移速度矢量計算［J］.光學精密工程，2011，19（5）：1054-1060 Wang Yun，Yan Changxiang.Computation of image motion velocity vector for space camera based on difference method［J］.Optics and Precision Engineering，2011，19（5）：1054-1060（in Chinese）

［9］景泉.敏捷衛星偏流角計算模型研究［J］.航天器工程，2012，21（4）：16-20 Jing Quan.Research on computation model of bias angle for agile satellite［J］.Spacecraft Engineering，2012，21（4）：16-20（in Chinese）

［10］朱興鴻，邸國棟，陸春玲.一種遙感衛星偏流角修正的仿真分析方法［J］.航天器工程，2013，22（1）：39-43 Zhu Xinghong，Di Guodong，Lu Chunling.Simulation analysis on drift angle adjustment for remote sensing satellite［J］.Spacecraft Engineering，2013，22（1）：39-43（in Chinese）

（編輯：李多）

Attitude Computation of Radiometric Calibration for Agile Satellite with Tilted Linear CCD

LI Haichao MAN Yiyun
（Qian Xuesen Laboratory of Space Technology，Beijing 100094，China）

In the light of the agile satellite relative radiometric calibration method with all detectors of tilted linear CCD viewing the same scene，this paper provides the modeling and computation of satellite yaw angular velocity（YAV）based on the same trajectories of all detectors，which makes full use of the ability of yaw angle control.The space coordinate transform process from an object point on the earth to the image point in the focal plane is found.The formulas of geocentric angles are derived to be used for squint imaging mode.Furthermore，the calculation method of YAV for satellite CCD camera imaging the same scene is given.Taking an agile satellite equipped with 30，000 detectors in five CCD arrays and 0.3°tilted angle each other as an example，Simulation experiments are carried out，and the ground trajectory interval width is given during calibration process more than 30s imaging.Computation results indicate that YAV should be adjusted with certain interval period for all the detectors imaging the same scene.With YAV adjusting period of 0.36 s，the ground trajectory interval width is less than one pixel near the equator，and about six pixels at 50°latitude.This paper has important reference value for relative radiometriccalibration of the agile satellite based on all detectors imaging the same scene.

agile satellite；linear CCD camera；relative radiometric calibration；ground trajectory；yaw angular velocity（YAV）

TP722；V19

：ADOI：10.3969/j.issn.1673-8748.2015.05.007

2015-07-23；

：2015-08-30

李海超，男，博士，高級工程師，從事遙感衛星定標、遙感圖像處理等研究工作。Email：lihaichao2000@163. com。