反應(yīng)擴(kuò)散系統(tǒng)全局解的一致有界性和收斂性

張艷紅，劉永明

(1. 福州大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，福建 福州 350116;2. 華東師范大學(xué)數(shù)學(xué)系，上海 200062)

反應(yīng)擴(kuò)散系統(tǒng)全局解的一致有界性和收斂性

張艷紅1，劉永明2

(1. 福州大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院，福建 福州 350116;2. 華東師范大學(xué)數(shù)學(xué)系，上海 200062)

利用Gagliardo-Nirenberg不等式估計(jì)拋物型系統(tǒng)(P)的解不依賴時(shí)間的H1范數(shù)有界，從而得到系統(tǒng)的全局解及其一致有界性，最后得解的收斂性.

反應(yīng)擴(kuò)散; 全局解; 一致有界性; 收斂性

0 引言

考慮以下的拋物型系統(tǒng):

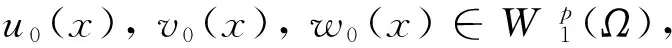
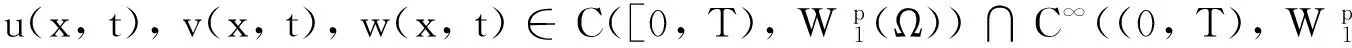
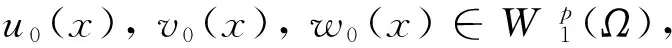
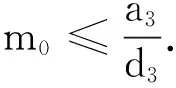
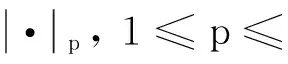
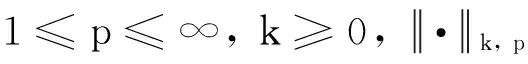
1 預(yù)備知識

引理1[2]若函數(shù)f∈H1([0,1]),則存在常數(shù)c>0,使得

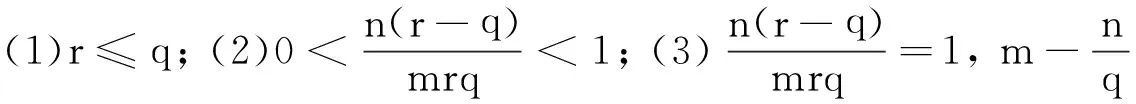
其中:

證明參見文[8]的定理10.1

推論1 若函數(shù)u∈H1([0,1]),則存在正常數(shù)c,c*,c**,使得

證明 取n=1,m=1,j=0,r=2,q=1,滿足定理2的條件(2),即得(3)和(4)式. 取n=1,m=1,j=0,r=2,q=2,滿足定理2的條件(1),即得(5)和(6)式.

注 由式(6)就有

引理2 對每一函數(shù)u∈H2([0,1]),且ux(0)=ux(1)=0,則有

對每一函數(shù)u∈H3([0,1]),且ux(0)=ux(1)=0,則有

證明 利用給定的邊界條件和H?lder不等式有

即得(8)式成立. 從(8)式有,

即得(9)式成立.

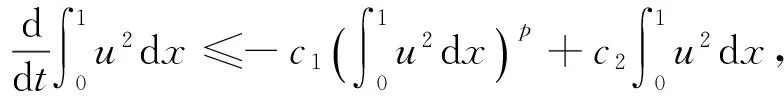
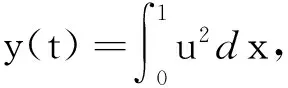
在不等式兩邊同乘以ec4t,再在(t0,t)上對兩邊同求積分得:

則

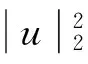
2 主要結(jié)果

2.1 全局解的存在性及其一致有界性

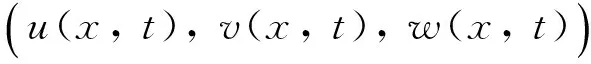
M=M(m0,Ei,ai,bi,ci,di,αij)>0

M*=M*(m0,Ei,ai,bi,ci,di,αij)>0 (i,j=1,2,3),(t>0)

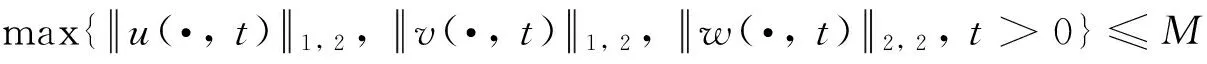
max{u(x,t),v(x,t),w(x,t):(x,t)∈[0,1]×(0,+∞)}≤M*

故對每一t>0有

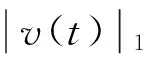
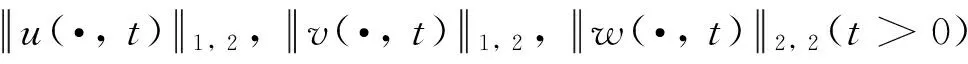
第一步 在(P)的第三式兩邊同乘以w,再在[0,1]上求積分得

故對每一t>0有

第二步 在(P)的第一式兩邊同乘以u,再在[0,1]上求積分得

由式(1),(10)得

所以

類似地,也有

在式(P)的第三式兩邊同乘以-wxx,再在[0,1]上求積分得

其中:

所以

式(12)+(13)+(14)得

對充分小的ε,由式(3)和(8)得

故對每一t>0 有

第三步在式(P)的第一式兩邊同乘以-uxx,再在[0,1]上求積分得

其中:

根據(jù)式(4)

所以,

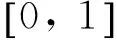
對式(P)的第三式求x的二階導(dǎo)數(shù),再兩邊同乘以wxx,而后在[0,1]上求積分得

其中:

所以,

由式(16)+(17)+(18)得

對充分小的ε,由式(8)和(9)得,

故對每一t>0,有

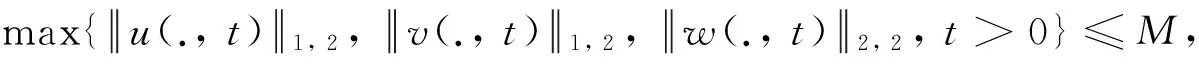
2.2 全局解的收斂性

定理4 設(shè)u0……