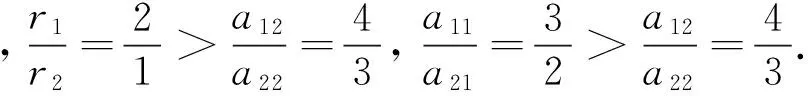一類反饋控制捕食-食餌系統平衡點的全局吸引
施春玲 ,王逸勤 ,陳育櫟
(1. 福州大學至誠學院,福建 福州 350002; 2. 福建教育學院,福建 福州 350002)
一類反饋控制捕食-食餌系統平衡點的全局吸引
施春玲1,王逸勤2,陳育櫟1
(1. 福州大學至誠學院,福建 福州 350002; 2. 福建教育學院,福建 福州 350002)
研究一類多時滯Lotka-Volterra捕食-食餌系統,通過構造多個Lyapunov函數,建立捕食-食餌系統正平衡點的全局吸引的充分性條件. 并進一步證明了當食餌種群絕滅,有其它食物來源的捕食者也能穩定在某個值.
捕食-食餌系統; 平衡點; 時滯; 全局吸引
1 引言及預備知識
考慮以下Lotka-Volterra捕食-食餌系統:
其中:x(t),y(t)分別表示食餌,捕食者在時刻t的種群密度;r1>0,r2>0分別表示食餌的內稟增長率和捕食者有其他食物來源的內稟生長率;aii>0,(i=1,2)表示種內作用系數;aij>0,(i≠j=1,2)表示種間作用系數,τ1>0,τ2>0分別表示追捕時間和捕食者的成熟期.
對于系統(1),當r2<0時,表示捕食者沒有其他食物,以食餌為唯一的食物來源,文獻[1]討論了正平衡點的穩定性及局部Holf分支,在此基礎上用等變拓撲理論建立一般的泛函微分方程的全局分支. 還有許多學者[2-7]對系統(1)或者其特殊形式解的持久性、周期性、或是Holf分支等做了大量工作. 但對系統(1)正平衡點和邊界平衡點穩定性的研究至今尚未見報道,于是我們假設τ=max{τ1,τ2},φ(θ),φ(θ)在[-τ,0]上是連續函數,系統(1)滿足初始條件
假設:
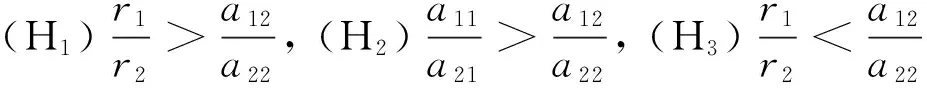
有以下引理:
引理1 若條件(H1)成立,容易得到系統(1)有唯一個正的平衡點(x*,y*),其中,
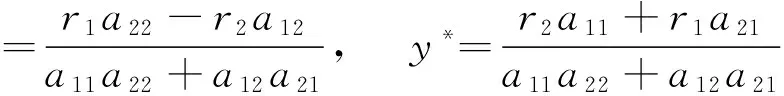

2 主要結論
定理1 若條件(H1)和(H2)成立,則系統(1)的唯一正平衡點(x*,y*)是全局漸近穩定的.
證明 作Lyapunov函數
所以由系統(1)得到,
所以
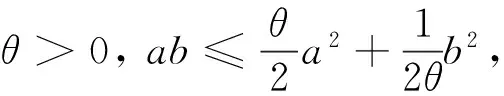
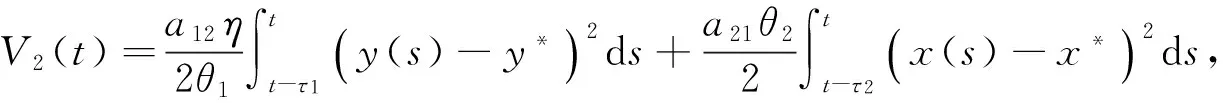
定義V(t)=V1(t)+V2(t). 由式(6)和(7)得:

所以從式(8)容易得到
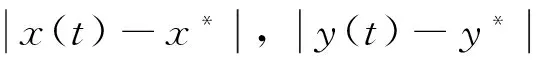
初始條件(2)和引理2意味著存在一個M>0,對所有的t∈R,0 所以V(T)有界. 因此由式(10)得知: 證明 條件(H3)成立,所以總存在常數α>0,β>0使得 所以存在常數ε>0,使得 令 兩邊同時求導 因此,由式(13)、(14)和a11α+βa21>0 ,得到W′(t)≤-εW(t).從0 到t進行積分,得到 同定理1的證明,存在M>0使得0 另一方面, 綜合式(15)和(17),可以得到 M-βexp(-βa21Mτ2-αa12Mτ1)xα(t)≤W(t)≤W(0)exp(-εt) 所以 xα(t)≤Mβexp(βa21Mτ2+αa12Mτ1)W(0)exp(-εt) 即 所以 與定理1的證明類似,存在M>0使得0 定義M(t)=M1(t)+M2(t). 由式(20)和(21)得: 從T→t對式(22)兩邊同時積分, 例1 考慮以下時滯的捕食-食餌系統 例2……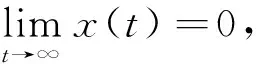
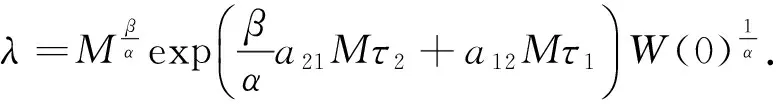
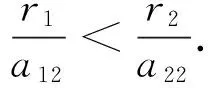
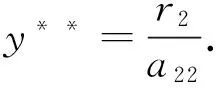
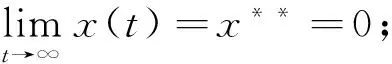
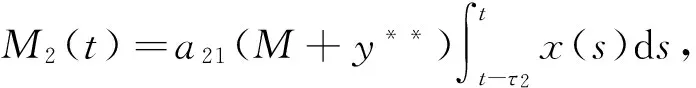
3 數值模擬